9.2: Série Infinite
- Page ID
- 188365
- Explique o significado da soma de uma série infinita.
- Calcule a soma de uma série geométrica.
- Avalie uma série telescópica.
Vimos que uma sequência é um conjunto ordenado de termos. Se você adicionar esses termos juntos, obterá uma série. Nesta seção, definimos uma série infinita e mostramos como as séries estão relacionadas às sequências. Também definimos o que significa para uma série convergir ou divergir. Apresentamos um dos tipos mais importantes de séries: a série geométrica. Usaremos séries geométricas no próximo capítulo para escrever certas funções como polinômios com um número infinito de termos. Esse processo é importante porque nos permite avaliar, diferenciar e integrar funções complicadas usando polinômios mais fáceis de manusear. Também discutimos a série harmônica, sem dúvida a série divergente mais interessante porque ela simplesmente não consegue convergir.
Somas e séries
Uma série infinita é uma soma de infinitos termos e é escrita na forma
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯.\)
Mas o que isso significa? Não podemos adicionar um número infinito de termos da mesma forma que podemos adicionar um número finito de termos. Em vez disso, o valor de uma série infinita é definido em termos do limite de somas parciais. A soma parcial de uma série infinita é uma soma finita da forma
\(\displaystyle \sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k.\)
Para ver como usamos somas parciais para calcular séries infinitas, considere o exemplo a seguir. Suponha que o óleo esteja se infiltrando em um lago, de forma que\( 1000\) galões entrem no lago na primeira semana. Durante a segunda semana, mais\( 500\) galões de óleo entram no lago. Na terceira semana,\( 250\) mais galões entram no lago. Suponha que esse padrão continue de forma que a cada semana metade do óleo entre no lago do que na semana anterior. Se isso continuar para sempre, o que podemos dizer sobre a quantidade de óleo no lago? A quantidade de óleo continuará a ficar arbitrariamente grande ou é possível que ela se aproxime de uma quantidade finita? Para responder a essa pergunta, analisamos a quantidade de óleo no lago após\( k\) semanas. Deixando\( S_k\) indicar a quantidade de óleo no lago (medida em milhares de galões) após\( k\) semanas, vemos que
\( S_1=1\)
\( S_2=1+0.5=1+\frac{1}{2}\)
\( S_3=1+0.5+0.25=1+\frac{1}{2}+\frac{1}{4}\)
\( S_4=1+0.5+0.25+0.125=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\)
\( S_5=1+0.5+0.25+0.125+0.0625=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}.\)
Observando esse padrão, vemos que a quantidade de óleo no lago (em milhares de galões) após\( k\) semanas é
\[ S_k=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯+\frac{1}{2^{k−1}}=\sum_{n=1}^k\left(\frac{1}{2}\right)^{n−1}. \nonumber \]
Estamos interessados no que acontece, como\( k→∞.\) simbolicamente, a quantidade de óleo no lago, conforme\( k→∞\) é dada pela série infinita.
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯. \nonumber \]
Ao mesmo tempo\( k→∞\), a quantidade de óleo no lago pode ser calculada avaliando\(\displaystyle \lim_{k→∞}S_k\). Portanto, o comportamento da série infinita pode ser determinado observando o comportamento da sequência de somas parciais\( {S_k}\). Se a sequência de somas parciais\( {S_k}\) convergir, dizemos que a série infinita converge e sua soma é dada por\(\displaystyle \lim_{k→∞}S_k\). Se a sequência\( {S_k}\) divergir, dizemos que a série infinita diverge. Agora voltamos nossa atenção para determinar o limite dessa sequência\( {S_k}\).
Primeiro, simplificando algumas dessas somas parciais, vemos que
\( S_1=1\)
\( S_2=1+\frac{1}{2}=\frac{3}{2}\)
\( S_3=1+\frac{1}{2}+\frac{1}{4}=\frac{7}{4}\)
\( S_4=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{15}{8}\)
\( S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.\)
Traçando alguns desses valores na Figura, parece que a sequência\( {S_k}\) pode estar se aproximando de 2.
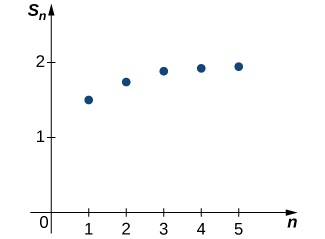
Vamos procurar evidências mais convincentes. Na tabela a seguir, listamos os valores de\(S_k\) para vários valores de\(k\).
| \( k\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \( S_k\) | 1.9375 | 1.998 | 1,999939 | 1,999998 |
Esses dados fornecem mais evidências sugerindo que a sequência\({S_k}\) converge para\(2\). Posteriormente, forneceremos um argumento analítico que pode ser usado para provar isso\(\displaystyle \lim_{k→∞}S_k=2\). Por enquanto, contamos com os dados numéricos e gráficos para nos convencermos de que a sequência de somas parciais realmente converge para\(2\). Como essa sequência de somas parciais converge para\(2\), dizemos que a série infinita converge\(2\) e escreve
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber \]
Voltando à pergunta sobre o óleo no lago, uma vez que essa série infinita converge para\(2\), concluímos que a quantidade de óleo no lago se aproximará arbitrariamente de\(2000\) galões à medida que a quantidade de tempo se tornar suficientemente grande.
Esta série é um exemplo de uma série geométrica. Discutiremos as séries geométricas com mais detalhes posteriormente nesta seção. Primeiro, resumimos o que significa convergir uma série infinita.
Uma série infinita é uma expressão da forma
\[\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber \]
Para cada número inteiro positivo\(k\), a soma
\[S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber \]
é chamada de soma\(k^{\text{th}}\) parcial da série infinita. As somas parciais formam uma sequência\({S_k}\). Se a sequência de somas parciais convergir para um número real\(S\), a série infinita converge. Se pudermos descrever a convergência de uma série para\(S\), chamamos\(S\) a soma da série e escrevemos
\[\sum_{n=1}^∞a_n=S. \nonumber \]
Se a sequência de somas parciais divergir, temos a divergência de uma série.
Observe que o índice de uma série não precisa começar com\(n=1\), mas pode começar com qualquer valor. Por exemplo, a série
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber \]
também pode ser escrito como
\[\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber \]
Muitas vezes, é conveniente que o índice comece em\(1\), então, se por algum motivo ele começar com um valor diferente, podemos reindexar fazendo uma alteração nas variáveis. Por exemplo, considere a série
\[ \sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]
Ao introduzir a variável\(m=n−1\), para que\(n=m+1,\) possamos reescrever a série como
\[ \sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber \]
Para cada uma das séries a seguir, use a sequência de somas parciais para determinar se a série converge ou diverge.
- \(\displaystyle \sum_{n=1}^∞\frac{n}{n+1}\)
- \(\displaystyle \sum_{n=1}^∞(−1)^n\)
- \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}\)
Solução
a. A sequência de somas parciais\({S_k}\) satisfaz
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}\).
Observe que cada termo adicionado é maior que\(1/2\). Como resultado, vemos que
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).\)
A partir desse padrão, podemos ver isso\(S_k>k\left(\frac{1}{2}\right)\) para cada número inteiro\(k\). Portanto,\({S_k}\) é ilimitado e, consequentemente, diverge. Portanto, a série infinita\(\displaystyle \sum^∞_{n=1}\frac{n}{n+1}\) diverge.
b. A sequência de somas parciais\({S_k}\) satisfaz
\(S_1=−1\)
\(S_2=−1+1=0\)
\(S_3=−1+1−1=−1\)
\(S_4=−1+1−1+1=0.\)
A partir desse padrão, podemos ver que a sequência de somas parciais é
\[{S_k}={−1,0,−1,0,…}. \nonumber \]
Como essa sequência diverge, a série infinita\(\displaystyle \sum^∞_{n=1}(−1)^n\) diverge.
c. A sequência de somas parciais\( {S_k}\) satisfaz
\( S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}\)
\( S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\)
\( S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}\)
\( S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}\)
\( S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.\)
A partir desse padrão, podemos ver que a soma\( k^{\text{th}}\) parcial é dada pela fórmula explícita
\[ S_k=\frac{k}{k+1} \nonumber \].
\( k/(k+1)→1,\)Pois concluímos que a sequência de somas parciais converge e, portanto, a série infinita converge para\( 1\). Nós temos
\[ \sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber \]
Determine se a série\(\displaystyle \sum^∞_{n=1}\frac{n+1}{n}\) converge ou diverge.
- Dica
-
Veja a sequência de somas parciais.
- Resposta
-
A série diverge por causa da soma\( k^{\text{th}}\) parcial\( S_k>k\).
A série Harmonic
Uma série útil que você deve conhecer é a série harmônica. A série harmônica é definida como
\[\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber \]
Essa série é interessante porque diverge, mas diverge muito lentamente. Com isso, queremos dizer que os termos na sequência de somas parciais\( {S_k}\) se aproximam do infinito, mas o fazem muito lentamente. Mostraremos que a série diverge, mas primeiro ilustramos o lento crescimento dos termos na sequência\( {S_k}\) na tabela a seguir.
| \( k\) | 10 | 100 | 1000 | 10,00 | 100.000 | 1.000.000 |
|---|---|---|---|---|---|---|
| \( S_k\) | 2.92897 | 5.18738 | 7.48547 | 9.78761 | 12.09015 | 14.39273 |
Mesmo depois dos\( 1,000,000\) termos, a soma parcial ainda é relativamente pequena. A partir dessa tabela, não está claro se essa série realmente diverge. No entanto, podemos mostrar analiticamente que a sequência de somas parciais diverge e, portanto, a série diverge.
Para mostrar que a sequência de somas parciais diverge, mostramos que a sequência de somas parciais é ilimitada. Começamos escrevendo as primeiras somas parciais:
\( S_1=1\)
\( S_2=1+\dfrac{1}{2}\)
\( S_3=1+\dfrac{1}{2}+\dfrac{1}{3}\)
\( S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\).
Observe que, nos dois últimos termos em\( S_4\),
\[ \frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber \]
Portanto, concluímos que
\[ S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber \]
Usando a mesma ideia para\( S_8\), vemos que
\(\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right)\).
A partir desse padrão, vemos isso\( S_1=1, S_2=1+1/2, S_4>1+2(1/2),\)\( S_8>1+3(1/2)\) e. De forma mais geral, pode-se demonstrar isso\( S_{2^j}>1+j(1/2)\) para todos\( j>1\). Uma vez que\( 1+j(1/2)→∞,\) concluímos que a sequência\( {S_k}\) é ilimitada e, portanto, diverge. Na seção anterior, afirmamos que as sequências convergentes são limitadas. Consequentemente, uma vez que\( {S_k}\) é ilimitado, ele diverge. Assim, a série harmônica diverge.
Propriedades algébricas de séries convergentes
Como a soma de uma série infinita convergente é definida como um limite de uma sequência, as propriedades algébricas das séries listadas abaixo seguem diretamente das propriedades algébricas das sequências.
\(\displaystyle \sum_{n=1}^∞ b_n\)Seja uma série convergente.\(\displaystyle \sum_{n=1}^∞ a_n\) Então, as seguintes propriedades algébricas são válidas.
i. A série\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) converge e\(\displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n.\) (regra de soma)
ii. A série\(\displaystyle \sum_{n=1}^∞(a_n−b_n)\) converge e\(\displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n.\) (regra da diferença)
iii. Para qualquer número real\( c\), a série\(\displaystyle \sum_{n=1}^∞ca_n\) converge,\(\displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n\) e. (Regra múltipla constante)
Avalie\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].\)
Solução
Mostramos anteriormente que
\[ \sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber \]
e
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber \]
Como ambas as séries convergem, podemos aplicar as propriedades do Note\(\PageIndex{1}\) para avaliar
\[\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber \]
Usando a regra da soma, escreva
\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.\)
Então, usando a regra do múltiplo constante e as somas acima, podemos concluir que
\(\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.\)
Avalie\(\displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}\).
- Dica
-
Reescreva como\(\displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}\).
- Resposta
-
10
Série geométrica
Uma série geométrica é qualquer série que podemos escrever na forma
\[ a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber \]
Como a razão entre cada termo desta série e o termo anterior é r, o número r é chamado de razão. Nós nos referimos a como o termo inicial porque é o primeiro termo da série. Por exemplo, a série
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber \]
é uma série geométrica com termo\( a=1\) e proporção iniciais\( r=1/2\).
Em geral, quando uma série geométrica converge? Considere a série geométrica
\[\sum_{n=1}^∞ar^{n−1} \nonumber \]
quando\( a>0\). Sua sequência de somas parciais\( {S_k}\) é dada por
\[S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber \]
Considere o caso quando,\( r=1.\) nesse caso,
\[S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber \]
Desde então\( a>0\), nós conhecemos\( ak→∞\) como\( k→∞\). Portanto, a sequência de somas parciais é ilimitada e, portanto, diverge. Consequentemente, a série infinita diverge para\( r=1\). Para\( r≠1\), para encontrar o limite de\( {S_k}\), multiplique Equação por\( 1−r\). Fazendo isso, vemos que
\[ (1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber \]
Todos os outros termos são cancelados.
Portanto,
\( S_k=\dfrac{a(1−r^k)}{1−r}\)para\( r≠1\).
De nossa discussão na seção anterior, sabemos que a sequência geométrica\( r^k→0\) se\( |r|<1\) e aquela\( r^k\) diverge se\( |r|>1\) ou\( r=±1\). Portanto, para\( |r|<1, S_k→\dfrac{a}{1−r}\) e nós temos
\[ \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber \]
Se\( |r|≥1, S_k\) diverge e, portanto,
\[ \sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber \]
Uma série geométrica é uma série da forma
\[\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \nonumber \]
Se\( |r|<1\), a série converge, e
\[\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber \]
Se sim\( |r|≥1\), a série diverge.
As séries geométricas às vezes aparecem em formas ligeiramente diferentes. Por exemplo, às vezes o índice começa com um valor diferente de\( n=1\) ou o expoente envolve uma expressão linear para\( n\) diferente de\( n−1\). Desde que possamos reescrever a série na forma dada pela Equação, ela é uma série geométrica. Por exemplo, considere a série
\[\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber \]
Para ver que esta é uma série geométrica, escrevemos os primeiros termos:
\(\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.\)
Vemos que o termo inicial é\( a=4/9\) e a proporção é\( r=2/3.\) Portanto, a série pode ser escrita como
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.\)
Uma vez que\( r=2/3<1\), essa série converge e sua soma é dada por
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.\)
Determine se cada uma das seguintes séries geométricas converge ou diverge e, se ela converge, encontre sua soma.
- \(\displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}\)
- \(\displaystyle \sum^∞_{n=1}e^{2n}\)
Solução
a. Escrevendo os primeiros termos da série, temos
\[\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}\]
O termo inicial\( a=−3\) e a proporção\( r=−3/4\). Desde então\( |r|=3/4<1\), a série converge para
\[ \frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber \]
b. Escrevendo esta série como
\[ e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber \]
podemos ver que esta é uma série geométrica onde,\( r=e^2>1.\) portanto, a série diverge.
Determine se a série\(\displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1}\) converge ou diverge. Se convergir, encontre sua soma.
- Dica
-
\( r=−2/5\)
- Resposta
-
\( 5/7\)
Agora voltamos nossa atenção para uma boa aplicação de séries geométricas. Mostramos como eles podem ser usados para escrever decimais repetidos como frações de números inteiros.
Use uma série geométrica para escrever\( 3.\bar{26}\) como uma fração de números inteiros.
Solução
Desde a\( 3.\bar{26}—=3.262626…,\) primeira vez que escrevemos
\[\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{1000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}\]
Ignorando o termo 3, o resto dessa expressão é uma série geométrica com termo\( a=26/10^2\) e proporção iniciais.\( r=1/10^2.\) Portanto, a soma dessa série é
\[ \frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber \]
Assim,
\( 3.262626…=3+\frac{26}{99}=\frac{323}{99}\).
Escreva\( 5.2\bar{7}\) como uma fração de números inteiros.
- Dica
-
Ao expressar esse número como uma série, encontre uma série geométrica com termo\( a=7/100\) e proporção iniciais\( r=1/10\).
- Resposta
-
\( 475/90\)
Defina uma sequência de figuras\( \{F_n\}\) recursivamente da seguinte forma (Figura\(\PageIndex{2}\)). \( F_0\)Seja um triângulo equilátero com lados de comprimento\( 1\). Pois\( n≥1\),\( F_n\) seja a curva criada removendo o terço médio de cada lado\( F_{n−1}\) e substituindo-o por um triângulo equilátero apontando para fora. O número limite, conhecido como\( n→∞\) floco de neve de Koch.
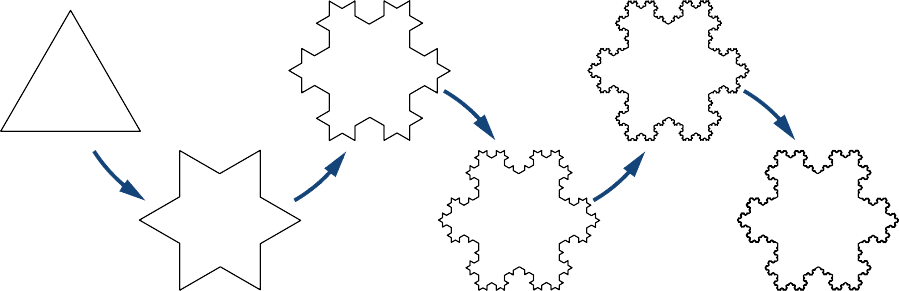
- Encontre o comprimento\( L_n\) do perímetro de\( F_n\). Avalie\(\displaystyle \lim_{n→∞}L_n\) para encontrar o comprimento do perímetro do floco de neve de Koch.
- Encontre a área\( A_n\) da figura\( F_n\). Avalie\(\displaystyle \lim_{n→∞}A_n\) para encontrar a área do floco de neve de Koch.
Solução
a. Vamos\( N_n\) indicar o número de lados da figura\( F_n\). Uma vez que\( F_0\) é um triângulo,\( N_0=3\). Vamos indicar o comprimento de cada lado do\( F_n\). Como\( F_0\) é um triângulo equilátero com lados de comprimento\( l_0=1\), agora precisamos determinar\( N_1\)\( l_1\) e. Como\( F_1\) é criado removendo o terço médio de cada lado e substituindo esse segmento de linha por dois segmentos de linha, para cada lado\( F_0\), obtemos quatro lados\( F_1\). Portanto, o número de lados para\( F_1\) é
\( N_1=4⋅3\).
Como o comprimento de cada um desses novos segmentos de linha é\( 1/3\) o comprimento dos segmentos de linha em\( F_0\), o comprimento dos segmentos de linha para\( F_1\) é dado por
\( l_1=\frac{1}{3}⋅1=\frac{1}{3}\).
Da mesma forma\( F_2\), pois, uma vez que o terço médio de cada lado de\( F_1\) é removido e substituído por dois segmentos de linha, o número de lados em\( F_2\) é dado por
\( N_2=4N_1=4(4⋅3)=4^2⋅3.\)
Como o comprimento de cada um desses lados é\( 1/3\) o comprimento dos lados de\( F_1\), o comprimento de cada lado da figura\( F_2\) é dado por
\( l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2\).
De forma mais geral, uma vez que\( F_n\) é criado removendo o terço médio de cada lado\( F_{n−1}\) e substituindo esse segmento de linha por dois segmentos de linha de comprimento\( \frac{1}{3}l_{n−1}\) na forma de um triângulo equilátero, sabemos que\( N_n=4N_{n−1}\)\( l_n=\dfrac{l_{n−1}}{3}\) e. Portanto, o número de lados da figura\( F_n\) é
\( N_n=4^n⋅3\)
e o comprimento de cada lado é
\[ l_n=\left(\frac{1}{3}\right)^n. \nonumber \]
Portanto, para calcular o perímetro de\( F_n\), multiplicamos o número de lados\( N_n\) e o comprimento de cada lado\( l_n\). Concluímos que o perímetro de\( F_n\) é dado por
\[ L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber \]
Portanto, o comprimento do perímetro do floco de neve de Koch é
\[ L=\lim_{n→∞}L_n=∞. \nonumber \]
b. Vamos\( T_n\) indicar a área de cada novo triângulo criado durante a formação\( F_n\). Para\( n=0, T_0\) é a área do triângulo equilátero original. Portanto,\( T_0=A_0=\sqrt{3}/4\). Pois\( n≥1\), como os comprimentos dos lados do novo triângulo são\( 1/3\) o comprimento dos lados de\( F_{n−1}\), temos
\[ T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber \]
Portanto,\( T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}\). Como um novo triângulo é formado em cada lado do\( F_{n−1}\),
\[ A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber \]
Escrevendo os primeiros termos\( A_0,A_1,A_2,\), vemos que
\( A_0=\frac{\sqrt{3}}{4}\)
\(A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]\)
\( A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2]\).
De forma mais geral,
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right]\).
Considerando cada\( 4/9\) termo dentro dos parênteses internos, reescrevemos nossa expressão como
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right]\).
A expressão\( 1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\) é uma soma geométrica. Conforme mostrado anteriormente, essa soma satisfaz
\( 1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.\)
Substituindo essa expressão pela expressão acima e simplificando, concluímos que
\[ A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber \]
Portanto, a área do floco de neve de Koch é
\(\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.\)
Análise
O floco de neve de Koch é interessante porque tem área finita, mas perímetro infinito. Embora à primeira vista isso possa parecer impossível, lembre-se de que você viu exemplos semelhantes anteriormente no texto. Por exemplo, considere a região delimitada pela curva\( y=1/x^2\) e o\( x\) eixo -no intervalo\( [1,∞).\) Desde a integral imprópria
\[ ∫^∞_1\frac{1}{x^2}\,dx \nonumber \]
converge, a área dessa região é finita, mesmo que o perímetro seja infinito.
Série Telescoping
Considere a série.\(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\) Discutimos esta série em Exemplo, mostrando que a série converge escrevendo as primeiras somas parciais\( S_1,S_2,…,S_6\) e percebendo que elas são todas da forma\( S_k=\dfrac{k}{k+1}\). Aqui usamos uma técnica diferente para mostrar que essa série converge. Usando frações parciais, podemos escrever
\[ \frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber \]
Portanto, a série pode ser escrita como
\(\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1+\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.\)
Escrevendo os primeiros vários termos na sequência de somas parciais,\( {S_k},\) vemos que
\( S_1=1−\frac{1}{2}\)
\( S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}\)
\( S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}\).
Em geral,
\( S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}\).
Percebemos que os termos intermediários se cancelam, deixando apenas o primeiro e o último período. Em certo sentido, a série colapsa como uma luneta com tubos que desaparecem um no outro para encurtar o telescópio. Por esse motivo, chamamos uma série que tem essa propriedade de série telescópica. Para esta série, desde\( S_k=1−1/(k+1)\) e\( 1/(k+1)→0\) como\( k→∞\), a sequência de somas parciais converge para e\( 1\), portanto, a série converge para\( 1\).
Uma série telescópica é uma série na qual a maioria dos termos se cancela em cada uma das somas parciais, restando apenas alguns dos primeiros termos e alguns dos últimos termos.
Por exemplo, qualquer série do formulário
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯\)
é uma série telescópica. Podemos ver isso escrevendo algumas das somas parciais. Em particular, vemos que
\( S_1=b_1−b_2\)
\( S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3\)
\( S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.\)
Em geral, a késima soma parcial desta série é
\( S_k=b_1−b_{k+1}\).
Como a késima soma parcial pode ser simplificada para a diferença desses dois termos, a sequência de somas parciais\( {S_k}\) convergirá se e somente se a sequência\( {b_{k+1}}\) convergir. Além disso, se a sequência\( b_{k+1}\) convergir para algum número finito B, a sequência de somas parciais converge para e\( b_1−B\), portanto,
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.\)
No próximo exemplo, mostramos como usar essas ideias para analisar uma série telescópica dessa forma.
Determine se a série telescópica
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]\)
converge ou diverge. Se convergir, encontre sua soma.
Solução
Ao escrever termos na sequência de somas parciais, podemos ver que
\( S_1=\cos(1)−\cos(\frac{1}{2})\)
\( S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})\)
\( S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))\)
\( =\cos(1)−\cos(\frac{1}{4})\).
Em geral,
\( S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right)\).
\( 1/(k+1)→0\)Como\( k→∞\) e\( \cos x\) é uma função contínua,\( \cos(1/(k+1))→\cos(0)=1\). Portanto, concluímos que\( S_k→\cos(1)−1\). A série telescópica converge e a soma é dada por
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.\)
Determine se\(\displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}]\) converge ou diverge. Se convergir, encontre sua soma.
- Dica
-
Escreva a sequência de somas parciais para ver quais termos são cancelados.
- Resposta
-
\( e−1\)
Mostramos que a série harmônica\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge. Aqui, investigamos o comportamento das somas parciais,\( S_k\) pois,\( k→∞.\) em particular, mostramos que elas se comportam como a função logarítmica natural, mostrando que existe uma constante\( γ\) como
\(\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ\)como\( k→∞.\)
Essa constante\( γ\) é conhecida como constante de Euler.
1. Vamos\(\displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right).\) avaliar\( T_k\) vários valores de\( k\).
2. Para\( T_k\), conforme definido na parte 1. mostre que a sequência\( {T_k}\) converge usando as etapas a seguir.
a. Mostre que a sequência\( {T_k}\) é monótona diminuindo. (Dica: mostre que\( \ln(1+1/k>1/(k+1))\)
b. Mostre que a sequência\( {T_k}\) está limitada abaixo por zero. (Dica:\( \ln k\) Expresse como uma integral definida.)
c. Use o Teorema da Convergência Monótona para concluir que a sequência\( {T_k}\) converge. O limite\( γ\) é a constante de Euler.
3. Agora, estime\( T_k\) a distância\( γ\) de um determinado número inteiro\( k\). Prove isso\( k≥1, 0<T_k−γ≤1/k\) usando as etapas a seguir.
a. Mostre que\( \ln(k+1)−\ln k<1/k.\)
b. Use o resultado da parte a. para mostrar que, para qualquer número inteiro\( k\),
\[ T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber \]
c. Para qualquer número inteiro\( k\) e\( j\) tal que\( j>k\), expresse\( T_k−T_j\) como uma soma telescópica escrevendo
\[ T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber \]
Use o resultado da parte b. combinado com essa soma telescópica para concluir que
\[ T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber \]
a. Aplique o limite em ambos os lados da desigualdade na parte c. para concluir que
\[ T_k−γ≤\frac{1}{k}. \nonumber \]
e. Faça uma estimativa\( γ\) com uma precisão dentro de 0,001.
Conceitos chave
- Dada a série infinita
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯\)
e a sequência correspondente de somas parciais\( {S_k}\) onde
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\),
a série converge se e somente se a sequência\( {S_k}\) convergir.
- A série geométrica\(\displaystyle \sum^∞_{n=1}ar^{n−1}\) converge se\( |r|<1\) e diverge se\( |r|≥1.\) For\( |r|<1,\)
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\).
- A série harmônica
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
diverge.
- Uma série da forma\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯\) é uma série telescópica. A soma\( k^{\text{th}}\) parcial desta série é dada por\( S_k=b_1−b_{k+1}\). A série convergirá se e somente se\(\displaystyle \lim_{k→∞} b_{k+1}\) existir. Nesse caso,
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1})\).
Equações chave
- Série harmônica
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)
- Soma de uma série geométrica
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\)para\( |r|<1\)
Glossário
- convergência de uma série
- uma série converge se a sequência de somas parciais dessa série convergir
- divergência de uma série
- uma série diverge se a sequência de somas parciais dessa série divergir
- série geométrica
- uma série geométrica é uma série que pode ser escrita na forma
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯\)
- série harmônica
- a série harmônica assume a forma
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
- série infinita
- uma série infinita é uma expressão da forma
\(\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n\)
- soma parcial
-
a soma\( kth\) parcial da série infinita\(\displaystyle \sum^∞_{n=1}a_n\) é a soma finita
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\)
- série telescópica
- uma série telescópica é aquela em que a maioria dos termos se cancela em cada uma das somas parciais


