9.2E: Exercícios para a Seção 9.2

Last updated
Save as PDF

Page ID: 188378

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, use a notação sigma para escrever cada expressão como uma série infinita.

1)$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯$

Resposta: $\displaystyle \sum_{n=1}^∞\frac{1}{n}$

2)$ 1−1+1−1+⋯$

3)$ 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...$

Resposta: $\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}$

4)$ \sin 1+\sin \frac{1}{2}+\sin \frac{1}{3}+\sin \frac{1}{4}+⋯$

Nos exercícios 5 a 8, calcule as primeiras quatro somas parciais$ S_1,…,S_4$ para a série cujo$ n^{\text{th}}$ período$ a_n$ começa com a$ n=1$ seguinte.

5)$ a_n=n$

Resposta: $ 1,3,6,10$

6)$ a_n=1/n$

7)$ a_n=\sin \frac{nπ}{2}$

Resposta: $ 1,1,0,0$

8)$ a_n=(−1)^n$

Nos exercícios 9 a 12, calcule o termo geral$ a_n$ da série com a soma parcial dada$ S_n$. Se a sequência de somas parciais convergir, encontre seu limite$ S$.

9)$ S_n=1−\frac{1}{n}, \quad n≥2$

Resposta: $ a_n=S_n−S_{n−1}=\dfrac{1}{n−1}−\dfrac{1}{n}.$Uma vez que$\displaystyle S = \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left(1−\frac{1}{n}\right) = 1,$ a série converge para$ S=1.$

10)$ S_n=\dfrac{n(n+1)}{2}, \quad n≥1$

11)$ S_n=\sqrt{n},\quad n≥2$

Resposta: $ a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\dfrac{1}{\sqrt{n−1}+\sqrt{n}}.$
A série diverge porque as somas parciais são ilimitadas.
Ou seja,$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \sqrt{n} = \infty.$

12)$ S_n=2−\dfrac{n+2}{2^n},\quad n≥1$

Para cada série nos exercícios 13 a 16, use a sequência de somas parciais para determinar se a série converge ou diverge.

13)$\displaystyle \sum_{n=1}^∞\frac{n}{n+2}$

Resposta: $ S_1=1/3,$
$ S_2=1/3+2/4>1/3+1/3=2/3,$
$S_3=1/3+2/4+3/5>3⋅(1/3)=1.$
Em geral$ S_k>k/3,$, a série diverge.
Observe que o$n^{\text{th}}$ Term Test for Divergence também pode ser usado para provar que esta série diverge.

14)$\displaystyle \sum_{n=1}^∞(1−(−1)^n))$

15)$\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}$$\quad\Big($ Dica: Use uma decomposição parcial de frações como essa para$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\Big)$

Resposta

$ S_1=1/(2\cdot 3)=1/6=2/3−1/2,$

$ S_2=1/(2\cdot 3)+1/(3\cdot 4)=2/12+1/12=1/4=3/4−1/2,$

$ S_3=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)=10/60+5/60+3/60=3/10=4/5−1/2,$

$ S_4=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)+1/(5\cdot 6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.$

O padrão é$ S_k=\dfrac{k+1}{k+2}−\dfrac{1}{2}.$
Então,$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left( \dfrac{k+1}{k+2}−\dfrac{1}{2} \right) = \dfrac{1}{2},$ então a série converge para$ 1/2.$

16)$\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}$$\quad\Big($ Dica: Siga o raciocínio para$\displaystyle \sum_{n=1}^∞\frac{1}{n}.\Big)$

Suponha isso$\displaystyle \sum_{n=1}^∞a_n=1$$\displaystyle \sum_{n=1}^∞b_n=−1$, isso$ a_1=2$, aquilo,$ b_1=−3$ e. Use essas informações para encontrar a soma das séries indicadas nos exercícios 17 a 20.

17)$\displaystyle \sum_{n=1}^∞(a_n+b_n)$

Resposta: $ \displaystyle \sum_{n=1}^∞(a_n+b_n) \quad = \quad \sum_{n=1}^∞ a_n + \sum_{n=1}^∞ b_n \quad = \quad 1 + (-1) \quad = \quad 0$

18)$\displaystyle \sum_{n=1}^∞(a_n−2b_n)$

19)$\displaystyle \sum_{n=2}^∞(a_n−b_n)$

Resposta: $\displaystyle \sum_{n=2}^∞(a_n−b_n) \quad = \quad \sum_{n=2}^∞ a_n - \sum_{n=2}^∞ b_n \quad = \quad \left(\sum_{n=1}^∞ a_n - a_1\right) - \left(\sum_{n=1}^∞ b_n -b_1\right) \quad = \quad (1 - 2) - (-1 - (-3)) = -1 - 2 \quad = \quad -3$

20)$\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})$

Nos exercícios 21 a 26, indique se a série dada converge ou diverge e explique o porquê.

21)$\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}$ (Dica: reescreva usando uma mudança de índice.)

Resposta: A série diverge,$\displaystyle \sum_{n=1001}^∞\frac{1}{n}$

22)$\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}$ (Dica: reescreva usando uma mudança de índice.)

23)$ 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯$

Resposta: Esta é uma série geométrica convergente, já que$ r=\frac{1}{10}<1$

24)$ 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯$

25)$ 1+\frac{π}{e^2}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯$

Resposta: Esta é uma série geométrica convergente, já que$ r=π/e^2<1$

26)$ 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯$

Para cada um$ a_n$ dos exercícios 27 a 30, escreva sua soma como uma série geométrica do formulário$\displaystyle \sum_{n=1}^∞ar^n$. Indique se a série converge e, em caso afirmativo, encontre o valor exato de sua soma.

27)$ a_1=−1$ e$ \dfrac{a_n}{a_{n+1}}=−5$ para$ n≥1.$

Resposta: $\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n$, converge para$ −5/6$

28)$ a_1=2$ e$ \dfrac{a_n}{a_{n+1}}=1/2$ para$ n≥1.$

29)$ a_1=10$ e$ \dfrac{a_n}{a_{n+1}}=10$ para$ n≥1$.

Resposta: $\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,$converge para$\frac{100}{9}$

30)$ a_1=\frac{1}{10}$ e$ a_n/a_{n+1}=−10$ para$ n≥1$.

Nos exercícios 31 a 34, use a identidade$\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n$ (que é verdadeira para$|y| < 1$) para expressar cada função como uma série geométrica no termo indicado.

31)$ \dfrac{x}{1+x}$ em$ x$

Resposta: $\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n$

32)$ \dfrac{\sqrt{x}}{1−x^{3/2}}$ em$ \sqrt{x}$

33)$ \dfrac{1}{1+\sin^2x}$ em$\sin x$

Resposta: $\displaystyle \sum_{n=0}^∞(−1)^n\sin^{2n}(x)$

34)$ \sec^2 x$ em$\sin x$

Nos exercícios 35 a 38, avalie a série telescópica ou indique se a série diverge.

(35)$\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}$

Resposta: $ S_k=2−2^{1/(k+1)}→1$como$ k→∞.$

36)$\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}$

37)$\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})$

Resposta: $ S_k=1−\sqrt{k+1}$diverge

38)$\displaystyle \sum_{n=1}^∞(\sin n−\sin(n+1))$

Expresse cada série nos exercícios 39 a 42 como uma soma telescópica e avalie sua soma$n^{\text{th}}$ parcial.

39)$\displaystyle \sum_{n=1}^∞\ln\left(\frac{n}{n+1}\right)$

Resposta: $\displaystyle \sum_{n=1}^∞[\ln n−\ln(n+1)],$
$S_k=−\ln(k+1)$

40)$\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}$ (Dica: fatore o denominador e use frações parciais.)

41)$\displaystyle \sum_{n=2}^∞\frac{\ln\left(1+\frac{1}{n}\right)}{(\ln n)\ln(n+1)}$

Resposta: $ a_n=\frac{1}{\ln n}−\frac{1}{\ln(n+1)}$e$ S_k=\frac{1}{\ln(2)}−\frac{1}{\ln(k+1)}→\frac{1}{\ln(2)}$

42)$\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}$ (Dica: Veja$ 1/(n2^n)$.

Uma série geral de telescópios é aquela em que todos, exceto os primeiros termos, se cancelam após a soma de um determinado número de termos sucessivos.

43) Deixe$ a_n=f(n)−2f(n+1)+f(n+2),$ entrar$ f(n)→0$ como$ n→∞.$ Find$\displaystyle \sum_{n=1}^∞a_n$.

Resposta: $\displaystyle \sum_{n=1}^∞a_n=f(1)−f(2)$

44)$ a_n=f(n)−f(n+1)−f(n+2)+f(n+3),$ em que$ f(n)→0$ como$ n→∞$. Encontre$\displaystyle \sum_{n=1}^∞a_n$.

45) Suponha que$ a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),$ onde$ f(n)→0$ como$ n→∞$. Encontre uma condição nos coeficientes$ c_0,…,c_4$ que fazem desta uma série geral de telescópios.

Resposta: $ c_0+c_1+c_2+c_3+c_4=0$

46) Avalie$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}$ (Dica:$\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)}$)

47) Avalie$\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.$

Resposta: $\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1},$
$S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2$

48) Encontre uma fórmula para$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+N)}$ onde$ N$ está um número inteiro positivo.

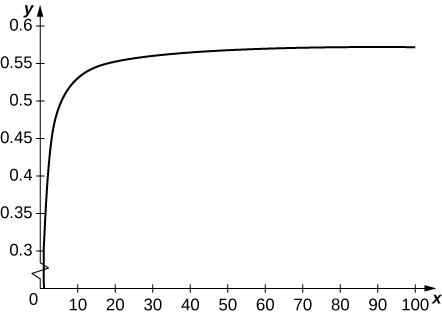
49) [T] Defina uma sequência$\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−\ln k$. Use o gráfico de$ 1/x$ para verificar se$ t_k$ está aumentando. Faça$ t_k$ um gráfico$ k=1…100$ e indique se parece que a sequência converge.

Resposta

$ t_k$converge para$ 0.57721…t_k$ é a soma dos retângulos de altura$ 1/k$ ao longo do intervalo$ [k,k+1]$ que estão acima do gráfico de$ 1/x$.

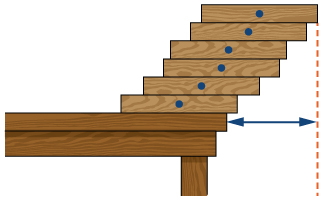
50) [T] Suponha que blocos retangulares uniformes$ N$ iguais estejam empilhados um sobre o outro, permitindo alguma saliência. A lei da alavanca de Arquimedes implica que a pilha de$ N$ blocos é estável desde que o centro de massa dos$ (N−1)$ blocos superiores esteja na borda do bloco inferior. Vamos$ x$ indicar a posição da borda do bloco inferior e pensar em sua posição em relação ao centro do bloco próximo à parte inferior. Isso implica que$ (N−1)x=\left(\frac{1}{2}−x\right)$ ou$ x=1/(2N)$. Use essa expressão para calcular a saliência máxima (a posição da borda do bloco superior sobre a borda do bloco inferior). Veja a figura a seguir.

Cada uma das séries infinitas a seguir converge para o múltiplo dado de$ π$ ou$ 1/π$.

Em cada caso, encontre o valor mínimo de$ N$ tal forma que a soma$ Nth$ parcial da série se aproxime com precisão do lado esquerdo de um determinado número de casas decimais e forneça o valor aproximado desejado. Até a$ 15$ casa decimal,$ π=3.141592653589793....$

51)$\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},$ Erro [T]$ <0.0001$

Resposta: $N=22,$
$S_N=6.1415$

52)$\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},$ erro [T]$ <10^{−4}$

53)$\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},$ erro [T]$ <10^{−12}$

Resposta: $ N=3,$
$S_N=1.559877597243667...$

54) [T]$\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}$, erro$ <10^{−15}$

55) [T] Uma moeda justa é aquela que tem probabilidade$ 1/2$ de ganhar cara ao ser jogada.

a. Qual é a probabilidade de que uma moeda justa apareça$ n$ vezes seguidas?

b. Determine a probabilidade de uma moeda aparecer cara a cara pela primeira vez após um número par de lançamentos de moedas.

Resposta: a. A probabilidade de qualquer sequência ordenada de resultados para lançamentos de$ n$ moedas é$ 1/2^n$.
b. A probabilidade de levantar cabeças pela primeira vez no$ n$ enésimo flip é a probabilidade da sequência$ TT…TH$ que é$ 1/2^n$. A probabilidade de se levantar pela primeira vez em um giro uniforme é$\displaystyle \sum_{n=1}^∞1/2^{2n}$ ou$ 1/3$.

56) [T] Encontre a probabilidade de uma moeda justa ser jogada um múltiplo de três vezes antes de aparecer cara a cara.

57) [T] Descubra a probabilidade de uma moeda justa aparecer cara a cara pela segunda vez após um número par de jogadas.

Resposta: $5/9$

58) [T] Encontre uma série que expresse a probabilidade de uma moeda justa aparecer cara a cara pela segunda vez em um múltiplo de três voltas.

59) [T] O número esperado de vezes que uma moeda justa surgirá cara é definido como a soma$ n=1,2,…$ de$ n$ vezes a probabilidade de a moeda aparecer exatamente$ n$ vezes seguidas, ou$ \dfrac{n}{2^{n+1}}$. Calcule o número esperado de vezes consecutivas em que uma moeda justa surgirá de cabeça para baixo.

Resposta: $\displaystyle E=\sum_{n=1}^∞\frac{n}{2^{n+1}}=1,$como pode ser mostrado usando a soma por partes

60) [T] Uma pessoa deposita$ $10$ no início de cada trimestre em uma conta bancária que ganha juros$ 4%$ anuais compostos trimestralmente (quatro vezes por ano).

a. Mostre que os juros acumulados após os$ n$ trimestres são$ $10(\frac{1.01^{n+1}−1}{0.01}−n).$

b. Encontre os primeiros oito termos da sequência.

c. Quantos juros se acumularam após$ 2$ anos?

61) [T] Suponha que a quantidade de um medicamento no sistema de um paciente diminua em um fator multiplicativo a$ r<1$ cada hora. Suponha que uma nova dose seja administrada a cada$ N$ hora. Encontre uma expressão que forneça a quantidade$ A(n)$ no sistema do paciente após$ n$ horas para cada um$ n$ em termos de dosagem$ d$ e proporção$ r$. (Dica: escreva$ n=mN+k$$ 0≤k<N$, onde e some os valores das diferentes doses administradas.)

Resposta: A parte da primeira dose após$ n$ horas é$ dr^n$, a parte da segunda dose é$ dr^{n−N}$, e, em geral, a parte restante da$ m^{\text{th}}$ dose é$ dr^{n−mN}$, então$\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},\;\text{where}\,n=k+mN.$

62) [T] Um determinado medicamento é eficaz para um paciente médio somente se houver pelo menos$ 1$ mg por kg no sistema do paciente, embora seja seguro somente se houver no máximo$ 2$ mg por kg no sistema de um paciente médio. Suponha que a quantidade no sistema de um paciente diminua por um fator multiplicativo de$ 0.9$ cada hora após a administração de uma dose. Encontre o intervalo máximo$ N$ de horas entre as doses e a faixa de dose correspondente$ d$ (em mg/kg) para$ N$ isso, o que permitirá que o uso do medicamento seja seguro e eficaz a longo prazo.

63) Suponha que$ a_n≥0$ seja uma sequência de números. Explique por que a sequência de somas parciais de$ a_n$ está aumentando.

Resposta: $ S_{N+1}=a_{N+1}+S_N≥S_N$

64) [T] Suponha que$ a_n$ seja uma sequência de números positivos e a sequência$ S_n$ de somas parciais de$ a_n$ esteja limitada acima. Explique por que$\displaystyle \sum_{n=1}^∞a_n$ converge. A conclusão permanece verdadeira se removermos a hipótese$ a_n≥0$?

65) [T] Suponha isso$ a_1=S_1=1$ e aquilo, para determinados números$ S>1$ e$ 0<k<1$,$ a_{n+1}=k(S−S_n)$ defina$ S_{n+1}=a_{n+1}+S_n$ e. $ S_n$Converge? Em caso afirmativo, para quê? (Dica: Primeiro, defenda isso$ S_n<S$ para todos$ n$ e$ S_n$ está aumentando.)

Resposta: Desde$ S>1, a_2>0,$ e desde então$ k<1, S_2=1+a_2<1+(S−1)=S$. Se$ S_n>S$ para alguns$ n$, então há um menor$ n$. Por isso$ n, S>S_{n−1}$, então$ S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S$, uma contradição. Assim$ S_n<S$ e$ a_{n+1}>0$ para todos$ n$, assim$ S_n$ está aumentando e limitado por$ S$. Deixe$\displaystyle S_∗=\lim S_n$. Se$ S_∗<S$, então$ δ=k(S−S_∗)>0$, mas podemos encontrar nada disso, o que implica isso$ S_∗−S_n<δ/2$$ S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2$, contradizendo que o Sol também está aumentando$ S_∗$. Assim$ S_n→S.$

66) [T] Uma versão do crescimento de von Bertalanffy pode ser usada para estimar a idade de um indivíduo em uma espécie homogênea a partir de seu comprimento se o aumento anual no ano for$ n+1$ satisfatório$ a_{n+1}=k(S−S_n)$, com$ S_n$ a duração do ano$ n, S$ como um comprimento limite e$ k$ como constante de crescimento relativo. Se$ S_1=3, S=9,$ e estime$ k=1/2,$ numericamente o menor valor de n de tal forma que$ S_n≥8$. Observe que$ S_{n+1}=S_n+a_{n+1}.$ Encontre o correspondente$ n$ quando$ k=1/4.$

67) [T] Suponha que$\displaystyle \sum_{n=1}^∞a_n$ seja uma série convergente de termos positivos. Explique por que$\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.$

Resposta: Deixe$\displaystyle S_k=\sum_{n=1}^ka_n$$ S_k→L$ e. Então,$ S_k$ eventualmente, se torna arbitrariamente próximo de$ L$, o que significa que$\displaystyle L−S_N=\sum_{n=N+1}^∞a_n$ se torna arbitrariamente pequeno como$ N→∞.$

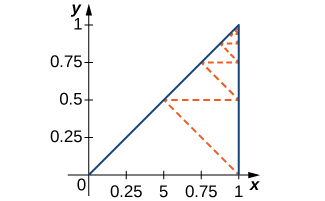
68) [T] Encontre o comprimento do caminho tracejado em zigue-zague na figura a seguir.

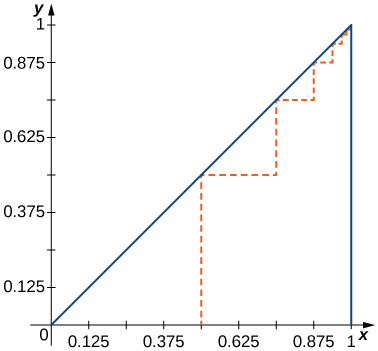
69) [T] Encontre o comprimento total do caminho tracejado na figura a seguir.

Resposta: $\displaystyle L=\left(1+\frac{1}{2}\right)\sum_{n=1}^∞\frac{1}{2^n}=\frac{3}{2}$.

70) [T] O triângulo de Sierpinski é obtido de um triângulo excluindo o quarto do meio conforme indicado na primeira etapa, excluindo os quartos do meio dos três triângulos congruentes restantes na segunda etapa e, em geral, excluindo os quartos do meio dos triângulos restantes em cada um etapa sucessiva. Supondo que o triângulo original seja mostrado na figura, encontre as áreas das partes restantes do triângulo original após$ N$ as etapas e encontre o comprimento total de todos os triângulos limite após$ N$ as etapas.

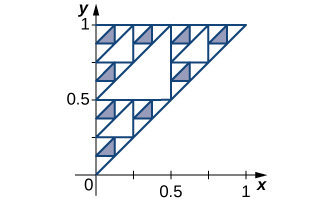
71) [T] A junta de Sierpinski é obtida dividindo o quadrado unitário em nove subquadrados iguais, removendo o quadrado do meio e fazendo o mesmo em cada estágio com os subquadrados restantes. A figura mostra o conjunto restante após quatro iterações. Calcule a área total removida após os$ N$ estágios e calcule o comprimento do perímetro total do conjunto restante após os$ N$ estágios.

Resposta: No estágio um, um quadrado de área$ 1/9$ é removido, no estágio$ 2$ um remove$ 8$ quadrados de área$ 1/9^2$, no estágio três$ 1/9^3$, um$ 8^2$ quadrado de área e assim por diante. A área total removida após os$ N$ estágios é$\displaystyle \sum_{n=0}^{N−1}\frac{8^N}{9^{N+1}}=\frac{1}{8}\cdot\frac{1−(8/9)^N}{1−8/9}→1$ igual$N→∞.$ a O perímetro total é$\displaystyle 4+4\sum_{n=0}^∞\frac{8^N}{3^{N+1}}→∞.$