9.3: A divergência e os testes integrais

Objetivos de

• Use o teste de divergência para determinar se uma série converge ou diverge.
• Use o teste integral para determinar a convergência de uma série.
• Estime o valor de uma série encontrando limites em seu prazo restante.

Na seção anterior, determinamos a convergência ou divergência de várias séries calculando explicitamente o limite da sequência de somas parciais.\( {S_k}.\) Na prática, calcular explicitamente esse limite pode ser difícil ou impossível. Felizmente, existem vários testes que nos permitem determinar a convergência ou divergência para muitos tipos de séries. Nesta seção, discutimos dois desses testes: o teste de divergência e o teste integral. Examinaremos vários outros testes no restante deste capítulo e, em seguida, resumiremos como e quando usá-los.

Teste de divergência

Para\(\displaystyle \sum^∞_{n=1}a_n\) que uma série converja, o\( n^{th}\) termo\( a_n\) deve satisfazer\( a_n→0\) como\( n→∞.\) Portanto, a partir das propriedades de limite algébrico das sequências,

\[\begin{align*} \lim_{k→∞}a_k = \lim_{k→∞}(S_k−S_{k−1}) \\[4pt] =\lim_{k→∞}S_k−\lim_{k→∞}S_{k−1} \\[4pt] =S−S=0. \end{align*}\]

Portanto, se\(\displaystyle \sum_{n=1}^∞a_n\) convergir, o\( n^{th}\) termo\( a_n→0\) como\( n→∞.\) Uma consequência importante desse fato é a seguinte afirmação:

Se\( a_n↛0\) as coisas\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) divergirem.

Esse teste é conhecido como teste de divergência porque fornece uma maneira de provar que uma série diverge.

Definição: O teste de divergência

Se existe\(\displaystyle \lim_{n→∞}a_n=c≠0\) ou\(\displaystyle \lim_{n→∞}a_n\) não, a série\(\displaystyle \sum_{n=1}^∞a_n\) diverge.

É importante observar que o inverso desse teorema não é verdadeiro. Ou seja\(\displaystyle \lim_{n→∞}a_n=0\), se não pudermos fazer nenhuma conclusão sobre a convergência de\(\displaystyle \sum_{n=1}^∞a_n\).

Por exemplo\(\displaystyle \lim_{n→0}\tfrac{1}{n}=0\), mas a série harmônica\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverge. Nesta seção e nas demais seções deste capítulo, mostramos muitos outros exemplos dessas séries. Consequentemente, embora possamos usar o teste de divergência para mostrar que uma série diverge, não podemos usá-lo para provar que uma série converge. Especificamente, se\( a_n→0\), o teste de divergência for inconclusivo.

Exemplo\( \PageIndex{1}\): Using the divergence test

Para cada uma das séries a seguir, aplique o teste de divergência. Se o teste de divergência provar que a série diverge, afirme que sim. Caso contrário, indique que o teste de divergência é inconclusivo.

1. \(\displaystyle \sum^∞_{n=1}\frac{n}{3n−1}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\)
3. \(\displaystyle \sum^∞_{n=1}e^{1/n^2}\)

Solução

1. \(\displaystyle \lim_{n→∞} \frac{n}{3n−1}=\frac{1}{3}≠0\)Pois, pelo teste de divergência, podemos concluir que\(\displaystyle \sum_{n=1}^∞\dfrac{n}{3n−1}\) diverge.
2. Desde então\(\displaystyle \lim_{n→∞} \frac{1}{n^3}=0\), o teste de divergência é inconclusivo.
3. \(\displaystyle \lim_{n→∞} e^{1/n^2}=1≠0\)Pois, pelo teste de divergência, a série\(\displaystyle \sum_{n=1}^∞e^{1/n^2}\) diverge.

Exercício\( \PageIndex{1}\)

O que o teste de divergência nos diz sobre a série\(\displaystyle \sum_{n=1}^∞\cos(1/n^2)\)?

Dica

Veja\(\displaystyle \lim_{n→∞}\cos(1/n^2)\).

Responda

A série diverge.

Teste integral

Na seção anterior, provamos que a série harmônica diverge observando a sequência de somas parciais\( {S_k}\) e mostrando isso\( S_{2^k}>1+k/2\) para todos os números inteiros positivos\( k\). Nesta seção, usamos uma técnica diferente para provar a divergência da série harmônica. Essa técnica é importante porque é usada para provar a divergência ou convergência de muitas outras séries. Esse teste, chamado de teste integral, compara uma soma infinita com uma integral imprópria. É importante observar que esse teste só pode ser aplicado quando estamos considerando uma série cujos termos são todos positivos.

Figura\(\PageIndex{1}\) : A soma das áreas dos retângulos é maior do que a área entre a curva\( f(x)=1/x\) e o\( x\) eixo -de\( x≥1\). Como a área delimitada pela curva é infinita (calculada por uma integral imprópria), a soma das áreas dos retângulos também é infinita.

Para ilustrar como o teste integral funciona, use a série harmônica como exemplo. Na Figura\(\PageIndex{1}\), descrevemos a série harmônica esboçando uma sequência de retângulos com áreas\( 1,1/2,1/3,1/4,…\) junto com a função\( f(x)=1/x.\) Do gráfico, vemos que

\[\sum_{n=1}^k\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+⋯+\dfrac{1}{k}>∫^{k+1}_1\dfrac{1}{x}\,dx. \nonumber \]

Portanto, para cada um\( k\), a soma\( k^{\text{th}}\) parcial\( S_k\) satisfaz

\[\begin{align*} S_k =\sum_{n=1}^k\dfrac{1}{n} >∫^{k+1}_1\dfrac{1}{x}\,dx = \ln x \big| ^{k+1}_1 \\[4pt] = \ln (k+1)−\ln (1) \\[4pt] =\ln (k+1).\end{align*}\]

Pois\(\displaystyle \lim_{k→∞}\ln(k+1)=∞,\) vemos que a sequência de somas parciais\( {S_k}\) é ilimitada. Portanto,\( {S_k}\) diverge e, consequentemente, a série\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n}\) também diverge.

Figura\(\PageIndex{2}\): A soma das áreas dos retângulos é menor que a soma da área do primeiro retângulo e da área entre a curva\( f(x)=1/x^2\) e o\( x\) eixo -de\( x≥1\). Como a área delimitada pela curva é finita, a soma das áreas dos retângulos também é finita.

Agora, considere a série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Mostramos como uma integral pode ser usada para provar que essa série converge. Na Figura\(\PageIndex{2}\), esboçamos uma sequência de retângulos com áreas\( 1,1/2^2,1/3^2,…\) junto com a função\( f(x)=\frac{1}{x^2}\). A partir do gráfico, vemos que

\[\sum_{n=1}^k\dfrac{1}{n^2}=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+⋯+\dfrac{1}{k^2}<1+∫^k_1\dfrac{1}{x^2}\,dx. \nonumber \]

Portanto, para cada um\( k\), a soma\( k^{\text{th}}\) parcial\( S_k\) satisfaz

\[\begin{align*} S_k=\sum_{n=1}^k\dfrac{1}{n^2}<1+∫^k_1\dfrac{1}{x^2}\,dx =1−\left. \dfrac{1}{x} \right|^k_1 \\[4pt] =1−\dfrac{1}{k}+1 \\[4pt] =2−\dfrac{1}{k}<2. \end{align*}\]

Concluímos que a sequência de somas parciais\( {S_k}\) é limitada. Também vemos que\( {S_k}\) é uma sequência crescente:

\[S_k=S_{k−1}+\dfrac{1}{k^2} \nonumber \]

para\( k≥2\).

Como\( {S_k}\) é crescente e limitado, pelo Teorema da Convergência Monótona, ele converge. Portanto, a série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converge.

Figura\(\PageIndex{3}\): (a) Se pudermos inscrever retângulos dentro de uma região delimitada por uma curva\( y=f(x)\) e pelo\( x\) eixo -, e a área delimitada por essas curvas\( x≥1\) for finita, a soma das áreas dos retângulos também é finita. (b) Se um conjunto de retângulos circunscreve a região delimitada por\( y=f(x)\) e o\( x\) eixo para\( x≥1\) a região tem área infinita, então a soma das áreas dos retângulos também é infinita.

Podemos estender essa ideia para provar convergência ou divergência para muitas séries diferentes. Suponha que\(\displaystyle \sum^∞_{n=1}a_n\) seja uma série com termos positivos de\( a_n\) forma que exista uma função\( f\) contínua, positiva e decrescente\( f(n)=a_n\) para todos os números inteiros positivos. Então, como na Figura\(\PageIndex{3a}\), para qualquer número inteiro\( k\), a soma\( k^{\text{th}}\) parcial\( S_k\) satisfaz

\[S_k=a_1+a_2+a_3+⋯+a_k<a_1+∫^k_1f(x)\,dx<1+∫^∞_1f(x)\,dx. \nonumber \]

Portanto, se\(\displaystyle ∫^∞_1f(x)\,dx\) convergir, a sequência de somas parciais\( {S_k}\) é limitada. Como\( {S_k}\) é uma sequência crescente, se também for uma sequência limitada, então, pelo Teorema da Convergência Monótona, ela converge. Concluímos que, se\(\displaystyle ∫^∞_1f(x)\,dx\) converge, a série\(\displaystyle \sum^∞_{n=1}a_n\) também converge. Por outro lado, da Figura\(\PageIndex{3b}\), para qualquer número inteiro\( k\), a soma\( k^{\text{th}}\) parcial\( S_k\) satisfaz

\[S_k=a_1+a_2+a_3+⋯+a_k>∫^{k+1}_1f(x)\,dx. \nonumber \]

E se

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞, \nonumber \]

então\( {S_k}\) é uma sequência ilimitada e, portanto, diverge. Como resultado, a série\(\displaystyle \sum_{n=1}^∞a_n\) também diverge. Uma vez que\( f\) é uma função positiva, se\(\displaystyle ∫^∞_1f(x)\,dx\) diverge, então

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞. \nonumber \]

Concluímos que se\(\displaystyle ∫^∞_1f(x)\,dx\) diverge, então\(\displaystyle \sum_{n=1}^∞a_n\) diverge.

Definição: O Teste Integral

Suponha que\(\displaystyle \sum_{n=1}^∞a_n\) seja uma série com termos positivos\( a_n\). Suponha que exista uma função\( f\) e um número inteiro positivo de\( N\) forma que as três condições a seguir sejam satisfeitas:

1. \( f\)é contínuo,
2. \( f\)está diminuindo, e
3. \( f(n)=a_n\)para todos os números inteiros\( n≥N.\)

Então

\[\sum_{n=1}^∞a_n \nonumber \]

e

\[∫^∞_Nf(x)\,dx \nonumber \]

ambos convergem ou ambos divergem (Figura\(\PageIndex{3}\)).

Embora a convergência de\(\displaystyle ∫^∞_Nf(x)\,dx\) implique convergência da série relacionada\(\displaystyle \sum_{n=1}^∞a_n\), isso não implica que o valor da integral e da série sejam os mesmos. Eles podem ser diferentes, e muitas vezes são. Por exemplo,

\[\sum_{n=1}^∞\left(\dfrac{1}{e}\right)^n=\dfrac{1}{e}+\left(\dfrac{1}{e}\right)^2+\left(\dfrac{1}{e}\right)^3+⋯ \nonumber \]

é uma série geométrica com termo\( a=1/e\) e proporção iniciais\( r=1/e,\) que converge para

\[\dfrac{1/e}{1−(1/e)}=\dfrac{1/e}{(e−1)/e}=\dfrac{1}{e−1}. \nonumber \]

No entanto, a integral relacionada\(\displaystyle ∫^∞_1(1/e)^x\,dx\) satisfaz

\[∫^∞_1\left(\frac{1}{e}\right)^x\,dx=∫^∞_1e^{−x}\,dx=\lim_{b→∞}∫^b_1e^{−x}\,dx=\lim_{b→∞}−e^{−x}\big|^b_1=\lim_{b→∞}[−e^{−b}+e^{−1}]=\dfrac{1}{e}. \nonumber \]

Exemplo\( \PageIndex{2}\): Using the Integral Test

Para cada uma das séries a seguir, use o teste integral para determinar se a série converge ou diverge.

1. \(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{\sqrt{2n−1}}\)

Solução

a. Compare

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\)e\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx.\)

Nós temos

\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\bigg|^b_1\right]=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2}\right]=\dfrac{1}{2}.\)

Assim, a integral\(\displaystyle ∫^∞_1\frac{1}{x^3}\,dx\) converge e, portanto, a série também

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\).

b. Compare

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{\sqrt{2n−1}}\)\(\displaystyle ∫^∞_1\dfrac{1}{\sqrt{2x−1}}\,dx\)e.

Desde

\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}∫^b_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}\sqrt{2x−1}\bigg|^b_1=\lim_{b→∞}\left[\sqrt{2b−1}−1\right]=∞,\)

a integral\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx\) diverge e, portanto,

\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{2n−1}}\)

diverge.

Exercício\( \PageIndex{2}\)

Use o teste integral para determinar se a série\(\displaystyle \sum^∞_{n=1}\dfrac{n}{3n^2+1}\) converge ou diverge.

Dica

Compare com o integral\(\displaystyle ∫^∞_1\dfrac{x}{3x^2+1}\,dx.\)

Responda

A série diverge.

A\(p\) Série E

A série harmônica\(\displaystyle \sum^∞_{n=1}1/n\) e a série\(\displaystyle \sum^∞_{n=1}1/n^2\) são exemplos de um tipo de série chamado série p.

Definição:\(p\)-series

Para qualquer número real\( p\), a série

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

é chamado de série P.

Sabemos que a\(p\) série -converge if\( p=2\) e diverge if\( p=1\). E quanto aos outros valores de\( p\)? Em geral, é difícil, se não impossível, calcular o valor exato da maioria das\( p\) séries. No entanto, podemos usar os testes apresentados até agora para provar se uma\( p\) série -converge ou diverge.

Se\( p<0,\) então\( 1/n^p→∞,\) e se\( p=0\), então\( 1/n^p→1.\) Portanto, pelo teste de divergência,

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

diverge se\(p≤0\).

Se\( p>0,\) então\( f(x)=1/x^p\) é uma função positiva, contínua e decrescente. Portanto, para\( p>0,\) nós usamos o teste integral, comparando

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]e\[∫^∞_1\dfrac{1}{x^p}\,dx. \nonumber \]

Já consideramos o caso quando\( p=1.\) Aqui consideramos o caso quando\( p>0,p≠1.\) Para este caso,

\[∫^∞_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}\dfrac{1}{1−p}x^{1−p}∣^b_1=\lim_{b→∞}\dfrac{1}{1−p}[b^{1−p}−1]. \nonumber \]

Porque

\( b^{1−p}→0\)se\( p>1\) e\( b^{1−p}→∞\) se\( p<1,\)

concluímos que

\[∫^∞_1\dfrac{1}{x^p}\,dx=\begin{cases}\dfrac{1}{p−1}, \text{if}\;p>1\\ ∞, \text{if}\;p<1.\end{cases} \nonumber \]

Portanto,\(\displaystyle \sum^∞_{n=1}1/n^p\) converge se\( p>1\) e diverge se\( 0<p<1.\)

Em resumo,

\[\sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges} \text{if}\; p>1\\ \text{diverges} \text{if}\;p≤1\end{cases} \nonumber \].

Exemplo\( \PageIndex{3}\): Testing for Convergence of p-series

Para cada uma das séries a seguir, determine se ela converge ou diverge.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^4}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{2/3}}\)

Solução

1. Esta é uma\(p\) série -com\( p=4>1\), então a série converge.
2. Já que\( p=2/3<1,\) a série diverge.

Exercício\( \PageIndex{3}\)

A série\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{5/4}}\) converge ou diverge?

Dica

\( p=5/4\)

Responda

A série converge.

Estimando o valor de uma série

Suponha que saibamos que uma série\(\displaystyle \sum_{n=1}^∞a_n\) converge e queremos estimar a soma dessa série. Certamente podemos aproximar essa soma usando qualquer soma finita\(\displaystyle \sum_{n=1}^Na_n\) onde\( N\) esteja qualquer número inteiro positivo. A questão que abordamos aqui é, para uma série convergente\(\displaystyle \sum^∞_{n=1}a_n\), quão boa é a aproximação\(\displaystyle \sum^N_{n=1}a_n\)?

Mais especificamente, se deixarmos

\[R_N=\sum_{n=1}^∞a_n−\sum_{n=1}^Na_n \nonumber \]

seja o restante quando a soma de uma série infinita é aproximada pela soma\(N^{\text{th}}\) parcial, qual é o tamanho\( R_N\)? Para alguns tipos de séries, podemos usar as ideias do teste integral para estimar\( R_N\).

Nota\(\PageIndex{1}\): Remainder Estimate from the Integral Test

Suponha que\(\displaystyle \sum^∞_{n=1}a_n\) seja uma série convergente com termos positivos. Suponha que exista uma função\( f\) que satisfaça as três condições a seguir:

1. \( f\)é contínuo,
2. \( f\)está diminuindo, e
3. \( f(n)=a_n\)para todos os números inteiros\( n≥1.\)

\( S_N\)Seja a soma\(N^{\text{th}}\) parcial de\(\displaystyle \sum^∞_{n=1}a_n\). Para todos os números inteiros positivos\( N\),

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Em outras palavras, o restante\(\displaystyle R_N=\sum^∞_{n=1}a_n−S_N=\sum^∞_{n=N+1}a_n\) satisfaz a seguinte estimativa:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Isso é conhecido como estimativa do restante.

Ilustramos o Note\(\PageIndex{1}\) in Figure\(\PageIndex{4}\). Em particular, representando o restante\( R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯\) como a soma das áreas dos retângulos, vemos que a área desses retângulos é limitada acima\(\displaystyle ∫^∞_Nf(x)\,dx\) e delimitada abaixo por\(\displaystyle ∫^∞_{N+1}f(x)\,dx.\) Em outras palavras,

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx \nonumber \]

e

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx. \nonumber \]

Concluímos que

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Desde

\[\sum_{n=1}^∞a_n=S_N+R_N, \nonumber \]

onde\( S_N\) está a soma\(N^{\text{th}}\) parcial, concluímos que

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Figura\(\PageIndex{4}\): Dada uma função contínua, positiva e decrescente\( f\) e uma sequência de termos positivos de\( a_n\) forma que,\( a_n=f(n)\) para todos os números inteiros positivos\( n\), (a) as áreas\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx\) ou (b) as áreas\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx\). Portanto, a integral é uma superestimação ou uma subestimação do erro.

Exemplo\( \PageIndex{4}\): Estimating the Value of a Series

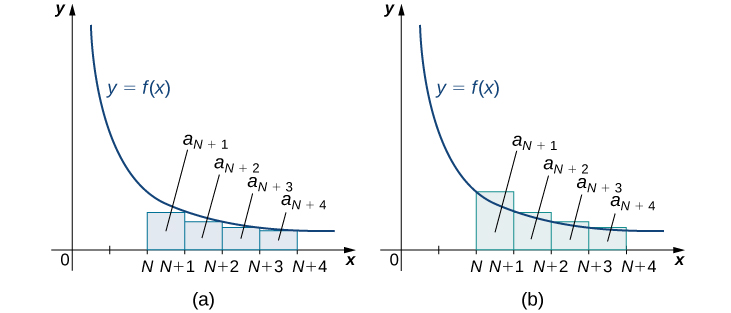
Considere a série\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\).

1. \(\displaystyle S_{10}=\sum^{10}_{n=1}\frac{1}{n^3}\)Calcule e estime o erro.
2. Determine o menor valor\( N\) necessário de tal forma que\( S_N\) será estimado\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\) para dentro\( 0.001\).

Solução

a. Usando um utilitário de cálculo, temos

\[ S_{10}=1+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3}+⋯+\dfrac{1}{10^3}≈1.19753. \nonumber \]

Pela estimativa restante, sabemos

\[ R_N<∫^∞_N\dfrac{1}{x^3}\,dx. \nonumber \]

Nós temos

\[ ∫^∞_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\right]^b_N=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2N^2}\right]=\dfrac{1}{2N^2}. \nonumber \]

Portanto, o erro é\( R_{10}<1/2(10)^2=0.005.\)

b. Encontre\( N\) tal coisa\( R_N<0.001\). Na parte a. mostramos isso\( R_N<1/2N^2\). Portanto, o restante é\( R_N<0.001\) tão longo quanto\( 1/2N^2<0.001\). Ou seja, precisamos\( 2N^2>1000\). Resolvendo essa desigualdade para\( N\), vemos que precisamos\( N>22.36\). Para garantir que o restante esteja dentro do valor desejado, precisamos arredondar para o número inteiro mais próximo. Portanto, o valor mínimo necessário é\( N=23\).

Exercício\( \PageIndex{4}\)

Para\(\displaystyle \sum^∞_{n=1}\frac{1}{n^4}\),\( S_5\) calcule e estime o erro\( R_5\).

Dica

Use a estimativa restante\(\displaystyle R_N<∫^∞_N\frac{1}{x^4}\,dx.\)

Responda

\( S_5≈1.09035, R_5<0.00267\)

Conceitos-chave

• Nesse caso\(\displaystyle \lim_{n→∞}a_n≠0,\), a série\(\displaystyle \sum^∞_{n=1}a_n\) diverge.
• Se\(\displaystyle \lim_{n→∞}a_n=0,\) a série\(\displaystyle \sum^∞_{n=1}a_n\) puder convergir ou divergir.
• Se\(\displaystyle \sum^∞_{n=1}a_n\) for uma série com termos positivos\( a_n\) e\( f\) for uma função contínua e decrescente, de forma que,\( f(n)=a_n\) para todos os números inteiros positivos\( n\), então

\[\sum_{n=1}^∞a_n \nonumber \]e\[∫^∞_1f(x)\,dx \nonumber \]

ambos convergem ou ambos divergem. Além disso, se\(\displaystyle \sum^∞_{n=1}a_n\) convergir, a aproximação da soma\(N^{\text{th}}\) parcial\( S_N\) é precisa até um erro\( R_N\) em que\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\).

• A\(p\) série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^p}\) -converge se\( p>1\) e diverge se\( p≤1.\)

Equações-chave

• Teste de divergência

Se\( a_n↛0\) as coisas\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) divergirem.

• série p

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges}, \text{if}\;p>1\\\text{diverges}, \text{if}\; p≤1\end{cases}\)

• Estimativa do restante do teste integral

\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\)

Glossário

teste de divergência

se\(\displaystyle \lim_{n→∞}a_n≠0,\) então a série\(\displaystyle \sum^∞_{n=1}a_n\) diverge

teste integral

para uma série\(\displaystyle \sum^∞_{n=1}a_n\) com termos positivos\( a_n\), se existir uma função contínua e decrescente\( f\) tal que\( f(n)=a_n\) para todos os números inteiros positivos\( n\), então

\[\sum_{n=1}^∞a_n \nonumber \]e\[∫^∞_1f(x)\,dx \nonumber \]

ambos convergem ou ambos divergem

série p

uma série do formulário\(\displaystyle \sum^∞_{n=1}1/n^p\)

estimativa do restante

para uma série\(\displaystyle \sum^∞_{n=}1a_n\) com termos positivos\( a_n\) e uma função contínua decrescente de\( f\) forma que,\( f(n)=a_n\) para todos os números inteiros positivos\( n\), o restante\(\displaystyle R_N=\sum^∞_{n=1}a_n−\sum^N_{n=1}a_n\) satisfaça a seguinte estimativa:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx \nonumber \]