9.1E: Exercícios para a Seção 9.1

Last updated
Save as PDF

Page ID: 188435

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, encontre os primeiros seis termos de cada sequência, começando com$ n=1$.

1)$a_n=1+(−1)^n$ para$ n≥1$

Responda: $ a_n=0$se$ n$ é estranho e$ a_n=2$ se$ n$ é par

2)$ a_n=n^2−1$ para$ n≥1$

3)$ a_1=1$ e$ a_n=a_{n−1}+n$ para$ n≥2$

Responda: $ {a_n}={1,3,6,10,15,21,…}$

4)$ a_1=1, a_2=1$ e$ a_n+2=a_n+a_{n+1}$ para$ n≥1$

5) Encontre uma fórmula explícita para$ a_n$ onde$ a_1=1$ e$ a_n=a_{n−1}+n$ para$ n≥2$.

Responda: $ a_n=\dfrac{n(n+1)}{2}$

6) Encontre uma fórmula$ a_n$ para o$n^{\text{th}}$ termo da progressão aritmética cujo primeiro termo seja$ a_1=1$ tal que$ a_{n−1}−a_n=17$ para$ n≥1$.

7) Encontre uma fórmula$ a_n$ para o$n^{\text{th}}$ termo da progressão aritmética cujo primeiro termo seja$ a_1=−3$ tal que$ a_{n−1}−a_n=4$ para$ n≥1$.

Responda: $ a_n=4n−7$

8) Encontre uma fórmula$ a_n$ para o$n^{\text{th}}$ termo da sequência geométrica cujo primeiro termo seja$ a_1=1$ tal que$ \dfrac{a_{n+1}}{a_n}=10$ para$ n≥1$.

9) Encontre uma fórmula$ a_n$ para o$n^{\text{th}}$ termo da sequência geométrica cujo primeiro termo seja$ a_1=3$ tal que$ \dfrac{a_{n+1}}{a_n}=1/10$ para$ n≥1$.

Responda: $ a_n=3.10^{1−n}=30.10^{−n}$

10) Encontre uma fórmula explícita para o$n^{\text{th}}$ termo da sequência cujos primeiros termos são$ {0,3,8,15,24,35,48,63,80,99,…}.$ (Dica: primeiro adicione um a cada termo.)

11) Encontre uma fórmula explícita para o$n^{\text{th}}$ termo da sequência satisfatória$ a_1=0$ e$ a_n=2a_{n−1}+1$ para$ n≥2$.

Responda: $ a_n=2^n−1$

Nos exercícios 12 e 13, encontre uma fórmula para o termo geral$ a_n$ de cada uma das seguintes sequências.

12)$ {1,0,−1,0,1,0,−1,0,…}$ (Dica: Descubra onde$\sin x$ leva esses valores)

13)$ {1,−1/3,1/5,−1/7,…}$

Responda: $ a_n=\dfrac{(−1)^{n−1}}{2n−1}$

Nos exercícios 14-18, encontre uma função$ f(n)$ que identifique o$n^{\text{th}}$ termo$ a_n$ das seguintes sequências recursivamente definidas, como$ a_n=f(n)$.

14)$ a_1=1$ e$ a_{n+1}=−a_n$ para$ n≥1$

15)$ a_1=2$ e$ a_{n+1}=2a_n$ para$ n≥1$

Responda: $ f(n)=2^n$

16)$ a_1=1$ e$ a_{n+1}=(n+1)a_n$ para$ n≥1$

17)$ a_1=2$ e$ a_{n+1}=(n+1)a_n/2$ para$ n≥1$

Responda: $f(n)=\dfrac{n!}{2^{n-2}}$

18)$ a_1=1$ e$ a_{n+1}=a_n/2^n$ para$ n≥1$

Nos exercícios 19 a 22, plote os primeiros$ N$ termos da sequência dada. Indique se a evidência gráfica sugere que a sequência converge ou diverge.

19) [T]$ a_1=1, a_2=2$ e para$ n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2})$;$ N=30$

Responda

Os termos oscilam acima$ 5/3$ e abaixo e parecem convergir para$ 5/3$.

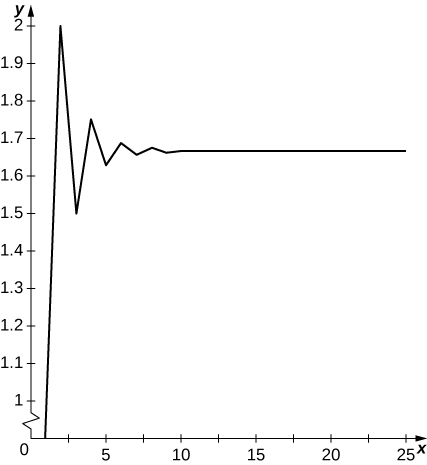
20) [T]$ a_1=1, a_2=2, a_3=3$ e para$ n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30$

21) [T]$ a_1=1, a_2=2$ e para$ n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30$

Responda

Os termos oscilam acima$ y≈1.57..$ e abaixo e parecem convergir até um limite.

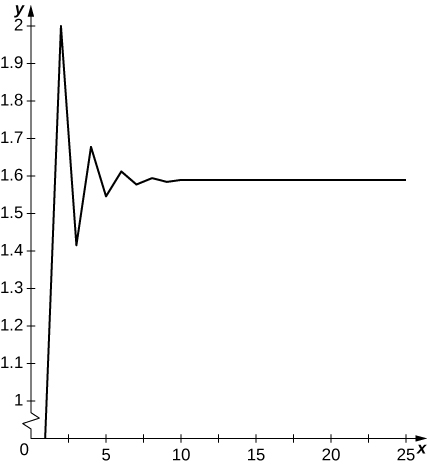
22) [T]$ a_1=1, a_2=2, a_3=3$ e para$ n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30$

Nos exercícios 23 a 16, suponha isso$\displaystyle \lim_{n→∞}a_n=1, $$\displaystyle \lim_{n→∞}b_n=−1$ e$ 0<−b_n<a_n$ para todos$ n$.

Usando essas informações, avalie cada um dos limites a seguir, declare que o limite não existe ou afirme que não há informações suficientes para determinar se o limite existe.

23)$\displaystyle \lim_{n→∞}3a_n−4b_n$

Responda: $\displaystyle \lim_{n→∞}3a_n−4b_n \quad = \quad 7$

24)$\displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n$

25)$\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}$

Responda: $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n} \quad = \quad 0$

26)$\displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}$

Nos exercícios 27 a 30, determine o limite de cada uma das seguintes sequências, usando a regra de L'Hôpital quando apropriado.

27)$ \dfrac{n^2}{2^n}$

Responda: $\displaystyle \lim_{n→∞} \dfrac{n^2}{2^n} \quad = \quad 0$

28)$ \dfrac{(n−1)^2}{(n+1)^2}$

29)$ \dfrac{\sqrt{n}}{\sqrt{n+1}}$

Responda: $\displaystyle \lim_{n→∞} \dfrac{\sqrt{n}}{\sqrt{n+1}} \quad = \quad 1 $

30)$ n^{1/n}$ (Dica:$ n^{1/n}=e^{\frac{1}{n}\ln n})$

Nos exercícios 31 a 37, indique se cada sequência é limitada e se é eventualmente monótona, crescente ou decrescente.

31)$ n/2^n, n≥2$

Responda: limitado, diminuindo para$ n≥1$

32)$ \ln\left(1+\dfrac{1}{n}\right)$

33)$ \sin n$

Responda: limitado, não monótono

34)$ \cos(n^2)$

(35)$ n^{1/n}, \quad n≥3$

Responda: limitado, decrescente

36)$ n^{−1/n}, \quad n≥3$

37)$ \tan n$

Responda: não monótono, não limitado

Nos exercícios 38 a 39, determine se a sequência dada tem um limite. Se isso acontecer, encontre o limite.

38)$ a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}}$ etc.

39)$ a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….$

Responda: $ a_n$está diminuindo e limitado abaixo por$2$. O limite a deve satisfazer$ a=\sqrt{2a}$ isso$ a=2$, independente do valor inicial.

Use o Teorema de Squeeze para encontrar o limite de cada sequência nos exercícios 40 a 43.

40)$ n\sin(1/n)$

41)$ \dfrac{\cos(1/n)−1}{1/n}$

Responda: $0$

(42)$ a_n=\dfrac{n!}{n^n}$

43)$ a_n=\sin n \sin(1/n)$

Responda: $ 0$desde então$|\sin x|≤|x|$ e$ |\sin x|≤1$ assim por diante$ −\dfrac{1}{n}≤a_n≤\dfrac{1}{n})$.

Para as sequências nos exercícios 44 e 45, plote os primeiros$ 25$ termos da sequência e indique se a evidência gráfica sugere que a sequência converge ou diverge.

44) [T]$ a_n=\sin n$

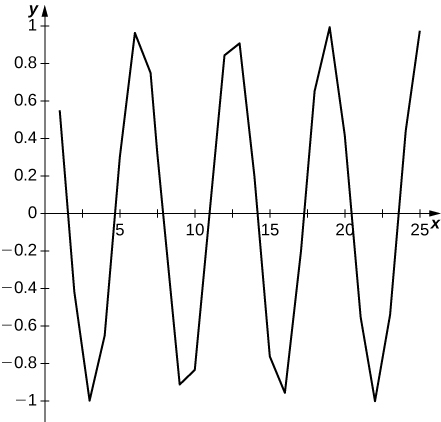
45) [T]$ a_n=\cos n$

Responda

O gráfico oscila e não sugere limite.

Nos exercícios 46 a 52, determine o limite da sequência ou mostre que a sequência diverge. Se ele convergir, encontre seu limite.

(46)$ a_n=\tan^{−1}(n^2)$

47)$ a_n=(2n)^{1/n}−n^{1/n}$

Responda: $ n^{1/n}→1$e$ 2^{1/n}→1,$ assim$ a_n→0$

48)$ a_n=\dfrac{\ln(n^2)}{\ln(2n)}$

49)$ a_n=\left(1−\frac{2}{n}\right)^n$

Responda: Desde então$ (1+1/n)^n→e$, um tem$ (1−2/n)^n≈(1+k)^{−2k}→e^{−2}$ como$ k→∞.$

50)$ a_n=\ln\left(\dfrac{n+2}{n^2−3}\right)$

51)$ a_n=\dfrac{2^n+3^n}{4^n}$

Responda: $ 2^n+3^n≤2⋅3^n$e$ 3^n/4^n→0$ como$ n→∞$, assim$ a_n→0$ como$ n→∞.$

52)$ a_n=\dfrac{(1000)^n}{n!}$

53)$ a_n=\dfrac{(n!)^2}{(2n)!}$

Responda: $ \dfrac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\dfrac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n$. Em particular$ a_{n+1}/a_n≤1/2$, assim$ a_n→0$ como$ n→∞$.

O método de Newton busca aproximar uma solução$ f(x)=0$ que começa com uma aproximação inicial$ x_0$ e define sucessivamente uma sequência$ x_{n+1}=x_n−\dfrac{f(x_n)}{f′(x_n)}$. Para a escolha dada de$ f$ e$ x_0$, escreva a fórmula para$ x_{n+1}$. Se a sequência parecer convergir, forneça uma fórmula exata para a solução e$ x$, em seguida, identifique o limite com$ x$ precisão de quatro casas decimais e o menor$ n$ que esteja de$ x_n$ acordo com$ x$ até quatro casas decimais.

54) [T]$ f(x)=x^2−2,\quad x_0=1$

55) [T]$ f(x)=(x−1)^2−2,\quad x_0=2$

Responda: \ (x_ {n+1} =x_n− ((x_n−1) ^2−2) /2 (x_n−1);\;
x=1+\ sqrt {2},\; x≈ 2,4142,\; n=5\)

56) [T]$ f(x)=e^x−2, \quad x_0=1$

57) [T]$ f(x)=\ln x−1,\quad x_0=2$

Responda: \ (x_ {n+1} =x_n−x_n (\ ln (x_n) −1);\;
x=e,\; x≈ 2,7183,\; n=5\)

58) [T] Suponha que você comece com um litro de vinagre e remova repetidamente$0.1$ L, substitua por água, misture e repita.

a. Encontre uma fórmula para a concentração após$ n$ as etapas.

b. Depois de quantas etapas a mistura contém menos do que$ 10\%$ vinagre?

59) [T] Um lago inicialmente contém$ 2000$ peixes. Suponha que, na ausência de predadores ou outras causas de remoção, a população de peixes aumente a$ 6\%$ cada mês. No entanto, considerando todas as causas, os$ 150$ peixes são perdidos a cada mês.

a. Explique por que a população de peixes após$ n$ meses é modelada$ P_n=1.06P_{n−1}−150$ com$ P_0=2000$.

b. Quantos peixes estarão na lagoa após um ano?

Responda: a. Sem perdas, a população obedeceria$ P_n=1.06P_{n−1}$. A subtração de$ 150$ contas para perdas de peixes.
b. Depois de$ 12$ meses, temos$ P_{12}≈1494.$

60) [T] Uma conta bancária ganha$ 5\%$ juros compostos mensalmente. Suponha que$ $1000$ seja inicialmente depositado na conta, mas que$ $10$ seja retirado a cada mês.

a. Mostre que o valor na conta após$ n$ meses é$ A_n=(1+.05/12)A_{n−1}−10; \; A_0=1000.$

b. Quanto dinheiro estará na conta após um$ 1$ ano?

c. O valor está aumentando ou diminuindo?

d. Suponha que, em vez de$ $10$, uma quantia fixa em$ d$ dólares seja retirada a cada mês. Encontre um valor$ d$ tal que o valor na conta após cada mês permaneça$ $1000$.

e. O que acontece se$ d$ for maior do que esse valor?

61) [T] Um estudante contrai um empréstimo universitário de uma$ $10,000$ taxa percentual anual de$ 6\%,$ compostos mensais.

a. Se o aluno fizer pagamentos$ $100$ por mês, quanto ele deve depois de$ 12$ meses?

b. Depois de quantos meses o empréstimo será pago?

Responda: a. O estudante deve$ $9383$ depois de$ 12$ meses.
b. O empréstimo será pago integralmente após$ 139$ meses ou onze anos e meio.

62) [T] Considere uma série que combina crescimento geométrico e diminuição aritmética. Deixe$ a_1=1$. Corrigir$ a>1$$ 0<b<a$ e. Defina$ a_{n+1}=a.a_n−b.$ Encontre uma fórmula para$ a_{n+1}$ em termos de$ a_n, a$, e$ b$ e uma relação entre$ a$ e$ b$ tal que$ a_n$ converja.

63) [T] A representação binária$ x=0.b_1b_2b_3...$ de um número$ x$ entre$ 0$ e$ 1$ pode ser definida da seguinte forma. Deixe$ b_1=0$ se$ x<1/2$ e$ b_1=1$ se for$ 1/2≤x<1.$$ x_1=2x−b_1$. Deixe$ b_2=0$ se$ x_1<1/2$ e$ b_2=1$ se$ 1/2≤x<1$. Deixe$ x_2=2x_1−b_2$ e, em geral,$ x_n=2x_{n−1}−b_n$ e$ b_{n−}1=0$ se$ x_n<1/2$ e$ b_{n−1}=1$ se$ 1/2≤x_n<1$. Encontre a expansão binária de$ 1/3$.

Responda: $ b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3,$então o padrão se repete, e$ 1/3=0.010101….$

64) [T] Para encontrar uma aproximação para$ π$, definir e$ a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}$, em geral,$ a_{n+1}=\sqrt{2+a_n}$. Finalmente, defina$ p_n=3.2^n\sqrt{2−a_n}$. Encontre os primeiros dez termos de$ p_n$ e compare os valores com$ π$.

Para os dois exercícios a seguir, suponha que você tenha acesso a um programa de computador ou fonte da Internet que possa gerar uma lista de zeros e uns de qualquer tamanho desejado. Os geradores de números pseudo-aleatórios (PRNGs) desempenham um papel importante na simulação de ruídos aleatórios em sistemas físicos, criando sequências de zeros e uns que aparecem como o resultado de jogar uma moeda repetidamente. Um dos tipos mais simples de PRNGs define recursivamente uma sequência aleatória de$ N$ números inteiros$ a_1,a_2,…,a_N$ fixando dois inteiros especiais$ (K$$ M$ e deixando$ a_{n+1}$ ser o restante após a divisão$ K.a_n$ em$ M$, então cria uma sequência de bits de zeros e unidades cujo $n^{\text{th}}$termo$ b_n$ é igual a um se$ a_n$ for ímpar e igual a zero se$ a_n$ for par. Se os bits$ b_n$ forem pseudo-aleatórios, o comportamento de sua média$ (b_1+b_2+⋯+b_N)/N$ deve ser semelhante ao comportamento das médias dos bits realmente gerados aleatoriamente.

65) [T] Começando com$ K=16,807$ e$ M=2,147,483,647$, usando dez valores iniciais diferentes de$ a_1$, calcule sequências de bits$ b_n$ até$ n=1000,$ e compare suas médias com dez sequências geradas por um gerador de bits aleatório.

Responda: Para os valores$ a_1=1, a_2=2,…, a_1=10,$ iniciais, as médias de bits correspondentes calculadas pelo método indicado são$ 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040,$$ 0.4840$ e. Aqui está um exemplo de dez médias correspondentes de sequências de$ 1000$ bits geradas por um gerador de números aleatórios: Não$ 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980.$ há padrão real em nenhum tipo de média. As médias geradas por números aleatórios variam entre$ 0.4860$ e$ 0.5490$, uma faixa de$ 0.0630$, enquanto as médias de bits PRNG calculadas variam entre$ 0.4680$ e$ 0.5220$, uma faixa de$ 0.0540.$

66) [T] Encontre os primeiros$ 1000$ dígitos$ π$ usando um programa de computador ou recurso da Internet. Crie uma sequência de bits$ b_n$ deixando$ b_n=1$ se o$n^{\text{th}}$ dígito de$ π$ é ímpar e$ b_n=0$ se o$n^{\text{th}}$ dígito de$ π$ é par. Calcule o valor médio$ b_n$ e o valor médio de$ d_n=|b_{n+1}−b_n|, n=1,...,999.$ A sequência$ b_n$ parece aleatória? As diferenças entre os elementos sucessivos do$ b_n$ parecem aleatórias?