9.1: Sequências

objetivos de aprendizagem

• Encontre a fórmula para o termo geral de uma sequência.
• Calcule o limite de uma sequência, se ela existir.
• Determine a convergência ou divergência de uma determinada sequência.

Nesta seção, introduzimos sequências e definimos o que significa para uma sequência convergir ou divergir. Mostramos como encontrar limites de sequências que convergem, geralmente usando as propriedades de limites para funções discutidas anteriormente. Fechamos esta seção com o Teorema da Convergência Monótona, uma ferramenta que podemos usar para provar que certos tipos de sequências convergem.

Terminologia de sequências

Para trabalhar com esse novo tópico, precisamos de alguns novos termos e definições. Primeiro, uma sequência infinita é uma lista ordenada de números do formulário

$$a_1,a_2,a_3,…,a_n,….\nonumber$$

Cada um dos números na sequência é chamado de termo. O símbolo$n$ é chamado de variável de índice da sequência. Usamos a notação

$$\{a_n\}^∞_{n=1},\nonumber$$

ou simplesmente$\{a_n\}$, para denotar essa sequência. Uma notação similar é usada para conjuntos, mas uma sequência é uma lista ordenada, enquanto um conjunto não é ordenado. Como$a_n$ existe um número específico para cada número inteiro positivo$n$, também podemos definir uma sequência como uma função cujo domínio é o conjunto de números inteiros positivos.

Vamos considerar a lista infinita e ordenada

$$2,4,8,16,32,….\nonumber$$

Essa é uma sequência na qual o primeiro, o segundo e o terceiro termos são dados por$a_1=2, a_2=4,$ e$a_3=8.$ Você provavelmente pode ver que os termos nessa sequência têm o seguinte padrão:

$$a_1=2^1,\,a_2=2^2,\,a_3=2^3,\,a_4=2^4 \text{ and } a_5=2^5.\nonumber$$

Supondo que esse padrão continue, podemos escrever o$n^{\text{th}}$ termo na sequência pela fórmula explícita.$a_n=2^n.$ Usando essa notação, podemos escrever essa sequência como

$$\{2^n\}^∞_{n=1}\nonumber$$

ou

$$\{2^n\}.\nonumber$$

Como alternativa, podemos descrever essa sequência de uma maneira diferente. Como cada termo é o dobro do termo anterior, essa sequência pode ser definida recursivamente expressando o$n^{\text{th}}$ termo$a_n$ em termos do termo anterior$a_{n−1}$. Em particular, podemos definir essa sequência como a sequência$\{a_n\}$ onde,$a_1=2$ e para todos$n≥2$, cada termo an é definido pela relação de recorrência

$$a_n=2a_{n−1}. \nonumber$$

Definição: sequência infinita

Uma sequência infinita$\{a_n\}$ é uma lista ordenada de números do formulário

$a_1,\,a_2,\,…,\,a_n,\,….$

O subscrito$n$ é chamado de variável de índice da sequência. Cada número$a_n$ é um termo da sequência. Às vezes, as sequências são definidas por fórmulas explícitas, nesse caso,$a_n=f(n)$ para alguma função$f(n)$ definida sobre os números inteiros positivos. Em outros casos, as sequências são definidas usando uma relação de recorrência. Em uma relação de recorrência, um termo (ou mais) da sequência é dado explicitamente e os termos subsequentes são definidos em termos de termos anteriores na sequência.

Observe que o índice não precisa começar em$n=1$, mas pode começar com outros números inteiros. Por exemplo, uma sequência dada pela fórmula explícita$a_n=f(n)$ poderia começar em; nesse caso$n=0$, a sequência seria

$$a_0,\,a_1,\,a_2,….\nonumber$$

Da mesma forma, para uma sequência definida por uma relação de recorrência, o termo$a_0$ pode ser dado explicitamente e os termos$a_n$ para$n≥1$ podem ser definidos em termos de$a_{n−1}$. Como uma sequência$\{a_n\}$ tem exatamente um valor para cada inteiro positivo$n$, ela pode ser descrita como uma função cujo domínio é o conjunto de números inteiros positivos. Como resultado, faz sentido discutir o gráfico de uma sequência. O gráfico de uma sequência$\{a_n\}$ consiste em todos os pontos$(n,a_n)$ para todos os números inteiros positivos n. A Figura mostra o gráfico de${2^n}$.

Figura$\PageIndex{1}$: Os pontos representados graficamente são um gráfico da sequência {$2^n$}.

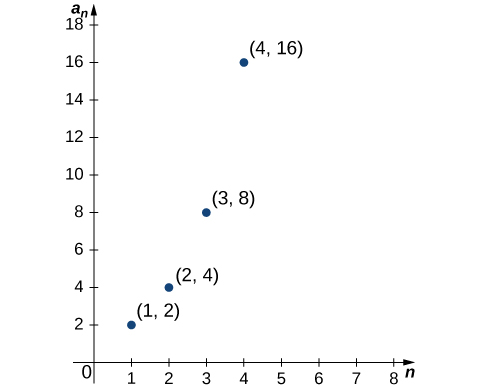
Dois tipos de sequências ocorrem com frequência e recebem nomes especiais: sequências aritméticas e sequências geométricas. Em uma sequência aritmética, a diferença entre cada par de termos consecutivos é a mesma. Por exemplo, considere a sequência

$$3,\,7,\,11,\,15,1\,9, \,\ldots\nonumber$$

Você pode ver que a diferença entre cada par consecutivo de termos é$4$. Supondo que esse padrão continue, essa sequência é uma sequência aritmética. Ela pode ser descrita usando a relação de recorrência

$$\begin{cases}a_1=3\\a_n=a_{n−1}+4, \text{ for }\ n≥2\end{cases}.\nonumber$$

Note que

$$a_2=3+4\nonumber$$

$$a_3=3+4+4=3+2⋅4\nonumber$$

$$a_4=3+4+4+4=3+3⋅4.\nonumber$$

Assim, a sequência também pode ser descrita usando a fórmula explícita.

$$a_n=3+4(n−1)=4n−1.\nonumber$$

Em geral, uma sequência aritmética é qualquer sequência da forma$a_n=cn+b.$

Em uma sequência geométrica, a proporção de cada par de termos consecutivos é a mesma. Por exemplo, considere a sequência

$$2,\,−\dfrac{2}{3},\,\dfrac{2}{9},\,−\dfrac{2}{27},\,\dfrac{2}{81},….\nonumber$$

Vemos que a proporção de qualquer termo em relação ao termo anterior é$−\dfrac{1}{3}$. Supondo que esse padrão continue, essa sequência é uma sequência geométrica. Pode ser definido recursivamente como

$$a_1=2\nonumber$$

$$a_n=−\dfrac{1}{3}⋅a_{n−1}, \text{ for }\ n≥2.\nonumber$$

Alternativamente, já que

$$\begin{align*} a_2 &=−\dfrac{1}{3}⋅2 \\[4pt] a_3 &=\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^2⋅2 \\[4pt] a_4 &= \left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^3⋅2,\end{align*} \nonumber$$

vemos que a sequência pode ser descrita usando a fórmula explícita

$$a_n=2 \left(−\dfrac{1}{3}\right)^{n−1}.\nonumber$$

A sequência$\{2^n\}$ que discutimos anteriormente é uma sequência geométrica, na qual a proporção de qualquer termo em relação ao termo anterior é$2$. Em geral, uma sequência geométrica é qualquer sequência do formulário$a_n=cr^n$.

Exemplo$\PageIndex{1}$: Finding Explicit Formulas

Para cada uma das sequências a seguir, encontre uma fórmula explícita para o$n^{\text{th}}$ termo da sequência.

1. $−\dfrac{1}{2},\dfrac{2}{3},−\dfrac{3}{4},\dfrac{4}{5},−\dfrac{5}{6},…$
2. $\dfrac{3}{4},\dfrac{9}{7},\dfrac{27}{10},\dfrac{81}{13},\dfrac{243}{16},…$.

Solução

a. Primeiro, observe que a sequência está alternando de negativo para positivo. Os termos ímpares na sequência são negativos e os termos pares são positivos. Portanto, o$n^{\text{th}}$ termo inclui um fator de$(−1)^n$. Em seguida, considere a sequência de numeradores${1,2,3,…}$ e a sequência de denominadores${2,3,4,…}$. Podemos ver que essas duas sequências são sequências aritméticas. O$n^{\text{th}}$ termo na sequência de numeradores é$n$, e o$n^{\text{th}}$ termo na sequência de denominadores é$n+1$. Portanto, a sequência pode ser descrita pela fórmula explícita

$$a_n=\dfrac{(−1)^nn}{n+1}. \nonumber$$

b. A sequência de numeradores$3,9,27,81,243,…$ é uma sequência geométrica. O numerador do$n^{\text{th}}$ termo é$3^n$ A sequência de denominadores$4,7,10,13,16,…$ é uma sequência aritmética. O denominador do$n^{\text{th}}$ termo é$4+3(n−1)=3n+1.$ Portanto, podemos descrever a sequência pela fórmula explícita$a_n=\dfrac{3^n}{3n+1.}$

Exercício$\PageIndex{1}$

Encontre uma fórmula explícita para o$n^{\text{th}}$ termo da sequência$\left\{\dfrac{1}{5},−\dfrac{1}{7},\dfrac{1}{9},−\dfrac{1}{11},…\right\}.$

Dica

Os denominadores formam uma sequência aritmética.

Resposta

$a_n=\dfrac{(−1)^{n+1}}{3+2n}$

Exemplo$\PageIndex{2}$: Defined by Recurrence Relations

Para cada uma das seguintes sequências definidas recursivamente, encontre uma fórmula explícita para a sequência.

1. $a_1=2, a_n=−3a_{n−1}$para$n≥2$
2. $a_1=\left(\dfrac{1}{2}\right), a_n=a_{n−1}+\left(\dfrac{1}{2}\right)^n$para$n≥2$

Solução

a. Escrevendo os primeiros termos, temos

$$\begin{align*} a_1 &=2 \\[4pt] a_2 &=−3a_1=−3(2)\\[4pt] a_3 &=−3a_2=(−3)^22\\[4pt] a_4 &=−3a_3=(−3)^32.\end{align*}$$

Em geral,

$a_n=2(−3)^{n−1}.$

b. Escreva os primeiros termos:

$a_1=\dfrac{1}{2}$

$a_2=a_1+\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}$

$a_3=a_2+\left(\dfrac{1}{2}\right)^3=\dfrac{3}{4}+\dfrac{1}{8}=\dfrac{7}{8}$

$a_4=a_3+\left(\dfrac{1}{2}\right)^4=\dfrac{7}{8}+\dfrac{1}{16}=\dfrac{15}{16}$.

A partir desse padrão, derivamos a fórmula explícita

$a_n=\dfrac{2^n−1}{2^n}=1−\dfrac{1}{2^n}$.

Exercício$\PageIndex{2}$

Encontre uma fórmula explícita para a sequência definida recursivamente de forma que$a_1=−4$$a_n=a_{n−1}+6$ e.

Dica

Essa é uma sequência aritmética.

Resposta

$a_n=6n−10$

Limite de uma sequência

Uma questão fundamental que surge em relação às sequências infinitas é o comportamento dos termos à$n$ medida que aumenta. Como uma sequência é uma função definida em números inteiros positivos, faz sentido discutir o limite dos termos como$n→∞$. Por exemplo, considere as quatro sequências a seguir e seus diferentes comportamentos como$n→∞$ (Figura$\PageIndex{2}$):

1. $\{1+3n\}=\{4,7,10,13,…\}.$Os termos$1+3n$ se tornam arbitrariamente grandes à medida que$n→∞$. Nesse caso, dizemos que$1+3n→∞$ como$n→∞.$
2. $\left\{1− \left(\dfrac{1}{2}\right) ^n\right\}=\left\{ \dfrac{1}{2} ,\dfrac{3}{4},\dfrac{7}{8},\dfrac{15}{16}\,…\right\}.$Os termos$1−\left(\dfrac{1}{2}\right)^n→1$ como$n→∞.$
3. $\{(−1)^n\}=\{−1,1,−1,1,…\}.$Os termos se alternam, mas não se aproximam de um único valor como$n→∞.$
4. $\left\{\dfrac{(−1)^n}{n}\right\}=\left\{−1,\dfrac{1}{2},−\dfrac{1}{3},\dfrac{1}{4},…\right\}.$Os termos também se alternam para essa sequência, mas$\dfrac{(−1)^n}{n}→0$ como$n→∞.$

Figura$\PageIndex{2}$: (a) Os termos na sequência se tornam arbitrariamente grandes como$n→∞$. (b) Os termos na sequência se aproximam$1$ como$n→∞$. (c) Os termos na sequência alternam entre$1$ e$−1$ como$n→∞$. (d) Os termos na sequência alternam entre valores positivos e negativos, mas se aproximam$0$ como$n→∞$.

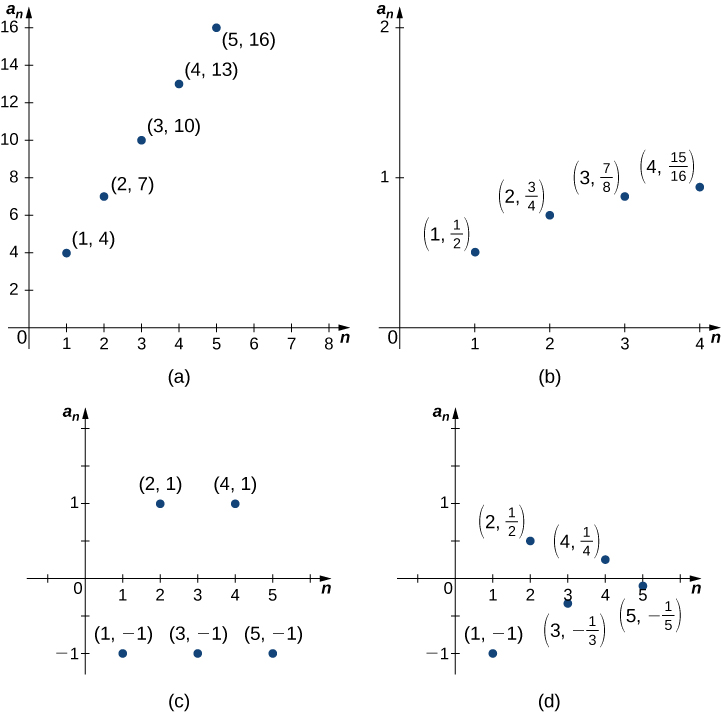
A partir desses exemplos, vemos várias possibilidades para o comportamento dos termos de uma sequência como$n→∞$. Em duas das sequências, os termos se aproximam de um número finito como$n→∞.$ Nas outras duas sequências, os termos não. Se os termos de uma sequência se aproximam de um número finito$L$ como$n→∞$, dizemos que a sequência é uma sequência convergente e o número real L é o limite da sequência. Podemos dar uma definição informal aqui.

Definição: sequências convergentes e divergentes

Dada uma sequência,${a_n},$ se os termos an se tornarem arbitrariamente próximos de um número finito à$L$ medida que n se torna suficientemente grande, dizemos que$\{a_n\}$ é uma sequência convergente e$L$ é o limite da sequência. Nesse caso, escrevemos

$$\lim_{n→∞}a_n=L. \nonumber$$

Se uma sequência não$\{a_n\}$ é convergente, dizemos que é uma sequência divergente.

Na Figura, vemos que os termos na sequência$\left\{1− \left(\dfrac{1}{2}\right)^n\right\}$ estão se tornando arbitrariamente próximos à$1$ medida que$n$ se torna muito grande. Concluímos que$\left\{1−\left(\dfrac{1}{2}\right)^n\right\}$ é uma sequência convergente e seu limite é$1$. Em contraste, na Figura, vemos que os termos na sequência não$1+3n$ estão se aproximando de um número finito à medida que$n$ se torna maior. Dizemos que$\{1+3n\}$ é uma sequência divergente.

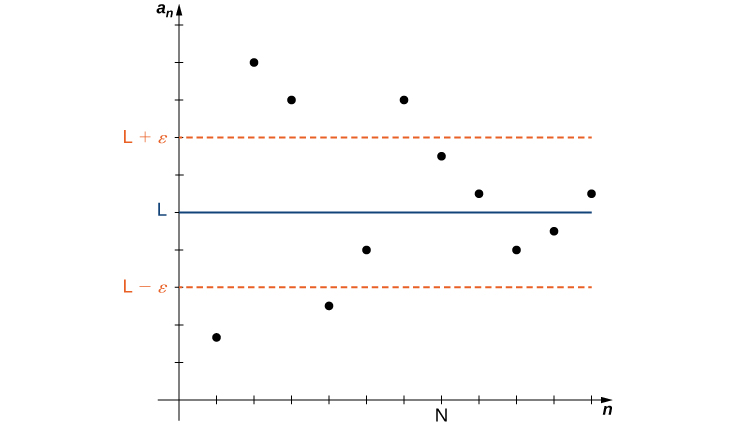
Na definição informal do limite de uma sequência, usamos os termos “arbitrariamente próximo” e “suficientemente grande”. Embora essas frases ajudem a ilustrar o significado de uma sequência convergente, elas são um tanto vagas. Para ser mais preciso, agora apresentamos a definição mais formal de limite para uma sequência e mostramos essas ideias graficamente na Figura.

Definição: Convergência

Uma sequência$\{a_n\}$ converge para um número real$L$ se$ε>0$, para todos, existir um inteiro$N$ igual ao de todos$n ≥ N$$|a_n−L| < ε$. O número$L$ é o limite da sequência e escrevemos

$$\lim_{n→∞}a_n = L \text{ or } a_n→L. \nonumber$$

Nesse caso, dizemos que a sequência$\{a_n\}$ é uma sequência convergente. Se uma sequência não converge, é uma sequência divergente e dizemos que o limite não existe.

Observamos que a convergência ou divergência de uma sequência$\{a_n\}$ depende apenas do que acontece com os termos$a_n$ como$n→∞$. Portanto, se um número finito de termos$b_1,b_2,…,b_N$ for colocado antes de$a_1$ criar uma nova sequência

$$b_1,\,b_2,\,…,\,b_N,\,a_1,\,a_2,\,…,\nonumber$$

essa nova sequência convergirá se$\{a_n\}$ convergir e divergirá se$\{a_n\}$ divergir. Além disso, se a sequência$\{a_n\}$ convergir para$L$, essa nova sequência também convergirá para$L$.

Figura$\PageIndex{3}$: À medida que$n$ aumenta, os termos$a_n$ se aproximam de$L$. Para valores de$n≥N$, a distância entre cada ponto$(n,a_n)$ e a linha$y=L$ é menor que$ε$.

Conforme definido acima, se uma sequência não convergir, é considerada uma sequência divergente. Por exemplo, as sequências$\{1+3n\}$ e$\left\{(−1)^n\right\}$ mostradas na Figura divergem. No entanto, sequências diferentes podem divergir de maneiras diferentes. A sequência$\left\{(−1)^n\right\}$ diverge porque os termos alternam entre$1$ e$−1$, mas não se aproximam de um valor como$n→∞$. Por outro lado, a sequência$\{1+3n\}$ diverge porque os termos$1+3n→∞$ como$n→∞$. Dizemos que a sequência$\{1+3n\}$ diverge até o infinito e escrevemos$\displaystyle \lim_{n→∞}(1+3n)=∞$. É importante reconhecer que essa notação não implica que o limite da sequência$\{1+3n\}$ exista. A sequência é, de fato, divergente. Escrever que o limite é infinito serve apenas para fornecer mais informações sobre por que a sequência é divergente. Uma sequência também pode divergir para o infinito negativo. Por exemplo, a sequência$\{−5n+2\}$ diverge para o infinito negativo porque$−5n+2→−∞$ como$n→−∞$. Nós escrevemos isso como$\displaystyle \lim_{n→∞}(−5n+2)=→−∞.$

Como uma sequência é uma função cujo domínio é o conjunto de números inteiros positivos, podemos usar propriedades de limites de funções para determinar se uma sequência converge. Por exemplo, considere uma sequência$\{a_n\}$ e uma função relacionada$f$ definidas em todos os números reais positivos, de forma que$f(n)=a_n$ para todos os números inteiros$n≥1$. Como o domínio da sequência é um subconjunto do domínio de$f$, se$\displaystyle \lim_{x→∞}f(x)$ existir, a sequência converge e tem o mesmo limite. Por exemplo, considere a sequência$\left\{\dfrac{1}{n}\right\}$ e a função relacionada$f(x)=\dfrac{1}{x}$. Como a função$f$ definida em todos os números reais$x>0$ satisfaz$f(x)=\dfrac{1}{x}→0$ como$x→∞$, a sequência$\left\{\dfrac{1}{n}\right\}$ deve satisfazer$\dfrac{1}{n}→0$ como$n→∞.$

Limite de uma sequência definida por uma função

Considere uma sequência$\{a_n\}$ como essa$a_n=f(n)$ para todos$n≥1$. Se existe um número real$L$ tal que

$$\lim_{x→∞}f(x)=L, \nonumber$$

então$\{a_n\}$ converge e

$$\lim_{n→∞}a_n=L. \nonumber$$

Podemos usar esse teorema$\displaystyle \lim_{n→∞}r^n$ para avaliar$0≤r≤1$. Por exemplo, considere a sequência$\left\{(1/2)^n\right\}$ e a função exponencial relacionada$f(x)=(1/2)^x$. Desde então$\displaystyle \lim_{x→∞}(1/2)^x=0$, concluímos que a sequência$\left\{(1/2)^n\right\}$ converge e seu limite é$0$. Da mesma forma, para qualquer número real$r$ como esse$0≤r<1$$\displaystyle \lim_{x→∞}r^x=0$, e, portanto, a sequência$\left\{r^n\right\}$ converge. Por outro lado, se$r=1$, então e$\displaystyle \lim_{x→∞}r^x=1$, portanto, o limite da sequência$\left\{1^n\right\}$ é$1$. Se$r>1$$\displaystyle \lim_{x→∞}r^x=∞$, e portanto, não podemos aplicar esse teorema. No entanto, nesse caso, assim como a função$r^x$ cresce sem limite como$n→∞$, os termos$r^n$ na sequência se tornam arbitrariamente grandes como$n→∞$, e concluímos que a sequência$\left\{r^n\right\}$ diverge para o infinito if$r>1$.

Resumimos esses resultados em relação à sequência geométrica${r^n}$:

$r^n→0$E se$0<r<1$

$r^n→1$E se$r=1$

$r^n→∞$E se$r>1$.

Posteriormente, nesta seção, consideraremos o caso de quando$r<0$.

Agora, consideramos sequências um pouco mais complicadas. Por exemplo, considere a sequência$\left\{(2/3)^n+(1/4)^n\right\}.$ Os termos nesta sequência são mais complicados do que outras sequências que discutimos, mas felizmente o limite dessa sequência é determinado pelos limites das duas sequências$\left\{(2/3)^n\right\}$$\left\{(1/4)^n\right\}$ e. Como descrevemos nas seguintes leis de limite algébricos, uma vez que$\left\{(2/3)^n\right\}$ e$\left\{1/4)^n\right\}$ ambas convergem para$0$, a sequência$\left\{(2/3)^n+(1/4)^n\right\}$ converge para$0+0=0$. Assim como pudemos calcular um limite envolvendo uma combinação algébrica de funções$f$ e$g$ observando os limites de$f$ e$g$ (veja Introdução aos Limites), somos capazes de avaliar o limite de uma sequência cujos termos são combinações algébricas de$a_n$ e $b_n$avaliando os limites de$\{a_n\}$$\{b_n\}$ e.

Leis de limite algébrico

Dadas sequências$\{a_n\}$$\{b_n\}$ e qualquer número real$c$, se existirem constantes$A$ e$B$ tal que$\displaystyle \lim_{n→∞}a_n=A$ e$\displaystyle \lim_{n→∞}b_n=B$, então

1. $\displaystyle \lim_{n→∞}c=c$
2. $\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA$
3. $\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B$
4. $\displaystyle \lim_{n→∞}(a_n⋅b_n)=\big(\lim_{n→∞}a_n\big)⋅\big(\lim_{n→∞}b_n\big)=A⋅B$
5. $\displaystyle \lim_{n→∞}\left(\dfrac{a_n}{b_n}\right)=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}=\dfrac{A}{B}$, fornecido$B≠0$ e cada$b_n≠0.$

Prova

Nós provamos a parte iii.

Deixe$ϵ>0$. Desde então$\displaystyle \lim_{n→∞}a_n=A$, existe um número inteiro positivo constante$N_1$, tal como para todos$n≥N_1$. Desde então$\displaystyle \lim_{n→∞}b_n=B$, existe uma constante$N_2$ tal que$|b_n−B|<ε/2$ para todos$n≥N_2$. $N$Seja o maior de$N_1$$N_2$ e. Portanto, para todos$n≥N$,$|(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{2}+\dfrac{ε}{2}=ε$.

□

As leis de limite algébricos nos permitem avaliar limites para muitas sequências. Por exemplo, considere a sequência$a_n={\dfrac{1}{n^2}}$. Conforme mostrado anteriormente,$\displaystyle \lim_{n→∞}\dfrac{1}{n}=0$. Da mesma forma, para qualquer número inteiro positivo$k$, podemos concluir que

$$\lim_{n→∞}\dfrac{1}{n^k}=0. \nonumber$$

No próximo exemplo, usamos esse fato junto com as leis de limite para avaliar limites para outras sequências.

Exemplo$\PageIndex{3}$: Determining Convergence and Finding Limits

Para cada uma das sequências a seguir, determine se a sequência converge ou não. Se ele convergir, encontre seu limite.

1. $\left\{5−\dfrac{3}{n^2}\right\}$
2. $\left\{\dfrac{3n^4−7n^2+5}{6−4n^4}\right\}$
3. $\left\{\dfrac{2^n}{n^2}\right\}$
4. $\left\{\left(1+\dfrac{4}{n}\right)^n\right\}$

Solução

a. Nós sabemos disso$\displaystyle \lim_{n→∞}\dfrac{1}{n}=0$. Usando esse fato, concluímos que

$\displaystyle \lim_{n→∞}\dfrac{1}{n^2}=\lim_{n→∞}\dfrac{1}{n}.\lim_{n→∞}\dfrac{1}{n}=0.$

Portanto,

$\displaystyle \lim_{n→∞}\left(5−\dfrac{3}{n^2}\right)=\lim_{n→∞}5−3\lim_{n→∞}\dfrac{1}{n^2}=5−3.0=5.$

A sequência converge e seu limite é 5.

b. Ao fatorar$n^4$ o numerador e o denominador e usar as leis de limite acima, temos

\ [\ begin {align*}\ lim_ {n→∞}\ dfrac {3n^4−7n^2+5} {6−4n^4} &=\ lim_ {n→∞}\ dfrac {3−\ dfrac {7} {n^2} +\ dfrac {5} {n^4}} {\ dfrac {6} {n^4}} {\ dfrac {6} {n^2} 4} −4}\\ [5pt]
&=\ dfrac {\ lim_ {n→∞} (3−\ dfrac {7} {n^2} +\ dfrac {5} {n^4})} {\ lim_ {n→∞} (\ dfrac {6} {n^4} −4)}\\ [5pt]
&=\ dfrac {\ lim_ {n→∞} (3) −\ lim_ {n→∞}\ dfrac {7} {n^2} +\ lim_ {n→∞}\ dfrac {5} {n^4}} {\ lim_ {n→∞}\ dfrac {6} {n^4} −\ lim_ {n→∞} (4)}\\ [5 pontos]
&=\ dfrac {\ lim_ {n→∞} (3) −7\ lim_ {n→∞}\ dfrac {1} {n^2} +5‣\ lim_ {n→∞}\ dfrac {1} {n^4}} {6\ lim_ {n→∞}\ dfrac {1} {n^4} −\ lim_ {n→∞} (4)}\\ [5pt]
&=\ dfrac {3−7⋅0+5⋅0} {6⋅0−4} =−\ dfrac {3} {4}. \ end {align*}\]

A sequência converge e seu limite é$−3/4$.

c. Considere a função relacionada$f(x)=2^x/x^2$ definida em todos os números reais$x>0$. Desde$2^x→∞$ e$x^2→∞$ como$x→∞$, aplique a regra de L'Hôpital e escreva

\ [\ begin {align*}\ lim_ {x→∞}\ dfrac {2^x} {x^2} &=\ lim_ {x→∞}\ dfrac {2^x\ ln2} {2x} & &\ text {Pegue as derivadas do numerador e do denominador.}\\ [5pt]
&=\ lim_ {x→∞}\ dfrac {2^x (\ ln2) ^2} {2} & &\ text {Pegue as derivadas novamente.}\\ [5pt]
&=∞. \ end {align*}\]

Concluímos que a sequência diverge.

d. Considere a função$f(x)=\left(1+\dfrac{4}{x}\right)^x$ definida em todos os números reais$x>0$. Esta função tem a forma indeterminada$1^∞$ como$x→∞.$ Let

$\displaystyle y=\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x$.

Agora, tomando o logaritmo natural de ambos os lados da equação, obtemos

$\displaystyle \ln(y)=\ln\left[\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\right]$.

Como a função$f(x)=\ln(x)$ é contínua em seu domínio, podemos trocar o limite e o logaritmo natural. Portanto,

$\displaystyle \ln(y)=\lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]$.

Usando propriedades de logaritmos, escrevemos

$\displaystyle \lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)$.

Como o lado direito dessa equação tem a forma indeterminada$∞⋅0$, reescreva-a como uma fração para aplicar a regra de L'Hôpital. Escreva

$\displaystyle \lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)=\lim_{x→∞}\dfrac{\ln\left(1+4/x\right)}{1/x}$.

Como o lado direito está agora na forma indeterminada 0/0, podemos aplicar a regra de L'Hôpital. Concluímos que

$\displaystyle \lim_{x→∞}\dfrac{\ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+4/x}=4.$

Portanto,$\ln(y)=4$$y=e^4$ e. Portanto, desde então$\displaystyle \lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x=e^4$, podemos concluir que a sequência$\left\{\left(1+\dfrac{4}{n}\right)^n\right\}$ converge para$e^4$.

Exercício$\PageIndex{3}$

Considere a sequência$\left\{(5n^2+1)/e^n\right\}.$ Determine se a sequência converge ou não. Se ele convergir, encontre seu limite.

Dica

Use a regra de L'Hôpital.

Resposta

A sequência converge e seu limite é$0$

Lembre-se de que se$f$ é uma função contínua em um valor$L$, então$f(x)→f(L)$ como$x→L$. Essa ideia também se aplica às sequências. Suponha que uma sequência$a_n→L$ e uma função$f$ seja contínua em$L$. Então$f(a_n)→f(L)$. Essa propriedade geralmente nos permite encontrar limites para sequências complicadas. Por exemplo, considere a sequência$\sqrt{5−\dfrac{3}{n^2}}$. Do exemplo a. conhecemos a sequência$5−\dfrac{3}{n^2}→5$. Uma vez que$\sqrt{x}$ é uma função contínua em$x=5$,

$$\lim_{n→∞}\sqrt{5−\dfrac{3}{n^2}}=\sqrt{\lim_{n→∞}(5−\dfrac{3}{n^2})}=\sqrt{5}.\nonumber$$

Funções contínuas definidas em sequências convergentes

Considere uma sequência$\{a_n\}$ e suponha que$L$ exista um número real para o qual a sequência$\{a_n\}$ converja$L$. Suponha que$f$ seja uma função contínua em$L$. Então, existe um número inteiro$N$ que$f$ é definido em todos os valores e for$n≥N$, e a sequência$\{f(a_n)\}$ converge para$f(L)$ (Figura$\PageIndex{4}$).

Figura$\PageIndex{4}$: Como$f$ é uma função contínua como$a_1,\,a_2,\,a_3,\,…$ abordagem de entradas$L$, a$f(a_1),\,f(a_2),\,f(a_3),\,…$ abordagem de saídas$f(L)$.

Prova

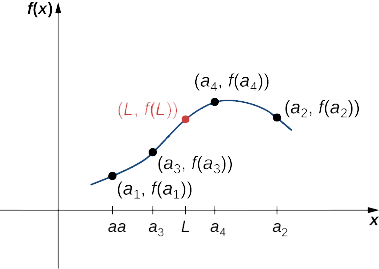
Let$ϵ>0.$ Since$f$ é contínuo em$L$, existe$δ>0$ tal que$|f(x)−f(L)|<ε$ se$|x−L|<δ$. Como a sequência$\{a_n\}$ converge para$L$,$N$ existe isso$|a_n−L|<δ$ para todos$n≥N$. Portanto, para todos$n≥N$$|a_n−L|<δ$, o que implica$|f(a_n)−f(L)|<ε$. Concluímos que a sequência$\{f(a_n)\}$ converge para$f(L)$.

□

Exemplo$\PageIndex{4}$: Limits Involving Continuous Functions Defined on Convergent Sequences

Determine se a sequência$\left\{\cos(3/n^2)\right\}$ converge. Se ele convergir, encontre seu limite.

Solução:

Como a sequência$\left\{3/n^2\right\}$ converge para$0$ e$\cos x$ é contínua em$x=0$, podemos concluir que a sequência$\left\{\cos(3/n^2)\right\}$ converge e

$\displaystyle \lim_{n→∞}\cos\left(\dfrac{3}{n^2}\right)=\cos 0=1.$

Exercício$\PageIndex{4}$

Determine se a sequência$\left\{\sqrt{\dfrac{2n+1}{3n+5}}\right\}$ converge. Se ele convergir, encontre seu limite.

Dica

Considere a sequência$\left\{\dfrac{2n+1}{3n+5}\right\}.$

Resposta

A sequência converge e seu limite é$\sqrt{2/3}$.

Outro teorema envolvendo limites de sequências é uma extensão do Teorema de Squeeze para limites discutidos em Introdução aos Limites.

Teorema de Squeeze para sequências

Considere as sequências$\{a_n\}, \, \{b_n\},$$\{c_n\}$ e. Suponha que exista um número inteiro$N$ tal que

$a_n≤b_n≤c_n$para todos$n≥N.$

Se existe um número real$L$ tal que

$$\lim_{n→∞}a_n=L=\lim_{n→∞}c_n, \nonumber$$

em seguida,$\{b_n\}$ converge e$\displaystyle \lim_{n→∞}b_n=L$ (Figura$\PageIndex{5}$).

Figura$\PageIndex{5}$: Cada termo bn satisfaz$a_n≤b_n≤c_n$ e as sequências$\{a_n\}$$\{c_n\}$ convergem para o mesmo limite, então a sequência também$\{b_n\}$ deve convergir para o mesmo limite.

Prova

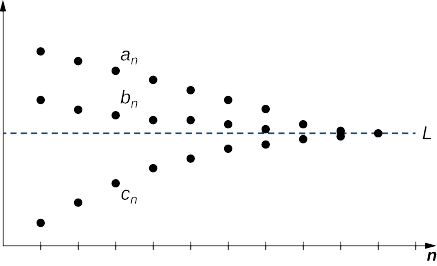
Let$ε>0.$ Como a sequência$\{a_n\}$ converge para$L$, existe um número inteiro$N_1$ igual ao$|a_n−L|<ε$ de todos$n≥N_1$. Da mesma forma, como$\{c_n\}$ converge para$L$, existe um número inteiro$N_2$ igual ao$|c_n−L|<ε$ de todos$n≥N_2$. Por suposição, existe um número inteiro$N$ igual ao$a_n≤b_n≤c_n$ de todos$n≥N$. $M$Seja o maior de$N_1,\, N_2$,$N$ e. Devemos mostrar isso$|b_n−L|<ε$ para todos$n≥M$. Para todos$n≥M$,

$$−ε<−|a_n−L|≤a_n−L≤b_n−L≤c_n−L≤|c_n−L|<ε\nonumber$$

Portanto,$−ε<b_n−L<ε,$ concluímos isso$|b_n−L|<ε$ para todos$n≥M$, e concluímos que a sequência${b_n}$ converge para$L$.

□

Exemplo$\PageIndex{5}$: Using the Squeeze Theorem

Use o Teorema de Squeeze para encontrar o limite de cada uma das seguintes sequências.

1. $\left\{\dfrac{\cos\, n}{n^2}\right\}$
2. $\left\{\left(−\dfrac{1}{2}\right)^n\right\}$

Solução

a. Uma vez que,$−1≤\cos n≤1$ para todos os números inteiros$n$, temos

$−\dfrac{1}{n^2} ≤ \dfrac{\cos n}{n^2}≤\dfrac{1}{n^2}.$

Desde$−1/n^2→0$ e$1/n^2→0$, concluímos isso$\cos n/n^2→0$ também.

b. Desde

$−\dfrac{1}{2^n} ≤ \left(−\dfrac{1}{2}\right)^n ≤ \dfrac{1}{2^n}$

para todos os números inteiros positivos$n, \, −1/2^n→0$ e$1/2^n→0,$ podemos concluir que$(−1/2)^n→0.$

Exercício$\PageIndex{5}$

Encontre$\displaystyle \lim_{n→∞}\dfrac{2n−\sin\, n}{n}.$

Dica

Use o fato de que$−1≤\sin n≤1.$

Resposta

$2$

Usando a ideia do Exemplo,$\PageIndex{5}$ b concluímos que$r^n→0$ para qualquer número real r tal que$−1<r<0.$ If$r<−1$, a sequência${r^n}$ diverge porque os termos oscilam e se tornam arbitrariamente grandes em magnitude. Se$r=−1$, a sequência${r^n}={(−1)^n}$ diverge, conforme discutido anteriormente. Aqui está um resumo das propriedades das sequências geométricas.

$r^n→0 \text{ if } |r|<1$

$r^n→1\text{ if } r=1$

$r^n→∞\text{ if } r>1$

$\left\{r^n\right\} \text{ diverges if } r≤−1$

Sequências limitadas

Agora voltamos nossa atenção para um dos teoremas mais importantes envolvendo sequências: o Teorema da Convergência Monótona. Antes de declarar o teorema, precisamos introduzir alguma terminologia e motivação. Começamos definindo o que significa delimitar uma sequência.

Definição: Sequências vinculadas

Uma sequência$\{a_n\}$ é limitada acima se existir um número real$M$ tal que

$a_n≤M$

para todos os números inteiros positivos$n$.

Uma sequência$\{a_n\}$ é limitada abaixo se existir um número real$m$ tal que

$m≤a_n$

para todos os números inteiros positivos$n$.

Uma sequência$\{a_n\}$ é uma sequência limitada se estiver limitada acima e limitada abaixo.

Se uma sequência não for limitada, ela será uma sequência ilimitada.

Por exemplo, a sequência$\{1/n\}$ está limitada acima porque$1/n≤1$ para todos os números inteiros positivos$n$. Também está limitado abaixo porque$1/n≥0$ para todos os números inteiros positivos$n$. Portanto,$\{1/n\}$ é uma sequência limitada. Por outro lado, considere a sequência$\left\{2^n\right\}$. Porque,$2^n≥2$ para todos$n≥1$, a sequência está limitada abaixo. No entanto, a sequência não está limitada acima. Portanto,$\left\{2^n\right\}$ é uma sequência ilimitada.

Agora discutimos a relação entre limite e convergência. Suponha que uma sequência$\{a_n\}$ seja ilimitada. Então, ele não está limitado acima, ou não está limitado abaixo, ou ambos. Em ambos os casos, existem termos e que são arbitrariamente grandes em magnitude à$n$ medida que aumentam. Como resultado, a sequência$\{a_n\}$ não pode convergir. Portanto, estar limitado é uma condição necessária para que uma sequência converja.

As sequências convergentes são limitadas

Se uma sequência$\{a_n\}$ convergir, ela será limitada.

Observe que uma sequência limitada não é uma condição suficiente para que uma sequência converja. Por exemplo, a sequência$\left\{(−1)^n\right\}$ é limitada, mas a sequência diverge porque a sequência oscila entre$1$ e$−1$ e nunca se aproxima de um número finito. Agora discutimos uma condição suficiente (mas não necessária) para que uma sequência limitada converja.

Considere uma sequência limitada$\{a_n\}$. Suponha que a sequência$\{a_n\}$ esteja aumentando. Ou seja,$a_1≤a_2≤a_3….$ como a sequência está aumentando, os termos não estão oscilando. Portanto, existem duas possibilidades. A sequência pode divergir para o infinito ou pode convergir. No entanto, como a sequência é limitada, ela é limitada acima e não pode divergir para o infinito. Concluímos que$\{a_n\}$ converge. Por exemplo, considere a sequência

$$\left\{\dfrac{1}{2},\,\dfrac{2}{3},\,\dfrac{3}{4},\,\dfrac{4}{5},\,…\right\}. \nonumber$$

Como essa sequência está aumentando e limitada acima, ela converge. Em seguida, considere a sequência

$$\left\{2,\,0,\,3,\,0,\,4,\,0,\,1,\,−\dfrac{1}{2},\,−\dfrac{1}{3},\,−\dfrac{1}{4},\,…\right\}. \nonumber$$

Mesmo que a sequência não esteja aumentando para todos os valores de$n$, vemos isso$−1/2<−1/3<−1/4<⋯$. Portanto, começando com o oitavo termo$a_8=−1/2$, a sequência está aumentando. Nesse caso, dizemos que a sequência está aumentando eventualmente. Como a sequência está limitada acima, ela converge. Também é verdade que, se uma sequência está diminuindo (ou eventualmente diminuindo) e limitada abaixo, ela também converge.

Definição

Uma sequência$\{a_n\}$ está aumentando para todos$n≥n_0$ se

$a_n≤a_{n+1}$para todos$n≥n_0$.

Uma sequência$\{a_n\}$ está diminuindo para todos$n≥n_0$ se

$a_n ≥ a_{n+1}$para todos$n≥n_0$.

Uma sequência$\{a_n\}$ é monótona para todos$n≥n_0$ se estiver aumentando para todos$n≥n_0$ ou diminuindo para todos$n≥n_0$.

Agora temos as definições necessárias para declarar o Teorema da Convergência Monótona, que fornece uma condição suficiente para a convergência de uma sequência.

Definição: Teorema da convergência monótona

Se$\{a_n\}$ for uma sequência limitada e existir um inteiro$n_0$ positivo que$\{a_n\}$ seja monótono para todos$n≥n_0$, então$\{a_n\}$ converge.

A prova desse teorema está além do escopo deste texto. Em vez disso, fornecemos um gráfico para mostrar intuitivamente por que esse teorema faz sentido (Figura$\PageIndex{6}$).

Figura$\PageIndex{6}$: Como a sequência$\{a_n\}$ está aumentando e limitada acima, ela deve convergir.

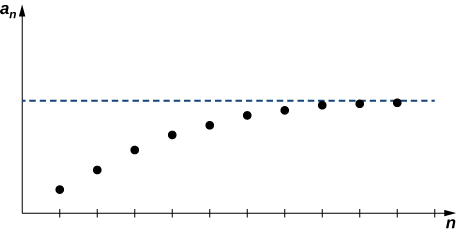
No exemplo a seguir, mostramos como o Teorema da Convergência Monótona pode ser usado para provar a convergência de uma sequência.

Exemplo$\PageIndex{6}$: Using the Monotone Convergence Theorem

Para cada uma das seguintes sequências, use o Teorema da Convergência Monótona para mostrar que a sequência converge e encontrar seu limite.

1. $\left\{\dfrac{4^n}{n!}\right\}$
2. $\{a_n\}$definido recursivamente de tal forma que
   
   $a_1=2$ e$a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}$ para todos$n≥2.$

Solução

a. Escrevendo os primeiros termos, vemos que

$\left\{\dfrac{4^n}{n!}\right\}=\left\{4,\,8,\,\dfrac{32}{3},\,\dfrac{32}{3},\,\dfrac{128}{15},\,…\right\}.$

No início, os termos aumentam. No entanto, após o terceiro mandato, os termos diminuem. Na verdade, os termos diminuem para todos$n≥3$. Podemos mostrar isso da seguinte forma.

$a_{n+1}=\dfrac{4^{n+1}}{(n+1)!}=\dfrac{4}{n+1}⋅\dfrac{4^n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n$E se$n≥3.$

Portanto, a sequência está diminuindo para todos$n≥3$. Além disso, a sequência é limitada abaixo por$0$ porque$4n/n!≥0$ para todos os números inteiros positivos$n$. Portanto, pelo Teorema da Convergência Monótona, a sequência converge.

Para encontrar o limite, usamos o fato de que a sequência converge e deixa$\displaystyle L=\lim_{n→∞}a_n$. Agora, observe essa observação importante. Considere$\displaystyle \lim_{n→∞}a_{n+1}$. Desde

$\{a_{n+1}\}=\{a_2,\,a_3,\,a_4,\,…\},$

a única diferença entre as sequências$\{a_{n+1}\}$ e$\{a_n\}$ é que$\{a_{n+1}\}$ omite o primeiro termo. Como um número finito de termos não afeta a convergência de uma sequência,

$\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}a_n=L.$

Combinando esse fato com a equação

$a_{n+1}=\dfrac{4}{n+1}a_n$

e tomando o limite de ambos os lados da equação

$\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}\dfrac{4}{n+1}a_n$,

podemos concluir que

$L=0⋅L=0.$

b. Escrevendo os primeiros termos,

$\left\{2,\,\dfrac{5}{4},\,\dfrac{41}{40},\,\dfrac{3281}{3280},\,…\right\}.$

podemos conjecturar que a sequência está diminuindo e limitada abaixo por$1$. Para mostrar que a sequência é limitada abaixo por$1$, podemos mostrar que

$\dfrac{a_n}{2}+\dfrac{1}{2a_n}≥1.$

Para mostrar isso, primeiro reescreva

$\dfrac{a_n}{2}+\dfrac{1}{2a_n}=\dfrac{a^2_n+1}{2a_n}$.

Uma vez que$a_1>0$ e$a_2$ é definido como uma soma de termos positivos, da$a_2>0.$ mesma forma, todos os termos$a_n>0$. Portanto,

$\dfrac{a^2n+1}{2a_n}≥1$

se e somente se

$a^2_n+1≥2a_n$.

Reescrevendo a desigualdade$a^2_n+1≥2a_n$ como$a^2_n−2a_n+1≥0$, e usando o fato de que

$a^2_n−2a_n+1=(a_n−1)^2≥0$

porque o quadrado de qualquer número real não é negativo, podemos concluir que

$\dfrac{a^n}{2}+\dfrac{1}{2a_n}≥1.$

Para mostrar que a sequência está diminuindo, devemos mostrar isso$a_{n+1}≤a_n$ para todos$n≥1$. Uma vez que$1≤a^2_n$, segue-se que

$a^2_n+1≤2a^2_n$.

Dividindo os dois lados por$2a_n$, obtemos

$\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.$

Usando a definição de$a_{n+1}$, concluímos que

$a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n$.

Como$\{a_n\}$ é limitado abaixo e decrescente, pelo Teorema da Convergência Monótona, ele converge.

Para encontrar o limite, deixe$\displaystyle L=\lim_{n→∞}a_n$. Em seguida, usando a relação de recorrência e o fato$\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}$ de que temos

$\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}(\dfrac{a_n}{2}+\dfrac{1}{2a_n})$,

e, portanto,

$L=\dfrac{L}{2}+\dfrac{1}{2L}$.

Multiplicando os dois lados dessa equação por$2L$, chegamos à equação

$2L^2=L^2+1$.

Resolvendo essa equação,$L,$ concluímos que$L^2=1$, o que implica$L=±1$. Como todos os termos são positivos, o limite$L=1$.

Exercício$\PageIndex{6}$

Considere a sequência$\{a_n\}$ definida recursivamente de forma que$a_1=1$,$a_n=a_{n−1}/2$. Use o Teorema da Convergência Monótona para mostrar que essa sequência converge e encontra seu limite.

Dica

Mostra que a sequência está diminuindo e delimitada abaixo.

Resposta

$0$.

Definição: Números de Fibonacci

Os números de Fibonacci são definidos recursivamente pela sequência$\left\{F_n\right\}$ onde$F_0=0, \, F_1=1$ e para$n≥2,$

$F_n=F_{n−1}+F_{n−2}.$

Aqui, examinamos as propriedades dos números de Fibonacci.

1. Escreva os primeiros vinte números de Fibonacci.

2. Encontre uma fórmula fechada para a sequência de Fibonacci usando as etapas a seguir.

a. Considere a sequência recursivamente definida${x_n}$ onde$x_0=c$$x_{n+1}=ax_n$ e. Mostre que essa sequência pode ser descrita pela fórmula fechada$x_n=ca^n$ para todos$n≥0.$

b. Usando o resultado da parte a. como motivação, procure uma solução da equação

$F_n=F_{n−1}+F_{n−2}$

do formulário$F_n=cλ^n$. Determine quais dois valores$λ$ permitirão$F_n$ satisfazer essa equação.

c. Considere as duas soluções da parte b.:$λ_1$$λ_2$ e. Deixe$F_n=c_1λ_1^n+c_2λ_2^n$. Use as condições iniciais$F_0$ e$F_1$ determine os valores das constantes$c_1$$c_2$ e escreva a fórmula fechada$F_n$.

3. Use a resposta em 2 c. para mostrar que

$$\lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\nonumber$$

O número$ϕ=(1+\sqrt{5})/2$ é conhecido como proporção áurea (Figura e Figura).

Figura$\PageIndex{7}$: As sementes de um girassol exibem padrões espirais curvados para a esquerda e para a direita. O número de espirais em cada direção é sempre um número de Fibonacci — sempre. (crédito: modificação do trabalho de Esdras Calderan, Wikimedia Commons)

Figura$\PageIndex{8}$: A proporção da proporção áurea aparece em muitos exemplos famosos de arte e arquitetura. O antigo templo grego conhecido como Partenon foi projetado com essas proporções, e a proporção aparece novamente em muitos dos detalhes menores. (crédito: modificação do trabalho da TravelingOtter, Flickr).

Conceitos-chave

• Para determinar a convergência de uma sequência dada por uma fórmula explícita$a_n=f(n)$, usamos as propriedades de limites para funções.
• Se$\{a_n\}$ e$\{b_n\}$ são sequências convergentes que convergem para$A$ e$B,$ respectivamente, e$c$ são qualquer número real, então a sequência$\{ca_n\}$ converge para$c\cdot A,$ as sequências$\{a_n±b_n\}$ convergem para$A±B,$ a sequência$\{a_n\cdot b_n\}$ converge para$A⋅B,$ e a a sequência$\{a_n/b_n\}$ converge para a$A/B,$ fornecida$B≠0.$
• Se uma sequência é limitada e monótona, ela converge, mas nem todas as sequências convergentes são monótonas.
• Se uma sequência é ilimitada, ela diverge, mas nem todas as sequências divergentes são ilimitadas.
• A sequência geométrica$\left\{r^n\right\}$ converge se e somente se$|r|<1$ ou$r=1$.

Glossário

sequência aritmética

uma sequência na qual a diferença entre cada par de termos consecutivos é a mesma é chamada de sequência aritmética

limitado acima

uma sequência$\{a_n\}$ é limitada acima se existir uma constante$M$ tal que$a_n≤M$ para todos os números inteiros positivos$n$

limitado abaixo

uma sequência$\{a_n\}$ é limitada abaixo se existir uma constante$M$ tal que$M≤a_n$ para todos os números inteiros positivos$n$

sequência limitada

uma sequência$\{a_n\}$ é limitada se existir uma constante$M$ tal que$|a_n|≤M$ para todos os números inteiros positivos$n$

sequência convergente

uma sequência convergente é uma sequência$\{a_n\}$ para a qual existe um número real$L$ tal que$a_n$ é arbitrariamente próximo do tempo que$n$ seja suficientemente grande$L$

sequência divergente

uma sequência que não é convergente é divergente

fórmula explícita

uma sequência pode ser definida por uma fórmula explícita tal que$a_n=f(n)$

sequência geométrica

uma sequência$\{a_n\}$ na qual a razão$a_{n+1}/a_n$ é a mesma para todos os números inteiros positivos$n$ é chamada de sequência geométrica

variável de índice

o subscrito usado para definir os termos em uma sequência é chamado de índice

limite de uma sequência

o número real$L$ para o qual uma sequência converge é chamado de limite da sequência

sequência monótona

uma sequência crescente ou decrescente

relação de recorrência

uma relação de recorrência é uma relação na qual um termo$a_n$ em uma sequência é definido em termos de termos anteriores na sequência

sequência

uma lista ordenada de números do formulário$a_1,\,a_2,\,a_3,\,…$ é uma sequência

prazo

o número$a_n$ na sequência$\{a_n\}$ é chamado de$n^{\text{th}}$ termo da sequência

sequência ilimitada

uma sequência que não é limitada é chamada de ilimitada