Skip to main content
Global

8.4E: Exercícios para a Seção 8.4

  1. Last updated
  2. Save as PDF
  • Page ID
    188042

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Modelo logístico básico

    Para os problemas 1 a 11, considere a equação logística na forma\( P'=CP−P^2.\) Desenhe o campo direcional e encontre a estabilidade dos equilíbrios.

    1)\( C=3\)

    2)\( C=0\)

    Resposta

    \( P=0\)semi-estável

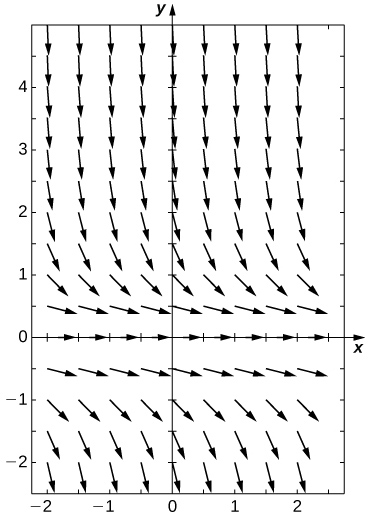
    3)\( C=−3\)

    4) Resolva a equação logística\( C=10\) e uma condição inicial de\( P(0)=2.\)

    Resposta
    \( P=\dfrac{10e^{10x}}{e^{10x}+4}\)

    5) Resolva a equação logística\( C=−10\) e uma condição inicial de\( P(0)=2\).

    6) Uma população de veados dentro de um parque tem uma capacidade de carga\( 200\) e uma taxa de crescimento de\( 2%\). Se a população inicial for de\( 50\) veados, qual é a população de veados em um determinado momento?

    Resposta
    \( P(t)=\dfrac{10000e^{0.02t}}{150+50e^{0.02t}}\)

    7) Uma população de sapos em um lago tem uma taxa de crescimento de\( 5%.\) Se a população inicial for de\( 1000\) sapos e a capacidade de carga for\( 6000\), qual é a população de sapos em um determinado momento?

    8) [T] As bactérias crescem a uma taxa de\( 20%\) por hora em uma placa de Petri. Se houver inicialmente uma bactéria e uma capacidade de carga de\( 1\) milhões de células, quanto tempo leva para chegar às\( 500,000\) células?

    Resposta
    \( 69\)horas\( 5\) minutos

    9) [T] Os coelhos em um parque têm uma população inicial de\( 10\) e crescem a uma taxa de\( 4%\) por ano. Se a capacidade de carga for\( 500\), a que horas a população chega aos\( 100\) coelhos?

    10) [T] Dois macacos são colocados em uma ilha. Depois de\( 5\) anos, existem\( 8\) macacos e a capacidade de carga estimada é de\( 25\) macacos. Quando a população de macacos chega aos\( 16\) macacos?

    Resposta
    \( 8\)anos\( 11\) meses

    11) [T] Um santuário de borboletas é construído para conter\( 2000\) borboletas, e as\( 400\) borboletas são inicialmente transferidas para dentro. Se depois de\( 2\) meses já existem\( 800\) borboletas, quando a população fica com\( 1500\) borboletas?

    Modelo logístico de população com esgotamento

    Os problemas a seguir consideram a equação logística com um termo adicional para esgotamento, seja por morte ou emigração.

    12) [T] A população de trutas em um lago é dada por\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−400\), onde as\( 400\) trutas são capturadas por ano. Use sua calculadora ou software de computador para desenhar um campo direcional e desenhar alguns exemplos de soluções. O que você espera do comportamento?

    Resposta

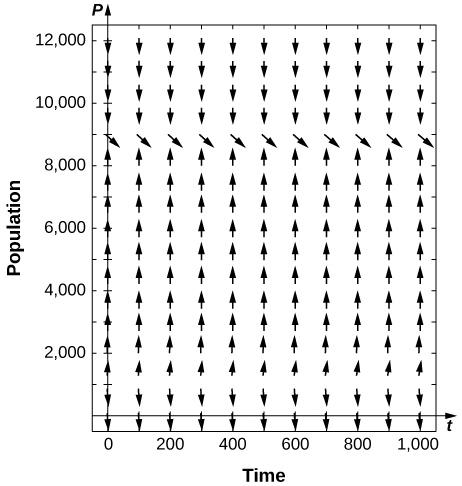
    13) No problema anterior, quais são as estabilidades dos equilíbrios\( 0<P_1<P_2\)?

    14) [T] Para o problema anterior, use o software para gerar um campo direcional para o valor\( f=400\). Quais são as estabilidades dos equilíbrios?

    Resposta

    \( P_1\)semi-estável

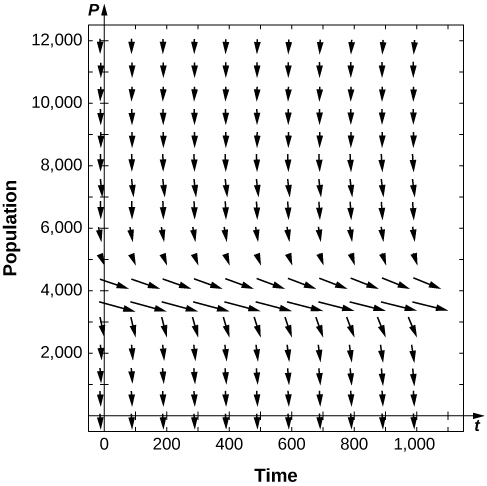
    15) [T] Para os problemas anteriores, use o software para gerar um campo direcional para o valor\( f=600.\) Quais são as estabilidades dos equilíbrios?

    16) [T] Para os problemas anteriores, considere o caso em que um certo número de peixes é adicionado ao tanque, ou\( f=−200.\) Quais são os equilíbrios não negativos e suas estabilidades?

    Resposta

    \( P_2>0\)estável

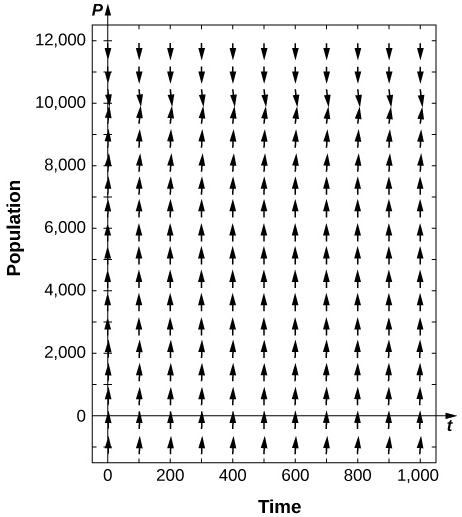
    É mais provável que a quantidade de pesca seja governada pelo número atual de peixes presentes, portanto, em vez de um número constante de peixes capturados, a taxa é proporcional ao número atual de peixes presentes, com proporcionalidade constante\( k\), como\( P'=0.4P\left(1−\dfrac{P}{10000}\right)−kP.\)

    17) [T] Para o problema de pesca anterior, desenhe um campo direcional assumindo\( k=0.1\). Desenhe algumas soluções que mostrem esse comportamento. Quais são os equilíbrios e quais são suas estabilidades?

    18) [T] Use um software ou uma calculadora para desenhar campos direcionais para\( k=0.4\). Quais são os equilíbrios não negativos e suas estabilidades?

    Resposta

    \( P_1=0\)é semi-estável

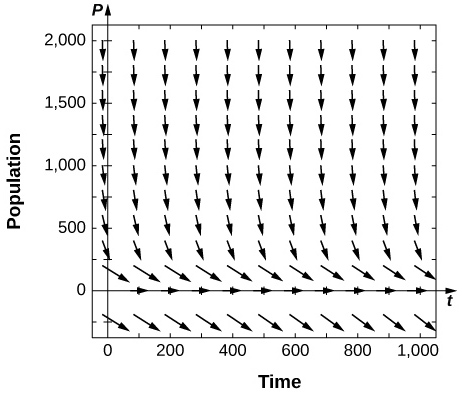
    19) [T] Use um software ou uma calculadora para desenhar campos direcionais para\( k=0.6\). Quais são os equilíbrios e suas estabilidades?

    20) Resolva esta equação, assumindo um valor de\( k=0.05\) e uma condição inicial de\( 2000\) peixe.

    Resposta
    \( y=\dfrac{−20}{4×10^{−6}−0.002e^{0.01t}}\)

    21) Resolva esta equação, assumindo um valor de\( k=0.05\) e uma condição inicial de\( 5000\) peixe.

    Limites mínimos de população sustentável

    Os problemas a seguir adicionam um valor limite mínimo para a sobrevivência da espécie,\( T\), que altera a equação diferencial para\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\).

    22) Desenhe o campo direcional da equação logística de limite, assumindo\( K=10,r=0.1,T=2\). Quando a população sobrevive? Quando é extinto?

    Resposta

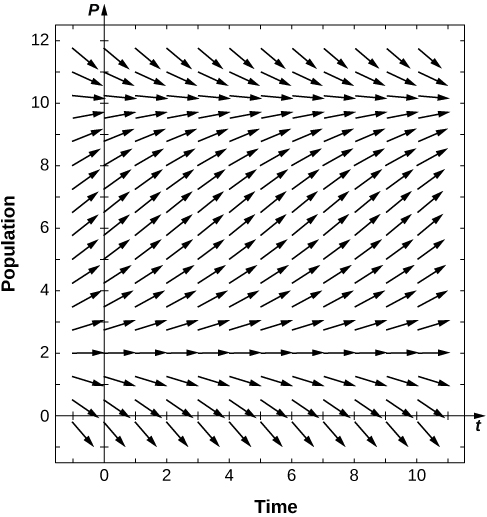
    23) Para o problema anterior, resolva a equação do limite logístico, assumindo a condição inicial\( P(0)=P_0\).

    24) Os tigres de Bengala em um parque de conservação têm uma capacidade de carga\( 100\) e precisam de um mínimo de\( 10\) para sobreviver. Se eles crescerem em população a uma taxa de\( 1%\) por ano, com uma população inicial de\( 15\) tigres, resolva o número de tigres presentes.

    Resposta
    \( P(t)=\dfrac{850+500e^{0.009t}}{85+5e^{0.009t}}\)

    25) Uma floresta contendo lêmures de cauda anelada em Madagascar tem o potencial de sustentar\( 5000\) indivíduos, e a população de lêmures cresce a uma taxa de\( 5%\) por ano. É necessário um mínimo de 500 indivíduos para que os lêmures sobrevivam. Dada uma população inicial de\( 600\) lêmures, resolva a população de lêmures.

    26) A população de leões da montanha no norte do Arizona tem uma capacidade de carga estimada\( 250\) e cresce a uma taxa de\( 0.25%\) por ano, e deve existir\( 25\) para que a população sobreviva. Com uma população inicial de leões da\( 30\) montanha, quantos anos serão necessários para tirar os leões da montanha da lista de espécies ameaçadas de extinção (pelo menos\( 100\))?

    Resposta
    \( 13\)anos meses

    A equação de Gompertz

    As perguntas a seguir consideram a equação de Gompertz, uma modificação para o crescimento logístico, que é frequentemente usada para modelar o crescimento do câncer, especificamente o número de células tumorais.

    27) A equação de Gompertz é dada por\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t).\) Desenhe os campos direcionais para esta equação assumindo que todos os parâmetros são positivos, e dado que\( K=1.\)

    28) Suponha que para uma população,\( K=1000\)\( α=0.05\) e. Desenhe o campo direcional associado a essa equação diferencial e desenhe algumas soluções. Qual é o comportamento da população?

    Resposta

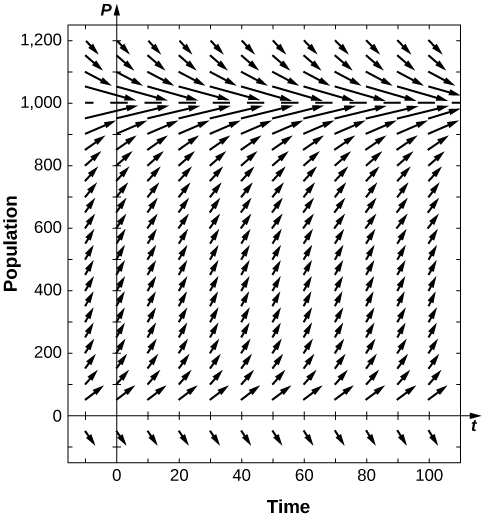
    29) Resolva a equação de Gompertz para genéricos\( α\)\( K\) e\( P(0)=P_0\) e.

    30) [T] A equação de Gompertz tem sido usada para modelar o crescimento do tumor no corpo humano. Partindo de uma célula tumoral no dia\( 1\)\( α=0.1\) e assumindo uma capacidade de carga de\( 10\) milhões de células, quanto tempo leva para atingir o estágio de “detecção” em\( 5\) milhões de células?

    Resposta
    \( 31.465\)dias

    31) [T] Estima-se que a população humana mundial atingiu\( 3\) bilhões de pessoas\( 1959\) e\( 6\) bilhões em\( 1999\). Assumindo uma capacidade de carga de\( 16\) bilhões de humanos, escreva e resolva a equação diferencial para o crescimento logístico e determine em que ano a população atingiu\( 7\) bilhões.

    32) [T] Estima-se que a população humana mundial atingiu\( 3\) bilhões de pessoas\( 1959\) e\( 6\) bilhões em\( 1999\). Assumindo uma capacidade de carga de\( 16\) bilhões de humanos, escreva e resolva a equação diferencial para o crescimento de Gompertz e determine em que ano a população atingiu\( 7\) bilhões. O crescimento logístico ou o crescimento de Gompertz foram mais precisos, considerando que a população mundial atingiu\( 7\) bilhões em outubro\( 31,2011?\)

    Resposta
    setembro\( 2008\)

    33) Mostre que a população cresce mais rápido quando atinge a metade da capacidade de carga da equação logística\( P'=rP\left(1−\dfrac{P}{K}\right)\).

    34) Quando a população aumenta mais rapidamente na equação logística de limite\( P'(t)=rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{T}{P}\right)\)?

    Resposta
    \( \dfrac{K+T}{2}\)

    35) Quando a população aumenta mais rapidamente para a equação de Gompertz\( P(t)'=α\ln\left(\frac{K}{P(t)}\right)P(t)?\)

    Abaixo está uma tabela das populações de guindastes na natureza\( 1940\) de\( 2000\) a. A população se recuperou da quase extinção após o início dos esforços de conservação. Os problemas a seguir consideram a aplicação de modelos populacionais para ajustar os dados. Suponha uma capacidade de carga de\( 10,000\) guindastes. Ajuste os dados supondo anos desde então\( 1940\) (então sua população inicial na época\( 0\) seria de\( 22\) guindastes).

    Ano (anos desde o início da conservação) População de guindastes
    1940 (0) 22
    1950 (10) 31
    1960 (20) 36
    1970 (30) 57
    1980 (40) 91
    1990 (50) 159
    2000 (60) 256

    Fonte: https://www.savingcranes.org/images/...wc_numbers.pdf

    36) Encontre a equação e o parâmetro\( r\) que melhor se ajustam aos dados da equação logística.

    Resposta
    \( r=0.0405\)

    37) Encontre a equação\( r\) e os parâmetros\( T\) que melhor se ajustam aos dados da equação logística de limite.

    38) Encontre a equação e o parâmetro\( α\) que melhor se ajustam aos dados da equação de Gompertz.

    Resposta
    \( α=0.0081\)

    39) Representar graficamente todas as três soluções e os dados no mesmo gráfico. Qual modelo parece ser mais preciso?

    40) Usando as três equações encontradas nos problemas anteriores, estime a população em\( 2010\) (ano\( 70\) após a conservação). A população real medida naquela época era\( 437\). Qual modelo é mais preciso?

    Resposta
    Logística:\( 361\), Limite:\( 436\), Gompertz:\( 309\).