8.4: A equação logística

Last updated
Save as PDF

Page ID: 188031

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Descreva o conceito de capacidade de carga ambiental no modelo logístico de crescimento populacional.
Desenhe um campo de direção para uma equação logística e interprete as curvas da solução.
Resolva uma equação logística e interprete os resultados.

Equações diferenciais podem ser usadas para representar o tamanho de uma população, pois ela varia ao longo do tempo. Vimos isso em um capítulo anterior na seção sobre crescimento e decaimento exponenciais, que é o modelo mais simples. Um modelo mais realista inclui outros fatores que afetam o crescimento da população. Nesta seção, estudamos a equação diferencial logística e vemos como ela se aplica ao estudo da dinâmica populacional no contexto da biologia.

Crescimento populacional e capacidade de carga

Para modelar o crescimento populacional usando uma equação diferencial, primeiro precisamos introduzir algumas variáveis e termos relevantes. A$t$ variável. representará o tempo. As unidades de tempo podem ser horas, dias, semanas, meses ou até anos. Qualquer problema específico deve especificar as unidades usadas nesse problema específico. A variável$P$ representará a população. Como a população varia com o tempo, ela é entendida como uma função do tempo. Portanto, usamos a notação$P(t)$ para a população em função do tempo. Se$P(t)$ for uma função diferenciável, a primeira derivada$\frac{dP}{dt}$ representa a taxa instantânea de variação da população em função do tempo.

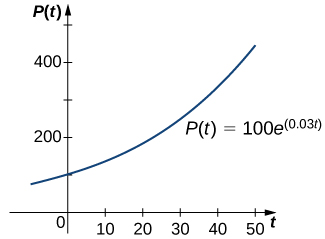
Em Crescimento e Decaimento Exponenciais, estudamos o crescimento exponencial e a decadência de populações e substâncias radioativas. Um exemplo de uma função de crescimento exponencial é$P(t)=P_0e^{rt}.$ Nesta função,$P(t)$ representa a população ao mesmo tempo$t,P_0$ representa a população inicial (população no momento$t=0$), e a constante$r>0$ é chamada de taxa de crescimento. A figura$\PageIndex{1}$ mostra um gráfico de$P(t)=100e^{0.03t}$. Aqui$P_0=100$$r=0.03$ e.

Um gráfico de uma função exponencial p (t) = 100 e ^ (0,03 t). É uma função ascendente côncava crescente começando no quadrante 2, cruza o eixo y em (0, 100) e aumenta no quadrante 1. — Figura$\PageIndex{1}$: Um modelo de crescimento exponencial da população.

Podemos verificar se a função$P(t)=P_0e^{rt}$ satisfaz o problema do valor inicial

\[ \dfrac{dP}{dt}=rP \nonumber \]

com$P(0)=P_0.$

Essa equação diferencial tem uma interpretação interessante. O lado esquerdo representa a taxa na qual a população aumenta (ou diminui). O lado direito é igual a uma constante positiva multiplicada pela população atual. Portanto, a equação diferencial afirma que a taxa na qual a população aumenta é proporcional à população naquele momento. Além disso, afirma que a constante de proporcionalidade nunca muda.

Um problema com essa função é a previsão de que, com o passar do tempo, a população cresce sem limites. Isso não é realista em um ambiente do mundo real. Vários fatores limitam a taxa de crescimento de uma determinada população, incluindo taxa de natalidade, taxa de mortalidade, suprimento de alimentos, predadores e assim por diante. A constante de crescimento$r$ geralmente leva em consideração as taxas de natalidade e mortalidade, mas nenhum dos outros fatores, e pode ser interpretada como uma taxa de crescimento percentual líquida (nascimento menos morte) por unidade de tempo. Uma pergunta natural a ser feita é se a taxa de crescimento populacional permanece constante ou se muda com o tempo. Biólogos descobriram que em muitos sistemas biológicos, a população cresce até que uma determinada população em estado estacionário seja atingida. Essa possibilidade não é levada em consideração no crescimento exponencial. No entanto, o conceito de capacidade de carga permite a possibilidade de que, em uma determinada área, apenas um certo número de um determinado organismo ou animal possa prosperar sem ter problemas de recursos.

Definição: Capacidade de transporte

A capacidade de carga de um organismo em um determinado ambiente é definida como a população máxima desse organismo que o meio ambiente pode sustentar indefinidamente.

Usamos a variável$K$ para indicar a capacidade de carga. A taxa de crescimento é representada pela variável$r$. Usando essas variáveis, podemos definir a equação diferencial logística.

Definição: Equação diferencial logística

Vamos$K$ representar a capacidade de carga de um determinado organismo em um determinado ambiente e$r$ ser um número real que represente a taxa de crescimento. A função$P(t)$ representa a população desse organismo em função do tempo$t$, e a constante$P_0$ representa a população inicial (população do organismo no momento$t=0$). Então, a equação diferencial logística é

\[\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right). \label{LogisticDiffEq} \]

A equação logística foi publicada pela primeira vez por Pierre Verhulst em$1845$. Essa equação diferencial pode ser acoplada à condição inicial$P(0)=P_0$ para formar um problema de valor inicial para$P(t).$

Suponha que a população inicial seja pequena em relação à capacidade de carga. Então$\frac{P}{K}$ é pequeno, possivelmente próximo de zero. Assim, a quantidade entre parênteses no lado direito da Equação\ ref {logisticDiffEq} está próxima de$1$, e o lado direito dessa equação está próximo de$rP$. Se$r>0$, então a população cresce rapidamente, semelhante ao crescimento exponencial.

No entanto, à medida que a população cresce, a proporção$\frac{P}{K}$ também cresce, porque$K$ é constante. Se a população permanecer abaixo da capacidade de carga, então$\frac{P}{K}$ é menor que$1$, então$1−\frac{P}{K}>0$. Portanto, o lado direito da Equação\ ref {logisticDiffEq} ainda é positivo, mas a quantidade entre parênteses fica menor e a taxa de crescimento diminui como resultado. Se$P=K$ então, o lado direito é igual a zero e a população não muda.

Agora, suponha que a população comece com um valor maior do que a capacidade de carga. Em seguida$\frac{P}{K}>1,$,$1−\frac{P}{K}<0$ e. Então, o lado direito da Equação\ ref {logisticDiffEq} é negativo e a população diminui. Enquanto isso$P>K$, a população diminui. Na verdade, nunca atinge K porque$\frac{dP}{dt}$ ficará cada vez menor, mas a população se aproxima da capacidade de carga quando$t$ se aproxima do infinito. Essa análise pode ser representada visualmente por meio de uma linha de fase. Uma linha de fase descreve o comportamento geral de uma solução para uma equação diferencial autônoma, dependendo da condição inicial. Para o caso de uma capacidade de carga na equação logística, a linha de fase é mostrada na Figura$\PageIndex{2}$.

Um diagrama da linha de fase para a equação diferencial dada. Uma linha azul vertical com setas em cada extremidade tem dois pontos marcados, em P = K e P = 0, com K — Figura$\PageIndex{2}$: Uma linha de fase para a equação diferencial$\dfrac{dP}{dt}=rP(1−\dfrac{P}{K}).$

Essa linha de fase mostra que quando$P$ é menor que zero ou maior que$K$, a população diminui com o tempo. Quando$P$ está entre$0$ e$K$, a população aumenta com o tempo.

Exemplo$\PageIndex{1}$: Examining the Carrying Capacity of a Deer Population

Vamos considerar a população de veados de cauda branca (Odocoileus virginianus) no estado de Kentucky. O Departamento de Recursos de Peixes e Vida Selvagem de Kentucky (KDFWR) define diretrizes para caça e pesca no estado. Antes da temporada de caça de 2004, estimou-se uma população de 900.000 veados. Johnson observa: “Uma população de veados que tem muito o que comer e não é caçada por humanos ou outros predadores dobrará a cada três anos”. (George Johnson, “The Problem of Exploding Deer Populations Has No Attractive Solutions”, 12 de janeiro de 2001, acessado em 9 de abril de 2015)

Esta é a fotografia de um veado. — Figura$\PageIndex{3}$: (crédito: modificação do trabalho de Rachel Kramer, Flickr)

Essa observação corresponde a uma taxa de aumento$r=\dfrac{\ln (2)}{3}=0.2311,$, então a taxa de crescimento aproximada é de 23,11% ao ano. (Isso pressupõe que a população cresça exponencialmente, o que é razoável — pelo menos no curto prazo — com abundante suprimento de alimentos e sem predadores.) O KDFWR também relata densidades populacionais de veados em 32 condados em Kentucky, cuja média é de aproximadamente 27 cervos por milha quadrada. Suponha que essa seja a densidade de veados para todo o estado (39.732 milhas quadradas). A capacidade de carga$K$ é de 39.732 milhas quadradas vezes 27 cervos por milha quadrada, ou 1.072.764 cervos.

Para esta aplicação, temos$P_0=900,000,K=1,072,764,$ e$r=0.2311.$ substituímos esses valores na Equação\ ref {logisticDiffEq} e formamos o problema do valor inicial.
Resolva o problema do valor inicial da parte a.
De acordo com esse modelo, qual será a população em$3$ anos? Lembre-se de que o tempo de duplicação previsto por Johnson para a população de veados foi de$3$ anos. Como esses valores se comparam?

Suponha que a população consiga chegar a 1.200.000. O que a equação logística prevê que acontecerá com a população nesse cenário?

Solução

a. O problema do valor inicial é

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right),\,\,P(0)=900,000. \nonumber \]

b. A equação logística é uma equação diferencial autônoma, então podemos usar o método de separação de variáveis.

Etapa 1: Definir o lado direito igual a zero dá$P=0$ e$P=1,072,764.$ Isso significa que, se a população começar em zero, ela nunca mudará e, se começar na capacidade de carga, nunca mudará.

Etapa 2: Reescreva a equação diferencial e multiplique os dois lados por:

\[ \begin{align*} \dfrac{dP}{dt} =0.2311P\left(\dfrac{1,072,764−P}{1,072,764} \right) \\[4pt] dP =0.2311P\left(\dfrac{1,072,764−P}{1,072,764}\right)dt \\[4pt] \dfrac{dP}{P(1,072,764−P)} =\dfrac{0.2311}{1,072,764}dt. \end{align*}\]

Etapa 3: Integre os dois lados da equação usando decomposição parcial de frações:

\[ \begin{align*} ∫\dfrac{dP}{P(1,072,764−P)} =∫\dfrac{0.2311}{1,072,764}dt \\[4pt] \dfrac{1}{1,072,764}∫ \left(\dfrac{1}{P}+\dfrac{1}{1,072,764−P}\right)dP =\dfrac{0.2311t}{1,072,764}+C \\[4pt] \dfrac{1}{1,072,764}\left(\ln |P|−\ln |1,072,764−P|\right) =\dfrac{0.2311t}{1,072,764}+C. \end{align*} \nonumber \]

Etapa 4: multiplique os dois lados por 1.072.764 e use a regra do quociente para logaritmos:

\[\ln \left|\dfrac{P}{1,072,764−P}\right|=0.2311t+C_1. \nonumber \]

Aqui, em$C_1=1,072,764C.$ seguida, exponencie os dois lados e elimine o valor absoluto:

\[ \begin{align*} e^{\ln \left|\dfrac{P}{1,072,764−P} \right|} =e^{0.2311t + C_1} \\[4pt] \left|\dfrac{P}{1,072,764 - P}\right| =C_2e^{0.2311t} \\[4pt] \dfrac{P}{1,072,764−P} =C_2e^{0.2311t}. \end{align*}\]

Aqui$C_2=e^{C_1}$, mas depois de eliminar o valor absoluto, ele também pode ser negativo. Agora resolva para:

\[ \begin{align*} P =C_2e^{0.2311t}(1,072,764−P) \\[4pt] P =1,072,764C_2e^{0.2311t}−C_2Pe^{0.2311t} \\[4pt] P + C_2Pe^{0.2311t} = 1,072,764C_2e^{0.2311t} \\[4pt] P(1+C_2e^{0.2311t} =1,072,764C_2e^{0.2311t} \\[4pt] P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.23\nonumber11t}}. \end{align*}\]

Etapa 5: Para determinar o valor de$C_2$, na verdade, é mais fácil voltar algumas etapas para onde$C_2$ foi definido. Em particular, use a equação

\[\dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

A condição inicial é$P(0)=900,000$. $P$Substitua por$900,000$ e$t$ por zero:

\[ \begin{align*} \dfrac{P}{1,072,764−P} =C_2e^{0.2311t} \\[4pt] \dfrac{900,000}{1,072,764−900,000} =C_2e^{0.2311(0)} \\[4pt] \dfrac{900,000}{172,764} =C_2 \\[4pt] C_2 =\dfrac{25,000}{4,799} \\[4pt] ≈5.209. \end{align*}\]

Portanto

\[ \begin{align*} P(t) =\dfrac{1,072,764 \left(\dfrac{25000}{4799}\right)e^{0.2311t}}{1+(250004799)e^{0.2311t}}\\[4pt] =\dfrac{1,072,764(25000)e^{0.2311t}}{4799+25000e^{0.2311t}.} \end{align*}\]

Dividindo o numerador e o denominador por 25.000 dá

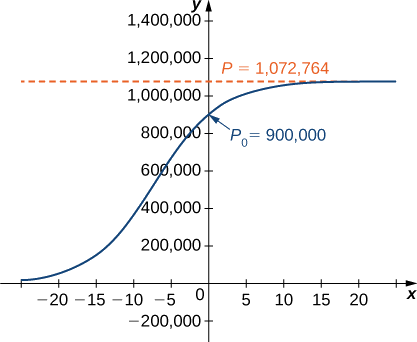
\[P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

A figura é um gráfico dessa equação.

Um gráfico de uma curva logística para a população de veados com uma população inicial P_0 de 900.000. O gráfico começa como uma função ascendente côncava crescente no quadrante dois, muda para uma função crescente côncava descendente, cruza o eixo x em (0, 900.000) e se aproxima assintoticamente de P = 1.072.764 quando x vai para o infinito. — Figura$\PageIndex{4}$: Curva logística para a população de veados com uma população inicial de **900.000** veados.

c. Usando esse modelo, podemos prever a população em 3 anos.

\[P(3)=\dfrac{1,072,764e^{0.2311(3)}}{0.19196+e^{0.2311(3)}}≈978,830\,deer \nonumber \]

Isso é muito menos do dobro da população inicial de$900,000.$ Lembre-se de que o tempo de duplicação é baseado na suposição de que a taxa de crescimento nunca muda, mas o modelo logístico leva em consideração essa possibilidade.

d. Se a população atingisse 1.200.000 cervos, o novo problema do valor inicial seria

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right), \, P(0)=1,200,000. \nonumber \]

A solução geral para a equação diferencial permaneceria a mesma.

\[ P(t)=\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \nonumber \]

Para determinar o valor da constante, retorne à equação

\[ \dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

Substituindo os valores$t=0$ e$P=1,200,000,$ você obtém

\[ \begin{align*} C_2e^{0.2311(0)} =\dfrac{1,200,000}{1,072,764−1,200,000} \\[4pt] C_2 =−\dfrac{100,000}{10,603}≈−9.431.\end{align*}\]

Portanto

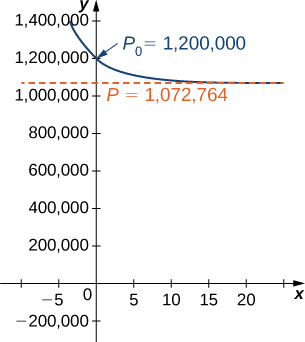
\[ \begin{align*} P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \\[4pt] =\dfrac{1,072,764 \left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}}{1+\left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}} \\[4pt] =−\dfrac{107,276,400,000e^{0.2311t}}{100,000e^{0.2311t}−10,603} \\[4pt] ≈\dfrac{10,117,551e^{0.2311t}}{9.43129e^{0.2311t}−1} \end{align*}\]

Essa equação está representada graficamente na Figura$\PageIndex{5}$.

Um gráfico da curva logística para uma população inicial de 1.200.000 cervos. O gráfico é uma função ascendente côncava decrescente que começa no quadrante dois, cruza o eixo y em (0, 1.200.000) e se aproxima assintoticamente de P = 1.072.764 quando x vai para o infinito. — Figura$\PageIndex{5}$: Curva logística para a população de veados com uma população inicial de **1.200.000** veados.

Resolvendo a equação diferencial logística

A equação diferencial logística é uma equação diferencial autônoma, então podemos usar a separação de variáveis para encontrar a solução geral, como acabamos de fazer em Example$\PageIndex{1}$.

Etapa 1: Definir o lado direito igual a zero leva a$P=0$ e$P=K$ como soluções constantes. A primeira solução indica que, quando não há organismos presentes, a população nunca crescerá. A segunda solução indica que quando a população começa com a capacidade de carga, ela nunca mudará.

Etapa 2: Reescrever a equação diferencial no formulário

\[ \dfrac{dP}{dt}=\dfrac{rP(K−P)}{K}. \nonumber \]

Em seguida, multiplique os dois lados por$dt$ e divida os dois lados por$P(K−P).$ Isso leva a

\[ \dfrac{dP}{P(K−P)}=\dfrac{r}{K}dt. \nonumber \]

Multiplique os dois lados da equação por$K$ e integre:

\[ ∫\dfrac{K}{P(K−P)}dP=∫rdt. \label{eq20a} \]

O lado esquerdo dessa equação pode ser integrado usando decomposição parcial de frações. Deixamos que você verifique se

\[ \dfrac{K}{P(K−P)}=\dfrac{1}{P}+\dfrac{1}{K−P}. \nonumber \]

Em seguida, a Equação\ ref {eq20a} se torna

\[ ∫\dfrac{1}{P}+\dfrac{1}{K−P}dP=∫rdt \nonumber \]

\[ \ln |P|−\ln |K−P|=rt+C \nonumber \]

\[ \ln ∣\dfrac{P}{K−P}∣=rt+C. \nonumber \]

Agora exponencie os dois lados da equação para eliminar o logaritmo natural:

\[ e^{\ln ∣\dfrac{P}{K−P}∣}=e^{rt+C} \nonumber \]

\[ ∣\dfrac{P}{K−P}∣=e^Ce^{rt}. \nonumber \]

Nós definimos$C_1=e^c$ para que a equação se torne

\[ \dfrac{P}{K−P}=C_1e^{rt}. \label{eq30a} \]

Para resolver essa equação$P(t)$, primeiro multiplique os dois lados por$K−P$ e colete os termos contidos$P$ no lado esquerdo da equação:

\[\begin{align*} P =C_1e^{rt}(K−P) \\[4pt] =C_1Ke^{rt}−C_1Pe^{rt} \\[4pt] P+C_1Pe^{rt} =C_1Ke^{rt}.\end{align*}\]

Em seguida, fatore$P$ do lado esquerdo e divida os dois lados pelo outro fator:

\[\begin{align*} P(1+C_1e^{rt}) =C_1Ke^{rt} \\[4pt] P(t) =\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}. \end{align*}\]

A última etapa é determinar o valor de$C_1.$ A maneira mais fácil de fazer isso é substituir$t=0$ e$P_0$ no lugar de$P$ em Equação e resolver por$C_1$:

\[\begin{align*} \dfrac{P}{K−P} = C_1e^{rt} \\[4pt] \dfrac{P_0}{K−P_0} =C_1e^{r(0)} \\[4pt] C_1 = \dfrac{P_0}{K−P_0}. \end{align*}\]

Finalmente, substitua a expressão por$C_1$ na Equação\ ref {eq30a}:

\[ P(t)=\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}=\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \nonumber \]

Agora multiplique o numerador e o denominador do lado direito$(K−P_0)$ e simplifique:

\[\begin{align*} P(t) =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \\[4pt] =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}}⋅\dfrac{K−P_0}{K−P_0} =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}. \end{align*}\]

Declaramos esse resultado como um teorema.

Solução da equação diferencial logística

Considere a equação diferencial logística sujeita a uma população inicial de$P_0$ com capacidade de carga$K$ e taxa de crescimento$r$. A solução para o problema do valor inicial correspondente é dada por

\[P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \nonumber \].

Agora que temos a solução para o problema do valor inicial, podemos escolher valores para$P_0,r$$K$ e estudar a curva da solução. Por exemplo, em Exemplo, usamos os valores$r=0.2311,K=1,072,764,$ e uma população inicial de$900,000$ veados. Isso leva à solução

\[\begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{(1,072,764−900,000)+900,000e^{0.2311t}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{172,764+900,000e^{0.2311t}}.\end{align*}\]

Dividindo a parte superior e inferior por$900,000$ dá

\[ P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

Isso é o mesmo que a solução original. O gráfico dessa solução é mostrado novamente em azul na Figura$\PageIndex{6}$, sobreposto ao gráfico do modelo de crescimento exponencial com população inicial$900,000$ e taxa de crescimento$0.2311$ (aparecendo em verde). A linha tracejada vermelha representa a capacidade de carga e é uma assíntota horizontal para a solução da equação logística.

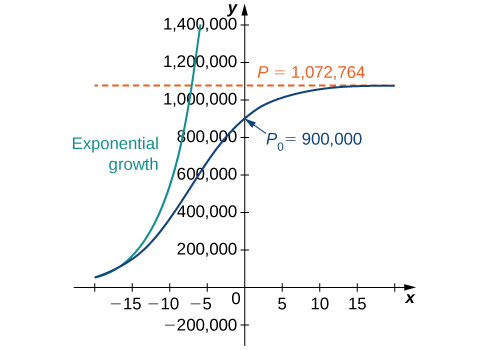
Um gráfico mostrando crescimento exponencial e logístico para a mesma população inicial de 900.000 organismos e taxa de crescimento de 23,11%. Ambos começam no quadrante dois, próximo ao eixo x, como curvas ascendentes côncavas crescentes. A curva de crescimento exponencial continua crescendo, passando P = 1.072.764 enquanto ainda está no quadrante dois. A curva de crescimento logístico muda a concavidade, cruza o eixo x em P_0 = 900.000 e se aproxima assintoticamente de P = 1.072.764. — Figura$\PageIndex{6}$: Uma comparação do crescimento exponencial versus crescimento logístico para a mesma população inicial de$900,000$ organismos e taxa de crescimento de$23.11%.$

Partindo do pressuposto de que a população cresce de acordo com a equação diferencial logística, este gráfico prevê que, aproximadamente$20$ anos antes$(1984)$, o crescimento da população foi muito próximo do exponencial. A taxa de crescimento líquida naquela época teria sido de cerca de um$23.1%$ ano. Conforme o tempo passa, os dois gráficos se separam. Isso acontece porque a população aumenta e a equação diferencial logística afirma que a taxa de crescimento diminui à medida que a população aumenta. Na época em que a população foi medida$(2004)$, estava próxima da capacidade de carga e a população estava começando a se estabilizar.

A solução para a equação diferencial logística tem um ponto de inflexão. Para encontrar esse ponto, defina a segunda derivada igual a zero:

\[ \begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \\[4pt] P′(t) =\dfrac{rP_0K(K−P0)e^{rt}}{((K−P_0)+P_0e^{rt})^2} \\[4pt] P''(t) =\dfrac{r^2P_0K(K−P_0)^2e^{rt}−r^2P_0^2K(K−P_0)e^{2rt}}{((K−P_0)+P_0e^{rt})^3} \\[4pt] =\dfrac{r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})}{((K−P_0)+P_0e^{rt})^3}. \end{align*}\]

Definindo o numerador igual a zero,

\[ r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})=0. \nonumber \]

Desde que$P_0≠K$ a quantidade total antes e incluída$e^{rt}$ seja diferente de zero, podemos dividi-la:

\[ (K−P_0)−P_0e^{rt}=0. \nonumber \]

Resolvendo para$t$,

\[ P_0e^{rt}=K−P_0 \nonumber \]

\[ e^{rt}=\dfrac{K−P_0}{P_0} \nonumber \]

\[ \ln e^{rt}=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ rt=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ t=\dfrac{1}{r}\ln \dfrac{K−P_0}{P_0}. \nonumber \]

Observe que se$P_0>K$, então essa quantidade é indefinida e o gráfico não tem um ponto de inflexão. No gráfico logístico, o ponto de inflexão pode ser visto como o ponto em que o gráfico muda de côncavo para cima para côncavo para baixo. É aqui que o “nivelamento” começa a ocorrer, porque a taxa líquida de crescimento se torna mais lenta à medida que a população começa a se aproximar da capacidade de carga.

Exercício$\PageIndex{1}$

Observa-se que uma população de coelhos em um prado às vezes são$200$ coelhos$t=0$. Depois de um mês, observa-se que a população de coelhos aumentou em$4%$. Usando uma população inicial de$200$ e uma taxa de crescimento de$0.04$, com uma capacidade de carga de$750$ coelhos,

Escreva a equação diferencial logística e a condição inicial para esse modelo.
Desenhe um campo de inclinação para essa equação diferencial logística e esboce a solução correspondente a uma população inicial de$200$ coelhos.
Resolva o problema do valor inicial do$P(t)$.
Use a solução para prever a população após$1$ um ano.

Dica: Primeiro determine os valores de$r,K,$$P_0$ e. Em seguida, crie o problema do valor inicial, desenhe o campo de direção e resolva o problema.

Resposta

uma.$\dfrac{dP}{dt}=0.04(1−\dfrac{P}{750}),P(0)=200$

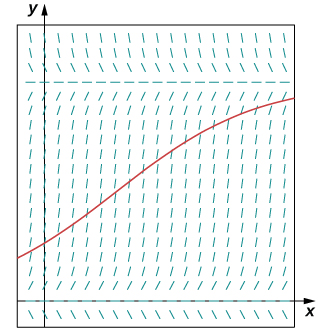
$Um campo de direção com linhas horizontais no eixo x e y = 15. As outras linhas são verticais, exceto aquelas que se curvam no eixo x e y = 15. É desenhada uma solução que cruza o eixo y em cerca de (0, 4) e se aproxima assintoticamente de y = 15.$

c.$P(t)=\dfrac{3000e^{.04t}}{11+4e^{.04t}}$

d. Depois de$12$ meses, a população será de$P(12)≈278$ coelhos.

Projeto do Aluno: Equação Logística com uma População Limite

Uma melhoria no modelo logístico inclui uma população limite. A população limite é definida como a população mínima necessária para a sobrevivência da espécie. Usamos a variável$T$ para representar a população limite. Uma equação diferencial que incorpora a população limite$T$ e a capacidade de carga$K$ é

\[ \dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right) \nonumber \]

onde$r$ representa a taxa de crescimento, como antes.

A população limite é útil para biólogos e pode ser utilizada para determinar se uma determinada espécie deve ser colocada na lista de ameaçados de extinção. Um grupo de pesquisadores australianos afirma ter determinado o limite populacional para qualquer espécie sobreviver:$5000$ adultos. (Catherine Clabby, “A Magic Number”, American Scientist 98 (1): 24, doi:10.1511/2010.82.24. acessado em 9 de abril de 2015, www.americanscientist.org/iss... a-magic-number). Portanto, usamos$T=5000$ como população limite neste projeto. Suponha que a capacidade de carga ambiental em Montana para alces seja$25,000$. Configure a equação usando a capacidade de carga$25,000$ e a população limite de$5000$. Suponha uma taxa de crescimento líquido anual de 18%.
Desenhe o campo de direção para a equação diferencial a partir da etapa$1$, junto com várias soluções para diferentes populações iniciais. Quais são as soluções constantes da equação diferencial? A que essas soluções correspondem no modelo populacional original (ou seja, em um contexto biológico)?
Qual é a população limite para cada população inicial que você escolheu por etapas$2$? (Dica: use o campo de inclinação para ver o que acontece com várias populações iniciais, ou seja, procure as assíntotas horizontais de suas soluções.)
Essa equação pode ser resolvida usando o método de separação de variáveis. No entanto, é muito difícil obter a solução como uma função explícita do$t$. Usando uma população inicial de$18,000$ alces, resolva o problema do valor inicial e expresse a solução como uma função implícita de t, ou resolva o problema geral do valor inicial, encontrando uma solução em termos de$r,K,T,$$P_0$ e.

Conceitos chave

Ao estudar as funções populacionais, diferentes suposições — como crescimento exponencial, crescimento logístico ou limiar populacional — levam a diferentes taxas de crescimento.
A equação diferencial logística incorpora o conceito de capacidade de carga. Esse valor é um valor limitante na população de qualquer ambiente.
A equação diferencial logística pode ser resolvida para qualquer taxa de crescimento positiva, população inicial e capacidade de carga.

Equações chave

Equação diferencial logística e problema de valor inicial

$\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right),\quad P(0)=P_0$

Solução para o problema da equação diferencial logística/valor inicial

$P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}$

Modelo de população limite

$\dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right)$

Glossário

capacidade de carga: a população máxima de um organismo que o meio ambiente pode sustentar indefinidamente

taxa de crescimento: a constante$r>0$ na função de crescimento exponencial$P(t)=P_0e^{rt}$

população inicial: a população no momento$t=0$

equação diferencial logística: uma equação diferencial que incorpora a capacidade de carga$K$ e a taxa de crescimento rr em um modelo populacional

linha de fase: uma representação visual do comportamento de soluções para uma equação diferencial autônoma sujeita a várias condições iniciais

população limite: a população mínima necessária para que uma espécie sobreviva

Definição: Capacidade de transporte

Definição: Equação diferencial logística

Exemplo\(\PageIndex{1}\): Examining the Carrying Capacity of a Deer Population

Solução da equação diferencial logística

Exercício\(\PageIndex{1}\)

Projeto do Aluno: Equação Logística com uma População Limite