Skip to main content
Global

8.3E: Exercícios para a Seção 8.3

  1. Last updated
  2. Save as PDF
  • Page ID
    188078

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nos exercícios 1 a 4, resolva os seguintes problemas de valor inicial com a condição inicial\( y_0=0\) e represente graficamente a solução.

    1)\( \dfrac{dy}{dt}=y+1\)

    Resposta
    \( y=e^t−1\)

    2)\( \dfrac{dy}{dt}=y−1\)

    3)\( \dfrac{dy}{dt}=-y+1\)

    Resposta
    \( y=1−e^{−t}\)

    4)\( \dfrac{dy}{dt}=−y−1\)

    Nos exercícios 5 a 14, encontre a solução geral para a equação diferencial.

    5)\( x^2y'=(x+1)y\)

    Resposta
    \( y=Cxe^{−1/x}\)

    6)\( y'=\tan(y)x\)

    7)\( y'=2xy^2\)

    Resposta
    \( y=\dfrac{1}{C−x^2}\)

    8)\( \dfrac{dy}{dt}=y\cos(3t+2)\)

    9)\( 2x\dfrac{dy}{dx}=y^2\)

    Resposta
    \( y=−\dfrac{2}{C+\ln|x|}\)

    10)\( y'=e^yx^2\)

    11)\( (1+x)y'=(x+2)(y−1)\)

    Resposta
    \( y=Ce^x(x+1)+1\)

    12)\( \dfrac{dx}{dt}=3t^2(x^2+4)\)

    13)\( t\dfrac{dy}{dt}=\sqrt{1−y^2}\)

    Resposta
    \( y=\sin(\ln|t|+C)\)

    14)\( y'=e^xe^y\)

    Nos exercícios 15 a 24, encontre a solução para o problema do valor inicial.

    15)\( y'=e^{y−x}, \quad y(0)=0\)

    Resposta
    \( y=−\ln(e^{−x})\)o que simplifica para\(y = x\)

    16)\( y'=y^2(x+1), \quad y(0)=2\)

    17)\( \dfrac{dy}{dx}=y^3xe^{x^2}, \quad y(0)=1\)

    Resposta
    \( y=\dfrac{1}{\sqrt{2−e^{x^2}}}\)

    18)\( \dfrac{dy}{dt}=y^2e^x\sin(3x), \quad y(0)=1\)

    19)\( y'=\dfrac{x}{\text{sech}^2y}, \quad y(0)=0\)

    Resposta
    \( y=\tanh^{−1}\left(\dfrac{x^2}{2}\right)\)

    20)\( y'=2xy(1+2y), \quad y(0)=−1\)

    21)\( \dfrac{dx}{dt}=\ln(t)\sqrt{1−x^2}, \quad x(1)=0\)

    Resposta
    \( x=\sin(1 - t + t\ln t)\)

    22)\( y'=3x^2(y^2+4),\quad y(0)=0\)

    23)\( y'=e^y5^x, \quad y(0)=\ln(\ln(5))\)

    Resposta
    \( y=\ln(\ln(5))−\ln(2−5^x)\)

    24)\( y'=−2x\tan(y), \quad y(0)=\dfrac{π}{2}\)

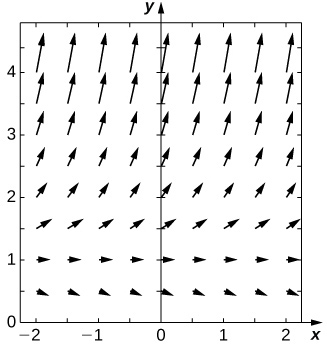
    Para problemas de 25 a 29, use um programa de software ou sua calculadora para gerar os campos direcionais. Resolva explicitamente e desenhe curvas de solução para várias condições iniciais. Existem algumas condições iniciais críticas que mudam o comportamento da solução?

    25) [T]\( y'=1−2y\)

    Resposta

    \( y=Ce^{−2}x+\dfrac{1}{2}\)

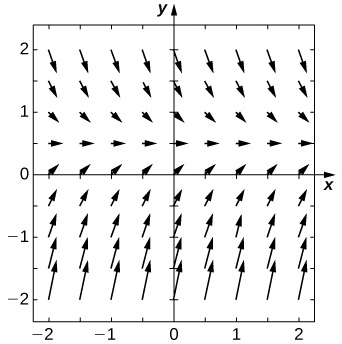
    26) [T]\( y'=y^2x^3\)

    27) [T]\( y'=y^3e^x\)

    Resposta

    \( y=\dfrac{1}{\sqrt{2}\sqrt{C−e^x}}\)

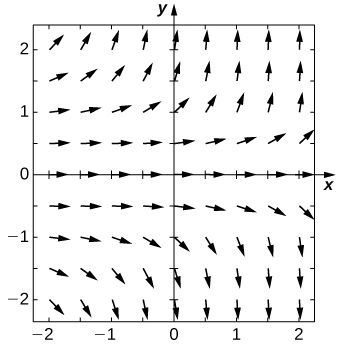
    28) [T]\( y'=e^y\)

    29) [T]\( y'=y\ln(x)\)

    Resposta

    \( y=Ce^{−x}x^x\)

    30) A maioria dos medicamentos na corrente sanguínea se decompõe de acordo com a equação\( y'=cy\), onde\( y\) está a concentração da droga na corrente sanguínea. Se a meia-vida de um medicamento for de\( 2\) horas, qual fração da dose inicial permanece após\( 6\) horas?

    31) Um medicamento é administrado por via intravenosa a um paciente na taxa\( r\) mg/h e é eliminado do corpo em uma taxa proporcional à quantidade de medicamento ainda presente no corpo.\( d\) Configure e resolva a equação diferencial, assumindo que não há nenhum medicamento inicialmente presente no corpo.

    Resposta
    \( y=\frac{r}{d}(1−e^{−dt})\)

    32) [T] Com que frequência um medicamento deve ser tomado se sua dose for\( 3\) mg, for eliminado a uma taxa de\( c=0.1\) mg/h e se for necessário que\( 1\) mg esteja sempre na corrente sanguínea?

    33) Um tanque contém\( 1\) quilograma de sal dissolvido em\( 100\) litros de água. Uma solução salina de\( 0.1\) kg de sal/L é bombeada para o tanque a uma taxa de\( 2\) L/min e drenada na mesma taxa. Resolva a concentração de sal de cada vez\( t\). Suponha que o tanque esteja bem misturado.

    Resposta
    \( y(t)=10−9e^{−t/50}\)

    34) Um tanque contendo\( 10\) quilogramas de sal dissolvido em\( 1000\) litros de água tem duas soluções de sal bombeadas. A primeira solução de\( 0.2\) kg de sal/L é bombeada a uma taxa de\( 20\) L/min e a segunda solução de\( 0.05\) kg de sal/L é bombeada a uma taxa de\( 5\) L/min. O tanque drena a\( 25\) L/min. Suponha que o tanque esteja bem misturado. Resolva a concentração de sal de cada vez\( t\).

    35) [T] Para o problema anterior, descubra a quantidade de sal no tanque\( 1\) uma hora após o início do processo.

    Resposta
    \( 134.3\)quilogramas

    36) A lei de Torricelli estabelece que, para um tanque de água com um orifício no fundo que tem uma seção transversal de\( A\) e com uma altura de água\( h\) acima do fundo do tanque, a taxa de variação do volume de água que flui do tanque é proporcional à raiz quadrada da altura da água, de acordo com para\( \dfrac{dV}{dt}=−A\sqrt{2gh}\), onde\( g\) está a aceleração devido à gravidade. Observe isso\( \dfrac{dV}{dt}=A\dfrac{dh}{dt}\). Resolva o problema do valor inicial resultante para a altura da água, assumindo um tanque com um orifício de raio\( 2\) ft. A altura inicial da água é de\( 100\) pés.

    37) Para o problema anterior, determine quanto tempo o tanque leva para drenar.

    Resposta
    \( 720\)segundos

    Para problemas 38 a 44, use a lei de resfriamento de Newton.

    38) A base líquida de um sorvete tem uma temperatura inicial de\( 200°F\) antes de ser colocada em um freezer com temperatura constante de\( 0°F\). Depois de\( 1\) uma hora, a temperatura da base de sorvete diminuiu para\( 140°F\). Formule e resolva o problema do valor inicial para determinar a temperatura do sorvete.

    39) [T] A base líquida de um sorvete tem uma temperatura inicial de\( 210°F\) antes de ser colocada em um freezer com uma temperatura constante de\( 20°F\). Depois de\( 2\) horas, a temperatura da base de sorvete diminuiu para\( 170°F\). A que horas o sorvete estará pronto para comer? (Suponha que\( 30°F\) seja a temperatura ideal para comer.)

    Resposta
    \( 24\)horas\( 55\) minutos

    40) [T] Você está organizando um evento social de sorvete. A temperatura externa está\( 80°F\) e o sorvete está em\( 10°F\). Depois de\( 10\) minutos, a temperatura do sorvete aumentou\( 10°F\). Quanto tempo você pode esperar até que o sorvete derreta\( 40°F\)?

    41) Você toma uma xícara de café em temperatura\( 70°C\) e a temperatura ambiente na sala é\( 20°C\). Assumindo uma taxa\( k\) de resfriamento de\( 0.125,\) escrever e resolver a equação diferencial para descrever a temperatura do café em relação ao tempo.

    Resposta
    \( T(t)=20+50e^{−0.125t}\)

    42) [T] Você toma uma xícara de café em temperatura\( 70°C\) que você coloca lá fora, onde a temperatura ambiente é\( 0°C.\) Depois de\( 5\) minutos, quanto mais frio está o café?

    43) Você toma uma xícara de café em temperatura\( 70°C\) e imediatamente despeja\( 1\) parte do leite em\( 5\) partes de café. O leite está inicialmente na temperatura\( 1°C.\) Escreva e resolva a equação diferencial que governa a temperatura desse café.

    Resposta
    \( T(t)=20+38.5e^{−0.125t}\)

    44) Você toma uma xícara de café em temperatura\( 70°C,\) que deixa esfriar\( 10\) minutos antes de despejar a mesma quantidade de leite que no problema anterior.\( 1°C\) Como a temperatura se compara à xícara anterior após\( 10\) alguns minutos?

    45) Resolva o problema genérico\( y'=ay+b\) com a condição inicial\( y(0)=c.\)

    Resposta
    \( y=(c+ba)e^{ax}−\frac{b}{a}\)

    46) Prove a equação básica de juros compostos contínuos. Supondo um depósito inicial\( P_0\) e uma taxa de juros de\( r\), configure e resolva uma equação para juros continuamente compostos.

    47) Suponha uma quantidade inicial de nutrientes de\( I\) quilogramas em um tanque com\( L\) litros. Suponha que uma concentração de\( c\) kg/L seja bombeada a uma taxa de\( r\) L/min. O tanque está bem misturado e é drenado a uma taxa de\( r\) L/min. Encontre a equação que descreve a quantidade de nutrientes no tanque.

    Resposta
    \( y(t)=cL+(I−cL)e^{−rt/L}\)

    48) As folhas se acumulam no solo da floresta a uma taxa de\( 2\) g/cm 2/ano e também se decompõem a uma taxa de\( 90%\) por ano. Escreva uma equação diferencial governando o número de gramas de serapilheira por centímetro quadrado do solo da floresta, assumindo que no momento não\( 0\) há serapilheira no solo. Esse valor se aproxima de um valor estável? Qual é esse valor?

    49) As folhas se acumulam no solo da floresta a uma taxa de\( 4\) g/cm 2 /ano. Essas folhas se decompõem a uma taxa de\( 10%\) por ano. Escreva uma equação diferencial governando o número de gramas de serapilheira por centímetro quadrado do solo da floresta. Esse valor se aproxima de um valor estável? Qual é esse valor?

    Resposta
    Equação diferencial:\(\dfrac{dy}{dt} = 4 - 0.1y\)
    Solução, o modelo para esta situação:\( y=40(1−e^{−0.1t})\),
    Quantidade se aproxima de um valor estável de 40 g/cm 2