8.3: Equações separáveis

Last updated
Save as PDF

Page ID: 188066

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Use a separação de variáveis para resolver uma equação diferencial.
Resolva aplicativos usando a separação de variáveis.

Agora examinamos uma técnica de solução para encontrar soluções exatas para uma classe de equações diferenciais conhecidas como equações diferenciais separáveis. Essas equações são comuns em uma ampla variedade de disciplinas, incluindo física, química e engenharia. Ilustramos algumas aplicações no final da seção.

Separação de variáveis

Começamos com uma definição e alguns exemplos.

Definição: Equações diferenciais separáveis

Uma equação diferencial separável é qualquer equação que possa ser escrita na forma

\[y'=f(x)g(y). \label{sep} \]

O termo 'separável' se refere ao fato de que o lado direito da Equação\ ref {sep} pode ser separado em uma função de$x$ vezes uma função de$y$. Exemplos de equações diferenciais separáveis incluem

\[ \begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align} \]

A equação\ ref {eq2} é separável com$f(x)=6x^2+4x$ e$g(y)=1$, a Equação\ ref {eq3} é separável com$f(x)=1$$g(y)=\sec y+\tan y,$ e e o lado direito da Equação\ ref {eq4} pode ser fatorado como$(x+3)(y−2)$, então também é separável. A equação\ ref {eq3} também é chamada de equação diferencial autônoma porque o lado direito da equação é uma função da$y$ solidão. Se uma equação diferencial for separável, é possível resolver a equação usando o método de separação de variáveis.

Estratégia de resolução de problemas: separação de variáveis

Verifique se há valores$y$ que$g(y)=0.$ fazem com que correspondam a soluções constantes.
Reescreva a equação diferencial no formulário\[ \dfrac{dy}{g(y)}=f(x)dx. \nonumber \]
Integre os dois lados da equação.
Resolva a equação resultante,$y$ se possível.
Se existir uma condição inicial, substitua os valores apropriados por$x$ e$y$ na equação e resolva a constante.

Observe que a Etapa 4 afirma “Resolva a equação resultante,$y$ se possível”. Nem sempre é possível obter$y$ como função explícita de$x$. Muitas vezes, temos que ficar satisfeitos em encontrar y como uma função implícita de$x$.

Exemplo$\PageIndex{1}$: Using Separation of Variables

Encontre uma solução geral para a equação diferencial$y'=(x^2−4)(3y+2)$ usando o método de separação de variáveis.

Solução

Siga o método de cinco etapas de separação de variáveis.

1. Neste exemplo,$f(x)=x^2−4$$g(y)=3y+2$ e. A configuração$g(y)=0$ fornece$y=−\dfrac{2}{3}$ uma solução constante.

2. Reescreva a equação diferencial no formulário

\[ \dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber \]

3. Integre os dois lados da equação:

\[ ∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber \]

Deixe$u=3y+2$. Então$du=3\dfrac{dy}{dx}\,dx$, então a equação se torna

\[ \dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber \]

\[ \dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber \]

4. Para resolver essa equação$y$, primeiro multiplique os dois lados da equação por$3$.

\[ \ln|3y+2|=x^3−12x+3C\nonumber \]

Agora usamos alguma lógica para lidar com a constante$C$. Uma vez que$C$ representa uma constante arbitrária,$3C$ também representa uma constante arbitrária. Se chamarmos a segunda constante arbitrária$C_1,$ onde$C_1 = 3C,$ a equação se torna

\[ \ln|3y+2|=x^3−12x+C_1.\nonumber \]

Agora exponencie os dois lados da equação (ou seja, faça de cada lado da equação o expoente da base$e$).

\[ \begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}\]

Defina novamente uma nova constante$C_2= e^{C_1}$ (observe que$C_2 > 0$):

\[ |3y+2|=C_2e^{x^3−12x}.\nonumber \]

Por causa do valor absoluto no lado esquerdo da equação, isso corresponde a duas equações separadas:

\[3y+2=C_2e^{x^3−12x}\nonumber \]

\[3y+2=−C_2e^{x^3−12x}.\nonumber \]

A solução para qualquer equação pode ser escrita na forma

\[y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber \]

Como$C_2>0$ não importa se usamos mais ou menos, a constante pode realmente ter qualquer um dos sinais. Além disso, o subscrito na constante$C$ é totalmente arbitrário e pode ser descartado. Portanto, a solução pode ser escrita como

\[ y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber \]

Observe que, ao escrever uma única solução geral dessa maneira, também estamos permitindo$C$ a igualdade$0$. Isso nos dá a solução singular,$y = -\dfrac{2}{3}$, para a equação diferencial dada. Verifique se isso é realmente uma solução dessa equação diferencial!

5. Nenhuma condição inicial é imposta, então terminamos.

Exercício$\PageIndex{1}$

Use o método de separação de variáveis para encontrar uma solução geral para a equação diferencial

\[ y'=2xy+3y−4x−6. \nonumber \]

Dica: Primeiro fatore o lado direito da equação por meio do agrupamento e, em seguida, use a estratégia de cinco etapas de separação de variáveis.
Responda: \[ y=2+Ce^{x^2+3x} \nonumber \]

Exemplo$\PageIndex{2}$: Solving an Initial-Value Problem

Usando o método de separação de variáveis, resolva o problema do valor inicial

\[ y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber \]

Solução

Siga o método de cinco etapas de separação de variáveis.

1. Neste exemplo,$f(x)=2x+3$$g(y)=y^2−4$ e. A configuração$g(y)=0$ fornece$y=±2$ soluções constantes.

2. Divida os dois lados da equação por$y^2−4$ e multiplique por$dx$. Isso dá a equação

\[\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber \]

3. Em seguida, integre os dois lados:

\[∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2} \]

Para avaliar o lado esquerdo, use o método de decomposição parcial de frações. Isso leva à identidade

\[\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber \]

Então a Equação\ ref {Ex2.2} se torna

\[\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber \]

\[\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber \]

Multiplicando os dois lados dessa equação$4$ e$4C$ substituindo-os por,$C_1$ dá

\[\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber \]

\[\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber \]

4. É possível resolver essa equação para$y.$ primeiro exponenciar os dois lados da equação e definir$C_2=e^{C_1}$:

\[\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber \]

Em seguida, podemos remover o valor absoluto e deixar uma nova constante$C_3$ ser positiva, negativa ou zero, ou seja,$C_3 =\pm C_2$ ou$C_3 = 0.$

Em seguida, multiplique os dois lados por$y+2$.

\[y−2=C_3(y+2)e^{4x^2+12x}\nonumber \]

\[y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber \]

Agora colete todos os termos envolvidos$y$ em um lado da equação e resolva por$y$:

\[y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber \]

\[y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber \]

\[y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber \]

5. Para determinar o valor de$C_3$, substitua$x=0$ e$y=−1$ na solução geral. Como alternativa, podemos colocar os mesmos valores em uma equação anterior, ou seja, a equação$\dfrac{y−2}{y+2}=C_3e^{4x^2+12}$. Isso é muito mais fácil de resolver para$C_3$:

\[\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber \]

\[\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber \]

\[C_3=−3.\nonumber \]

Portanto, a solução para o problema do valor inicial é

\[y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber \]

Um gráfico dessa solução aparece na Figura$\PageIndex{1}$.

$Um gráfico da solução sobre [-5, 3] para x e [-3, 2] para y. Ele começa como uma linha horizontal em y = -2 de x = -5 até pouco antes de -3, quase imediatamente sobe para y = 2 logo após x = -3 até pouco antes de x = 0 e quase imediatamente volta para y = -2 logo após x = 0 até x = 3.$

Figura$\PageIndex{1}$: Gráfico da solução para o problema do valor inicial$y'=(2x+3)(y^2−4),y(0)=−1$.

Exercício$\PageIndex{2}$

Encontre a solução para o problema do valor inicial

\[ 6y'=(2x+1)(y^2−2y−8) \nonumber \]

com$y(0)=−3$ o uso do método de separação de variáveis.

Dica: Siga as etapas de separação de variáveis para resolver o problema do valor inicial.
Responda: \[ y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber \]

Aplicações da separação de variáveis

Muitos problemas interessantes podem ser descritos por equações separáveis. Ilustramos dois tipos de problemas: concentrações da solução e lei de resfriamento de Newton.

Concentrações da

Considere um tanque sendo preenchido com uma solução salina. Gostaríamos de determinar a quantidade de sal presente no tanque em função do tempo. Podemos aplicar o processo de separação de variáveis para resolver esse problema e problemas similares envolvendo concentrações de soluções.

Exemplo$\PageIndex{3}$: Determining Salt Concentration over Time

Um tanque contendo$100$ L de uma solução de salmoura inicialmente tem$4$ kg de sal dissolvido na solução. De vez em quando$t=0$, outra solução de salmoura flui para o tanque a uma taxa de$2$ L/min. Esta solução de salmoura contém uma concentração de$0.5$ kg/L de sal. Ao mesmo tempo, uma torneira é aberta na parte inferior do tanque, permitindo que a solução combinada flua a uma taxa de$2$ L/min, para que o nível de líquido no tanque permaneça constante (Figura$\PageIndex{2}$). Encontre a quantidade de sal no tanque em função do tempo (medida em minutos) e encontre a quantidade limite de sal no tanque, supondo que a solução no tanque esteja bem misturada o tempo todo.

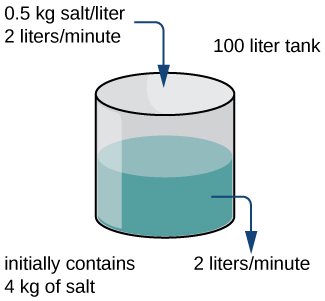
Um diagrama de um cilindro cheio de água com entrada e saída. É um tanque de 100 litros que inicialmente contém 4 kg de sal. A entrada é de 0,5 kg de sal/litro e 2 litros/minuto. A saída é de 2 litros/minuto. — Figura$\PageIndex{2}$: Um tanque de salmoura com uma quantidade inicial de solução salina aceita um fluxo de entrada e fornece um fluxo de saída. Como a quantidade de sal muda com o tempo?

Solução

Primeiro, definimos uma função$u(t)$ que representa a quantidade de sal em quilogramas no tanque em função do tempo. Em seguida,$\dfrac{du}{dt}$ representa a taxa na qual a quantidade de sal no tanque muda em função do tempo. Além disso,$u(0)$ representa a quantidade de sal no tanque por vez$t=0$, que é de$4$ quilogramas.

A configuração geral para a equação diferencial que resolveremos é da forma

\[\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber \]

A TAXA DE ENTRADA representa a taxa na qual o sal entra no tanque, e a TAXA DE FLUXO DE SAÍDA representa a taxa na qual o sal sai do tanque. Como a solução entra no tanque a uma taxa de$2$ L/min e cada litro de solução contém$0.5$ quilograma de sal, a cada minuto,$2(0.5)=1$ quilograma de sal entra no tanque. Portanto, TAXA DE ENTRADA =$1$.

Para calcular a taxa na qual o sal sai do tanque, precisamos da concentração de sal no tanque a qualquer momento. Como a quantidade real de sal varia com o tempo, a concentração de sal também varia. No entanto, o volume da solução permanece fixo em 100 litros. O número de quilos de sal no tanque por vez$t$ é igual$u(t)$ a. Assim, a concentração de sal é$\dfrac{u(t)}{100}$ kg/L e a solução sai do tanque a uma taxa de$2$ L/min. Portanto, o sal sai do tanque a uma taxa de$\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}$ kg/min e a TAXA DE SAÍDA é igual$\dfrac{u(t)}{50}$ a. Portanto, a equação diferencial se torna$\dfrac{du}{dt}=1−\dfrac{u}{50}$, e a condição inicial é$u(0)=4.$ O problema do valor inicial a ser resolvido é

\[\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber \]

A equação diferencial é uma equação separável, então podemos aplicar a estratégia de cinco etapas para solução.

Etapa 1. A configuração$1−\dfrac{u}{50}=0$ fornece$u=50$ uma solução constante. Como a quantidade inicial de sal no tanque é de$4$ quilogramas, essa solução não se aplica.

Etapa 2. Reescreva a equação como

\[\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber \]

Em seguida, multiplique os dois lados por$dt$ e divida os dois lados por$50−u:$

\[\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber \]

Etapa 3. Integre os dois lados:

\[\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}\]

Etapa 4. Resolva para$u(t)$:

\[\ln|50−u|=−\dfrac{t}{50}−C\nonumber \]

\[e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber \]

\[|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber \]

Elimine o valor absoluto permitindo que a constante seja positiva, negativa ou zero, ou seja,$C_1 = \pm e^{-C}$ ou$C_1 = 0$:

\[50−u=C_1e^{−t/50}.\nonumber \]

Finalmente, resolva$u(t)$:

\[u(t)=50−C_1e^{−t/50}.\nonumber \]

Etapa 5. Resolva para$C_1$:

\[\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}\]

A solução para o problema do valor inicial é encontrar$u(t)=50−46e^{−t/50}.$ a quantidade limite de sal no tanque, considere o limite quando$t$ se aproxima do infinito:

\[\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}\]

Observe que essa foi a solução constante para a equação diferencial. Se a quantidade inicial de sal no tanque for de$50$ quilogramas, ela permanecerá constante. Se começar com menos de um$50$ quilograma, ele se aproxima dos$50$ quilos com o tempo.

Exercício$\PageIndex{3}$

Um tanque contém$3$ quilos de sal dissolvidos em$75$ litros de água. Uma solução salina de$0.4$ kg de sal/L é bombeada para o tanque a uma taxa de$6$ L/min e drenada na mesma taxa. Resolva a concentração de sal de cada vez$t$. Suponha que o tanque esteja bem misturado o tempo todo.

Dica

Siga as etapas em Exemplo$\PageIndex{3}$ e determine uma expressão para INFLOW e OUTFLOW. Formule um problema de valor inicial e, em seguida, resolva-o.

Problema de valor inicial:

\[ \dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber \]

Responda

\[u(t)=30−27e^{−t/50} \nonumber \]

Lei do Resfriamento de Newton

A lei de resfriamento de Newton afirma que a taxa de variação da temperatura de um objeto é proporcional à diferença entre sua própria temperatura e a temperatura ambiente (ou seja, a temperatura do ambiente). Se deixarmos$T(t)$ representar a temperatura de um objeto em função do tempo, então$\dfrac{dT}{dt}$ representamos a taxa na qual essa temperatura muda. A temperatura do ambiente do objeto pode ser representada por$T_s$. Então, a lei de resfriamento de Newton pode ser escrita na forma

\[ \dfrac{dT}{dt}=k(T(t)−T_s) \nonumber \]

ou simplesmente

\[ \dfrac{dT}{dt}=k(T−T_s). \nonumber \]

A temperatura do objeto no início de qualquer experimento é o valor inicial para o problema do valor inicial. Chamamos isso de temperatura$T_0$. Portanto, o problema do valor inicial que precisa ser resolvido assume a forma

\[ \dfrac{dT}{dt}=k(T−T_s) \label{newton} \]

com$T(0)=T_0$, onde$k$ está uma constante que precisa ser dada ou determinada no contexto do problema. Usamos essas equações em Example$\PageIndex{4}$.

Exemplo$\PageIndex{4}$: Waiting for a Pizza to Cool

Uma pizza é retirada do forno após assar bem, e a temperatura do forno é$350°F.$ A temperatura da cozinha é$75°F$, e depois de$5$ minutos a temperatura da pizza é$340°F$. Gostaríamos de esperar até que a temperatura da pizza atinja$300°F$ antes de cortá-la e servi-la (Figura$\PageIndex{3}$). Quanto tempo mais teremos que esperar?

Um diagrama de uma torta de pizza. A temperatura ambiente é de 75 graus e a temperatura da pizza é de 350 graus. — Figura$\PageIndex{3}$: Da lei de resfriamento de Newton, se a pizza esfriar$10°F$ em$5$ minutos, quanto tempo até esfriar$300°F$?

Solução

A temperatura ambiente (temperatura ambiente) é$75°F$, portanto$T_s=75$. A temperatura da pizza quando ela sai do forno é$350°F$, que é a temperatura inicial (ou seja, valor inicial), então$T_0=350$. Portanto, a Equação\ ref {newton} se torna

\[\dfrac{dT}{dt}=k(T−75) \nonumber \]

com$T(0)=350.$

Para resolver a equação diferencial, usamos a técnica de cinco etapas para resolver equações separáveis.

1. Definir o lado direito igual a zero fornece$T=75$ uma solução constante. Como a pizza começa$350°F,$ assim, essa não é a solução que buscamos.

2. Reescreva a equação diferencial multiplicando os dois lados por$dt$ e dividindo os dois lados por$T−75$:

\[\dfrac{dT}{T−75}=k\,dt. \nonumber \]

3. Integre os dois lados:

\[\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber \]

4. Resolva para$T$ exponenciando primeiro os dois lados:

\[\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber \]

5. Resolva$C$ por usando a condição inicial$T(0)=350:$

\[\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber \]

Portanto, a solução para o problema do valor inicial é

\[T(t)=75+275e^{kt}.\nonumber \]

Para determinar o valor de$k$, precisamos usar o fato de que após$5$ alguns minutos a temperatura da pizza é$340°F$. Portanto,$T(5)=340.$ substituindo essas informações pela solução para o problema do valor inicial, temos

\[T(t)=75+275e^{kt}\nonumber \]

\[T(5)=340=75+275e^{5k}\nonumber \]

\[265=275e^{5k}\nonumber \]

\[e^{5k}=\dfrac{53}{55}\nonumber \]

\[\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber \]

\[5k=\ln(\dfrac{53}{55})\nonumber \]

\[k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber \]

Então agora temos$T(t)=75+275e^{−0.007048t}.$ Quando é a temperatura$300°F$? Resolvendo para$t,$ nós encontramos

\[T(t)=75+275e^{−0.007048t}\nonumber \]

\[300=75+275e^{−0.007048t}\nonumber \]

\[225=275e^{−0.007048t}\nonumber \]

\[e^{−0.007048t}=\dfrac{9}{11}\nonumber \]

\[\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber \]

\[−0.007048t=\ln\dfrac{9}{11}\nonumber \]

\[t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber \]

Portanto, precisamos esperar mais$23.5$ alguns minutos (após a temperatura da pizza atingir$340°F$). Isso deve ser tempo suficiente para concluir esse cálculo.

Exercício$\PageIndex{4}$

Um bolo é retirado do forno depois de assado bem, e a temperatura do forno é$450°F$. A temperatura da cozinha é$70°F$, e depois de$10$ minutos a temperatura do bolo é$430°F$.

Escreva o problema de valor inicial apropriado para descrever essa situação.
Resolva o problema do valor inicial do$T(t)$.
Quanto tempo demorará até que a temperatura do bolo esteja dentro$5°F$ da temperatura ambiente?

Dica: Determine os valores de$T_s$ e$T_0$, em seguida, use a Equação\ ref {newton}.
Responda a: Problema de valor inicial\[\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber \]
Resposta b: \[T(t)=70+380e^{kt}\nonumber \]
Resposta c: Aproximadamente$114$ minutos.

Conceitos-chave

Uma equação diferencial separável é qualquer equação que possa ser escrita na forma$y'=f(x)g(y).$
O método de separação de variáveis é usado para encontrar a solução geral para uma equação diferencial separável.

Equações-chave

Equação diferencial separável

$y′=f(x)g(y)$

concentração da solução

$\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}$

Lei do resfriamento de Newton

$\dfrac{dT}{dt}=k(T−T_s)$

Glossário

equação diferencial autônoma: uma equação na qual o lado direito é uma função de$y$ sozinho

equação diferencial separável: qualquer equação que possa ser escrita na forma$y'=f(x)g(y)$

separação de variáveis: um método usado para resolver uma equação diferencial separável

Definição: Equações diferenciais separáveis

Estratégia de resolução de problemas: separação de variáveis

Exemplo\(\PageIndex{1}\): Using Separation of Variables

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Solving an Initial-Value Problem

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\): Determining Salt Concentration over Time

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): Waiting for a Pizza to Cool

Exercício\(\PageIndex{4}\)