8.2E: Exercícios para a Seção 8.2

Last updated
Save as PDF

Page ID: 188104

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para os exercícios 1 a 3, use o campo de direção abaixo da equação diferencial$ y'=−2y.$ Esboce o gráfico da solução para as condições iniciais dadas.

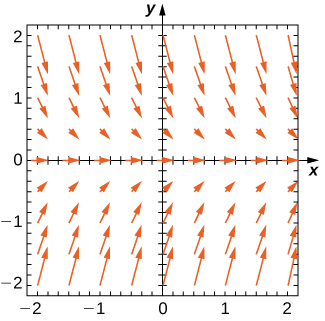
$Um campo de direção com setas horizontais apontando para a direita em 0. As setas acima do eixo x apontam para baixo e para a direita. Quanto mais longe do eixo x, mais íngremes são as setas, e quanto mais próximas do eixo x, mais planas são as setas. Da mesma forma, as setas abaixo do eixo x apontam para cima e para a direita. Quanto mais longe do eixo x, mais íngremes são as setas, e quanto mais próximas do eixo x, mais planas são as setas.$

1)$ y(0)=1$

2)$ y(0)=0$

Responda: 0. Quanto mais próximas elas estão do eixo x, mais horizontais são as setas, e quanto mais distantes elas estão, mais verticais elas se tornam." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_203.jpeg">

3)$ y(0)=−1$

4) Há algum equilíbrio entre as soluções da equação diferencial dos exercícios 1 - 3? Liste todos os equilíbrios junto com suas estabilidades.

Responda: $ y=0$é um equilíbrio estável

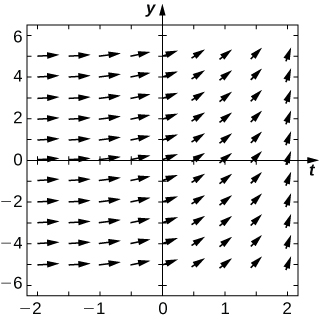
Para os exercícios 5 a 7, use o campo de direção abaixo da equação diferencial$ y'=y^2−2y$. Esboce o gráfico da solução para as condições iniciais dadas.

Um campo de direção com setas horizontais em y = 0 e y = 2. As setas apontam para y 2 e para y < 0. As setas apontam para baixo para 0 < y < 2. Quanto mais próximas as setas estiverem dessas linhas, mais horizontais elas serão e, quanto mais distantes, mais verticais serão as setas." style="width: 325px; height: 321px;" width="325px" height="321px" src="https://math.libretexts.org/@api/dek...08_02_205.jpeg">

5)$ y(0)=3$

6)$ y(0)=1$

Responda: 2 e para y < 0. As setas apontam para baixo para 0 < y < 2. Quanto mais próximas as setas estiverem dessas linhas, mais horizontais elas serão e, quanto mais distantes, mais verticais serão as setas. É esboçada uma solução que segue y = 2 no quadrante dois, passa por (0, 1) e segue o eixo x." style="width: 319px; height: 320px;" width="319px" height="320px" src="https://math.libretexts.org/@api/dek...08_02_207.jpeg">

7)$ y(0)=−1$

8) Há algum equilíbrio entre as soluções da equação diferencial dos exercícios 5 a 7? Liste todos os equilíbrios junto com suas estabilidades.

Responda: $ y=0$é um equilíbrio estável e$ y=2$ é instável

Nos exercícios 9 a 13, desenhe o campo de direção para as seguintes equações diferenciais e resolva a equação diferencial. Desenhe sua solução em cima do campo de direção. Sua solução segue as setas em seu campo de direção?

9)$ y'=t^3$

10)$ y'=e^t$

Responda: $Um campo de direção sobre os quatro quadrantes. À medida que t vai de 0 ao infinito, as setas se tornam cada vez mais verticais depois de ficarem horizontais mais próximas de x = 0.$

11)$ \dfrac{dy}{dx}=x^2\cos x$

12)$ \dfrac{dy}{dt}=te^t$

Responda: $Um campo de direção sobre [-2, 2] nos eixos x e y. As setas apontam ligeiramente para baixo e para a direita sobre [-2, 0] e gradualmente se tornam verticais sobre [0, 2].$

13)$ \dfrac{dx}{dt}=\cosh(t)$

Nos exercícios 14 a 18, desenhe o campo direcional para as seguintes equações diferenciais. O que você pode dizer sobre o comportamento da solução? Existem equilíbrios? Que estabilidade esses equilíbrios têm?

14)$ y'=y^2−1$

Responda: Parece haver equlibria em$y = -1$ (estável) e$y = 1$ (instável).
1. As setas apontam para baixo para -1 < y < 1. Quanto mais próximas as setas estão dessas linhas, mais horizontais elas são, e quanto mais distantes elas estão, mais verticais elas são." style="width: 342px; height: 344px;" width="342px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_214.jpeg">

15)$ y'=y−x$

16)$ y'=1−y^2−x^2$

Responda: Não parece haver nenhum equilíbrio.
$Um campo de direção com setas apontando para baixo e para a direita para quase todos os pontos em [-2, 2] nos eixos x e y. Perto da origem, as setas ficam mais horizontais, apontam para o canto superior direito, ficam mais horizontais e apontam para baixo novamente para a direita.$

17)$ y'=t^2\sin y$

18)$ y'=3y+xy$

Responda: Parece haver um equilíbrio instável em$y=0.$
-3, as setas apontam para cima. Abaixo do eixo x e para x < -3, as setas apontam para cima. Para x > -3, as setas apontam para baixo. Quanto mais longe do eixo x e x = -3, as setas se tornam mais verticais e, quanto mais próximas elas se tornam, mais horizontais elas se tornam." style="width: 405px; height: 344px;" width="405px" height="344px" src="https://math.libretexts.org/@api/dek...08_02_218.jpeg">

Combine o campo de direção com as equações diferenciais fornecidas. Explique suas seleções.

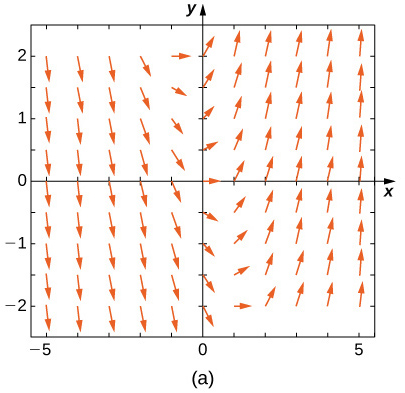
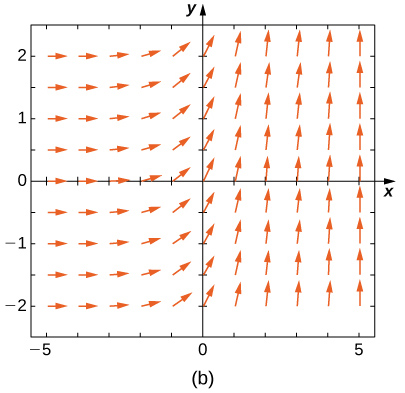
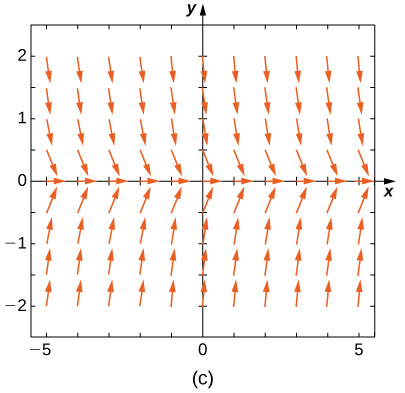
$Um campo de direção com setas apontando para baixo e para a direita nos quadrantes dois e três. Depois de cruzar o eixo y, as setas mudam de direção e apontam para a direita.$ $Um campo de direção com setas horizontais apontando para a esquerda nos quadrantes dois e três. Ao cruzar o eixo y, as setas alternam e apontam para cima nos quadrantes um e quatro.$ $Um campo de direção com setas horizontais apontando para a direita no eixo x. Acima, as setas apontam para baixo e para a direita, e abaixo, as setas apontam para cima e para a direita. 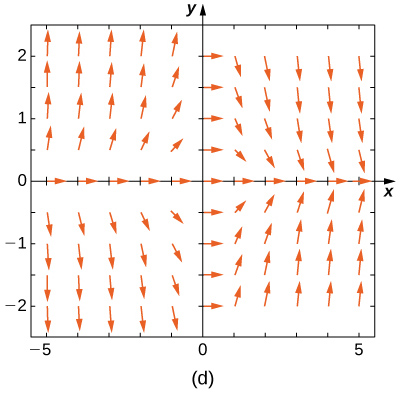Quanto mais longe do eixo x, mais verticais as setas se tornam.$ $Um campo de direção com setas horizontais nos eixos x e y. As setas apontam para baixo e para a direita nos quadrantes um e três. 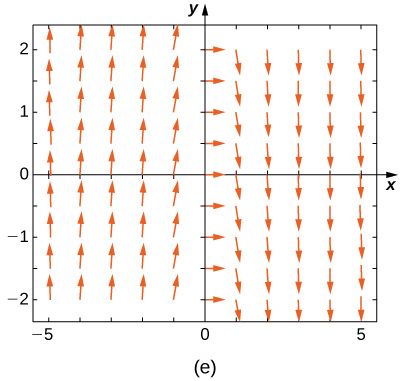Eles apontam para cima e para a direita nos quadrantes dois e quatro.$ $Um campo de direção com setas apontando para cima nos quadrantes dois e três, para a direita no eixo y e para baixo nos quadrantes um e quatro.$

19)$ y'=−3y$

20)$ y'=−3t$

Responda: $ E$

21)$ y'=e^t$

22)$ y'=\frac{1}{2}y+t$

Responda: $ A$

23)$ y'=−ty$

Combine o campo de direção com as equações diferenciais fornecidas. Explique suas seleções.

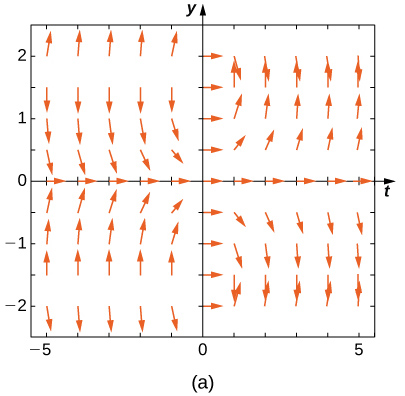
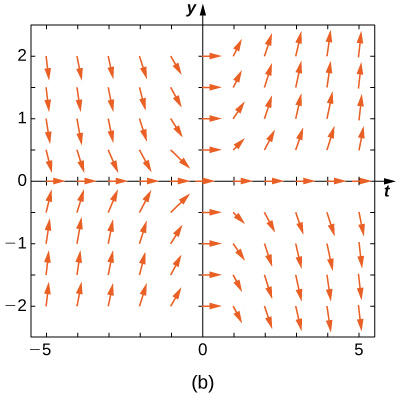
$Um campo de direção com setas horizontais apontando para a direita nos eixos x e y. Nos quadrantes um e três, as setas apontam para cima, e nos quadrantes dois e quatro, elas apontam para baixo.$ $Um campo de direção com setas horizontais apontando para a direita nos eixos x e y. 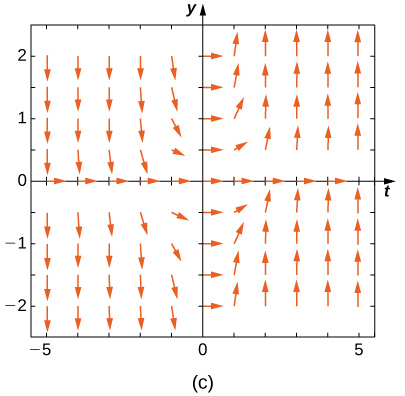Nos quadrantes um e três, as setas apontam para cima e para a direita, e nos quadrantes dois e quatro, as setas apontam para baixo e para a direita.$ $Um campo de direção com setas horizontais apontando para a direita nos eixos x e y. 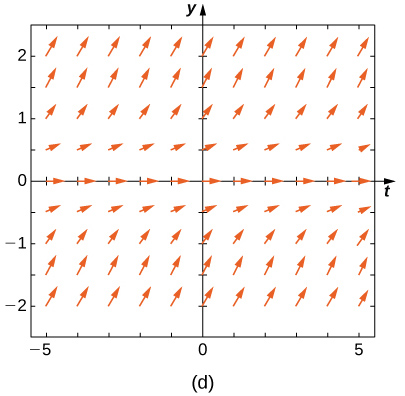Nos quadrantes dois e três, as setas apontam para baixo, e nos quadrantes um e quatro, as setas apontam para cima.$ $Um campo de direção com setas horizontais apontando para a direita no eixo x. As setas apontam para cima e para a direita em todos os quadrantes. Quanto mais próximas as setas estiverem do eixo x, mais horizontais serão as setas e, quanto mais distantes estiverem, mais verticais elas serão.$ 1,5 e x < 0, para y < -1,5 e x < 0 e para -1,5 < y < 1.5 and x > 0-, as setas apontam para baixo. Para y> 1,5 e x > 0, para y < -1,5, para y < -1.5 and x > 0 e para -1,5 < y < 1,5 e x < 0, as setas apontam para cima." style="width: 405px; height: 380px;" width="405px" height="380px" src="https://math.libretexts.org/@api/dek...8_02_220e.jpeg">

24)$ y'=t\sin y$

Responda: $ B$

25)$ y'=−t\cos y$

26)$ y'=t\tan y$

Responda: $ A$

27)$ y'=\sin^2y$

28)$ y'=y^2t^3$

Responda: $ C$

Faça uma estimativa das seguintes soluções usando o método de Euler com$ n=5$ etapas ao longo do intervalo.$ t=[0,1].$ Se você conseguir resolver o problema do valor inicial com exatidão, compare sua solução com a solução exata. Se você não conseguir resolver o problema do valor inicial, a solução exata será fornecida para você comparar com o método de Euler. Quão preciso é o método de Euler?

29)$ y'=−3y,\quad y(0)=1$

30)$ y'=t^2,\quad y(0)=1$

Responda: $ 2.24,$exato:$ 3$

Solução:

31)$ y′=3t−y,\quad y(0)=1.$ A solução exata é$ y=3t+4e^{−t}−3$

32)$ y′=y+t^2,\quad y(0)=3.$ A solução exata é$ y=5e^t−2−t^2−2t$

Responda: $ 7.739364,$exato:$ 5(e−1)$

33)$ y′=2t,\quad y(0)=0$

34) [T]$ y'=e^{x+y},y(0)=−1.$ A solução exata é$ y=−\ln(e+1−e^x)$

Responda: $ −0.2535,$exato:$ 0$

35)$ y′=y^2\ln(x+1),\quad y(0)=1.$ A solução exata é$ y=−\dfrac{1}{(x+1)(\ln(x+1)−1)}$

36)$ y′=2^x,\quad y(0)=0.$ A solução exata é$ y=\dfrac{2^x−1}{\ln 2}$

Responda: $ 1.345,$exato:$ \frac{1}{\ln(2)}$

37)$ y′=y,\quad y(0)=−1.$ A solução exata é$ y=−e^x$.

38)$ y′=−5t,\quad y(0)=−2.$ A solução exata é$ y=−\frac{5}{2}t^2−2$

Responda: $ −4,$exato:$ −1/2$

Equações diferenciais podem ser usadas para modelar epidemias de doenças. No próximo conjunto de problemas, examinamos a mudança de tamanho de duas subpopulações de pessoas que vivem em uma cidade: indivíduos infectados e indivíduos suscetíveis à infecção. $ S$representa o tamanho da população suscetível e$ I$ representa o tamanho da população infectada. Assumimos que, se uma pessoa suscetível interage com uma pessoa infectada, há uma probabilidade de$ c$ que a pessoa suscetível seja infectada. Cada pessoa infectada se recupera da infecção rapidamente$ r$ e se torna suscetível novamente. Consideramos o caso da gripe, onde assumimos que ninguém morre por causa da doença, então assumimos que o tamanho total da população das duas subpopulações é um número constante,$ N$. As equações diferenciais que modelam esses tamanhos populacionais são

$ S'=rI−cSI$e$ I'=cSI−rI.$

Aqui$ c$ representa a taxa de contato e$ r$ a taxa de recuperação.

39) Mostre que, assumindo que o tamanho total da população é constante,$ (S+I=N),$ você pode reduzir o sistema a uma única equação diferencial em$ I:I'=c(N−I)I−rI.$

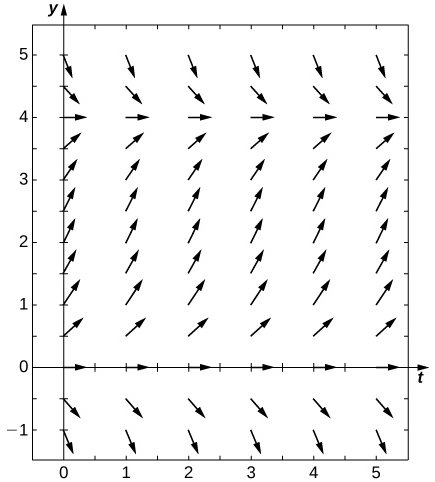
40) Supondo que os parâmetros sejam$ c=0.5,N=5,$ e$ r=0.5$, desenhe o campo direcional resultante.

Responda: $Um campo de direção com setas horizontais apontando para a direita no eixo x e em y = 4. As setas abaixo do eixo x e acima de y = 4 apontam para baixo e para a direita. As setas entre o eixo x e y = 4 apontam para cima e para a direita.$

41) [T] Use um software computacional ou uma calculadora para calcular a solução para o problema do valor inicial$ y'=ty,y(0)=2$ usando o Método de Euler com o tamanho do passo fornecido$ h$. Encontre a solução em$ t=1$. Para uma dica, aqui está o “pseudocódigo” de como escrever um programa de computador para executar o Método de Euler para$ y'=f(t,y),y(0)=2:$

Criar função$ f(t,y)$

Defina os parâmetros$ h$, tamanho da$ y(1)=y_0,t(0)=0,$ etapa e número total de etapas,$ N$

Escreva um for-loop:

para$ k=1$ dois$ N$

$ fn=f(t(k),y(k))$

$ y(k+1)=y(k)+h*fn$

$ t(k+1)=t(k)+h$

42) Resolva o problema do valor inicial para obter a solução exata.

Responda: $ y'=2e^{t^2/2}$

43) Desenhe o campo direcional

44)$ h=1$

Responda: $ 2$

45) [T]$ h=10$

46) [T]$ h=100$

Responda: $ 3.2756$

47) [T]$ h=1000$

48) [T] Avalie a solução exata em$ t=1$. Faça uma tabela de erros para o erro relativo entre a solução do método de Euler e a solução exata. Quanto o erro muda? Você pode explicar?

Responda

Solução exata: y =$ 2\sqrt{e}.$

Tamanho da etapa	Erro
$ h=1$	$ 0.3935$
$ h=10$	$ 0.06163$
$ h=100$	$ 0.006612$
$ h=10000$	$ 0.0006661$

Para os exercícios 49 a 53, considere o problema do valor inicial$ y'=−2y,$ com$y(0)=2.$

49) Mostre que$ y=2e^{−2x}$ resolve esse problema de valor inicial.

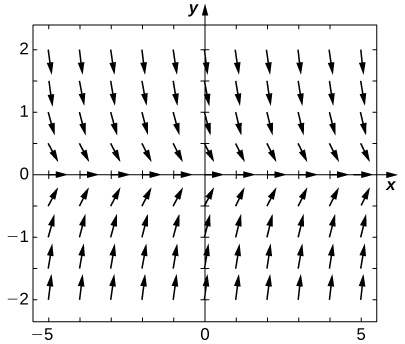
50) Desenhe o campo direcional dessa equação diferencial.

Responda: $Campo de direção para a equação diferencial y' = -2y. Um campo de direção com setas horizontais apontando para a direita no eixo x. Acima do eixo x, as setas apontam para baixo e para a direita. Abaixo do eixo x, as setas apontam para cima e para a direita. Quanto mais próximas as setas estiverem do eixo x, mais horizontais serão as setas e, quanto mais distantes estiverem do eixo x, mais verticais serão as setas.$

51) [T] À mão ou por calculadora ou computador, aproxime a solução usando o Método de Euler$ h=5$.$ t=10$

52) [T] Por calculadora ou computador, aproxime a solução usando o Método de Euler em$ t=10$ usar$ h=100.$

Responda: $ 4.0741e^{−10}$

53) [T] Faça um gráfico da resposta exata e de cada aproximação de Euler (para$ h=5$ e$ h=100$) a cada h no campo direcional. O que você percebe?

Tamanho da etapa	Erro
\( h=1\)	\( 0.3935\)
\( h=10\)	\( 0.06163\)
\( h=100\)	\( 0.006612\)
\( h=10000\)	\( 0.0006661\)