8.2: Campos de direção e métodos numéricos

Last updated
Save as PDF

Page ID: 188091

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Desenhe o campo de direção para uma determinada equação diferencial de primeira ordem.
Use um campo de direção para desenhar uma curva de solução de uma equação diferencial de primeira ordem.
Use o Método de Euler para aproximar a solução de uma equação diferencial de primeira ordem.

No restante deste capítulo, vamos nos concentrar em vários métodos para resolver equações diferenciais e analisar o comportamento das soluções. Em alguns casos, é possível prever as propriedades de uma solução para uma equação diferencial sem conhecer a solução real. Também estudaremos métodos numéricos para resolver equações diferenciais, que podem ser programados usando várias linguagens de computador ou até mesmo usando um programa de planilhas, como o Microsoft Excel.

Criando campos de direção

Os campos de direção (também chamados de campos de inclinação) são úteis para investigar equações diferenciais de primeira ordem. Em particular, consideramos uma equação diferencial de primeira ordem da forma

\[ y'=f(x,y).\nonumber \]

Um exemplo aplicado desse tipo de equação diferencial aparece na lei de resfriamento de Newton, que resolveremos explicitamente mais adiante neste capítulo. Primeiro, porém, vamos criar um campo de direção para a equação diferencial

\[ T′(t)=−0.4(T−72).\nonumber \]

Aqui$ T(t)$ representa a temperatura (em graus Fahrenheit) de um objeto no momento$ t$, e a temperatura ambiente é$ 72°F$. A figura$ \PageIndex{1}$ mostra o campo de direção para essa equação.

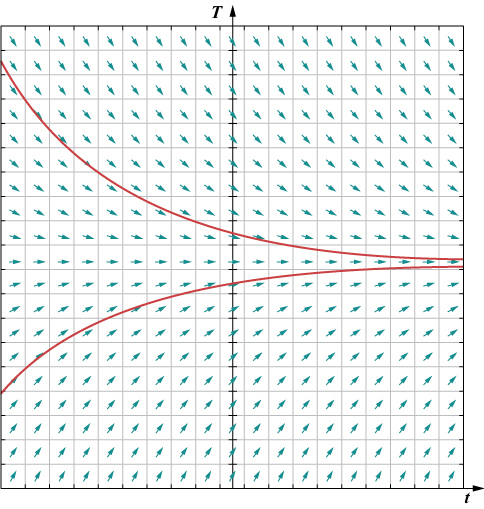
Um gráfico de um campo de direção para a equação diferencial dada nos quadrantes um e dois. As setas estão apontando diretamente para a direita em y = 72. Abaixo dessa linha, as setas têm uma inclinação cada vez mais positiva à medida que y se torna menor. Acima dessa linha, as setas têm uma inclinação cada vez mais negativa à medida que y se torna maior. As setas apontam para a convergência em y = 72. Duas soluções são desenhadas: uma para temperatura inicial menor que 72 e outra para temperaturas iniciais maiores que 72. A solução superior é uma curva ascendente côncava decrescente, aproximando-se de y = 72 à medida que t vai para o infinito. A solução inferior é uma curva descendente côncava crescente, aproximando-se de y = 72 à medida que t vai para o infinito. — Figura$ \PageIndex{1}$: Campo de direção para a equação diferencial$ T′(t)=−0.4(T−72)$. Duas soluções são plotadas: uma com temperatura inicial menor que$ 72°F$ e outra com temperatura inicial maior que$ 72°F$.

A ideia por trás de um campo de direção é o fato de que a derivada de uma função avaliada em um determinado ponto é a inclinação da reta tangente ao gráfico dessa função no mesmo ponto. Outros exemplos de equações diferenciais para as quais podemos criar um campo de direção incluem

\[ y'=3x+2y−4\nonumber \]

\[ y'=x^2−y^2\nonumber \]

\[ y'=\frac{2x+4}{y−2}.\nonumber \]

Para criar um campo de direção, começamos com a primeira equação:$ y'=3x+2y−4$. Deixamos$ \left(x_0,\, y_0\right)$ ser qualquer par ordenado e substituímos esses números no lado direito da equação diferencial. Por exemplo, se escolhermos$ x=1$ e$ y=2$, substituindo no lado direito da equação diferencial, produzimos

$ y′=3x+2y−4=3(1)+2(2)−4=3.$

Isso nos diz que, se uma solução para a equação diferencial$ y'=3x+2y−4$ passar pelo ponto$ (1,2)$, a inclinação da solução nesse ponto deve ser igual a 3. Para começar a criar o campo de direção, colocamos um segmento de linha curta no ponto$ (1,2)$ com inclinação$ 3$. Podemos fazer isso para qualquer ponto no domínio da função$ f(x,y)=3x+2y−4,$ que consiste em todos os pares ordenados$ (x,y)$ em$ R^2$. Portanto, qualquer ponto no plano cartesiano tem uma inclinação associada a ele, assumindo que uma solução para a equação diferencial passa por esse ponto. O campo de direção da equação diferencial$ y′=3x+2y−4$ é mostrado na Figura$ \PageIndex{2}$.

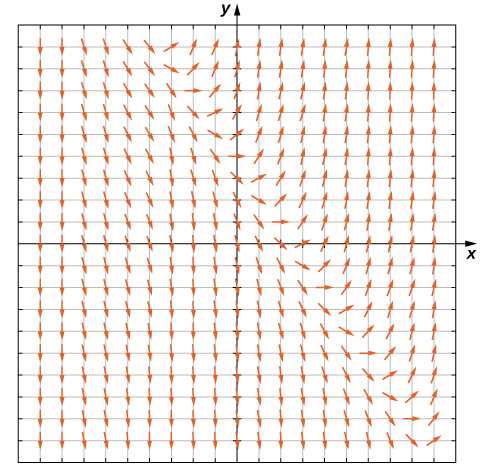
Um gráfico do campo de direção da equação diferencial y' = 3 x + 2 y — 4 em todos os quatro quadrantes. Nos quadrantes dois e três, as setas apontam para baixo e ligeiramente para a direita. Em uma linha diagonal, aproximadamente y = -x + 2, as setas apontam cada vez mais para a direita, se curvam e apontam para cima acima dessa linha. — Figura$ \PageIndex{2}$: Campo de direção para a equação diferencial$ y'=3x+2y−4$.

Podemos gerar um campo de direção desse tipo para qualquer equação diferencial da forma$ y'=f(x,y).$

Definição: Campo de direção (campo de inclinação)

Um campo de direção (campo de inclinação) é um objeto matemático usado para representar graficamente soluções para uma equação diferencial de primeira ordem. Em cada ponto em um campo de direção, aparece um segmento de linha cuja inclinação é igual à inclinação de uma solução para a equação diferencial que passa por esse ponto.

Usando campos de direção

Podemos usar um campo de direção para prever o comportamento das soluções para uma equação diferencial sem conhecer a solução real. Por exemplo, o campo de direção na Figura$ \PageIndex{3}$ serve como um guia para o comportamento das soluções para a equação diferencial$ y'=3x+2y−4.$

Para usar um campo de direção, começamos escolhendo qualquer ponto no campo. O segmento de linha nesse ponto serve como uma placa de sinalização nos dizendo em que direção seguir a partir daí. Por exemplo, se uma solução para a equação diferencial passa pelo ponto$ (0,1),$, então a inclinação da solução que passa por esse ponto é dada por$ y'=3(0)+2(1)−4=−2.$ Agora, vamos$ x$ aumentar ligeiramente, digamos para$ x=0.1$. O uso do método de aproximações lineares fornece uma fórmula para o valor aproximado de$ y$ para$ x=0.1.$ Em particular,

\[ L(x)=y_0+f′(x_0)(x−x_0)=1−2(x_0−0)=1−2x_0.\nonumber \]

Substituir$ x_0=0.1$ em$ L(x)$ fornece um$ y$ valor aproximado de$ 0.8$.

Nesse ponto, a inclinação da solução muda (novamente de acordo com a equação diferencial). Podemos continuar progredindo, recalculando a inclinação da solução à medida que damos pequenos passos para a direita e observando o comportamento da solução. A figura$ \PageIndex{3}$ mostra um gráfico da solução passando pelo ponto$ (0,1)$.

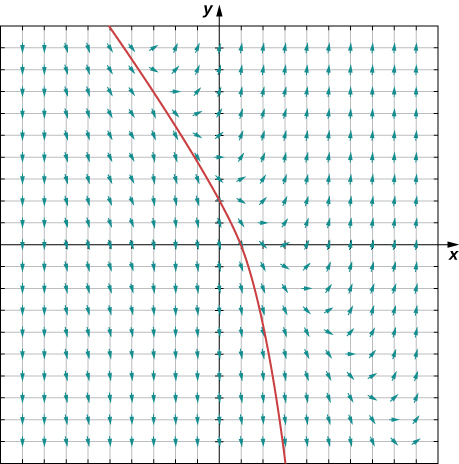
A curva é o gráfico da solução para o problema do valor inicial

\[ y'=3x+2y−4,\; y(0)=1.\nonumber \]

Essa curva é chamada de curva de solução passando pelo ponto.$ (0,1).$ A solução exata para esse problema de valor inicial é

\[ y=−\frac{3}{2}x+\frac{5}{4}−\frac{1}{4}e^{2x},\nonumber \]

e o gráfico dessa solução é idêntico à curva na Figura$ \PageIndex{3}$.

Exercício$\PageIndex{1}$

Crie um campo de direção para a equação diferencial$ y'=x^2−y^2$ e desenhe uma curva de solução passando pelo ponto$ (−1,2)$.

Dica: Uso$ x$ e$ y$ valores que variam$ −5$ de$ 5$ a. Para cada par de coordenadas, calcule$ y'$ usando o lado direito da equação diferencial.

Resposta: $Um gráfico do campo de direção da equação diferencial y' = x ^ 2 — y ^ 2. Ao longo de y = x e y = -x, as linhas são horizontais. Em ambos os lados de y = x e y = -x, as linhas inclinam e direcionam soluções ao longo dessas duas funções. O resto das linhas são verticais. A solução que está passando por (-1, 2) é mostrada. Ele se curva para baixo de cerca de (-2,75, 10), passando por (-1, 2) e cerca de (0, 1,5) e, em seguida, para cima ao longo da diagonal até (10, 10).$

Agora, considere o campo de direção para a equação diferencial$ y'=(x−3)(y^2−4)$, mostrado na Figura$ \PageIndex{4}$. Esse campo de direção tem várias propriedades interessantes. Em primeiro lugar, em$ y=−2$ e$ y=2$, traços horizontais aparecem em todo o gráfico. Isso significa que se$ y=−2$, então,$ y'=0.$ substituir essa expressão no lado direito da equação diferencial, obtém-se

\ [\ begin {align*} (x−3) (y^2−4) &= (x−3) ((−2) ^2−4)\ [4pt]
& =( x−3) (0)\\ [4pt]
&=0\\ [4pt]
&=y'. \ end {align*}\]

Portanto,$ y=−2$ é uma solução para a equação diferencial. Da mesma forma,$ y=2$ é uma solução para a equação diferencial. Essas são as únicas soluções de valor constante para a equação diferencial, como podemos ver no argumento a seguir. Suponha que$ y=k$ seja uma solução constante para a equação diferencial. Então$ y′=0$. Substituir essa expressão na equação diferencial produz$ 0=(x−3)(k^2−4)$. Essa equação deve ser verdadeira para todos os valores de$ x$, então o segundo fator deve ser igual a zero. Esse resultado produz a equação$ k^2−4=0$. As soluções para essa equação são$ k=−2$ e$ k=2$, que são as soluções constantes já mencionadas. Essas são chamadas de soluções de equilíbrio para a equação diferencial.

Um campo de direção para a equação diferencial dada. As setas são horizontais e apontam para a direita em y = -2, y = 2 e x = 3. Quanto mais próximas as setas estiverem de x = 6, mais horizontais as setas se tornarão. Quanto mais distantes, mais verticais elas ficam. — Figura$ \PageIndex{4}$: Campo de direção para a equação diferencial$ y'=(x−3)(y^2−4)$ mostrando duas soluções. Essas soluções estão muito próximas, mas uma está pouco acima da solução de equilíbrio$ x=−2$ e a outra está pouco abaixo da mesma solução de equilíbrio.

Definição: E quilibrium Solutions

Considere a equação diferencial$ y'=f(x,y)$. Uma solução de equilíbrio é qualquer solução para a equação diferencial da forma$ y=c$, onde$c$ é uma constante.

Para determinar as soluções de equilíbrio para a equação diferencial$ y'=f(x,y)$, defina o lado direito igual a zero. Uma solução de equilíbrio da equação diferencial é qualquer função da forma$ y=k$ tal que$ f(x,k)=0$ para todos os valores de$ x$ no domínio de$ f$.

Uma característica importante das soluções de equilíbrio diz respeito ao fato de elas abordarem ou não a linha$ y=k$ como uma assíntota para grandes valores de$ x$.

Definição: soluções assintoticamente estáveis, instáveis e semi-estáveis

Considere a equação diferencial$ y′=f(x,y),$ e suponha que todas as soluções para essa equação diferencial estejam definidas para$ x≥x_0$. $ y=k$Seja uma solução de equilíbrio para a equação diferencial.

$ y=k$é uma solução assintoticamente estável para a equação diferencial, se existir, de$ ε>0$ tal forma que, para qualquer valor,$ c∈(k−ε,\, k+ε)$ a solução para o problema do valor inicial$ y′=f(x,y), \; y(x_0)=c$ se$ k$ aproxime ao infinito.$ x$
$ y=k$é uma solução assintoticamente instável para a equação diferencial, se existir$ ε>0$ tal que, para qualquer valor,$ c∈(k−ε,\, k+ε)$ a solução para o problema do valor inicial$ y′=f(x,y), \; y(x_0)=c$ nunca se aproxime$ k$ quando$ x$ se aproxima do infinito.
$ y=k$é uma solução assintoticamente semi-estável para a equação diferencial se não for assintoticamente estável nem assintoticamente instável.

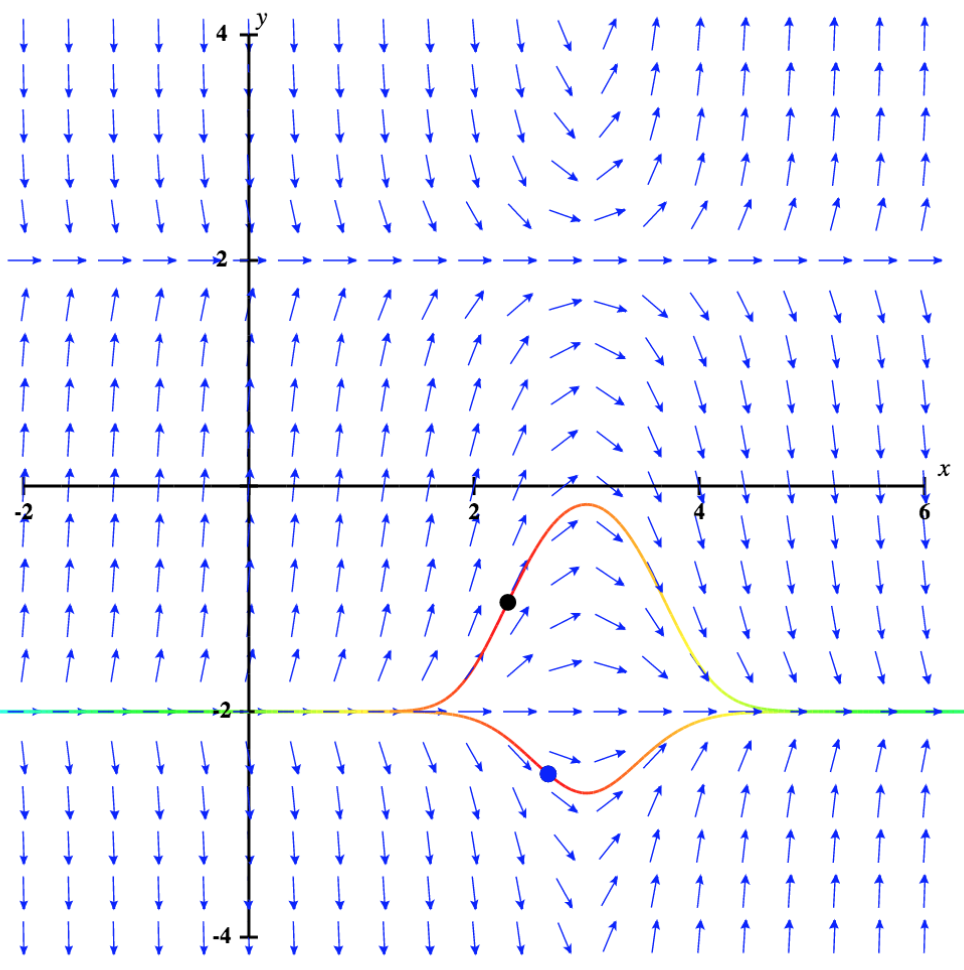
Agora retornamos à equação diferencial$ y'=(x−3)(y^2−4)$, com a condição inicial$ y(0)=0.5$. O campo de direção para esse problema de valor inicial, junto com a solução correspondente, é mostrado na Figura$ \PageIndex{5}$.

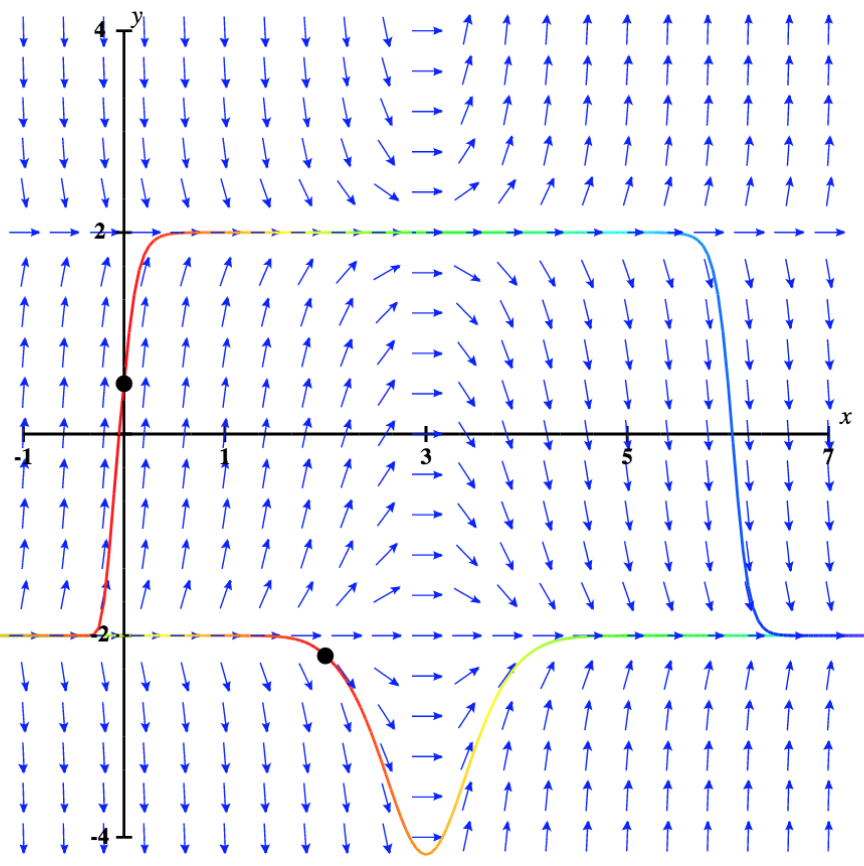
Um campo de direção para a equação diferencial dada. As setas são horizontais e apontam para a direita em y = -2, y = 2 e x = 3. É representada graficamente uma solução que passa por (0, 0,5) e outra pelo ponto (2, -2,2). Ambas as curvas eventualmente se aproximam da linha y = -2 de forma assintotica.. — Figura$ \PageIndex{5}$: Campo de direção para o problema do valor inicial$ y'=(x−3)(y^2−4),\; y(0)=0.5.$ Uma segunda curva de solução é representada graficamente com a condição inicial$(2, -2.2)$.

Os valores da solução para esse problema de valor inicial permanecem entre$ y=−2$ e$ y=2$, que são as soluções de equilíbrio para a equação diferencial. Além disso, à medida que$ x$ se aproxima do infinito, embora inicialmente pareçam se aproximar da linha y = 2, as$ y$ coordenadas -se aproximam claramente$ -2$. O comportamento das soluções é semelhante se o valor inicial estiver abaixo$ -2$, por exemplo,$ y(2)=-2.2$. Nesse caso, as soluções aumentam e se aproximam à$ y=-2$ medida que$ x$ se aproximam do infinito. Portanto,$ y=-2$ é uma solução assintoticamente estável para essa equação diferencial.

O que acontece quando o valor inicial está acima$ y=2$? Esse cenário é ilustrado na Figura$ \PageIndex{6}$, com o valor inicial$ y(0)=3.$

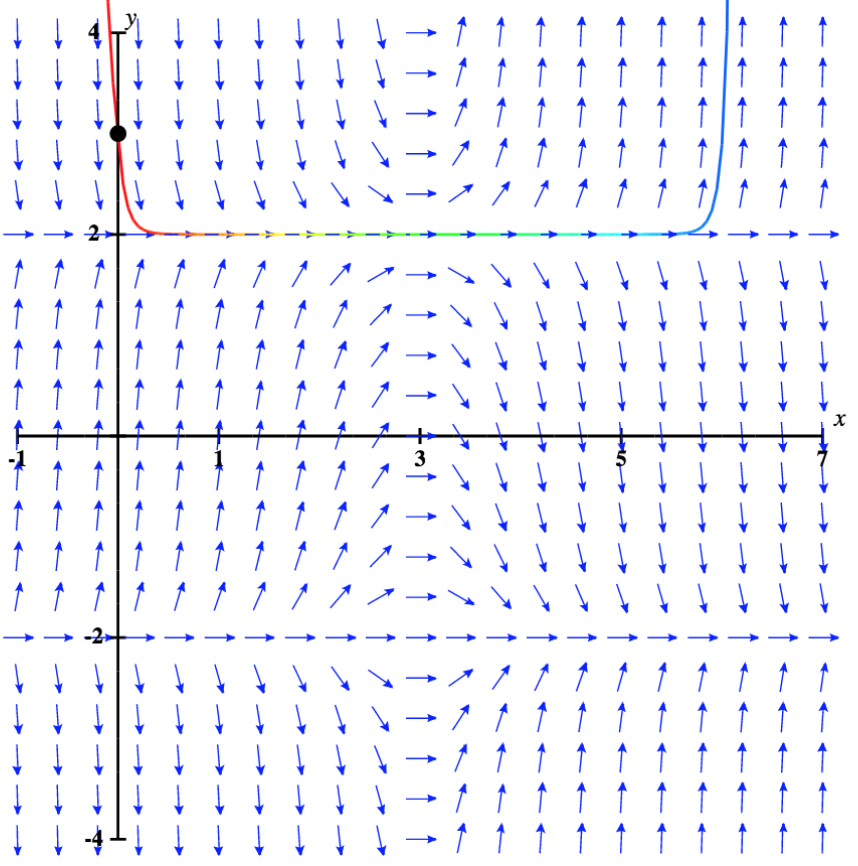
A solução aumenta rapidamente em direção ao infinito positivo à medida que$ x$ se aproxima do infinito. Além disso, se o valor inicial estiver um pouco abaixo$ 2$, a solução se aproxima$ -2$, que é a outra solução de equilíbrio. Portanto, em nenhum dos casos a solução se aproxima$ y=2$, então$ y=2$ é chamada de solução de equilíbrio assintoticamente instável ou instável.

Exemplo$ \PageIndex{1}$: Stability of an Equilibrium Solution

Crie um campo de direção para a equação diferencial$ y'=(y−3)^2(y^2+y−2)$ e identifique quaisquer soluções de equilíbrio. Classifique cada uma das soluções de equilíbrio como estável, instável ou semiestável.

Solução

O campo de direção é mostrado na Figura$ \PageIndex{7}$.

Um gráfico de um campo de direção com setas apontando para a direita em y = -4, y = 2 e y = 6. Para y < -4, as setas apontam para cima. Para -4 < y < 2, as setas apontam para baixo. Para 2 < y <6, as setas apontam para cima, tornando-se cada vez mais planas à medida que se aproximam de y = 6. Para y — Figura$ \PageIndex{7}$: Campo de direção para a equação diferencial$ y'=(y−3)^2(y^2+y−2).$

As soluções de equilíbrio são$ y=−2,\, y=1,$$ y=3$ e. Para classificar cada uma das soluções, observe uma seta diretamente acima ou abaixo de cada um desses valores. Por exemplo,$ y=−2$ nas setas diretamente abaixo dessa solução apontam para cima e as setas diretamente acima da solução apontam para baixo. Portanto, todas as condições iniciais se$ y=−2$ aproximam$ y=−2$ e a solução é estável. Para a solução$ y=1$, todas as condições iniciais acima e abaixo$ y=1$ são repelidas (afastadas)$ y=1$, portanto, essa solução é instável. A solução$ y=3$ é semiestável, porque para condições iniciais um pouco maiores que$ 3$, a solução se aproxima do infinito e, para condições iniciais um pouco menores que$ 3$, a solução se aproxima$ y=1$.

Análise

É possível encontrar as soluções de equilíbrio para a equação diferencial definindo o lado direito igual a zero e resolvendo para$ y.$ Essa abordagem fornece as mesmas soluções de equilíbrio que as que vimos no campo de direção.

Exercício$\PageIndex{2}$

Crie um campo de direção para a equação diferencial$ y'=(x+5)(y+2)(y^2−4y+4)$ e identifique quaisquer soluções de equilíbrio. Classifique cada uma das soluções de equilíbrio como estável, instável ou semiestável.

Dica: Primeiro, crie o campo de direção e procure traços horizontais que percorram toda a extensão. Em seguida, examine as linhas de inclinação diretamente acima e abaixo das soluções de equilíbrio.

Resposta

As soluções de equilíbrio são$ y=−2$$ y=2$ e. Para esta equação,$ y=−2$ é uma solução de equilíbrio instável e$ y=2$ é uma solução de equilíbrio semiestável.

Um campo de direção com setas apontando para a direita em y = -4 e y = 4. As setas apontam para cima para y -4 e para baixo para y < -4. Perto de y = 4, as setas são mais horizontais, mas quanto mais distantes, mais verticais elas se tornam." src="https://math.libretexts.org/@api/dek...2452/8.2.3.png">

Método de Euler

Considere o problema do valor inicial

\[ y′=2x−3,\;y(0)=3.\nonumber \]

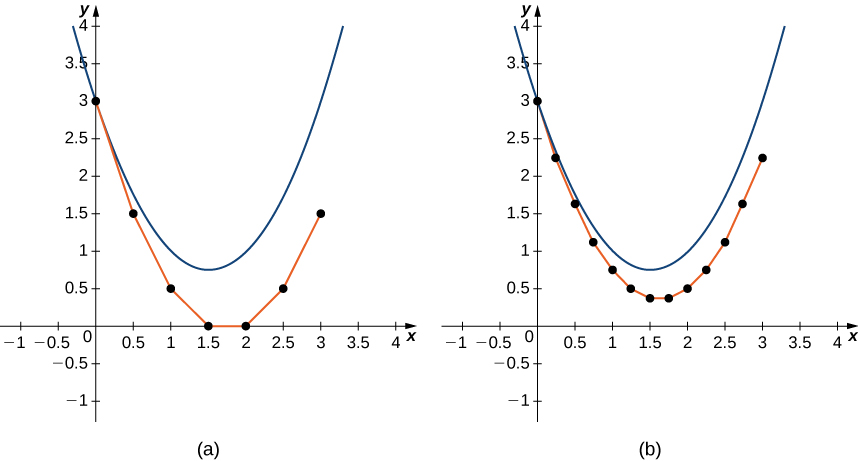
Integrar os dois lados da equação diferencial fornece$ y=x^2−3x+C,$ e resolvendo$ C$ rende a solução específica.$ y=x^2−3x+3.$ A solução para esse problema de valor inicial aparece como a parábola na Figura$ \PageIndex{8}$.

Um gráfico no intervalo [-1,4] para x e y. A parábola de abertura ascendente fornecida é desenhada com o vértice em (1,5, 0,75). Os pontos individuais são plotados em (0, 3), (0,5, 1,5), (1, 0,5), (1,5, 0), (2, 0), (2,5, 0,5) e (3, 1,5) com segmentos de linha conectando-os. — Figura$ \PageIndex{8}$: Método de Euler para o problema do valor inicial$ y′=2x−3,y(0)=3.$

O gráfico vermelho consiste em segmentos de linha que aproximam a solução do problema do valor inicial. O gráfico começa com o mesmo valor inicial de$ (0,3)$. Em seguida, a inclinação da solução em qualquer ponto é determinada pelo lado direito da equação diferencial, e o comprimento do segmento de linha é determinado aumentando o$ x$ valor a$ 0.5$ cada vez (o tamanho do passo). Essa abordagem é a base do Método de Euler.

Antes de declararmos o Método de Euler como um teorema, vamos considerar outro problema de valor inicial:

\[ y′=x^2−y^2,\; y(−1)=2.\nonumber \]

A ideia por trás dos campos de direção também pode ser aplicada a esse problema para estudar o comportamento de sua solução. Por exemplo, no ponto em que$ (−1,2),$ a inclinação da solução é dada por$ y'=(−1)^2−2^2=−3$, então a inclinação da reta tangente à solução nesse ponto também é igual$ −3$ a. Agora definimos$ x_0=−1$$ y_0=2$ e. Como a inclinação da solução neste ponto é igual a$ −3$, podemos usar o método de aproximação linear para aproximar y perto$ (−1,2)$.

\[ L(x)=y_0+f′(x_0)(x−x_0).\nonumber \]

Aqui$ x_0=−1,y_0=2,$ e$ f′(x_0)=−3,$ assim a aproximação linear se torna

\[ L(x)=2−3(x−(−1))=2−3x−3=−3x−1.\nonumber \]

Agora, escolhemos um tamanho de etapa. O tamanho da etapa é um valor pequeno, normalmente$ 0.1$ ou menor, que serve como um incremento para$ x$; é representado pela variável$ h$. Em nosso exemplo, vamos$ h=0.1$. Incrementar$ x_0$ em$ h$ dá nosso próximo$ x$ valor:

\[ x_1=x_0+h=−1+0.1=−0.9.\nonumber \]

Podemos substituir$ x_1=−0.9$ a aproximação linear para calcular$ y_1$.

\[ y_1=L(x_1)=−3(−0.9)−1=1.7.\nonumber \]

Portanto, o$ y$ valor aproximado da solução quando$ x=−0.9$ é$ y=1.7$. Podemos então repetir o processo, usando$ x_1=−0.9$ e$ y_1=1.7$ para calcular$ x_2$$ y_2$ e. A nova inclinação é dada por$ y'=(−0.9)^2−(1.7)^2=−2.08.$ First,$ x_2=x_1+h=−0.9+0.1=−0.8.$ Usando aproximação linear dá

\ (\ begin {align*} L (x) &=y_1+f′( x_1) (x−x_1)\\ [4pt]
&=1,7−2,08 (x− (−0,9))\ [4pt]
&=1,7−2,08x−1,872\\ [4pt]
&=−2,08x−0,172. \ end {align*}\)

Finalmente, substituímos$ x_2=−0.8$ a aproximação linear para calcular$ y_2$.

\ (\ begin {align*} Y_2&=L (x_2)\\ [4pt]
&=−2,08x_2−0,172\\ [4pt]
&=−2,08 (−0,8) −0,172\\ [4pt]
&=1,492. \ end {align*}\)

Portanto, o valor aproximado da solução para a equação diferencial é$ y=1.492$ quando$ x=−0.8.$

O que acabamos de mostrar é a ideia por trás do Método de Euler. A repetição dessas etapas fornece uma lista de valores para a solução. Esses valores são mostrados na tabela, arredondados para quatro casas decimais.

Tabela$ \PageIndex{1}$: Usando o método de Euler para aproximar soluções para uma equação diferencial
$ n$	0	1	2	3	4	5
$ x_n$	−1	−0,9	−0,8	−0,7	−0,6	−0,5
$ y_n$	2	1.7	1.492	1.334	1.2046	1,0955
$ n$	6	7	8	9	10
$ x_n$	−0,4	−0,3	−0,2	−0,1	0
$ y_n$	1.0004	1.9164	1.8414	1.746	1.7156

Método de Euler

Considere o problema do valor inicial

\[ y'=f(x,y),\; y(x_0)=y_0.\nonumber \]

Para aproximar uma solução para esse problema usando o método de Euler, defina

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$.

Aqui$ h>0$ representa o tamanho da etapa e$ n$ é um número inteiro, começando com$ 1$. O número de passos dados é contado pela variável$ n$.

Normalmente$ h$ é um valor pequeno, digamos$ 0.1$ ou$ 0.05$. Quanto menor o valor de$ h$, mais cálculos são necessários. Quanto maior o valor de$ h$, menos cálculos são necessários. No entanto, a compensação resulta em um menor grau de precisão para um tamanho de degrau maior, conforme ilustrado na Figura$ \PageIndex{9}$.

Dois gráficos da mesma parábola, y = x ^ 2 — 3 x + 3. O primeiro mostra o método de Euler para o problema do valor inicial fornecido com um tamanho de passo de h = 0,05, e o segundo mostra o método de Euler com um tamanho de passo de h = 0,25. O primeiro então tem os pontos (0, 3), (0,5, 1,5), (1, 0,5), (1,5, 0), (2, 0), (2,5, 0,5) e (3, 1,5) plotados com segmentos de linha conectando-os. O segundo tem os pontos (0, 3), (0,25, 2,25), (0,5, 1,625), (0,75, 1,125), (1, 0,75), (1,25, 0,5), (1,5, 0,375), (2, 0,5), (2,25, 0,75), (2,5, 1,125), (2,75, 1,625) e (3, 2,25) plpontilhados com segmentos de linha conectando-os. — Figura$ \PageIndex{9}$: Método de Euler para o problema do valor inicial$ y′=2x−3,\; y(0)=3$ com (a) um tamanho de etapa de$ h=0.5$; e (b) um tamanho de etapa de$ h=0.25.$

Exemplo$ \PageIndex{2}$: Using Euler’s Method

Considere o problema do valor inicial

\[ y′=3x^2−y^2+1,\; y(0)=2.\nonumber \]

Use o método de Euler com um tamanho de etapa de$ 0.1$ para gerar uma tabela de valores para a solução para valores$ x$ entre$ 0$$ 1$ e.

Solução

Recebemos$ h=0.1$ e,$ f(x,y)=3x^2−y^2+1.$ além disso, a condição inicial$ y(0)=2$ dá$ x_0=0$$ y_0=2$ e. Usando a Equação com$ n=0$, podemos gerar essa tabela.

Tabela$ \PageIndex{2}$: Usando o método de Euler para aproximar soluções para uma equação diferencial
$ n$	$ x_n$	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
\ (n\)” style="alinhamento vertical: médio; ">0	\ (x_n\)” style="alinhamento vertical: médio; ">0	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">2
\ (n\)” style="alinhamento vertical: médio; ">1	\ (x_n\)” style="alinhamento vertical: médio; ">0,1	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_1=y_0+hf(x_0,y_0)=1.7$
\ (n\)” style="alinhamento vertical: médio; ">2	\ (x_n\)” style="alinhamento vertical: médio; ">0,2	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_2=y_1+hf(x_1,y_1)=1.514$
\ (n\)” style="alinhamento vertical: médio; ">3	\ (x_n\)” style="alinhamento vertical: médio; ">0,3	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_3=y_2+hf(x_2,y_2)=1.3968$
\ (n\)” style="alinhamento vertical: médio; ">4	\ (x_n\)” style="alinhamento vertical: médio; ">0,4	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_4=y_3+hf(x_3,y_3)=1.3287$
\ (n\)” style="alinhamento vertical: médio; ">5	\ (x_n\)” style="alinhamento vertical: médio; ">0,5	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_5=y_4+hf(x_4,y_4)=1.3001$
\ (n\)” style="alinhamento vertical: médio; ">6	\ (x_n\)” style="alinhamento vertical: médio; ">0,6	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_6=y_5+hf(x_5,y_5)=1.3061$
\ (n\)” style="alinhamento vertical: médio; ">7	\ (x_n\)” style="alinhamento vertical: médio; ">0,7	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_7=y_6+hf(x_6,y_6)=1.3435$
\ (n\)” style="alinhamento vertical: médio; ">8	\ (x_n\)” style="alinhamento vertical: médio; ">0,8	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_8=y_7+hf(x_7,y_7)=1.4100$
\ (n\)” style="alinhamento vertical: médio; ">9	\ (x_n\)” style="alinhamento vertical: médio; ">0,9	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_9=y_8+hf(x_8,y_8)=1.5032$
\ (n\)” style="alinhamento vertical: médio; ">10	\ (x_n\)” style="alinhamento vertical: médio; ">1,0	\ (y_n=y_ {n−1} +hf (x_ {n−1}, y_ {n−1})\)” style="alinhamento vertical:meio; ">$ y_{10}=y_9+hf(x_9,y_9)=1.6202$

Com dez cálculos, podemos aproximar os valores da solução ao problema do valor inicial para valores$ x$ entre$ 0$$ 1$ e.

Acesse este site para ter a chance de explorar visualmente o método de Euler.

Exercício$\PageIndex{3}$

Considere o problema do valor inicial

\[ y′=x^3+y^2,\; y(1)=−2.\nonumber \]

Usando um tamanho de etapa de$ 0.1$, gere uma tabela com valores aproximados para a solução do problema do valor inicial para valores$ x$ entre$ 1$$ 2$ e.

Dica: Comece identificando o valor de e$ h$, em seguida, descubra o que$ f(x,y)$ é. Em seguida, use a fórmula do Método de Euler para calcular$ y_1,y_2,$ e assim por diante.

Resposta

Tabela$ \PageIndex{3}$: Usando o Método de Euler para aproximar soluções para a equação diferencial no Exercício$\PageIndex{3}$.
$ n$	\ (x_n)	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
0	1	−2
1	1.1	$ y_1=y_0+hf(x_0,y_0)=−1.5$
2	1.2	$ y_2=y_1+hf(x_1,y_1)=−1.1419$
3	1.3	$ y_3=y_2+hf(x_2,y_2)=−0.8387$
4	1.4	$ y_4=y_3+hf(x_3,y_3)=−0.5487$
5	1,5	$ y_5=y_4+hf(x_4,y_4)=−0.2442$
6	1.6	$ y_6=y_5+hf(x_5,y_5)=0.0993$
7	1.7	$ y_7=y_6+hf(x_6,y_6)=0.5099$
8	1.8	$ y_8=y_7+hf(x_7,y_7)=1.0272$
9	1.9	$ y_9=y_8+hf(x_8,y_8)=1.7159$
10	2	$ y_{10}=y_9+hf(x_9,y_9)=2.6962$

Conceitos chave

Um campo de direção é um objeto matemático usado para representar graficamente soluções para uma equação diferencial de primeira ordem.
O Método de Euler é uma técnica numérica que pode ser usada para aproximar soluções para uma equação diferencial.

Equações chave

Método de Euler

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$, onde$ h$ está o tamanho do passo

Glossário

solução assintoticamente semi-estável: $ y=k$se não for assintoticamente estável nem assintoticamente instável

solução assintoticamente estável: $ y=k$se existe$ ε>0$ tal forma que, para qualquer valor,$ c∈(k−ε,\, k+ε)$ a solução para o problema do valor inicial$ y′=f(x,y),\; y(x_0)=c$ se$ k$$ x$ aproxima do infinito

solução assintoticamente instável: $ y=k$se existe$ ε>0$ tal forma que, para qualquer valor,$ c∈(k−ε,\, k+ε)$ a solução para o problema do valor inicial$ y′=f(x,y),\; y(x_0)=c$ nunca se aproxime$ k$ quando$ x$ se aproxima do infinito

campo de direção (campo de inclinação): um objeto matemático usado para representar graficamente soluções para uma equação diferencial de primeira ordem; em cada ponto em um campo de direção, aparece um segmento de linha cuja inclinação é igual à inclinação de uma solução para a equação diferencial que passa por esse ponto

solução de equilíbrio: qualquer solução para a equação diferencial da forma$ y=c,$ onde$ c$ é uma constante

Método de Euler: uma técnica numérica usada para aproximar soluções para um problema de valor inicial

curva de solução: uma curva representada graficamente em um campo de direção que corresponde à solução para o problema do valor inicial passando por um determinado ponto no campo de direção

tamanho da etapa: o incremento hh que é adicionado ao valor xx em cada etapa do Método de Euler

Contribuidores e atribuições

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) edited this section to adjust the explanation of equilibrium points in the example shown in Figures $ \PageIndex{4}$ - $ \PageIndex{6}$. He also created these figures.

Definição: Campo de direção (campo de inclinação)

Exercício\(\PageIndex{1}\)

Definição: E quilibrium Solutions

Definição: soluções assintoticamente estáveis, instáveis e semi-estáveis

Exemplo\( \PageIndex{1}\): Stability of an Equilibrium Solution

Exercício\(\PageIndex{2}\)

Método de Euler

Exemplo\( \PageIndex{2}\): Using Euler’s Method

Exercício\(\PageIndex{3}\)

\( n\)	0	1	2	3	4	5
\( x_n\)	−1	−0,9	−0,8	−0,7	−0,6	−0,5
\( y_n\)	2	1.7	1.492	1.334	1.2046	1,0955
\( n\)	6	7	8	9	10
\( x_n\)	−0,4	−0,3	−0,2	−0,1	0
\( y_n\)	1.0004	1.9164	1.8414	1.746	1.7156

\( n\)	\ (x_n)	\( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\)
0	1	−2
1	1.1	\( y_1=y_0+hf(x_0,y_0)=−1.5\)
2	1.2	\( y_2=y_1+hf(x_1,y_1)=−1.1419\)
3	1.3	\( y_3=y_2+hf(x_2,y_2)=−0.8387\)
4	1.4	\( y_4=y_3+hf(x_3,y_3)=−0.5487\)
5	1,5	\( y_5=y_4+hf(x_4,y_4)=−0.2442\)
6	1.6	\( y_6=y_5+hf(x_5,y_5)=0.0993\)
7	1.7	\( y_7=y_6+hf(x_6,y_6)=0.5099\)
8	1.8	\( y_8=y_7+hf(x_7,y_7)=1.0272\)
9	1.9	\( y_9=y_8+hf(x_8,y_8)=1.7159\)
10	2	\( y_{10}=y_9+hf(x_9,y_9)=2.6962\)