8.5: Equações lineares de primeira ordem

Objetivos de

• Escreva uma equação diferencial linear de primeira ordem na forma padrão.
• Encontre um fator de integração e use-o para resolver uma equação diferencial linear de primeira ordem.
• Resolva problemas aplicados envolvendo equações diferenciais lineares de primeira ordem.

Anteriormente, estudamos a aplicação de uma equação diferencial de primeira ordem que envolvia a resolução da velocidade de um objeto. Em particular, se uma bola é lançada para cima com uma velocidade inicial de\( v_0\) ft/s, então um problema de valor inicial que descreve a velocidade da bola após\( t\) segundos é dado por

\[ \dfrac{dv}{dt}=−32 \nonumber \]

com\(v(0)=v_0.\)

Este modelo pressupõe que a única força que atua na bola é a gravidade. Agora, aumentamos o problema ao permitir a possibilidade de a resistência do ar atuar na bola.

A resistência do ar sempre atua na direção oposta ao movimento. Portanto, se um objeto estiver subindo, a resistência do ar age em uma direção descendente. Se o objeto estiver caindo, a resistência do ar atua em uma direção ascendente (Figura\( \PageIndex{1}\)). Não existe uma relação exata entre a velocidade de um objeto e a resistência do ar que atua sobre ele. Para objetos muito pequenos, a resistência do ar é proporcional à velocidade; ou seja, a força devida à resistência do ar é numericamente igual a alguns\( k\) tempos constantes\( v\). Para objetos maiores (por exemplo, do tamanho de uma bola de beisebol), dependendo da forma, a resistência do ar pode ser aproximadamente proporcional ao quadrado da velocidade. De fato, a resistência do ar pode ser proporcional a\( v^{1.5}\)\( v^{0.9}\), ou alguma outra potência de\( v\).

Figura\( \PageIndex{1}\): Forças atuando em uma bola de beisebol em movimento: a gravidade age na direção descendente e a resistência do ar atua em uma direção oposta à direção do movimento.

Trabalharemos com a aproximação linear da resistência do ar. Se assumirmos\( k>0\), a expressão da força\( F_A\) devida à resistência do ar é dada por\( FA_=−kv\). Portanto, a soma das forças que atuam sobre o objeto é igual à soma da força gravitacional e da força devida à resistência do ar. Isso, por sua vez, é igual à massa do objeto multiplicada por sua aceleração no tempo\( t\) (segunda lei de Newton). Isso nos dá a equação diferencial

\[ m\dfrac{dv}{dt}=−kv−mg. \nonumber \]

Finalmente, impomos uma condição inicial\( v(0)=v_0,\) onde\( v_0\) é a velocidade inicial medida em metros por segundo. Isso faz com que\( g=9.8m/s^2.\) o problema do valor inicial se torne

\[ m\dfrac{dv}{dt}=−kv−mg \nonumber \]

com\(v(0)=v_0.\)

A equação diferencial neste problema de valor inicial é um exemplo de uma equação diferencial linear de primeira ordem. (Lembre-se de que uma equação diferencial é de primeira ordem se a derivada de maior ordem que aparece na equação for\( 1\).) Nesta seção, estudamos equações lineares de primeira ordem e examinamos um método para encontrar uma solução geral para esses tipos de equações, bem como resolver problemas de valor inicial envolvendo elas.

Definição: Equação diferencial linear de primeira ordem

Uma equação diferencial de primeira ordem é linear se puder ser escrita na forma

\[a(x)y′+b(x)y=c(x), \nonumber \]

onde\( a(x),b(x),\) e\( c(x)\) são funções arbitrárias de\( x\).

Lembre-se de que a função desconhecida\( y\) depende da variável\( x\); ou seja,\( x\) é a variável independente e\( y\) é a variável dependente. Alguns exemplos de equações diferenciais lineares de primeira ordem são

\[ (3x^2−4)y'+(x−3)y=\sin x \nonumber \]

\[ (\sin x)y'−(\cos x)y=\cot x \nonumber \]

\[ 4xy'+(3\ln x)y=x^3−4x. \nonumber \]

Exemplos de equações diferenciais não lineares de primeira ordem incluem

\[ (y')^4−(y')^3=(3x−2)(y+4) \nonumber \]

\[ 4y'+3y^3=4x−5 \nonumber \]

\[(y')^2=\sin y+\cos x. \nonumber \]

Essas equações não são lineares por causa de termos como\( (y′)^4,y^3,\) etc. Devido a esses termos, é impossível colocar essas equações na mesma forma que Equação.

Formulário padrão

Considere a equação diferencial

\[ (3x^2−4)y′+(x−3)y=\sin x. \nonumber \]

Nosso principal objetivo nesta seção é derivar um método de solução para equações dessa forma. É útil ter o coeficiente de\( y′\) ser igual\( 1\) a. Para que isso aconteça, dividimos os dois lados por\( 3x^2−4.\)

\[ y′+ \left(\dfrac{x−3}{3x^2−4} \right)y=\dfrac{\sin x}{3x^2−4} \nonumber \]

Isso é chamado de forma padrão da equação diferencial. Nós o usaremos mais tarde ao encontrar a solução para uma equação diferencial linear geral de primeira ordem. Voltando à Equação, podemos dividir os dois lados da equação por\( a(x)\). Isso leva à equação

\[ y′+\dfrac{b(x)}{a(x)}y=\dfrac{c(x)}{a(x)}. \label{eq5} \]

Agora defina

\[ p(x)=\dfrac{b(x)}{a(x)} \nonumber \]

e

\[ q(x)=\dfrac{c(x)}{a(x)} \nonumber \]

Então a Equação\ ref {eq5} se torna

\[ y′+p(x)y=q(x). \nonumber \]

Podemos escrever qualquer equação diferencial linear de primeira ordem nesse formato, e isso é conhecido como a forma padrão para uma equação diferencial linear de primeira ordem.

Exemplo\( \PageIndex{1}\): Writing First-Order Linear Equations in Standard Form

Coloque cada uma das seguintes equações diferenciais lineares de primeira ordem na forma padrão. Identifique\( p(x)\) e\( q(x)\) para cada equação.

1. \( y'=3x−4y\)
2. \( \dfrac{3xy'}{4y−3}=2\)(aqui\( x>0\))
3. \( y=3y'−4x^2+5\)

Solução

a. Adicione\( 4y\) aos dois lados:

\( y'+4y=3x.\)

Nesta equação,\( p(x)=4\) e\ | (q (x) =3x.\)

b. Multiplique os dois lados por e\( 4y−3\), em seguida, subtraia\( 8y\) de cada lado:

\( \dfrac{3xy'}{4y−3}=2\)

\( 3xy'=2(4y−3)\)

\( 3xy'=8y−6\)

\( 3xy'−8y=−6.\)

Finalmente, divida os dois lados por\( 3x\) para tornar o coeficiente\( y'\) igual a\( 1\):

\( y'−\dfrac{8}{3x}y=−\dfrac{2}{3x}.\)

Isso é permitido porque, na declaração original desse problema, presumimos que\( x>0\). (Se\( x=0\) então a equação original se tornar\( 0=2\), o que é claramente uma afirmação falsa.)

Nesta equação,\( p(x)=−\dfrac{8}{3x}\)\( q(x)=−\dfrac{2}{3x}\) e.

c. Subtraia\( y\) de cada lado e adicione\( 4x^2−5\):

\( 3y'−y=4x^2−5.\)

Em seguida, divida os dois lados por\( 3\):

\( y'−\dfrac{1}{3}y=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Nesta equação,\( p(x)=−\dfrac{1}{3}\)\( q(x)=\dfrac{4}{3}x^2−\dfrac{5}{3}\) e.

Exercício\(\PageIndex{1}\)

Coloque a equação\( \dfrac{(x+3)y'}{2x−3y−4}=5\) na forma padrão\( p(x)\) e identifique\( q(x)\) e.

Dica

Multiplique os dois lados pelo denominador comum e, em seguida, colete todos os termos envolvidos\( y\) em um lado.

Responda

\[ y'+\dfrac{15}{x+3}y=\dfrac{10x−20}{x+3} \nonumber \]

\[p(x)=\dfrac{15}{x+3} \nonumber \]

e

\[ q(x)=\dfrac{10x−20}{x+3} \nonumber \]

Fatores integradores

Agora desenvolvemos uma técnica de solução para qualquer equação diferencial linear de primeira ordem. Começamos com a forma padrão de uma equação diferencial linear de primeira ordem:

\[ y'+p(x)y=q(x). \label{Deq1} \]

O primeiro termo no lado esquerdo da Equação é a derivada da função desconhecida, e o segundo termo é o produto de uma função conhecida com a função desconhecida. Isso lembra um pouco a regra do poder. Se multiplicarmos a Equação\ ref {Deq1} por uma função ainda a ser determinada\( μ(x)\), a equação se torna

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq2} \]

A equação do lado esquerdo\ ref {Deq2} pode ser perfeitamente compatível com a regra do produto:

\[ \dfrac{d}{dx}[f(x)g(x)]=f′(x)g(x)+f(x)g′(x). \nonumber \]

A correspondência termo por termo dá\( y=f(x),g(x)=μ(x)\),\( g′(x)=μ(x)p(x)\) e. Pegar a derivada de\( g(x)=μ(x)\) e defini-la igual ao lado direito de\( g′(x)=μ(x)p(x)\) leva a

\[ μ′(x)=μ(x)p(x). \nonumber \]

Esta é uma equação diferencial separável de primeira ordem para\(μ(x).\) Nós sabemos\( p(x)\) porque ela aparece na equação diferencial que estamos resolvendo. Separação de variáveis e integração de rendimentos

\[ \begin{align} \dfrac{μ′(x)}{μ(x)} =p(x) \\[4pt] ∫\dfrac{μ′(x)}{μ(x)}dx =∫p(x)dx \\[4pt] \ln|μ(x)| =∫p(x)dx+C \\[4pt] e^{\ln|μ(x)|} =e^{∫p(x)dx+C} \\[4pt] |μ(x)| =C_1e^{∫p(x)dx} \\[4pt] μ(x) =C_2e^{∫p(x)dx}. \end{align} \nonumber \]

Aqui\( C_2\) pode ser uma constante arbitrária (positiva ou negativa). Isso leva a um método geral para resolver uma equação diferencial linear de primeira ordem. Primeiro multiplicamos os dois lados da equação pelo fator de integração.\( μ(x).\) Isso dá

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq5} \]

O lado esquerdo da Equação\ ref {Deq5} pode ser reescrito como\( \dfrac{d}{dx}(μ(x)y)\).

\[ \dfrac{d}{dx}(μ(x)y)=μ(x)q(x). \label{Deq6} \]

Em seguida, integre os dois lados da Equação\ ref {Deq6} em relação\(x\) a.

\[ \begin{align} ∫\dfrac{d}{dx}(μ(x)y)dx =∫μ(x)q(x)dx \\[4pt] μ(x)y =∫μ(x)q(x)dx \label{Deq7} \end{align} \]

Divida os dois lados da Equação\ ref {Deq6} por\( μ(x)\):

\[ y=\dfrac{1}{μ(x)}\left[∫μ(x)q(x)dx+C\right]. \nonumber \]

Como\( μ(x)\) foi calculado anteriormente, agora terminamos. Uma observação importante sobre a constante de integração\( C\): pode parecer que somos inconsistentes no uso da constante integradora. No entanto, o envolvimento integral\( p(x)\) é necessário para encontrar um fator integrador para a Equação. Somente um fator de integração é necessário para resolver a equação; portanto, é seguro atribuir um valor\(C\) para essa integral. Nós escolhemos\(C=0\). Ao calcular a integral dentro dos colchetes na Equação, é necessário manter nossas opções abertas para o valor da constante integradora, porque nosso objetivo é encontrar uma família geral de soluções para a Equação. Esse fator integrador garante exatamente isso.

Estratégia de resolução de problemas: Resolvendo uma equação diferencial linear de primeira ordem

1. Coloque a equação na forma padrão\( p(x)\) e identifique\( q(x)\) e.
2. Calcule o fator de integração\[ μ(x)=e^{∫p(x)dx}. \nonumber \]
3. Multiplique os dois lados da equação diferencial por\( μ(x)\).
4. Integre os dois lados da equação obtida na etapa\( 3\) e divida os dois lados por\( μ(x)\).
5. Se houver uma condição inicial, determine o valor de\( C\).

Exemplo\( \PageIndex{2}\): Solving a First-order Linear Equation

Encontre uma solução geral para a equação diferencial\( xy'+3y=4x^2−3x.\) Assuma\( x>0.\)

Solução

1. Para colocar essa equação diferencial na forma padrão, divida os dois lados por\( x\):

\[ y'+\dfrac{3}{x}y=4x−3. \nonumber \]

Portanto,\( p(x)=\dfrac{3}{x}\) e\( q(x)=4x−3.\)

2. O fator integrador é\( μ(x)=e^{∫(3/x)}dx=e^{3 \ln x}=x^3\).

3. Multiplicar os dois lados da equação diferencial por nos\( μ(x)\) dá

\[ \begin{align*} x^3y′+x^3(\dfrac{3}{x}) =x^3(4x−3) \\[4pt] x^3y′+3x^2y =4x^4−3x^3 \\[4pt] \dfrac{d}{dx}(x^3y) = 4x^4−3x^3. \end{align*}\]

4. Integre os dois lados da equação.

\[ \begin{align*} ∫\dfrac{d}{dx}(x^3y)dx = ∫4x^4−3x^3dx \\[4pt] x^3y =\dfrac{4x^5}{5}−\dfrac{3x^4}{4}+C \\[4pt] y =\dfrac{4x^2}{5}−\dfrac{3x}{4}+Cx^{−3}. \end{align*}\]

5. Não há valor inicial, então o problema está completo.

Análise

Você deve ter notado a condição que foi imposta à equação diferencial; a saber,\( x>0\). Para qualquer valor diferente de zero de\( C\), a solução geral não está definida em\( x=0\). Além disso, quando\( x<0\), o fator integrador muda. O fator de integração é dado pela Equação como\( f(x)=e^{∫p(x)dx}\). Para isso,\( p(x)\) obtemos

\[ \begin{align*} e^{∫p(x)dx} =e^{∫(3/x)dx} \\[4pt] =e^{3\ln|x|} \\[4pt] =|x|^3 \end{align*}\]

desde\(x<0\). O comportamento da solução geral muda em\( x=0\) grande parte devido ao fato de\( p(x)\) não estar definido lá.

Exercício\(\PageIndex{2}\)

Encontre a solução geral para a equação diferencial\( (x−2)y'+y=3x^2+2x.\) Assume\( x>2\).

Dica

Use o método descrito na estratégia de resolução de problemas para equações diferenciais lineares de primeira ordem.

Responda

\( y=\dfrac{x^3+x^2+C}{x−2}\)

Agora usamos a mesma estratégia para encontrar a solução para um problema de valor inicial.

Exemplo\( \PageIndex{3}\): A First-order Linear Initial-Value Problem

Resolva o problema do valor inicial

\[ y′+3y=2x−1,y(0)=3. \nonumber \]

Solução

1. Essa equação diferencial já está na forma padrão com\( p(x)=3\)\( q(x)=2x−1\) e.

2. O fator integrador é\( μ(x)=e^{∫3dx}=e^{3x}\).

3. Multiplicando os dois lados da equação diferencial por\( μ(x)\) dá

\[ \begin{align*} e^{3x}y′+3e^{3x}y =(2x−1)e^{3x} \\[4pt] \dfrac{d}{dx}[ye^{3x}] =(2x−1)e^{3x}. \end{align*}\]

Integre os dois lados da equação:

\( ∫\dfrac{d}{dx}[ye^{3x}]dx=∫(2x−1)e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}}{3}(2x−1)−∫\dfrac{2}{3}e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}(2x−1)}{3}−\dfrac{2e^{3x}}{9}+C\)

\( y=\dfrac{2x−1}{3}−\dfrac{2}{9}+Ce^{−3x}\)

\( y=\dfrac{2x}{3}−\dfrac{5}{9}+Ce^{−3x}\).

4. Agora substitua\( x=0\) e\( y=3\) entre na solução geral e resolva por\( C\):

\[ \begin{align*} y =\dfrac{2}{3}x−\dfrac{5}{9}+Ce^{−3x} \\[4pt] 3 =\dfrac{2}{3}(0)−\dfrac{5}{9}+Ce^{−3(0)} \\[4pt] 3 =−\dfrac{5}{9}+C \\[4pt] C=\dfrac{32}{9}. \end{align*}\]

Portanto, a solução para o problema do valor inicial é

\[ y=\dfrac{2}{3}x−\dfrac{5}{9}+\dfrac{32}{9}e^{−3x}. \nonumber \]

Exemplo\(\PageIndex{4}\):

Resolva o problema do valor inicial\[ y'−2y=4x+3y(0)=−2. \nonumber \]

Solução

\[ y=−2x−4+2e^{2x} \nonumber \]

Aplicações de equações diferenciais lineares de primeira ordem

Examinamos duas aplicações diferentes de equações diferenciais lineares de primeira ordem. O primeiro envolve a resistência do ar no que se refere a objetos que estão subindo ou descendo; o segundo envolve um circuito elétrico. Outras aplicações são numerosas, mas a maioria é resolvida de forma semelhante.

Queda livre com resistência ao ar

Discutimos a resistência do ar no início desta seção. O próximo exemplo mostra como aplicar esse conceito para uma bola em movimento vertical. Outros fatores podem afetar a força da resistência do ar, como o tamanho e a forma do objeto, mas nós os ignoramos aqui.

Exemplo\( \PageIndex{5}\): A Ball with Air Resistance

Uma bola de raquetebol é atingida diretamente para cima com uma velocidade inicial de\( 2\) m/s. A massa de uma bola de raquetebol é de aproximadamente\( 0.0427\) kg. A resistência do ar atua na bola com uma força numericamente igual a\( 0.5v\), onde\( v\) representa a velocidade da bola no momento\( t\).

1. Determine a velocidade da bola em função do tempo.
2. Quanto tempo a bola leva para atingir sua altura máxima?
3. Se a bola for atingida a partir de uma altura inicial de um\( 1\) metro, qual será a altura que ela alcançará?

Solução

a. A massa\( m=0.0427kg,k=0.5,\)\( g=9.8m/s^2\) e. A velocidade inicial é\( v_0=2 m/s\). Portanto, o problema do valor inicial é

\( 0.0427\dfrac{dv}{dt}=−0.5v−0.0427(9.8),v_0=2.\)

Dividindo a equação diferencial por\( 0.0427\) dá

\( \dfrac{dv}{dt}=−11.7096v−9.8,v_0=2.\)

A equação diferencial é linear. Usando a estratégia de resolução de problemas para equações diferenciais lineares:

Etapa 1. Reescreva a equação diferencial como\( \dfrac{dv}{dt}+11.7096v=−9.8\). Isso dá\( p(t)=11.7096\) e\( q(t)=−9.8\)

Etapa 2. O fator integrador é\( μ(t)=e^{∫11.7096dt}=e^{11.7096t}.\)

Etapa 3. Multiplique a equação diferencial por\( μ(t)\):

\( e^{11.7096t\dfrac{dv}{dt}}+11.7096ve^{11.7096t}=−9.8e^{11.7096t}\)

\( \dfrac{d}{dt}[ve^{11.7096t}]=−9.8e^{11.7096t}.\)

Etapa 4. Integre os dois lados:

\( ∫\dfrac{d}{dt}[ve^{11.7096t}]dt=∫−9.8e^{11.7096t}dt\)

\( ve^{11.7096t}=\dfrac{−9.8}{11.7096}e^{11.7096t}+C\)

\( v(t)=−0.8369+Ce^{−11.7096t}.\)

Etapa 5. Resolva o\( C\) uso da condição inicial\( v_0=v(0)=2\):

\( v(t)=−0.8369+Ce^{−11.7096t}\)

\( v(0)=−0.8369+Ce^{−11.7096(0)}\)

\( 2=−0.8369+C\)

\( C=2.8369.\)

Portanto, a solução para o problema do valor inicial é

\( v(t)=2.8369e^{−11.7096t}−0.8369.\)

b. A bola atinge sua altura máxima quando a velocidade é igual a zero. A razão é que quando a velocidade é positiva, ela está aumentando e, quando é negativa, está caindo. Portanto, quando é zero, não está subindo nem descendo e está em sua altura máxima:

\( 2.8369e^{−11.7096t}−0.8369=0\)

\( 2.8369e^{−11.7096t}=0.8369\)

\( e^{−11.7096t}=\dfrac{0.8369}{2.8369}≈0.295\)

\( lne^{−11.7096t}=ln0.295≈−1.221\)

\( −11.7096t=−1.221\)

\( t≈0.104.\)

Portanto, leva aproximadamente um\( 0.104\) segundo para atingir a altura máxima.

c. Para determinar a altura da bola em função do tempo, use o fato de que a derivada da posição é a velocidade, ou seja, se\( h(t)\) representa a altura no momento\( t\), então\( h′(t)=v(t)\). Como sabemos\( v(t)\) a altura inicial, podemos formar um problema de valor inicial:

\( h′(t)=2.8369e^{−11.7096t}−0.8369,h(0)=1.\)

Integrando os dois lados da equação diferencial em relação a\( t\) dá

\( ∫h′(t)dt=∫2.8369e^{−11.7096t}−0.8369dt\)

\( h(t)=−\dfrac{2.8369}{11.7096}e^{−11.7096t}−0.8369t+C\)

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C.\)

Resolva para\( C\) usando a condição inicial:

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C\)

\( h(0)=−0.2423e^{−11.7096(0)}−0.8369(0)+C\)

\( 1=−0.2423+C\)

\( C=1.2423.\)

Portanto

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+1.2423.\)

Após o\( 0.104\) segundo, a altura é dada por

\( h(0.2)=−0.2423e^{−11.7096t}−0.8369t+1.2423≈1.0836\)contador.

Exercício\(\PageIndex{3}\)

O peso de um centavo é de\(2.5\) gramas (United States Mint, “Coin Specifications”, acessado em 9 de abril de 2015, http://www.usmint.gov/about_the_mint...specifications), e o mirante superior do Empire State Building fica\( 369\) metros acima da rua. Como o centavo é um objeto pequeno e relativamente liso, a resistência do ar que atua sobre o centavo é, na verdade, muito pequena. Assumimos que a resistência do ar é numericamente igual\( 0.0025v\) a. Além disso, o centavo é descartado sem que nenhuma velocidade inicial seja atribuída a ele.

1. Configure um problema de valor inicial que represente a queda do centavo.
2. Resolva o problema do\( v(t)\).
3. Qual é a velocidade terminal do centavo (ou seja, calcule o limite da velocidade quando\( t\) se aproxima do infinito)?

Dica

Configure a equação diferencial da mesma forma que Example. Lembre-se de converter de gramas em quilogramas.

Responda

uma.\( \dfrac{dv}{dt}=−v−9.8\)\( v(0)=0\)

b.\( v(t)=9.8(e^{−t}−1)\)

c.\( \lim_{t→∞}v(t)=\lim_{t→∞}(9.8(e^{−t}−1))=−9.8m/s≈−21.922mph\)

Circuitos elétricos

Uma fonte de força eletromotriz (por exemplo, uma bateria ou gerador) produz um fluxo de corrente em um circuito fechado, e essa corrente produz uma queda de tensão em cada resistor, indutor e capacitor no circuito. A Regra de Circuito de Kirchhoff afirma que a soma das quedas de tensão entre resistores, indutores e capacitores é igual à força eletromotriz total em um circuito fechado. Temos os três resultados a seguir:

1. A queda de tensão em um resistor é dada por

\( E_R=Ri,\)

onde\( R\) está uma constante de proporcionalidade chamada resistência e\( i\) é a corrente.

2. A queda de tensão em um indutor é dada por

\( EL=Li′\),

onde\( L\) é uma constante de proporcionalidade chamada indutância, e\( i\) novamente denota a corrente.

3. A queda de tensão em um capacitor é dada por

\( E_C=\dfrac{1}{C}q\),

onde\( C\) está uma constante de proporcionalidade chamada capacitância e\( q\) é a carga instantânea no capacitor. A relação entre\( i\) e\( q\) é\( i=q′\).

Usamos unidades de volts\( (V)\) para medir a tensão\( E\), amperes\( (A)\) para medir a corrente\( i\), coulombs\( (C)\) para medir a carga\( q\), ohms\( (Ω)\) para medir a resistência\( R\), henrys\( (H)\) para medir a indutância\( L\) e farads\( (F)\) para medir capacitância\( C\). Considere o circuito na Figura\( \PageIndex{2}\).

Figura\( \PageIndex{2}\): Um circuito elétrico típico, contendo um gerador de tensão\( (V_S)\), capacitor\( (C)\), indutor\( (L)\) e resistor\( (R)\).

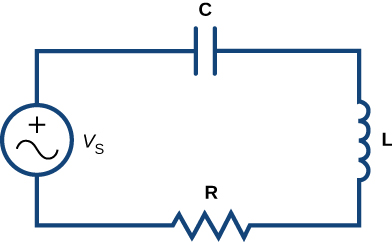
Aplicando a Regra de Circuito de Kirchhoff a este circuito, deixamos\( E\) indicar a força eletromotriz fornecida pelo gerador de tensão. Então

\( E_L+E_R+E_C=E\).

Substituindo as expressões por\( E_L,E_R,\) e\( E_C\) nesta equação, obtemos

\( Li′+Ri+\dfrac{1}{C}q=E.\)

Se não houver capacitor no circuito, a equação se torna

\( Li′+R_i=E.\)

Esta é uma equação diferencial de primeira ordem em\( i\). O circuito é chamado de\( LR\) circuito.

Em seguida, suponha que não haja indutor no circuito, mas haja um capacitor e um resistor,\( C≠0.\) então\( L=0,R≠0,\) a equação pode ser reescrita como

\( Rq′+\dfrac{1}{C}q=E,\)

que é uma equação diferencial linear de primeira ordem. Isso é conhecido como um circuito RC. Em ambos os casos, podemos configurar e resolver um problema de valor inicial.

Circuito elétrico

Um circuito tem em série uma força eletromotriz dada por\( E=50\sin 20tV,\) um resistor de\( 5Ω\), e um indutor de\( 0.4H\). Se a corrente inicial for\( 0\), encontre a corrente no momento\( t>0\).

Solução

Temos um resistor e um indutor no circuito, então usamos a Equação. A queda de tensão no resistor é dada por\( E_R=R_i=5_i\). A queda de tensão no indutor é dada por\( E_L=Li′=0.4i′\). A força eletromotriz se torna o lado direito da Equação. Portanto, a equação se torna

\[ 0.4i′+5i=50\sin 20t. \nonumber \]

Dividindo os dois lados por\( 0.4\) dá a equação

\[ i′+12.5i=125\sin 20t. \nonumber \]

Como a corrente inicial é 0, esse resultado fornece uma condição inicial de\( i(0)=0.\) Podemos resolver esse problema de valor inicial usando a estratégia de cinco etapas para resolver equações diferenciais de primeira ordem.

Etapa 1. Reescreva a equação diferencial como\( i′+12.5i=125\sin 20t\). Isso dá\( p(t)=12.5\)\( q(t)=125\sin 20t\) e.

Etapa 2. O fator integrador é\( μ(t)=e^{∫12.5dt}=e^{12.5t}\).

Etapa 3. Multiplique a equação diferencial por\( μ(t)\):

\( e^{12.5t}i′+12.5e^{12.5t}i=125e^{12.5t}\sin 20t\)

\( \dfrac{d}{dt}[ie^{12.5}t]=125e^{12.5t}\sin 20t\).

Etapa 4. Integre os dois lados:

\( ∫\dfrac{d}{dt}[ie^{12.5t}]dt=∫125e^{12.5t}\sin 20tdt\)

\( ie^{12.5t}=(\dfrac{250\sin 20t−400\cos 20t}{89})e^{12.5t}+C\)

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\).

Etapa 5. Resolva o\( C\) uso da condição inicial\( v(0)=2\):

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\)

\( i(0)=\dfrac{250sin20(0)−400cos20(0)}{89}+Ce^{−12.5(0)}\)

\( 0=−\dfrac{400}{89}+C\)

\( C=\dfrac{400}{89}\).

Portanto, a solução para o problema do valor inicial é

\[ i(t)=\dfrac{250\sin 20t−400\cos 20t+400e^{−12.5t}}{89}=\dfrac{250\sin 20t−400\cos 20t}{89}+\dfrac{400e^{−12.5t}}{89}. \nonumber \]

O primeiro termo pode ser reescrito como uma única função de cosseno. Primeiro, multiplique e divida por\( \sqrt{250^2+400^2}=50\sqrt{89}\):

\( \dfrac{250\sin 20t−400\cos 20t}{89}=\dfrac{50\sqrt{89}}{89}(\dfrac{250\sin 20t−400\cos 20t}{50\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})\).

Em seguida,\( φ\) defina como um ângulo agudo tal que\( \cos φ=\dfrac{8}{\sqrt{89}}\). Em seguida,\( \sin φ=\dfrac{5}{\sqrt{89}}\) e

\( −\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\cos φ\cos 20t−\sin φ\sin 20t)=−\dfrac{50\sqrt{89}}{89}\cos(20t+φ).\)

Portanto, a solução pode ser escrita como

\( i(t)=−\dfrac{50\sqrt{89}}{89}cos(20t+φ)+\dfrac{400e^{−12.5t}}{89}\).

O segundo termo é chamado de termo de atenuação, porque desaparece rapidamente\( t\) à medida que cresce. A mudança de fase é dada por\( φ\), e a amplitude da corrente de estado estacionário é dada por\( \dfrac{50\sqrt{89}}{89}\). O gráfico dessa solução aparece na Figura\( \PageIndex{3}\):

Figura\( \PageIndex{3}\).

Exercício\(\PageIndex{4}\)

Um circuito tem em série uma força eletromotriz dada por\( E=20sin5t\) V, um capacitor com capacitância\( 0.02F\) e um resistor de\( 8Ω\). Se a cobrança inicial for\( 4C\), encontre a cobrança no momento\( t>0\).

Dica

Use a Equação para um\( RC\) circuito para configurar um problema de valor inicial.

Responda

Problema de valor inicial:

\( 8q′+\dfrac{1}{0.02}q=20sin5t,q(0)=4\)

\( q(t)=\dfrac{10sin5t−8cos5t+172e^{−6.25t}}{41}\)

Conceitos-chave

• Qualquer equação diferencial linear de primeira ordem pode ser escrita no formulário\( y'+p(x)y=q(x)\).
• Podemos usar uma estratégia de resolução de problemas em cinco etapas para resolver uma equação diferencial linear de primeira ordem que pode ou não incluir um valor inicial.
• As aplicações de equações diferenciais lineares de primeira ordem incluem determinar o movimento de um objeto ascendente ou descendente com resistência ao ar e encontrar corrente em um circuito elétrico.

Equações-chave

• formulário padrão

\( y'+p(x)y=q(x)\)

• fator integrador

\( μ(x)=e^{∫p(x)dx}\)

Glossário

fator integrador

qualquer função\(f(x)\) que seja multiplicada em ambos os lados de uma equação diferencial para tornar o lado que envolve a função desconhecida igual à derivada de um produto de duas funções

linear

descrição de uma equação diferencial de primeira ordem que pode ser escrita na forma\( a(x)y′+b(x)y=c(x)\)

formulário padrão

a forma de uma equação diferencial linear de primeira ordem obtida escrevendo a equação diferencial na forma\( y'+p(x)y=q(x)\)