6.2E: Exercícios para a Seção 6.2

Last updated
Save as PDF

Page ID: 187848

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Derive a fórmula para o volume de uma esfera usando o método de fatiamento.

2) Use o método de corte para derivar a fórmula para o volume de um cone.

3) Use o método de corte para derivar a fórmula para o volume de um tetraedro com comprimento lateral$a.$

4) Use o método do disco para derivar a fórmula para o volume de um cilindro trapezoidal.

5) Explique quando você usaria o método do disco versus o método lavador. Quando eles são intercambiáveis?

Volumes por fatiamento

Para os exercícios 6 a 10, desenhe uma fatia típica e encontre o volume usando o método de corte para o volume determinado.

6) Uma pirâmide com altura de 6 unidades e base quadrada de 2 unidades laterais, conforme ilustrado aqui.

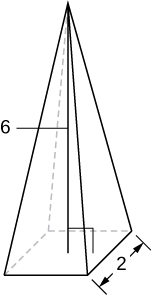
$Esta figura é uma pirâmide com largura de base de 2 e altura de 6 unidades.$

Solução:: Aqui, as seções transversais são quadrados perpendiculares$y$ ao eixo.
Usamos a seção transversal vertical da pirâmide através de seu centro para obter uma equação relacionando$x$$y$ e.
Aqui, essa seria a equação,$ y = 6 - 6x $. Como precisamos das dimensões do quadrado em cada$y$ nível, resolvemos essa equação$x$ para obter,$x = 1 - \tfrac{y}{6}$.
Esta é a metade da distância através da seção transversal quadrada no$y$ nível -, então o comprimento do lado da seção transversal quadrada é,$s = 2\left(1 - \tfrac{y}{6}\right).$
Assim, temos a área de uma seção transversal é,

$A(y) = \left[2\left(1 - \tfrac{y}{6}\right)\right]^2 = 4\left(1 - \tfrac{y}{6}\right)^2.$

\ (\ begin {align*}\ text {Então},\ quad V &=\ int_0^6 4\ left (1 -\ tfrac {y} {6}\ direita) ^2\, dy\\ [5pt]
&= -24\ int_1^0 u^2\, du,\ quad\ text {onde}\, u = 1 -\ tfrac {y} {6},\,\ text {so}\, du = -\ tfrac {1} {6}\, dy,\ quad\ implies\ quad -6\, du = dy\\ [5pt]
&= 24\ int_0^1 u^2\, du = 24\ dfrac {u^3} {3}\ bigg|_0^1\\ [5pt]
&= 8u^3\ bigg|_0^1\\ [5pt]
&= 8\ left (1^3 - 0^3\ right)\ quad=\ quad 8\,\ text {unidades} ^3\ end {align*}\)

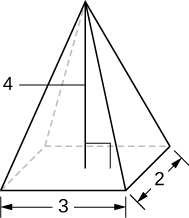
7) Uma pirâmide com altura de 4 unidades e uma base retangular com comprimento de 2 unidades e largura de 3 unidades, conforme ilustrado aqui.

$Esta figura é uma pirâmide com largura de base de 2, comprimento de 3 e altura de 4 unidades.$

8) Um tetraedro com um lado base de 4 unidades, como visto aqui.

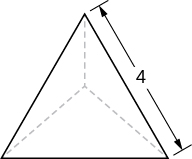
$Esta figura é um triângulo equilátero com comprimento lateral de 4 unidades.$

Resposta: $V = \frac{32}{3\sqrt{2}} = \frac{16\sqrt{2}}{3}$unidades ³

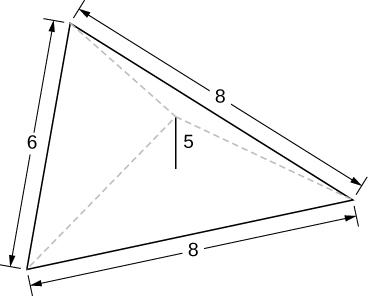
9) Uma pirâmide com altura de 5 unidades e uma base triangular isósceles com comprimentos de 6 unidades e 8 unidades, como visto aqui.

$Esta figura é uma pirâmide com base triangular. A vista é da base. Os lados do triângulo medem 6 unidades, 8 unidades e 8 unidades. A altura da pirâmide é de 5 unidades.$

10) Um cone de raio$ r$ e altura$ h$ tem um cone menor de raio$ r/2$ e altura$ h/2$ removido da parte superior, como visto aqui. O sólido resultante é chamado de frustum.

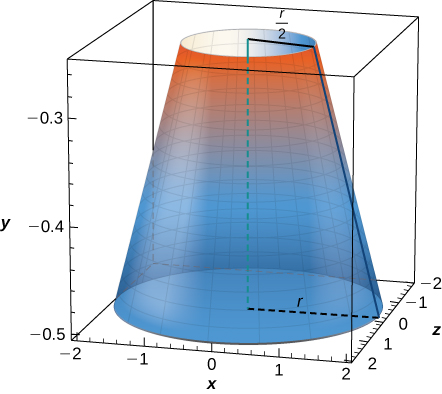
$Esta figura é um gráfico tridimensional de um cone invertido. O cone está dentro de um prisma retangular que representa o sistema de coordenadas xyz. o raio da parte inferior do cone é “r” e o raio da parte superior do cone é rotulado como “r/2”.$

Resposta: $V = \frac{7\pi}{12} hr^2$unidades ³

Para os exercícios 11 a 16, desenhe um contorno do sólido e encontre o volume usando o método de corte.

11) A base é um círculo de raio$ a$. As fatias perpendiculares à base são quadradas.

12) A base é um triângulo com vértices$ (0,0),(1,0),$$ (0,1)$ e. As fatias perpendiculares ao$xy$ plano -são semicírculos.

Resposta

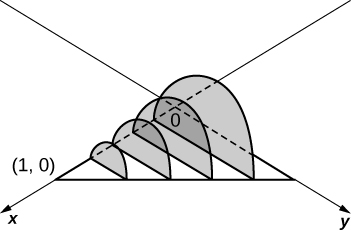
$Esta figura mostra o eixo x e o eixo y com uma linha começando no eixo x em (1,0) e terminando no eixo y em (0,1). Perpendiculares ao plano xy estão 4 semicírculos sombreados com seus diâmetros começando no eixo x e terminando na linha, diminuindo de tamanho longe da origem.$

$\displaystyle V = \int_0^1 \frac{\pi(1-x)^2}{8}\, dx \quad = \quad \frac{π}{24}$unidades ³

13) A base é a região abaixo da parábola$ y=1−x^2$ no primeiro quadrante. As fatias perpendiculares ao$xy$ plano -são quadrados.

14) A base é a região abaixo da parábola$ y=1−x^2$ e acima do $x$eixo. As fatias perpendiculares ao $y$eixo -são quadrados.

Resposta

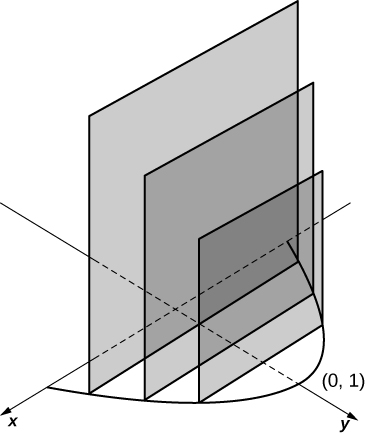
$Esta figura mostra o eixo x e o eixo y em perspectiva tridimensional. No gráfico acima do eixo x há uma parábola, que tem seu vértice em y=1 e x intercepta em (-1,0) e (1,0). Existem 3 regiões quadradas sombreadas perpendiculares ao plano x y, que tocam a parábola em ambos os lados, diminuindo de tamanho longe da origem.$

$\displaystyle V = \int_0^1 4(1 - y)\,dy \quad = \quad 2$unidades ³

15) A base é a região delimitada por$ y=x^2)$ e$ y=9.$ as fatias perpendiculares ao$x$ eixo -são triângulos isósceles retos.

16) A base é a área entre$ y=x$$ y=x^2$ e. As fatias perpendiculares ao$x$ eixo -são semicírculos.

Resposta

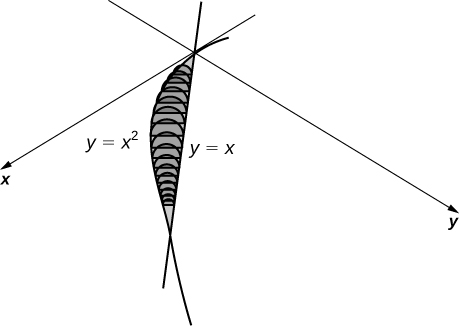
$Esta figura é um gráfico com os eixos x e y na diagonal para mostrar a perspectiva tridimensional. No primeiro quadrante do gráfico estão as curvas y=x, uma linha e y=x^2, uma parábola. Eles se cruzam na origem e em (1,1). Várias regiões sombreadas de formato semicircular são perpendiculares ao plano x y, que vão da parábola à linha e perpendiculares à linha.$

$\displaystyle V = \int_0^1 \frac{\pi}{8}\left( x - x^2 \right)^2 \, dx \quad=\quad \frac{π}{240}$unidades ³

Método de disco e lavadora

Para os exercícios 17 a 24, desenhe a região delimitada pelas curvas. Em seguida, use o método de disco ou lavadora para encontrar o volume quando a região é girada em torno do$x$ eixo.

17)$ x+y=8,\quad x=0$, e$ y=0$

18)$ y=2x^2,\quad x=0,\quad x=4,$ e$ y=0$

Resposta

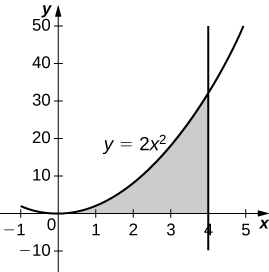
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela curva y=2x^2, abaixo pelo eixo x e à direita pela linha vertical x=4.$

$\displaystyle V = \int_0^4 4\pi x^4\, dx \quad=\quad \frac{4096π}{5}$unidades ³

19)$ y=e^x+1,\quad x=0,\quad x=1,$ e$ y=0$

20)$ y=x^4,\quad x=0$ e$ y=1$

Resposta

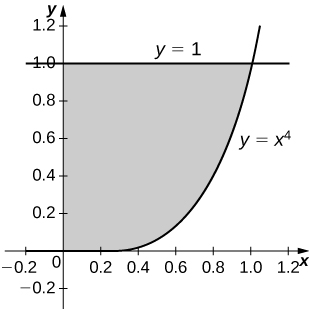
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela linha y=1, abaixo pela curva y=x^4 e à esquerda pelo eixo y.$

$\displaystyle V = \int_0^1 \pi\left( 1^2 - \left( x^4\right)^2\right)\, dx = \int_0^1 \pi\left( 1 - x^8\right)\, dx \quad = \quad \frac{8π}{9}$unidades ³

21)$ y=\sqrt{x},\quad x=0,\quad x=4,$ e$ y=0$

22)$ y=\sin x,\quad y=\cos x,$ e$ x=0$

Resposta

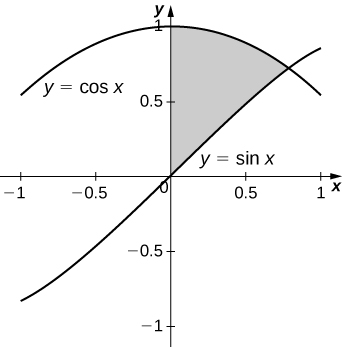
$Esta figura é uma região sombreada delimitada acima pela curva y=cos (x), abaixo à esquerda pelo eixo y e abaixo à direita por y=sin (x). A região sombreada está no primeiro quadrante.$

$\displaystyle V = \int_0^{\pi/4} \pi \left( \cos^2 x - \sin^2 x\right) \, dx = \int_0^{\pi/4} \pi \cos 2x \, dx \quad=\quad \frac{π}{2}$unidades ³

23)$ y=\dfrac{1}{x},\quad x=2$, e$ y=3$

24)$ x^2−y^2=9$ e$ x+y=9,\quad y=0$ e$ x=0$

Resposta

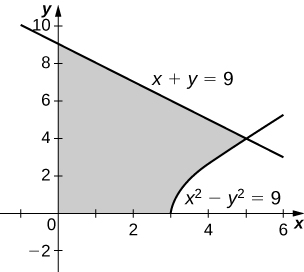
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela linha x + y=9, abaixo pelo eixo x, à esquerda pelo eixo y e à esquerda pela curva x^2-y^2=9.$

$V = 207π$unidades ³

Para os exercícios 25 a 32, desenhe a região delimitada pelas curvas. Em seguida, encontre o volume quando a região for girada em torno do$y$ eixo.

25)$ y=4−\dfrac{1}{2}x,\quad x=0,$ e$ y=0$

26)$ y=2x^3,\quad x=0,\quad x=1,$ e$ y=0$

Resposta

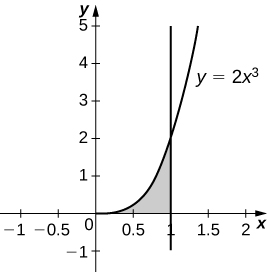
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela curva y=2x^3, abaixo pelo eixo x e à direita pela linha x=1.$

$V = \frac{4π}{5}$unidades ³

27)$ y=3x^2,\quad x=0,$ e$ y=3$

28)$ y=\sqrt{4−x^2},\quad y=0,$ e$ x=0$

Resposta

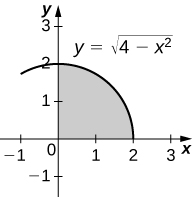
$Esta figura é um gráfico no primeiro quadrante. É um quarto de círculo com centro na origem e raio de 2. Está sombreado por dentro.$

$V = \frac{16π}{3}$unidades ³

29)$ y=\dfrac{1}{\sqrt{x+1}},\quad x=0$, e$ x=3$

30)$ x=\sec(y)$ e$ y=\dfrac{π}{4},\quad y=0$ e$ x=0$

Resposta

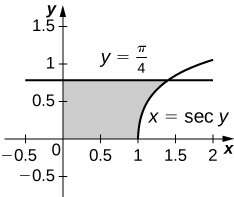
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela linha y=pi/4, à direita pela curva x=sec (y), abaixo pelo eixo x e à esquerda pelo eixo y.$

$V = π$unidades ³

31)$ y=\dfrac{1}{x+1},\quad x=0$, e$ x=2$

32)$ y=4−x,\quad y=x,$ e$ x=0$

Resposta

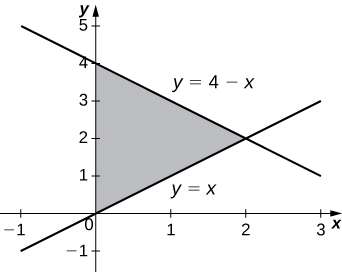
$Esta figura é um gráfico no primeiro quadrante. É um triângulo sombreado limitado acima pela linha y=4-x, abaixo pela linha y=x e à esquerda pelo eixo y.$

$V = \frac{16π}{3}$unidades ³

Para os exercícios 33 a 40, desenhe a região delimitada pelas curvas. Em seguida, encontre o volume quando a região for girada em torno do$x$ eixo.

33)$ y=x+2,\quad y=x+6,\quad x=0$ e$ x=5$

34)$ y=x^2$ e$ y=x+2$

Resposta

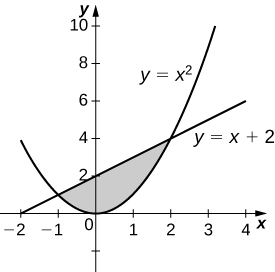
$Esta figura é um gráfico acima do eixo x. É uma região sombreada delimitada acima pela linha y=x+2 e abaixo pela parábola y=x^2.$

$V = \frac{72π}{5}$unidades ³

35)$ x^2=y^3$ e$ x^3=y^2$

36)$ y=4−x^2$ e$ y=2−x$

Resposta

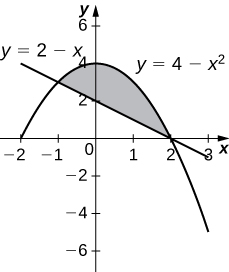
$Esta figura é uma região sombreada delimitada acima pela curva y=4-x^2 e abaixo pela linha y=2-x.$

$V = \frac{108π}{5}$unidades ³

37) [T]$ y=\cos x,\quad y=e^{−x},\quad x=0$ e$ x=1.2927$

38)$ y=\sqrt{x}$ e$ y=x^2$

Resposta

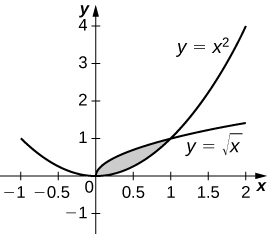
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela curva y=raiz quadrada (x), abaixo pela curva y=x^2.$

$V = \frac{3π}{10}$unidades ³

39)$ y=\sin x,\quad y=5\sin x,\quad x=0$ e$ x=π$

40)$ y=\sqrt{1+x^2}$ e$ y=\sqrt{4−x^2}$

Resposta

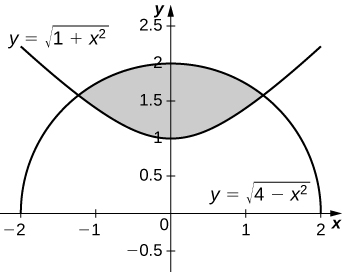
$Esta figura é uma região sombreada delimitada acima pela curva y=raiz quadrada (4-x^2) e, abaixo, pela curva y=raiz quadrada (1+x^2).$

$V = 2\sqrt{6}π$unidades ³

Para os exercícios 41 a 45, desenhe a região delimitada pelas curvas. Em seguida, use o método de lavagem para encontrar o volume quando a região é girada em torno do$y$ eixo.

41)$ y=\sqrt{x},\quad x=4$, e$ y=0$

42)$ y=x+2,\quad y=2x−1$, e$ x=0$

Resposta

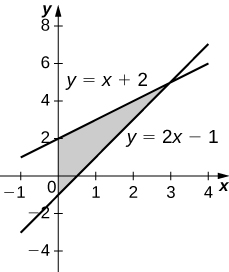
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela linha y=x+2, abaixo pela linha y=2x-1 e à esquerda pelo eixo y.$

$V = 9π$unidades ³

43)$ y=\dfrac{3}{x}$ e$ y=x^3$

44)$ x=e^{2y},\quad x=y^2,\quad y=0$, e$ y=\ln(2)$

Resposta

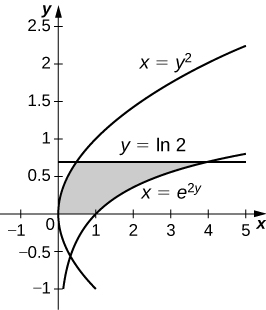
$Esta figura é um gráfico no primeiro quadrante. É uma região sombreada delimitada acima pela curva y=ln (2), abaixo pelo eixo x, à esquerda pela curva x=y^2 e à direita pela curva x=e^ (2y).$

$V = \dfrac{π}{20}(75−4\ln^5(2))$unidades ³

45)$ x=\sqrt{9−y^2},\quad x=e^{−y},\quad y=0$ e$ y=3$

46) Os recipientes de iogurte podem ter a forma de frustums. Gire a linha$ y=\left(\frac{1}{m}\right)x$ ao redor do$y$ eixo -para encontrar o volume entre$ y=a$$ y=b$ e.

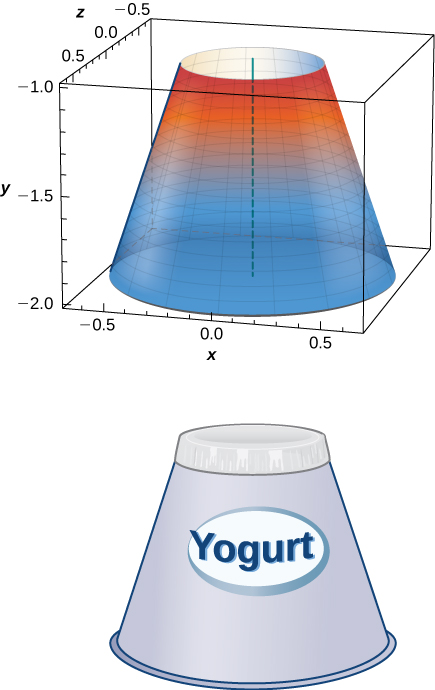
$Essa figura tem duas partes. A primeira parte é um cone sólido. A base do cone é mais larga que a parte superior. É mostrado em uma caixa tridimensional. Embaixo do cone está a imagem de um recipiente de iogurte com o mesmo formato da figura.$

Resposta: $V = \dfrac{m^2π}{3}(b^3−a^3)$unidades ³

47) Gire a elipse$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ ao redor do$x$ eixo -para aproximar o volume de uma bola de futebol, como visto aqui.

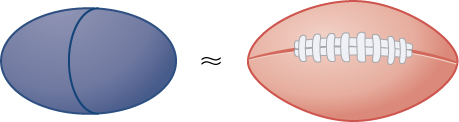
$Esta figura tem um oval que é aproximadamente igual à imagem de uma bola de futebol.$

48) Gire a elipse$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ ao redor do$y$ eixo -para aproximar o volume de uma bola de futebol.

Resposta: $V = \frac{4a^2bπ}{3}$unidades ³

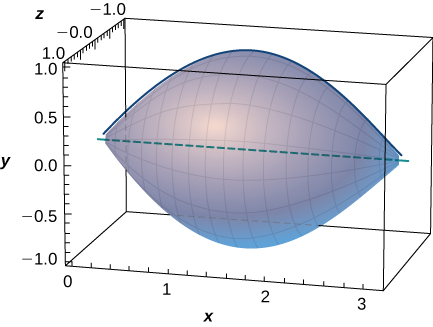
49) Uma melhor aproximação do volume de uma bola de futebol é dada pelo sólido que vem da rotação do$ y=\sin x) around the \(x$ eixo$ x=0$ -de$ x=π$ a. Qual é o volume dessa aproximação do futebol, como visto aqui?

$Esta figura tem uma forma oval tridimensional. Ele está dentro de uma caixa paralela ao eixo x na borda frontal inferior da caixa. O eixo y é vertical em relação ao sólido.$

Para os exercícios 51 a 56, determine o volume do sólido descrito.

51) A base é a região entre$ y=x$$ y=x^2$ e. As fatias perpendiculares ao$x$ eixo -são semicírculos.

52) A base é a região delimitada pela elipse genérica. As$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.$ fatias perpendiculares ao$x$ eixo -são semicírculos.

Resposta: $V = \frac{2ab^2π}{3}$unidades ³

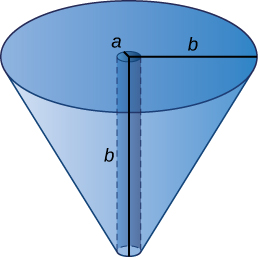
53) Faça um furo de raio a abaixo do eixo do cone$a$ direito e através da base do raio$b$, como visto aqui.

$Esta figura é um cone invertido. Tem um raio do topo como “b”, centro em “a” e altura como “b”.$

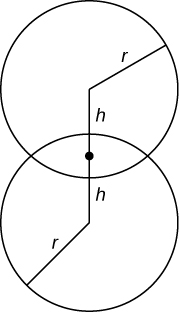
54) Encontre o volume comum a duas esferas de raio$r$ com centros$2h$ separados, conforme mostrado aqui.

$Essa figura tem dois círculos que se cruzam. Ambos os círculos têm raio “r”. Há um segmento de linha de um centro para o outro. No meio da interseção dos círculos está o ponto “h”. Está no segmento da linha.$

Resposta: $V = \frac{π}{12}(r+h)^2(6r−h)$unidades ³

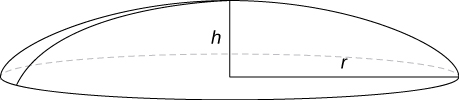
55) Encontre o volume de uma capa esférica de altura$h$ e raio$r$ onde$h<r$, como visto aqui.

$Esta figura é uma parte de uma esfera. Essa capa esférica tem raio “r” e altura “h”.$

56) Encontre o volume de uma esfera de raio$R$ com uma tampa de altura$h$ removida da parte superior, como visto aqui.

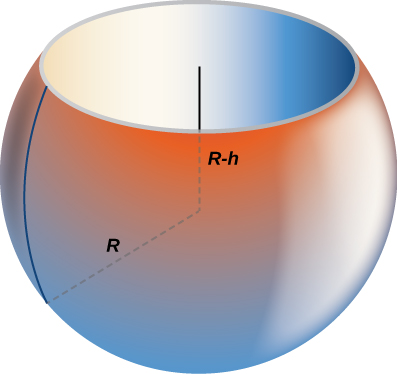
$Esta figura é uma esfera com uma parte superior removida. O raio da esfera é “R”. A distância do centro até onde a parte superior é removida é “R-h”.$

Resposta: $V = \dfrac{π}{3}(h+R)(h−2R)^2$unidades ³

Colaboradores

Template:ContribOpenStaxCalc