6.2: Determinando volumes por fatiamento

Last updated
Save as PDF

Page ID: 187840

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Determine o volume de um sólido integrando uma seção transversal (o método de fatiamento).
Encontre o volume de um sólido de revolução usando o método do disco.
Encontre o volume de um sólido de revolução com uma cavidade usando o método de lavagem.

Na seção anterior, usamos integrais definidas para encontrar a área entre duas curvas. Nesta seção, usamos integrais definidas para encontrar volumes de sólidos tridimensionais. Consideramos três abordagens — fatiamento, discos e arruelas — para encontrar esses volumes, dependendo das características do sólido.

Volume e o método de corte

Assim como a área é a medida numérica de uma região bidimensional, o volume é a medida numérica de um sólido tridimensional. A maioria de nós calculou volumes de sólidos usando fórmulas geométricas básicas. O volume de um sólido retangular, por exemplo, pode ser calculado multiplicando o comprimento, a largura e a altura:$V=lwh.$ As fórmulas para os volumes de:

uma esfera

\[V_{sphere}=\dfrac{4}{3}πr^3, \nonumber \]

um cone

\[V_{cone}=\dfrac{1}{3}πr^2h \nonumber \]

e uma pirâmide

\[V_{pyramid}=\dfrac{1}{3}Ah \nonumber \]

também foram introduzidos. Embora algumas dessas fórmulas tenham sido derivadas usando apenas a geometria, todas essas fórmulas podem ser obtidas usando a integração.

Também podemos calcular o volume de um cilindro. Embora a maioria de nós pense que um cilindro tem uma base circular, como uma lata de sopa ou uma haste de metal, em matemática a palavra cilindro tem um significado mais geral. Para discutir os cilindros nesse contexto mais geral, primeiro precisamos definir algum vocabulário.

Definimos a seção transversal de um sólido como sendo a interseção de um plano com o sólido. Um cilindro é definido como qualquer sólido que pode ser gerado ao traduzir uma região plana ao longo de uma linha perpendicular à região, chamada eixo do cilindro. Assim, todas as seções transversais perpendiculares ao eixo de um cilindro são idênticas. O sólido mostrado na Figura$\PageIndex{1}$ é um exemplo de cilindro com base não circular. Para calcular o volume de um cilindro, simplesmente multiplicamos a área da seção transversal pela altura do cilindro:$V=A⋅h.$ no caso de um cilindro circular reto (lata de sopa), isso se torna$V=πr^2h.$

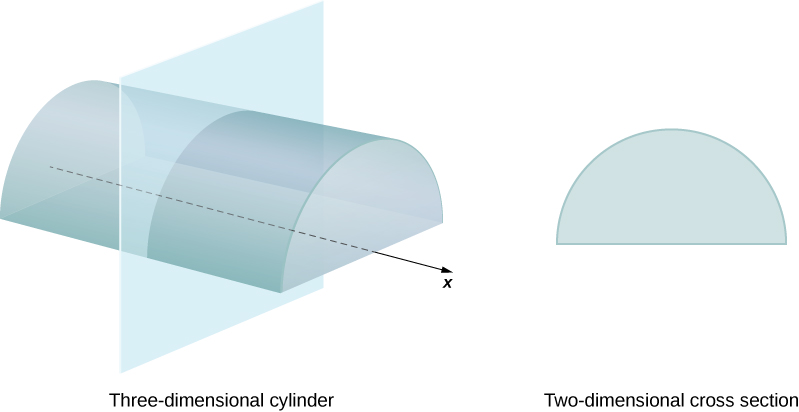
Este gráfico tem duas figuras. A primeira figura é metade de um cilindro, na parte plana. O cilindro tem uma linha no centro chamada “x”. Cortar verticalmente o cilindro, perpendicular à linha, é um plano. A segunda figura é uma seção transversal bidimensional do cilindro que se cruza com o plano. É um semicírculo. — Figura$\PageIndex{1}$*: Cada seção transversal de um cilindro específico é idêntica às outras.*

Se um sólido não tiver uma seção transversal constante (e não for um dos outros sólidos básicos), talvez não tenhamos uma fórmula para seu volume. Nesse caso, podemos usar uma integral definida para calcular o volume do sólido. Fazemos isso cortando o sólido em pedaços, estimando o volume de cada fatia e, em seguida, adicionando esses volumes estimados. As fatias devem estar todas paralelas umas às outras e, quando juntamos todas as fatias, devemos obter todo o sólido. Considere, por exemplo, o sólido S mostrado na Figura$\PageIndex{2}$, que se estende ao longo do$x$ eixo.

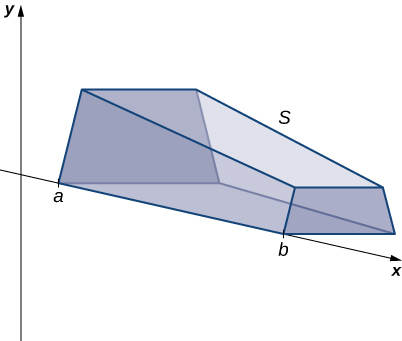
Esta figura é um gráfico de um sólido tridimensional. Tem uma aresta ao longo do eixo x. O eixo x faz parte do sistema de coordenadas bidimensional com o eixo y rotulado. A borda do sólido ao longo do eixo x começa em um ponto rotulado como “a” e para em um ponto rotulado como “b”. — Figura$\PageIndex{2}$: Um sólido com uma seção transversal variável.

Queremos$S$ dividir em fatias perpendiculares $x$ao eixo. Como vemos mais adiante no capítulo, pode haver momentos em que desejamos cortar o sólido em alguma outra direção, por exemplo, com fatias perpendiculares ao$y$ eixo. A decisão de como cortar o sólido é muito importante. Se fizermos a escolha errada, os cálculos podem ficar muito confusos. Mais adiante neste capítulo, examinaremos algumas dessas situações em detalhes e veremos como decidir de que forma cortar o sólido. Para os propósitos desta seção, no entanto, usamos fatias perpendiculares ao$x$ eixo.

Como a área da seção transversal não é constante, vamos$A(x)$ representar a área da seção transversal no ponto x. Agora,$P={x_0,x_1…,X_n}$ seja uma partição regular de$[a,b]$, e para$i=1,2,…n$, vamos$S_i$ representar a fatia de$S$ alongamento de$x_{i−1}$ até$x_i$. A figura a seguir mostra o sólido fatiado com$n=3$.

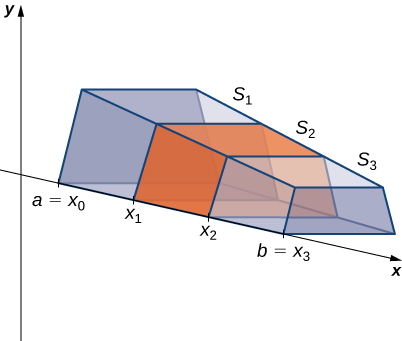
Finalmente, pois$i=1,2,…n,$$x^∗_i$ sejamos um ponto arbitrário$[x_{i−1},x_i]$. Em seguida, o volume da fatia$S_i$ pode ser estimado por$V(S_i)≈A(x^∗_i)\,Δx$. Somando essas aproximações, vemos que o volume de todo o sólido$S$ pode ser aproximado por

\[V(S)≈\sum_{i=1}^nA(x^∗_i)\,Δx. \nonumber \]

Até agora, podemos reconhecer isso como uma soma de Riemann, e nosso próximo passo é tomar o limite como$n→∞.$ Então temos

\[V(S)=\lim_{n→∞}\sum_{i=1}^nA(x^∗_i)\,Δx=∫_a^b A(x)\,dx. \nonumber \]

A técnica que acabamos de descrever é chamada de método de fatiamento. Para aplicá-la, usamos a estratégia a seguir.

Estratégia de resolução de problemas: encontrando volumes pelo método de fatiamento

Examine o sólido e determine a forma de uma seção transversal do sólido. Muitas vezes, é útil fazer um desenho se não for fornecido.
Determine uma fórmula para a área da seção transversal.
Integre a fórmula da área no intervalo apropriado para obter o volume.

Lembre-se de que, nesta seção, assumimos que as fatias são perpendiculares ao$x$ eixo. Portanto, a fórmula da área é em termos de x e os limites de integração estão no $x$eixo y. No entanto, a estratégia de resolução de problemas mostrada aqui é válida independentemente de como escolhermos cortar o sólido.

Exemplo$\PageIndex{1}$: Deriving the Formula for the Volume of a Pyramid

Sabemos pela geometria que a fórmula para o volume de uma pirâmide é$V=\dfrac{1}{3}Ah$. Se a pirâmide tiver uma base quadrada$V=\dfrac{1}{3}a^2h$, isso se torna, onde a indica o comprimento de um lado da base. Vamos usar o método de fatiamento para derivar essa fórmula.

Solução

Queremos aplicar o método de corte a uma pirâmide com base quadrada. Para configurar a integral, considere a pirâmide mostrada na Figura$\PageIndex{4}$, orientada ao longo do $x$eixo.

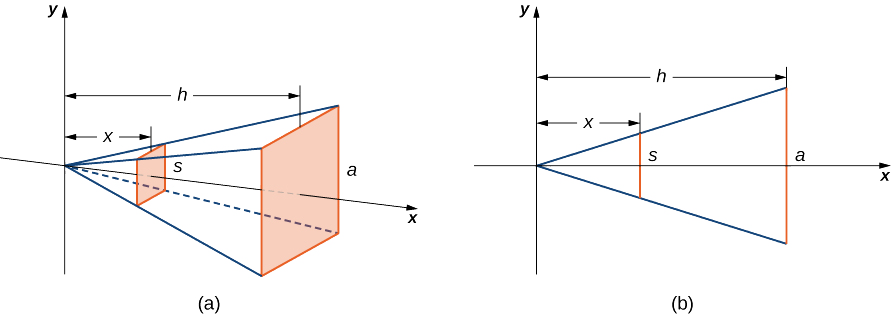
Essa figura tem dois gráficos. O primeiro gráfico, denominado “a”, é uma pirâmide lateral. O eixo x passa pelo meio da pirâmide. O ponto do topo da pirâmide está na origem do sistema de coordenadas x y. A base da pirâmide é sombreada e rotulada como “a”. Dentro da pirâmide há um retângulo sombreado chamado “s”. A distância do eixo y até a base da pirâmide é rotulada como “h”. A distância entre o retângulo dentro da pirâmide e o eixo y é rotulada como “x”. A segunda figura é uma seção transversal da pirâmide com os eixos x e y rotulados. A seção transversal é um triângulo com um lado rotulado como “a”, perpendicular ao eixo x. A distância a do eixo y é h. Há outra linha perpendicular ao eixo x dentro do triângulo. É rotulado como “s”. Está a x unidades do eixo y. — Figura$\PageIndex{4}$: (a) Uma pirâmide com base quadrada é orientada ao longo do$x$ eixo. (b) Uma visão bidimensional da pirâmide é vista de lado.

Primeiro, queremos determinar a forma de uma seção transversal da pirâmide. Sabemos que a base é um quadrado, então as seções transversais também são quadradas (etapa 1). Agora, queremos determinar uma fórmula para a área de um desses quadrados transversais. Olhando para a Figura$\PageIndex{4}$ (b), e usando uma proporção, uma vez que esses são triângulos semelhantes, temos

\[\dfrac{s}{a}=\dfrac{x}{h} \nonumber \]

\[s=\dfrac{ax}{h}. \nonumber \]

Portanto, a área de um dos quadrados transversais é

\[A(x)=s^2=\left(\dfrac{ax}{h}\right)^2 \quad\quad\text{(step 2)} \nonumber \]

Em seguida, encontramos o volume da pirâmide integrando de$0$ a$h$ (etapa 3):

\[V=∫_0^hA(x)\,dx=∫_0^h\left(\dfrac{ax}{h}\right)^2\,dx=\dfrac{a^2}{h^2}∫_0^hx^2\,dx=\left.\Big[\dfrac{a^2}{h^2}\left(\dfrac{1}{3}x^3\right)\Big]\right|^h_0=\dfrac{1}{3}a^2h. \nonumber \]

Essa é a fórmula que procurávamos.

Exercício$\PageIndex{1}$

Use o método de corte para derivar a fórmula\[V=\dfrac{1}{3}πr^2h \nonumber \] para o volume de um cone circular.

Dica: Use triângulos semelhantes, como em Example$\PageIndex{1}$.

Sólidos da Revolução

Se uma região em um plano é girada em torno de uma linha nesse plano, o sólido resultante é chamado de sólido de revolução, conforme mostrado na figura a seguir.

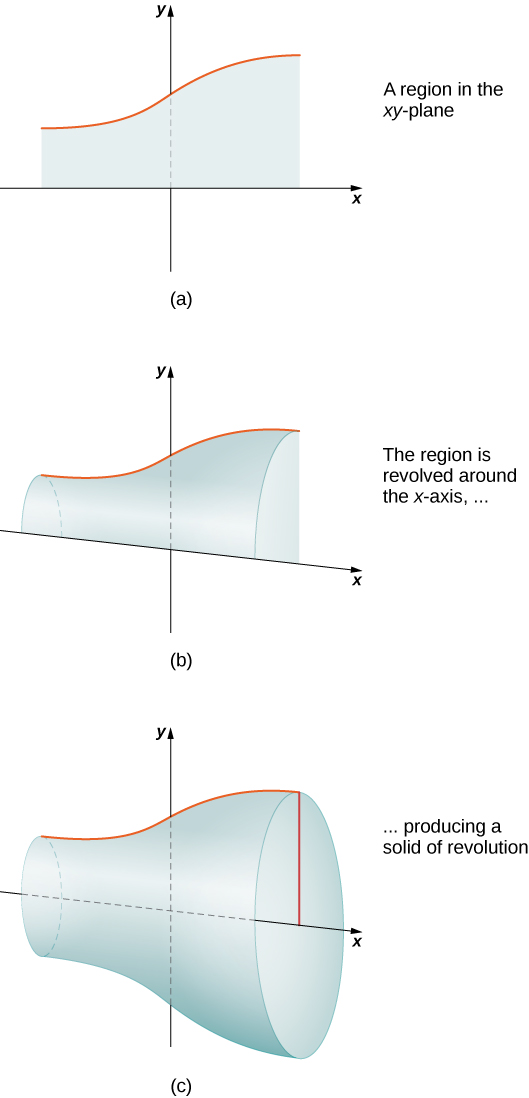
Essa figura tem três gráficos. O primeiro gráfico, denominado “a”, é uma região no plano x y. A região é criada por uma curva acima do eixo x e do eixo x. O segundo gráfico, chamado “b”, é a mesma região de “a”, mas mostra a região começando a girar em torno do eixo x. O terceiro gráfico, denominado “c”, é o sólido formado pela rotação da região de “a” completamente em torno do eixo x, formando um sólido. — Figura$\PageIndex{5}$: (a) Essa é a região que gira em torno do$x$ eixo. (b) Quando a região começa a girar em torno do eixo, ela varre um sólido de revolução. (c) Esse é o sólido que resulta quando a revolução está completa.

Os sólidos de revolução são comuns em aplicações mecânicas, como peças de máquinas produzidas por um torno. Passamos o resto desta seção examinando sólidos desse tipo. O próximo exemplo usa o método de fatiamento para calcular o volume de um sólido de revolução.

Exemplo$\PageIndex{2}$: Using the Slicing Method to find the Volume of a Solid of Revolution

Use o método de fatiamento para encontrar o volume do sólido de revolução limitado pelos gráficos de$f(x)=x^2−4x+5,x=1$ e$x=4,$ e girado em torno do$x$ eixo.

Solução

Usando a estratégia de resolução de problemas, primeiro esboçamos o gráfico da função quadrática ao longo do intervalo$[1,4]$, conforme mostrado na figura a seguir.

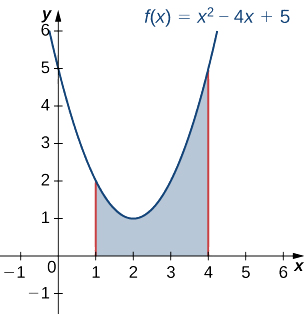
Esta figura é um gráfico da parábola f (x) =x^2-4x+5. A parábola é a parte superior de uma região sombreada acima do eixo x. A região é limitada à esquerda por uma linha em x=1 e à direita por uma linha em x=4. — Figura$\PageIndex{6}$: Uma região usada para produzir um sólido de revolução.

Em seguida, gire a região em torno do$x$ eixo -, conforme mostrado na figura a seguir.

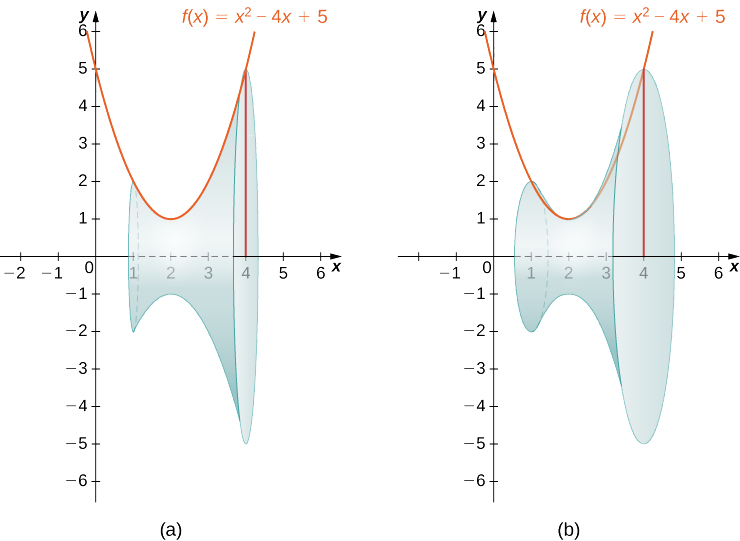
Esta figura tem dois gráficos da parábola f (x) =x^2-4x+5. A parábola é a parte superior de uma região sombreada acima do eixo x. A região é limitada à esquerda por uma linha em x=1 e à direita por uma linha em x=4. O primeiro gráfico tem um sólido sombreado abaixo da parábola. Esse sólido foi formado girando a parábola ao redor do eixo x. O segundo gráfico é igual ao primeiro, com o sólido sendo girado para mostrar o sólido. — Figura$\PageIndex{7}$: Duas vistas, (a) e (b), do sólido da revolução produzido pela rotação da região na Figura em$\PageIndex{6}$ torno do$x$ **eixo.**

Como o sólido foi formado pela rotação da região ao redor do$x$ eixo -, as seções transversais são círculos (etapa 1). A área da seção transversal, então, é a área de um círculo, e o raio do círculo é dado por$f(x).$ Use a fórmula para a área do círculo:

\[A(x)=πr^2=π[f(x)]^2=π(x^2−4x+5)^2\quad\quad\text{(step 2).} \nonumber \]

O volume, então, é (etapa 3)

\[\begin{align*} V &=∫_a^b A(x)\,dx \\ &=∫^4_1π(x^2−4x+5)^2\,dx \\ &=π∫^4_1(x^4−8x^3+26x^2−40x+25)\,dx \\ &=\left. π\left(\dfrac{x^5}{5}−2x^4+\dfrac{26x^3}{3}−20x^2+25x\right)\right|^4_1 \\ &=\dfrac{78}{5}π \end{align*}\]

O volume é$78π/5\,\text{units}^3.$

Exercício$\PageIndex{2}$

Use o método de fatiar para encontrar o volume do sólido de revolução formado pela rotação da região entre o gráfico da função$f(x)=1/x$ e o$x$ eixo -ao longo do intervalo$[1,2]$ ao redor do$x$ eixo. Veja a figura a seguir.

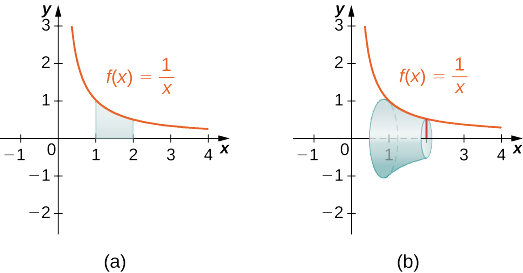
$Essa figura tem dois gráficos. O primeiro gráfico é a curva f (x) =1/x. É uma curva decrescente, acima do eixo x no primeiro quadrante. O gráfico tem uma região sombreada sob a curva entre x=1 e x=2. O segundo gráfico é a curva f (x) =1/x no primeiro quadrante. Além disso, abaixo desse gráfico, há um sólido entre x=1 e x=2 que foi formado pela rotação da região do primeiro gráfico em torno do eixo x.$

Dica: Use a estratégia de resolução de problemas apresentada anteriormente e siga$\PageIndex{2}$ o exemplo para ajudar na etapa 2.

Resposta: $\dfrac{π}{2} \,\text{units}^3$

O método de disco

Quando usamos o método de fatiamento com sólidos de revolução, geralmente é chamado de método de disco porque, para sólidos de revolução, as fatias usadas para aproximar demais o volume do sólido são discos. Para ver isso, considere o sólido da revolução gerado pela rotação da região entre o gráfico da função$f(x)=(x−1)^2+1$ e o $x$eixo -ao longo do intervalo$[−1,3]$ ao redor do$x$ eixo. O gráfico da função e um disco representativo são mostrados nas Figuras$\PageIndex{8}$ (a) e (b). A região de revolução e o sólido resultante são mostrados nas Figuras$\PageIndex{8}$ (c) e (d).

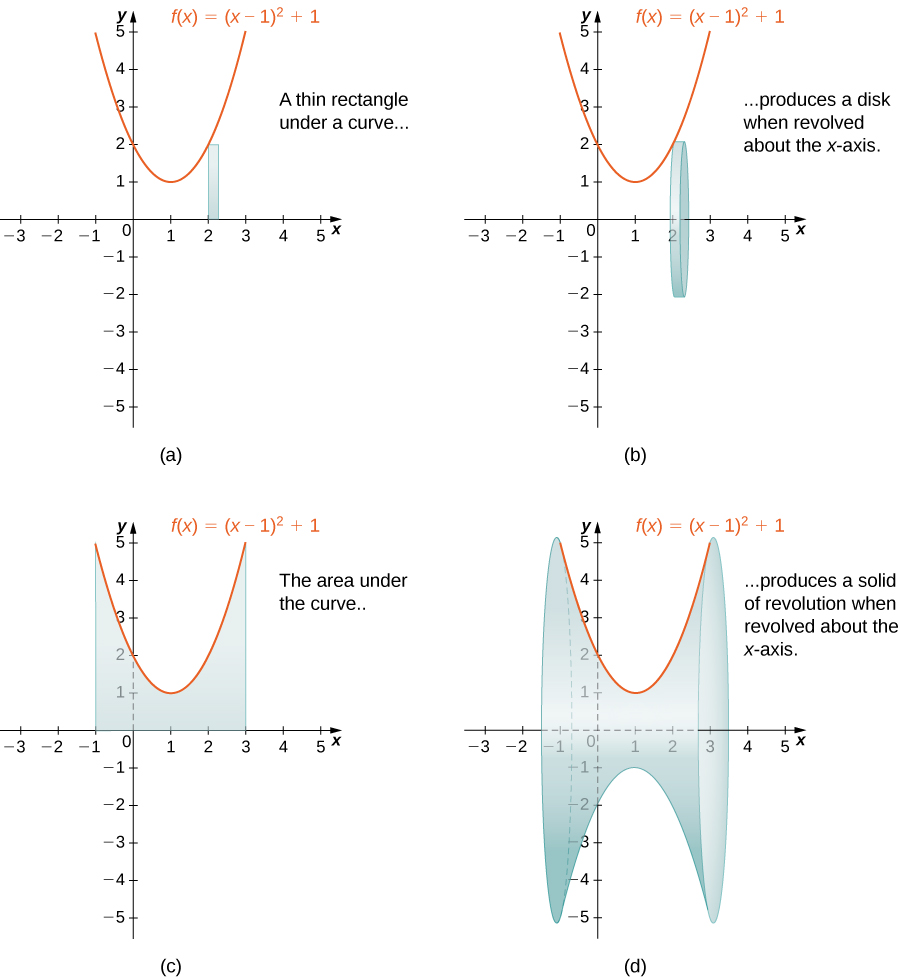
Essa figura tem quatro gráficos. O primeiro gráfico, denominado “a”, é uma parábola f (x) = (x-1) ^2+1. A curva está acima do eixo x e cruza o eixo y em y=2. Abaixo da curva no primeiro quadrante há um retângulo vertical começando no eixo x e parando na curva. O segundo gráfico, denominado “b”, é a mesma parábola do primeiro gráfico. O retângulo sob a parábola do primeiro gráfico foi girado em torno do eixo x formando um disco sólido. O terceiro gráfico chamado “c” é a mesma parábola do primeiro gráfico. Há uma região sombreada delimitada acima pela parábola, à esquerda pela linha x=-1 e à direita pela linha x=3 e abaixo pelo eixo x. O quarto gráfico chamado “d” é a mesma parábola do primeiro gráfico. A região do terceiro gráfico foi girada em torno do eixo x para formar um sólido. — Figura$\PageIndex{8}$: (a) Um retângulo fino para aproximar a área sob uma curva. (b) Um disco representativo formado pela rotação do retângulo em torno do$x$ **eixo.** (c) A região abaixo da curva é girada em torno do$x$ **eixo -,** resultando em (d) o sólido da revolução.

Figura$\PageIndex{8}$: (e) Uma versão dinâmica desse sólido de revolução gerado usando Calcplot3d.

Já usamos o desenvolvimento formal da soma de Riemann da fórmula do volume quando desenvolvemos o método de fatiamento. Nós sabemos disso\[∫_a^b A(x)\,dx.\nonumber \]

A única diferença com o método do disco é que conhecemos a fórmula da área da seção transversal com antecedência; é a área de um círculo. Isso dá a seguinte regra.

O método de disco

$f(x)$Seja contínuo e não negativo. Defina$R$ como a região delimitada acima pelo gráfico de$f(x)$, abaixo pelo$x$ eixo$x=a$ -, à esquerda pela linha e à direita pela linha$x=b$. Então, o volume do sólido de revolução formado pela rotação$R$ em torno do$x$ eixo -é dado por

\[V=∫^b_aπ[f(x)]^2\,dx. \nonumber \]

O volume do sólido que estamos estudando (Figura$\PageIndex{8}$) é dado por

\ [\ begin {align*} V &=^b_aπ\ esquerda [f (x)\ direita] ^2\, dx\\
&=^3_ {−1} π\ grande [(x−1) ^2+1\ grande] ^2\, dx=π ^3_ {−1}\ big [(x−1) ^4+2 (x−1) ^2+1\ big] ^2\, dx\\
&=π\ left. \ Big [\ frac {1} {5} (x−1) ^5+\ frac {2} {3} (x−1) ^3+x\ Big]\ right|^3_ {−1}\\
&=π\ left [\ left (\ frac {32} {5} +\ frac {16} {3} +3\ direita) −\ left (\ frac −\ frac {32} {5} −\ frac {16} {3} −1\ right)\ right]\\
&=\ frac {412π} {15}\,\ texto {unidades} ^3. \ end {align*}\]

Vejamos alguns exemplos.

Exemplo$\PageIndex{3}$: Using the Disk Method to Find the Volume of a Solid of Revolution 1

Use o método do disco para encontrar o volume do sólido de revolução gerado pela rotação da região entre o gráfico de$f(x)=\sqrt{x}$ e o$x$ eixo -ao longo do intervalo$[1,4]$ em torno do$x$ eixo.

Solução

Os gráficos da função e do sólido da revolução são mostrados na figura a seguir.

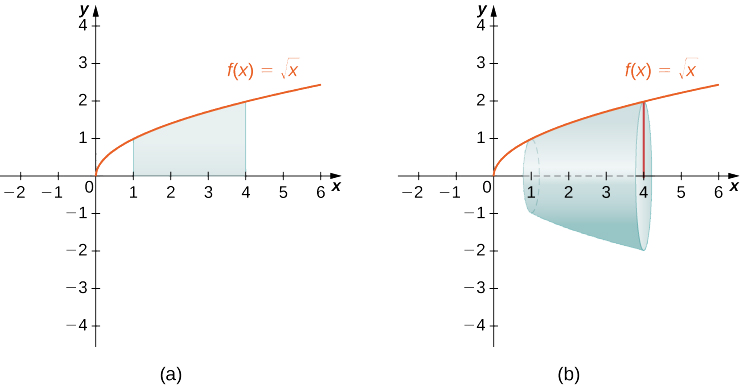
Essa figura tem dois gráficos. O primeiro gráfico chamado “a” é a curva f (x) = raiz quadrada (x). É uma curva crescente acima do eixo x. A curva está no primeiro quadrante. Abaixo da curva está uma região limitada por x=1 e x=4. A parte inferior da região é o eixo x. O segundo gráfico chamado “b” é a mesma curva do primeiro gráfico. A região sólida do primeiro gráfico foi girada em torno do eixo x para formar uma região sólida. — Figura$\PageIndex{9}$: (a) A função$f(x)=\sqrt{x}$ no intervalo$[1,4]$. (b) O sólido da revolução obtido pela rotação da região sob o gráfico de$f(x)$ cerca do$x$ **eixo**.

Nós temos

\ [\ begin {align*} V&=^B_Aπ\ big [f (x)\ big] ^2\, dx\\
&=^4_1π\ esquerda [\ sqrt {x}\ direita] ^2\, dx=π ^4_1x\, dx\\ &=\ dfrac {π} {2} x^2\ bigg|^4_1x\, dx\\
&=\ dfrac {π} {2} x^2\ bigg|^4 _1=\ dfrac {15π} {2}\ end {align*}\]

O volume é$(15π)/2 \,\text{units}^3.$

Exercício$\PageIndex{3}$

Use o método do disco para encontrar o volume do sólido de revolução gerado pela rotação da região entre o gráfico de$f(x)=\sqrt{4−x}$ e o$x$ eixo -ao longo do intervalo$[0,4]$ em torno do$x$ eixo.

Dica: Use o procedimento do Example$\PageIndex{3}$.

Resposta: $8π \,\text{units}^3$

Até agora, todos os nossos exemplos dizem respeito a regiões giradas em torno do$x$ eixo -, mas podemos gerar um sólido de revolução girando uma região plana em torno de qualquer linha horizontal ou vertical. No próximo exemplo, veremos um sólido de revolução que foi gerado pela rotação de uma região em torno do$y$ eixo. A mecânica do método do disco é quase a mesma de quando o$x$ eixo -é o eixo da revolução, mas expressamos a função em termos de$y$ e também nos integramos em relação a y. Isso está resumido na regra a seguir.

Regra: O método de disco para sólidos de revolução em torno do$y$-axis

$g(y)$Seja contínuo e não negativo. Defina$Q$ como a região delimitada à direita pelo gráfico de$g(y)$, à esquerda pelo$y$ eixo -, abaixo pela linha$y=c$ e acima pela linha$y=d$. Então, o volume do sólido de revolução formado pela rotação$Q$ em torno do$y$ eixo -é dado por

\[V=∫^d_cπ\big[g(y)\big]^2\,dy. \nonumber \]

O próximo exemplo mostra como essa regra funciona na prática.

Exemplo$\PageIndex{4}$: Using the Disk Method to Find the Volume of a Solid of Revolution 2

$R$Seja a região delimitada pelo gráfico de$g(y)=\sqrt{4−y}$ e o$y$ eixo -sobre o intervalo do$y$ eixo$[0,4]$ -. Use o método do disco para encontrar o volume do sólido de revolução gerado pela rotação$R$ em torno do$y$ eixo.

Solução

A figura$\PageIndex{10}$ mostra a função e um disco representativo que pode ser usado para estimar o volume. Observe que, como estamos girando a função em torno do$y$ eixo -, os discos são horizontais, em vez de verticais.

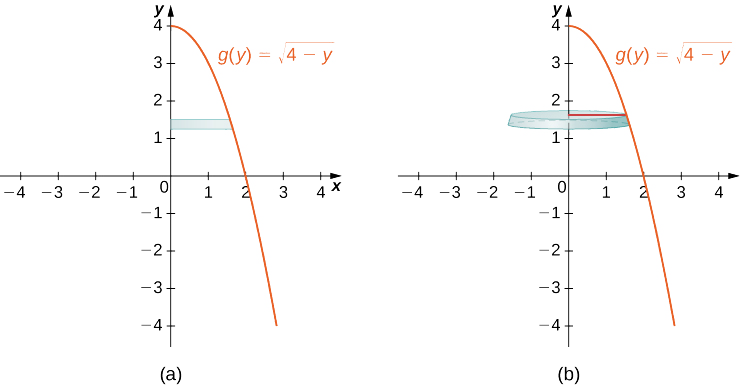
Essa figura tem dois gráficos. O primeiro gráfico chamado “a” é a curva g (y) = raiz quadrada (4-y). É uma curva decrescente começando no eixo y em y=4. Entre a curva e o eixo y há um retângulo horizontal. O retângulo começa no eixo y e para na curva. O segundo gráfico chamado “b” é a mesma curva do primeiro gráfico. O retângulo do primeiro gráfico foi girado em torno do eixo y para formar um disco horizontal. — Figura$\PageIndex{10}$: (a) É mostrado um retângulo fino entre a curva da função$g(y)=\sqrt{4−y}$ e o$y$ **eixo.** (b) O retângulo forma um disco representativo após a revolução em torno do$y$ **eixo.**

A região a ser revolvida e todo o sólido da revolução estão representados na figura a seguir.

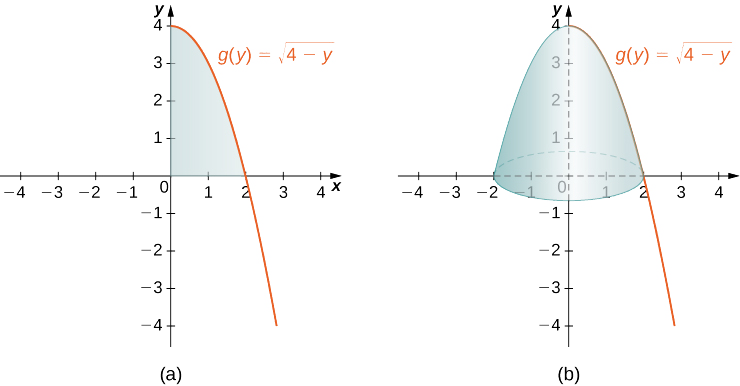
Essa figura tem dois gráficos. O primeiro gráfico chamado “a” é a curva g (y) = raiz quadrada (4-y). É uma curva decrescente começando no eixo y em y=4. A região formada pelo eixo x, pelo eixo y e pela curva é sombreada. Essa região está no primeiro quadrante. O segundo gráfico chamado “b” é a mesma curva do primeiro gráfico. A região do primeiro gráfico foi girada em torno do eixo y para formar um sólido. — Figura$\PageIndex{11}$: (a) A região à esquerda da função no$g(y)=\sqrt{4−y}$ intervalo do$y$ eixo$[0,4]$. (b) O sólido da revolução formado pela rotação da região em torno do$y$ eixo.

Para encontrar o volume, nós nos integramos em relação$y$ a. Nós obtemos

\[V=∫^d_cπ\big[g(y)\big]^2\,dy=∫^4_0π\left[\sqrt{4−y}\right]^2\,dy=π∫^4_0(4−y)\,dy=π\left.\left[4y−\frac{y^2}{2}\right]\right|^4_0=8π. \nonumber \]

O volume é$8π \,\text{units}^3$.

Exercício$\PageIndex{4}$

Use o método do disco para encontrar o volume do sólido de revolução gerado pela rotação da região entre o gráfico de$g(y)=y$ e o$y$ eixo -ao longo do intervalo$[1,4]$ em torno do$y$ eixo.

Dica: Use o procedimento do Example$\PageIndex{4}$.

Resposta: $21π \,\text{units}^3$

O método lavador

Alguns sólidos da revolução têm cavidades no meio; eles não são sólidos até o eixo da revolução. Às vezes, isso é apenas o resultado da forma como a região da revolução é moldada em relação ao eixo da revolução. Em outros casos, cavidades surgem quando a região de revolução é definida como a região entre os gráficos de duas funções. Uma terceira maneira pela qual isso pode acontecer é quando um eixo de revolução diferente do $x$eixo -ou $y$eixo -é selecionado.

Quando o sólido da revolução tem uma cavidade no meio, as fatias usadas para aproximar o volume não são discos, mas arruelas (discos com furos no centro). Por exemplo, considere a região delimitada acima pelo gráfico da função$f(x)=\sqrt{x}$ e abaixo pelo gráfico da função no$g(x)=1$ intervalo$[1,4]$. Quando essa região é girada em torno do$x$ eixo -, o resultado é um sólido com uma cavidade no meio e as fatias são arruelas. O gráfico da função e uma arruela representativa são mostrados nas Figuras$\PageIndex{12}$ (a) e (b). A região de revolução e o sólido resultante são mostrados nas Figuras$\PageIndex{12}$ (c) e (d).

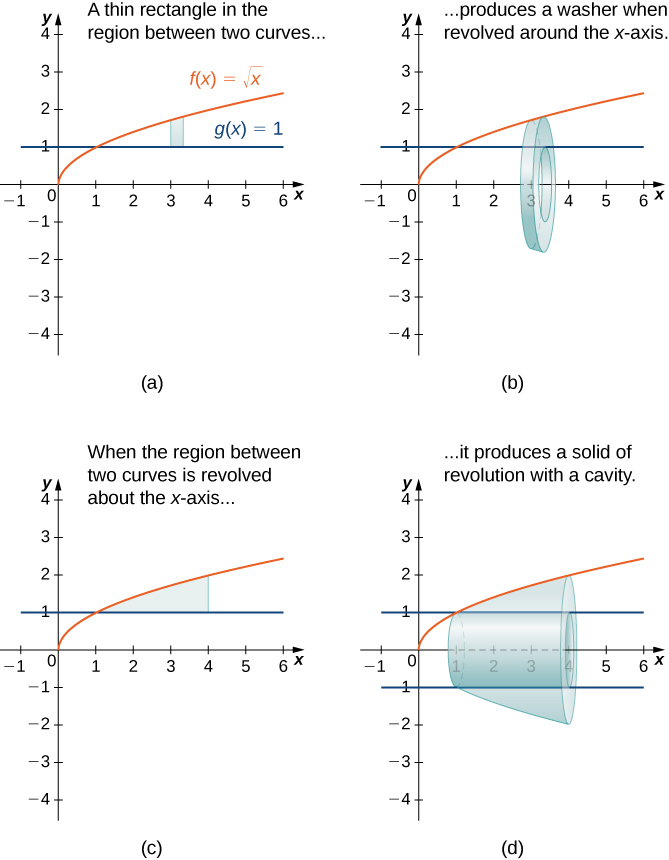
Essa figura tem quatro gráficos. O primeiro gráfico é rotulado como “a” e tem as duas funções f (x) =raiz quadrada (x) e g (x) =1 representadas graficamente no primeiro quadrante. f (x) é uma curva crescente começando na origem e g (x) é uma linha horizontal em y=1. As curvas se cruzam no par ordenado (1,1). Entre as curvas há um retângulo sombreado com a parte inferior em g (x) e a parte superior em f (x). O segundo gráfico chamado “b” tem as mesmas duas curvas do primeiro gráfico. O retângulo sombreado entre as curvas do primeiro gráfico foi girado em torno do eixo x para formar um disco aberto ou uma arruela. O terceiro gráfico chamado “a” tem as mesmas duas curvas do primeiro gráfico. Há uma região sombreada entre as duas curvas entre onde elas se cruzam e uma linha em x=4. O quarto gráfico tem as mesmas duas curvas da primeira, com a região do terceiro gráfico girada em torno do eixo x formando uma região sólida com um centro oco. O centro oco é representado no gráfico com linhas horizontais quebradas em y=1 e y=-1. — Figura$\PageIndex{12}$: (a) Um retângulo fino na região entre duas curvas. (b) Um disco representativo formado pela rotação do retângulo em torno do$x$ **eixo.** (c) A região entre as curvas ao longo do intervalo dado. (d) O sólido resultante da revolução.

Figura$\PageIndex{12}$: (e) Uma versão dinâmica desse sólido de revolução gerado usando Calcplot3d.

A área da seção transversal, então, é a área do círculo externo menos a área do círculo interno. Nesse caso,

$A(x)=π\left(\sqrt{x}\right)^2−π(1)^2=π(x−1).$

Então, o volume do sólido é

\[V=∫^b_a A(x)\,dx=∫^4_1π(x−1)\,dx=π\left.\left[\frac{x^2}{2}−x\right]\right|^4_1=\frac{9}{2}π\,\text{units}^3. \nonumber \]

A generalização desse processo fornece o método de lavagem.

Regra: O método de lavagem

Suponha$f(x)$ e$g(x)$ sejam funções contínuas e não negativas, tais como$f(x)≥g(x)$ terminadas$[a,b]$. Vamos$R$ indicar a região delimitada acima pelo gráfico de$f(x)$, abaixo pelo gráfico de$g(x)$, à esquerda pela linha$x=a$ e à direita pela linha$x=b$. Então, o volume do sólido de revolução formado pela rotação$R$ em torno do$x$ eixo -é dado por

\[V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx. \nonumber \]

Exemplo$\PageIndex{5}$: Using the Washer Method

Encontre o volume de um sólido de revolução formado pela rotação da região delimitada acima pelo gráfico de$f(x)=x$ e abaixo pelo gráfico do$g(x)=1/x$ intervalo$[1,4]$ ao redor do$x$ eixo.

Solução

Os gráficos das funções e do sólido da revolução são mostrados na figura a seguir.

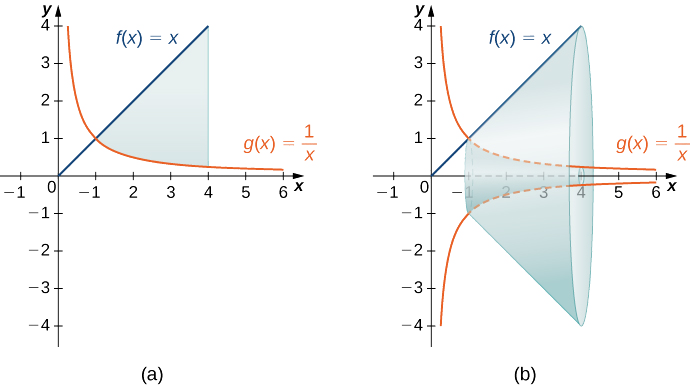
Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e tem as duas curvas f (x) =x e g (x) =1/x. Elas são representadas graficamente somente no primeiro quadrante. f (x) é uma linha diagonal começando na origem e g (x) é uma curva decrescente com o eixo y como assíntota vertical e o eixo x como assíntota horizontal. Os gráficos se cruzam em (1,1). Há uma região sombreada entre os gráficos, limitada à direita por uma linha em x=4. O segundo gráfico tem as mesmas duas curvas. Há um sólido formado pela rotação da região sombreada do primeiro gráfico em torno do eixo x. — Figura$\PageIndex{13}$: (a) A região entre os gráficos das funções$f(x)=x$ e$g(x)=1/x$ ao longo do intervalo$[1,4]$. (b) Girar a região em torno do$x$ **eixo -gera** um sólido de revolução com uma cavidade no meio.

Nós temos

\ [\ begin {align*} V &=^b_aπ\ big [(f (x)) ^2− (g (x)) ^2\ big]\, dx=π ^4_1\ left [x^2−\ left (\ frac {1} {x}\ right) ^2\ right]\, dx\\
&=π\ left. \ left [\ frac {x^3} {3} +\ frac {1} {x}\ right]\ right|^4_1\\
&=\ dfrac {81π} {4}\,\ texto {unidades} ^3. \ end {align*}\]

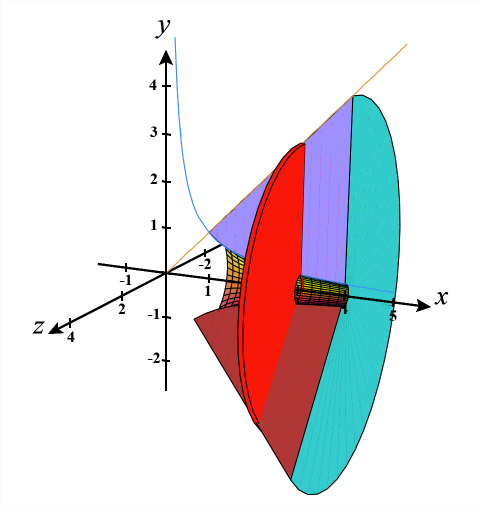
$clipboard_ec285765f5c0a0709a54ba430e31011a6.png$

Figura$\PageIndex{13}$: (c) Uma versão dinâmica desse sólido de revolução gerado usando Calcplot3d.

Exercício$\PageIndex{5}$

Determine o volume de um sólido de revolução formado pela rotação da região delimitada pelos gráficos de$f(x)=\sqrt{x}$ e$g(x)=1/x$ ao longo do intervalo$[1,3]$ ao redor do $x$eixo.

Dica: Faça um gráfico das funções para determinar qual gráfico forma o limite superior e qual gráfico forma o limite inferior e, em seguida, use o procedimento do Example$\PageIndex{5}$.

Resposta: $\dfrac{10π}{3} \,\text{units}^3$

Assim como no método de disco, também podemos aplicar o método de lavagem a sólidos de revolução que resultam da rotação de uma região ao redor do$y$ eixo. Nesse caso, a seguinte regra se aplica.

Regra: O método de lavagem para sólidos de revolução em torno do$y$-axis

Suponha$u(y)$ e$v(y)$ sejam funções contínuas e não negativas, tais como$v(y)≤u(y)$ para$y∈[c,d]$. Vamos$Q$ indicar a região delimitada à direita pelo gráfico de$u(y)$, à esquerda pelo gráfico de$v(y)$, abaixo pela linha$y=c$ e acima pela linha$y=d$. Então, o volume do sólido de revolução formado pela rotação$Q$ em torno do$y$ eixo -é dado por

\[V=∫^d_cπ\left[(u(y))^2−(v(y))^2\right]\,dy. \nonumber \]

Em vez de analisar um exemplo do método lavador com o$y$ eixo -como eixo de revolução, agora consideramos um exemplo em que o eixo de revolução é uma linha diferente de um dos dois eixos coordenados. O mesmo método geral se aplica, mas talvez você precise visualizar exatamente como descrever a área da seção transversal do volume.

Exemplo$\PageIndex{6}$:

Encontre o volume de um sólido de revolução formado pela rotação da região delimitada acima$f(x)=4−x$ e abaixo pelo$x$ eixo -sobre o intervalo$[0,4]$ ao redor da linha$y=−2.$

Solução

O gráfico da região e o sólido da revolução são mostrados na figura a seguir.

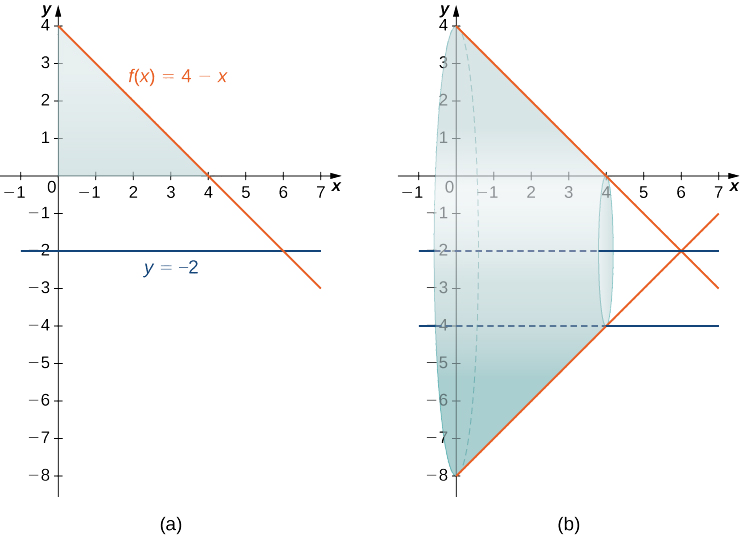
Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e tem as duas curvas f (x) =4-x e -2. Há uma região sombreada formando um triângulo limitado pela linha decrescente f (x), pelo eixo y e pelo eixo x. O segundo gráfico tem as mesmas duas curvas. Há um sólido formado pela rotação da região sombreada do primeiro gráfico em torno da linha y=-2. Há um cilindro oco dentro do sólido representado pelas linhas y=-2 e y=-4. — Figura$\PageIndex{14}$: (a) A região entre o gráfico da função$f(x)=4−x$ e o **$x$eixo -ao** longo do intervalo$[0,4]$. (b) Girar a região ao redor da linha$y=−2$ gera um sólido de revolução com um furo cilíndrico no meio.

Não podemos aplicar a fórmula do volume diretamente a esse problema porque o eixo da revolução não é um dos eixos coordenados. No entanto, ainda sabemos que a área da seção transversal é a área do círculo externo menos a área do círculo interno. Olhando para o gráfico da função, vemos que o raio do círculo externo é dado pelo$f(x)+2,$ qual simplifica para

$f(x)+2=(4−x)+2=6−x.$

O raio do círculo interno é$g(x)=2.$ Portanto, temos

\ [\ begin {align*} V &=^4_0π\ left [(6−x) ^2− (2) ^2\ right]\, dx\\
&=π ^4_0 (x^2−12x+32)\, dx=π\ left. \ left [\ frac {x^3} {3} −6x^2+32x\ right]\ right|^4_0\\
&=\ dfrac {160π} {3}\,\ texto {unidades} ^3. \ end {align*}\]

Figura$\PageIndex{14}$: (c) Uma versão dinâmica desse sólido de revolução gerado usando Calcplot3d.

Exercício$\PageIndex{6}$

Encontre o volume de um sólido de revolução formado pela rotação da região delimitada acima pelo gráfico de$f(x)=x+2$ e abaixo pelo$x$ eixo -sobre o intervalo$[0,3]$ ao redor da linha$y=−1.$

Dica: Use o procedimento do Example$\PageIndex{6}$.

Resposta: $60π$unidades ³

Conceitos chave

Integrais definidas podem ser usadas para encontrar os volumes de sólidos. Usando o método de fatiamento, podemos encontrar um volume integrando a área da seção transversal.
Para sólidos de revolução, as fatias de volume geralmente são discos e as seções transversais são círculos. O método dos discos envolve a aplicação do método de fatiar no caso específico em que as seções transversais são círculos e o uso da fórmula para a área de um círculo.
Se um sólido de revolução tem uma cavidade no centro, as fatias de volume são arruelas. Com o método das arruelas, a área do círculo interno é subtraída da área do círculo externo antes da integração.

Equações chave

Método de disco ao longo do$x$ eixo -

$\displaystyle V=∫^b_aπ\big[f(x)\big]^2\,dx$

Método de disco ao longo do$y$ eixo -

$\displaystyle V=∫^d_cπ\big[g(y)\big]^2\,dy$

Método de lavagem

$\displaystyle V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx$

Glossário

seção transversal: a interseção de um plano e um objeto sólido

método de disco: um caso especial do método de fatiamento usado com sólidos de revolução quando as fatias são discos

método de corte: um método de calcular o volume de um sólido que envolve cortar o sólido em pedaços, estimar o volume de cada peça e, em seguida, adicionar essas estimativas para chegar a uma estimativa do volume total; à medida que o número de fatias vai para o infinito, essa estimativa se torna uma integral que fornece o valor exato do volume

sólido da revolução: um sólido gerado pela rotação de uma região em um plano em torno de uma linha nesse plano

método de lavagem: um caso especial do método de fatiamento usado com sólidos de revolução quando as fatias são arruelas

Estratégia de resolução de problemas: encontrando volumes pelo método de fatiamento

Exemplo\(\PageIndex{1}\): Deriving the Formula for the Volume of a Pyramid

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Using the Slicing Method to find the Volume of a Solid of Revolution

Exercício\(\PageIndex{2}\)

O método de disco

Exemplo\(\PageIndex{3}\): Using the Disk Method to Find the Volume of a Solid of Revolution 1

Exercício\(\PageIndex{3}\)

Regra: O método de disco para sólidos de revolução em torno do\(y\)-axis

Exemplo\(\PageIndex{4}\): Using the Disk Method to Find the Volume of a Solid of Revolution 2

Exercício\(\PageIndex{4}\)

Regra: O método de lavagem

Exemplo\(\PageIndex{5}\): Using the Washer Method

Exercício\(\PageIndex{5}\)

Regra: O método de lavagem para sólidos de revolução em torno do\(y\)-axis

Exemplo\(\PageIndex{6}\):

Exercício\(\PageIndex{6}\)