Skip to main content
Global

6.1E: Exercícios para a Seção 6.1

  1. Last updated
  2. Save as PDF
  • Page ID
    187892

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para os exercícios 1 a 2, determine a área da região entre as duas curvas na figura dada por meio da integração sobre o\(x\) eixo.

    1)\(y=x^2−3\) e\(y=1\)

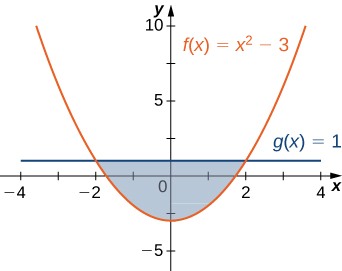
    Esta figura tem dois gráficos. Elas são as funções f (x) = x^2-3 e g (x) =1. Entre esses gráficos está uma região sombreada, delimitada acima por g (x) e abaixo por f (x). A área sombreada está entre x=-2 e x=2.

    Responda
    \(\dfrac{32}{3} \, \text{units}^2\)

    2)\(y=x^2\) e\(y=3x+4\)

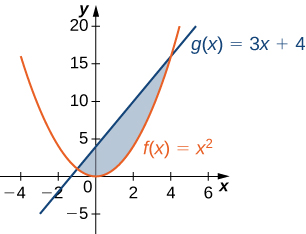
    Esta figura tem dois gráficos. Elas são as funções f (x) = x^2 e g (x) = 3x+4. Entre esses gráficos está uma região sombreada, delimitada acima por g (x) e abaixo por g (x).

    Para os exercícios 3 a 4, divida a região entre as duas curvas em duas regiões menores e, em seguida, determine a área integrando-a sobre o\(x\) eixo. Observe que você terá duas integrais para resolver.

    3)\(y=x^3\) e\( y=x^2+x\)

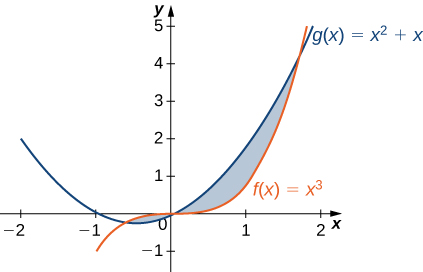
    Esta figura tem dois gráficos. Elas são as funções f (x) = x^3 e g (x) = x^2+x. Esses gráficos se cruzam duas vezes. As regiões entre as interseções estão sombreadas. A primeira região é delimitada acima por f (x) e abaixo por g (x). A segunda região é delimitada acima por g (x) e abaixo por f (x).

    Responda
    \(\dfrac{13}{12}\, \text{units}^2\)

    4)\(y=\cos θ\) e\( y=0.5\), para\( 0≤θ≤π\)

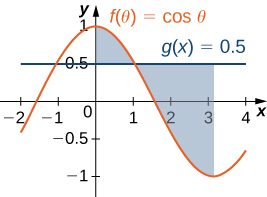
    Esta figura tem dois gráficos. São as funções f (theta) = cos (teta) e g (x) = 0,5. Esses gráficos se cruzam duas vezes. As regiões entre as interseções estão sombreadas. A primeira região é delimitada acima por f (x) e abaixo por g (x). A segunda região é delimitada acima por g (x) e abaixo por f (x).

    Para os exercícios 5-6, determine a área da região entre as duas curvas integrando-as sobre o\(y\) eixo.

    5)\(x=y^2\) e\(x=9\)

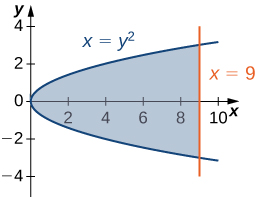
    Esta figura tem dois gráficos. Elas são as equações x=y^2 e x=9. A região entre os gráficos está sombreada. É horizontal, entre o eixo y e a linha x=9.

    Responda
    \(36 \, \text{units}^2\)

    6)\(y=x\) e\( x=y^2\)

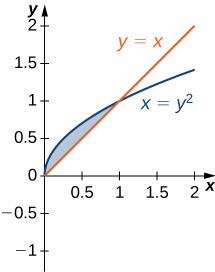
    Esta figura tem dois gráficos. Elas são as equações y=x e x=y^2. A região entre os gráficos é sombreada, delimitada acima por x=y^2 e abaixo por y=x.

    Para os exercícios 7 a 13, faça um gráfico das equações e sombreie a área da região entre as curvas. Determine sua área integrando-a sobre o\(x\) eixo y.

    7)\(y=x^2\) e\(y=−x^2+18x\)

    Responda

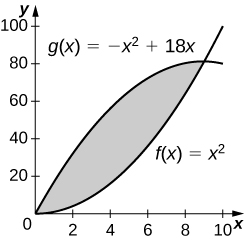
    Esta figura tem dois gráficos. Elas são as funções f (x) =x^2 e g (x) =-x^2+18x. A região entre os gráficos é sombreada, delimitada acima por g (x) e abaixo por f (x). Está no primeiro quadrante.

    243 unidades quadradas

    8)\(y=\dfrac{1}{x}, \quad y=\dfrac{1}{x^2}\) e\(x=3\)

    9)\(y=\cos x\) e\(y=\cos^2x\) sobre\(x \in [−π,π]\)

    Responda

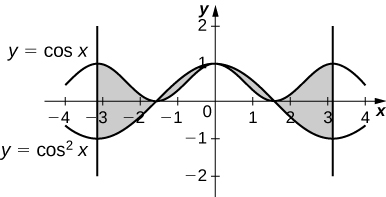
    Esta figura tem dois gráficos. Elas são as funções y=cos (x) e y=cos^2 (x). Os gráficos são periódicos e lembram ondas. Há quatro regiões criadas pelas interseções das curvas. As áreas estão sombreadas.

    4 unidades quadradas

    10)\(y=e^x,\quad y=e^{2x−1}\) e\(x=0\)

    11)\(y=e^x, \quad y=e^{−x}, \quad x=−1\) e\(x=1\)

    Responda

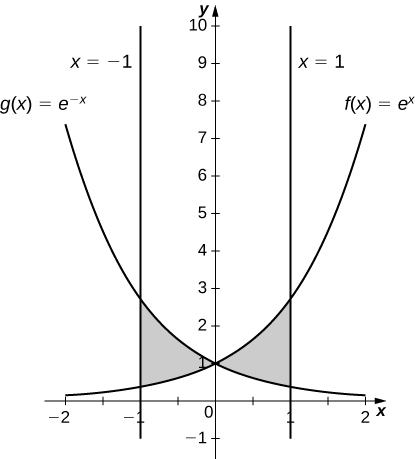
    Esta figura tem dois gráficos. Elas são as funções f (x) =e^x e g (x) =e^-x. Há duas regiões sombreadas. No segundo quadrante, a região é limitada por x=-1, g (x) acima e f (x) abaixo. A segunda região está no primeiro quadrante e é limitada por f (x) acima, g (x) abaixo e x=1.

    \(\dfrac{2(e−1)^2}{e}\, \text{units}^2\)

    12)\( y=e, \quad y=e^x,\) e\(y=e^{−x}\)

    13)\(y=|x|\) e\(y=x^2\)

    Responda

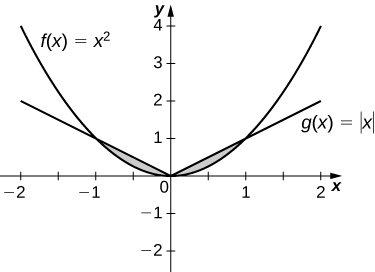
    Esta figura tem dois gráficos. Elas são as funções f (x) =x^2 e g (x) =valor absoluto de x. Existem duas regiões sombreadas. A primeira região está no segundo quadrante e está entre g (x) acima e f (x) abaixo. A segunda região está no primeiro quadrante e é limitada acima por g (x) e abaixo por f (x).

    \(\dfrac{1}{3}\, \text{units}^2\)

    Para os exercícios 14 a 19, faça um gráfico das equações e sombreie a área da região entre as curvas. Se necessário, divida a região em sub-regiões para determinar toda a área.

    14)\(y=\sin(πx),\quad y=2x,\) e\(x>0\)

    15)\(y=12−x,\quad y=\sqrt{x},\) e\(y=1\)

    Responda

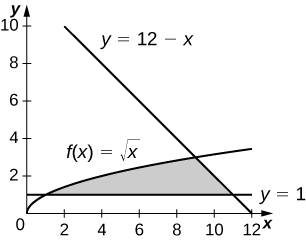
    Esta figura tem três gráficos. Elas são as funções f (x) =raiz quadrada de x, y=12-x e y=1. A região entre os gráficos é sombreada, delimitada acima e à esquerda por f (x), acima e à direita pela linha y=12-x e abaixo pela linha y=1. Está no primeiro quadrante.

    \(\dfrac{34}{3}\, \text{units}^2\)

    16)\(y=\sin x\) e\(y=\cos x\) mais\(x \in [−π,π]\)

    17)\(y=x^3\) e\(y=x^2−2x\) mais\(x \in [−1,1]\)

    Responda

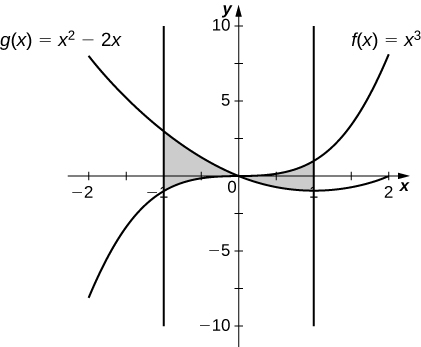
    Esta figura tem dois gráficos. Elas são as funções f (x) =x^3 e g (x) =x^2-2x. Há duas regiões sombreadas entre os gráficos. A primeira região é limitada à esquerda pela linha x=-2, acima por g (x) e abaixo por f (x). A segunda região é delimitada acima por f (x), abaixo por g (x) e à direita pela linha x=2.

    \(\dfrac{5}{2}\, \text{units}^2\)

    18)\(y=x^2+9\) e\( y=10+2x\) mais\(x \in [−1,3]\)

    19)\(y=x^3+3x\) e\(y=4x\)

    Responda

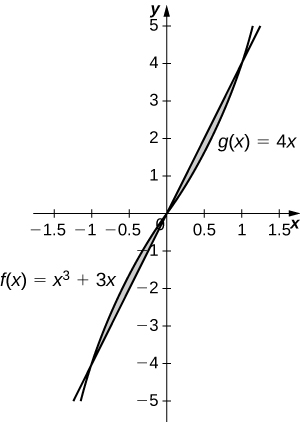
    Esta figura tem dois gráficos. Elas são as funções f (x) =x^3+3x e g (x) =4x. Há duas regiões sombreadas entre os gráficos. A primeira região é delimitada acima por f (x) e abaixo por g (x). A segunda região é delimitada acima por g (x), abaixo por f (x).

    \(\dfrac{1}{2}\, \text{units}^2\)

    Para os exercícios 20 a 25, faça um gráfico das equações e sombreie a área da região entre as curvas. Determine sua área integrando-a sobre o\(y\) eixo y.

    20)\(x=y^3\) e\( x = 3y−2\)

    21)\(x=y\) e\( x=y^3−y\)

    Responda

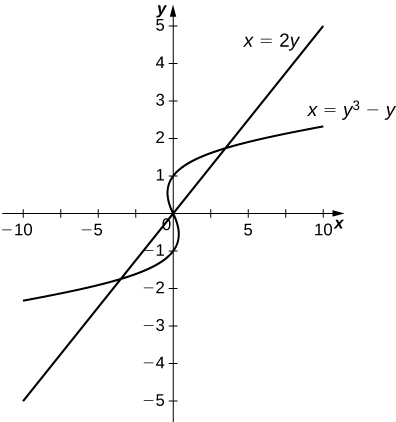
    Esta figura tem dois gráficos. Elas são as equações x=2y e x=y^3-y. Os gráficos se cruzam no terceiro quadrante e novamente no primeiro quadrante formando duas regiões fechadas entre eles.

    \(\dfrac{9}{2}\, \text{units}^2\)

    22)\(x=−3+y^2\) e\( x=y−y^2\)

    23)\(y^2=x\) e\(x=y+2\)

    Responda

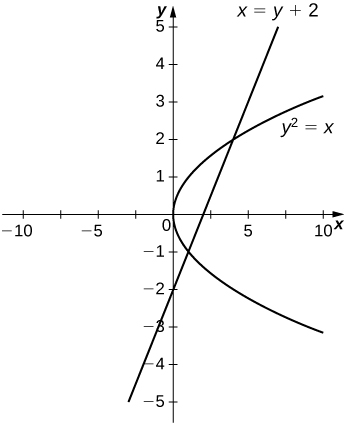
    Esta figura tem dois gráficos. São as equações x=y+2 e y^2=x. Os gráficos se cruzam, formando uma região entre eles

    \(\dfrac{9}{2}\, \text{units}^2\)

    24)\(x=|y|\) e\(2x=−y^2+2\)

    25)\(x=\sin y,\quad x=\cos(2y),\quad y=π/2\) e\( y=−π/2\)

    Responda

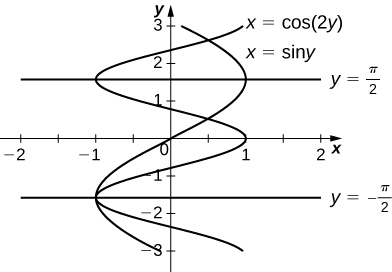
    Esta figura tem dois gráficos. Elas são as equações x=cos (y) e x=sin (y). Os gráficos se cruzam, formando duas regiões delimitadas acima pela linha y=pi/2 e abaixo pela linha y=-pi/2.

    \(\dfrac{3\sqrt{3}}{2}\, \text{units}^2\)

    Para os exercícios 26 a 37, faça um gráfico das equações e sombreie a área da região entre as curvas. Determine sua área integrando o\(x\) eixo -ou o\(y\) eixo -, o que parecer mais conveniente.

    26)\(x=y^4\) e\(x=y^5\)

    27)\(y=xe^x,\quad y=e^x,\quad x=0\),\(x=1\) e.

    Responda

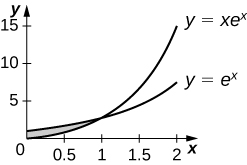
    Esta figura tem dois gráficos. Elas são as equações y=xe^x e y=e^x. Os gráficos se cruzam, formando uma região entre eles no primeiro quadrante.

    \(e^{−2}\, \text{units}^2\)

    28)\(y=x^6\) e\(y=x^4\)

    29)\(x=y^3+2y^2+1\) e\(x=−y^2+1\)

    Responda

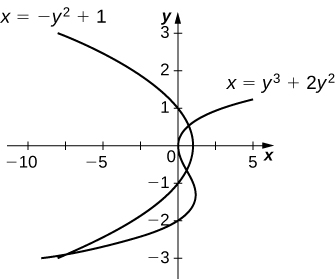
    Esta figura tem dois gráficos. Elas são as equações x=-y^2+1 e x=y^3+2y^2. Os gráficos se cruzam, formando duas regiões entre eles.

    \(\dfrac{27}{4}\, \text{units}^2\)

    30)\( y=|x|\) e\( y=x^2−1\)

    31)\(y=4−3x\) e\(y=\dfrac{1}{x}\)

    Responda

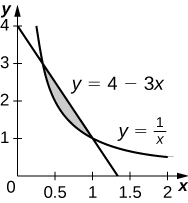
    Esta figura tem dois gráficos. São as equações y=4-3x e y=1/x. Os gráficos se cruzam, tendo a região entre eles sombreada. A região está no primeiro quadrante.

    \(\left(\dfrac{4}{3}−\ln(3)\right)\, \text{units}^2\)

    32)\(y=\sin x,\quad x=−π/6,\quad x=π/6,\) e\(y=\cos^3 x\)

    33)\(y=x^2−3x+2\) e\( y=x^3−2x^2−x+2\)

    Responda
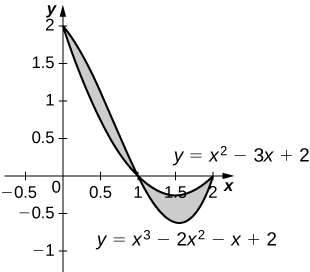
    Esta figura tem dois gráficos. Elas são as equações y=x^2-3x+2 e y=x^3-2x^2-x+2. Os gráficos se cruzam, tendo a região entre eles sombreada.
    \(\dfrac{1}{2}\)    unidades quadradas

    34)\(y=2\cos^3(3x),\quad y=−1,\quad x=\dfrac{π}{4},\) and \( x=−\dfrac{π}{4}\)

    (35)\(y+y^3=x\) and \(2y=x\)

    Responda

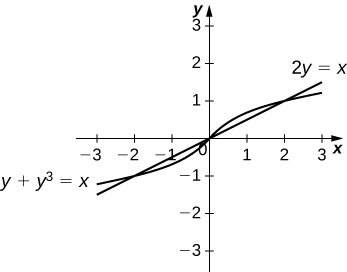
    Esta figura tem dois gráficos. Elas são as equações 2y=x e y+y^3=x. Os gráficos se cruzam, formando duas regiões. As regiões estão sombreadas.

    \(\dfrac{1}{2}\)unidades quadradas

    36)\( y=\sqrt{1−x^2}\) e\(y=x^2−1\)

    37)\(y=\cos^{−1}x,\quad y=\sin^{−1}x,\quad x=−1,\) e\( x=1\)

    Responda

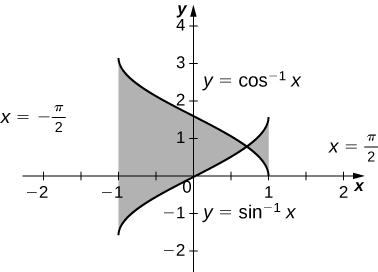
    Esta figura tem dois gráficos. Elas são as equações y=arccos (x) e y=arcsin (x). Os gráficos se cruzam, formando duas regiões. A primeira região é delimitada à esquerda por x=-1. A segunda região é limitada à direita por x=1. Ambas as regiões estão sombreadas.

    \(−2(\sqrt{2}−π)\)unidades quadradas

    Para os exercícios 38 a 47, encontre a área exata da região delimitada pelas equações dadas, se possível. Se você não conseguir determinar os pontos de interseção analiticamente, use uma calculadora para aproximar os pontos de interseção com três casas decimais e determinar a área aproximada da região.

    38) [T]\(x=e^y\) e\(y=x−2\)

    39) [T]\(y=x^2\) e\(y=\sqrt{1−x^2}\)

    Responda
    \(1.067\)unidades quadradas

    40) [T]\(y=3x^2+8x+9\) e\(3y=x+24\)

    41) [T]\(x=\sqrt{4−y^2}\) e\( y^2=1+x^2\)

    Responda
    \(0.852\)unidades quadradas

    42) [T]\(x^2=y^3\) e\(x=3y\)

    43) [T]\(y=\sin^3x+2,\quad y=\tan x,\quad x=−1.5,\) e\(x=1.5\)

    Responda
    \(7.523\)unidades quadradas

    44) [T]\(y=\sqrt{1−x^2}\) e\(y^2=x^2\)

    45) [T]\(y=\sqrt{1−x^2}\) e\(y=x^2+2x+1\)

    Responda
    \(\dfrac{3π−4}{12}\)unidades quadradas

    46) [T]\(x=4−y^2\) e\( x=1+3y+y^2\)

    47) [T]\(y=\cos x,\quad y=e^x,\quad x=−π,\quad\) e\(\quad x=0\)

    Responda
    \(1.429\)unidades quadradas

    48) O maior triângulo com uma base no\(x\) eixo -que se encaixa dentro da metade superior do círculo unitário\(y^2+x^2=1\) é dado por\( y=1+x\)\( y=1−x\) e. Veja a figura a seguir. Qual é a área dentro do semicírculo, mas fora do triângulo?

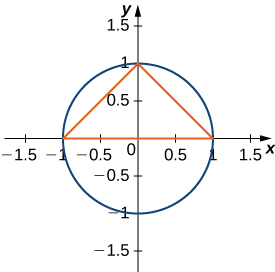
    Esta figura tem o gráfico de um círculo com centro na origem e raio de 1. Há um triângulo inscrito com base no eixo x de -1 a 1 e o terceiro canto no ponto y=1.

    49) Uma fábrica que vende telefones celulares tem uma função de custo marginal\(C(x)=0.01x^2−3x+229\), onde\(x\) representa o número de telefones celulares, e uma função de receita marginal dada por\(R(x)=429−2x.\) Encontre a área entre os gráficos dessas curvas e\(x=0.\) O que essa área representa?

    Responda
    Lucro total de $33.333,33 para 200 celulares vendidos

    50) Um parque de diversões tem uma função de custo marginal\(C(x)=1000e−x+5\), onde\(x\) representa o número de ingressos vendidos, e uma função de receita marginal dada por\(R(x)=60−0.1x\). Encontre o lucro total gerado ao vender\(550\) ingressos. Use uma calculadora para determinar os pontos de interseção, se necessário, com duas casas decimais.

    51) A tartaruga versus a lebre: A velocidade da lebre é dada pela função senoidal,\(H(t)=1−\cos((πt)/2)\) enquanto a velocidade da tartaruga é\(T(t)=(1/2)\tan^{−1}(t/4)\), onde o tempo\(t\) é medido em horas e a velocidade é medida em milhas por hora. Encontre a área entre as curvas de vez em quando\(t=0\) até a primeira vez após uma hora, quando a tartaruga e a lebre estão viajando na mesma velocidade. O que isso representa? Use uma calculadora para determinar os pontos de interseção, se necessário, com precisão de três casas decimais.

    Responda
    \(3.263\)mi representa a distância entre a lebre e a tartaruga

    52) A tartaruga versus a lebre: A velocidade da lebre é dada pela função senoidal,\(H(t)=(1/2)−(1/2)\cos(2πt)\) enquanto a velocidade da tartaruga é\(T(t)=\sqrt{t}\), onde o tempo\(t\) é medido em horas e a velocidade é medida em quilômetros por hora. Se a corrida terminar em 1 hora, quem venceu a corrida e por quanto? Use uma calculadora para determinar os pontos de interseção, se necessário, com precisão de três casas decimais.

    Para os exercícios 53 a 55, encontre a área entre as curvas integrando em relação a\(x\) e depois em relação\(y\) a. Um método é mais fácil do que o outro? Você obtém a mesma resposta?

    53)\(y=x^2+2x+1\) e\(y=−x^2−3x+4\)

    Responda
    \(\dfrac{343}{24}\)unidades quadradas

    54)\(y=x^4\) e\(x=y^5\)

    55)\(x=y^2−2\) e\(x=2y\)

    Responda
    \(4\sqrt{3}\)unidades quadradas

    Para os exercícios 56 a 57, resolva usando cálculo e, em seguida, verifique sua resposta com geometria.

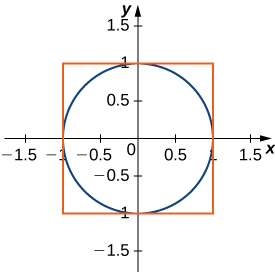
    56) Determine as equações para os lados do quadrado que toca o círculo unitário nos quatro lados, conforme visto na figura a seguir. Encontre a área entre o perímetro desse quadrado e o círculo unitário. Existe outra maneira de resolver isso sem usar o cálculo?

    Esta figura é o gráfico de um círculo centrado na origem com raio de 1. Há um quadrado circunscrito ao redor do círculo.

    57) Encontre a área entre o perímetro do círculo unitário e o triângulo criado a partir de\(y=2x+1,\,y=1−2x\) e\(y=−\dfrac{3}{5}\), como visto na figura a seguir. Existe uma maneira de resolver isso sem usar o cálculo?

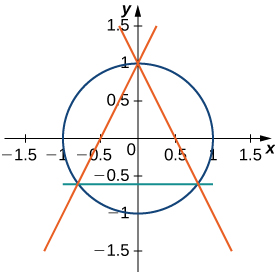
    Esta figura é o gráfico de um círculo centrado na origem com raio de 1. Há três linhas que cruzam o círculo. As linhas cruzam o círculo em três pontos para formar um triângulo dentro do círculo.

    Responda
    \( \left(π−\dfrac{32}{25}\right)\)unidades quadradas