6.1: Áreas entre curvas

Last updated
Save as PDF

Page ID: 187886

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Determine a área de uma região entre duas curvas por meio da integração com relação à variável independente.
Encontre a área de uma região composta.
Determine a área de uma região entre duas curvas por meio da integração com relação à variável dependente.

Em Introdução à Integração, desenvolvemos o conceito da integral definida para calcular a área abaixo de uma curva em um determinado intervalo. Nesta seção, expandimos essa ideia para calcular a área de regiões mais complexas. Começamos encontrando a área entre duas curvas que são funções de$\displaystyle x$, começando com o caso simples em que um valor de função é sempre maior que o outro. Em seguida, examinamos os casos em que os gráficos das funções se cruzam. Por fim, consideramos como calcular a área entre duas curvas que são funções de$\displaystyle y$.

Área de uma região entre duas curvas

Seja$\displaystyle f(x)$ e$\displaystyle g(x)$ seja funções contínuas em um intervalo$\displaystyle [a,b]$ como$\displaystyle f(x)≥g(x)$ ativado$\displaystyle [a,b]$. Queremos encontrar a área entre os gráficos das funções, conforme mostrado na Figura$\PageIndex{1}$.

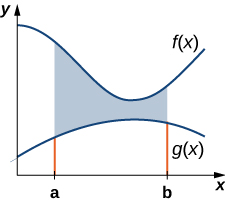
Esta figura é um gráfico no primeiro quadrante. Há duas curvas no gráfico. A curva mais alta é rotulada como “f (x)” e a curva inferior é rotulada como “g (x)”. Há dois limites no eixo x denominados a e b. Há uma área sombreada entre as duas curvas delimitada por linhas em x=a e x=b. — Figura$\PageIndex{1}$: A área entre os gráficos de duas funções$\displaystyle f(x)$ e$\displaystyle g(x)$, no intervalo$\displaystyle [a,b]$

Como fizemos antes, vamos particionar o intervalo no eixo x e aproximar a área entre os gráficos das funções com retângulos. Então, para$\displaystyle i=0,1,2,…,n$,$\displaystyle P={x_i}$ seja uma partição regular de$\displaystyle [a,b]$. Em seguida, para$\displaystyle i=1,2,…,n,$ escolher um ponto e$\displaystyle x^∗_i∈[x_{i−1},x_i]$, em cada intervalo,$\displaystyle [x_{i−1},x_i]$ construa um retângulo que se estende verticalmente de$\displaystyle g(x^∗_i)$ até$\displaystyle f(x^∗_i)$. A figura$\PageIndex{2a}$ mostra os retângulos quando$\displaystyle x^∗_i$ é selecionado para ser o ponto final esquerdo do intervalo$\displaystyle n=10$ e. A figura$\PageIndex{2b}$ mostra um retângulo representativo em detalhes.

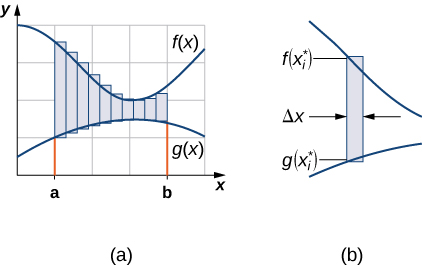
Essa figura tem três gráficos. O primeiro gráfico tem duas curvas, uma sobre a outra. Entre as curvas há um retângulo. A parte superior do retângulo está na curva superior chamada “f (x*)” e a parte inferior do retângulo está na curva inferior e rotulada como “g (x*)”. O segundo gráfico, denominado “(a)”, tem duas curvas no gráfico. A curva mais alta é rotulada como “f (x)” e a curva inferior é rotulada como “g (x)”. Há dois limites no eixo x rotulados a e b. Há uma área sombreada entre as duas curvas delimitada por linhas em x=a e x=b. O terceiro gráfico, denominado “(b)”, tem duas curvas uma sobre a outra. A primeira curva é rotulada como “f (x*)” e a curva inferior é rotulada como “g (x*)”. Há um retângulo sombreado entre os dois. A largura do retângulo é rotulada como “delta x”. — Figura$\PageIndex{2}$: (a) Podemos aproximar a área entre os gráficos de duas funções$\displaystyle f(x)$ e$\displaystyle g(x)$, com retângulos. (b) A área de um retângulo típico vai de uma curva para a outra.

A altura de cada retângulo individual é$\displaystyle f(x^∗_i)−g(x^∗_i)$ e a largura de cada retângulo é$\displaystyle Δx$. Somando as áreas de todos os retângulos, vemos que a área entre as curvas é aproximada por

\[\displaystyle A≈\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx. \nonumber \]

Esta é uma soma de Riemann, então tomamos o limite como$\displaystyle n→∞$ e obtemos

\[\displaystyle A=\lim_{n→∞}\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Essas descobertas estão resumidas no seguinte teorema.

Encontrando a área entre duas curvas

Seja$\displaystyle f(x)$ e$\displaystyle g(x)$ seja funções contínuas de tal forma que$\displaystyle f(x)≥g(x)$ ao longo de um intervalo [$\displaystyle a,b]$. Seja R denotar a região delimitada acima pelo gráfico de$\displaystyle f(x)$, abaixo pelo gráfico de$\displaystyle g(x)$, e à esquerda e à direita pelas linhas$\displaystyle x=a$ e$\displaystyle x=b$, respectivamente. Então, a área de$\textbf{R}$ é dada por

\[A=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Nós aplicamos esse teorema no exemplo a seguir.

Exemplo$\PageIndex{1}$: Finding the Area of a Region between Two Curves I

Se$\textbf{R}$ for a região delimitada acima pelo gráfico da função$\displaystyle f(x)=x+4$ e abaixo pelo gráfico da função no$\displaystyle g(x)=3−\dfrac{x}{2}$ intervalo$\displaystyle [1,4]$, encontre a área da região$\textbf{R}$.

Solução

A região é mostrada na figura a seguir.

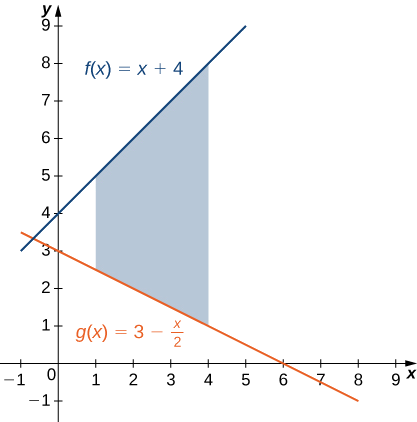
Esta figura tem dois gráficos lineares no primeiro quadrante. São as funções f (x) = x+4 e g (x) = 3-x/2. Entre essas linhas está uma região sombreada, delimitada acima por f (x) e abaixo por g (x). A área sombreada está entre x=1 e x=4. — Figura$\PageIndex{3}$: Uma região entre duas curvas é mostrada onde uma curva é sempre maior que a outra.

Nós temos

\[ \begin{align*} A =\int ^b_a[f(x)−g(x)]\,dx \\[4pt] =\int ^4_1[(x+4)−(3−\dfrac{x}{2})]\,dx=\int ^4_1\left[\dfrac{3x}{2}+1\right]\,dx \\[4pt] =[\dfrac{3x^2}{4}+x]\bigg|^4_1=(16−\dfrac{7}{4})=\dfrac{57}{4}. \end{align*}\]

A área da região é$\displaystyle \dfrac{57}{4}units^2$.

Exercício$\PageIndex{1}$

Se$\textbf{R}$ for a região delimitada pelos gráficos das funções$\displaystyle f(x)=\dfrac{x}{2}+5$ e$\displaystyle g(x)=x+\dfrac{1}{2}$ ao longo do intervalo$\displaystyle [1,5]$, encontre a área da região$\textbf{R}$.

Dica: Faça um gráfico das funções para determinar qual gráfico da função forma o limite superior e qual forma o limite inferior e, em seguida, siga o processo usado em Example.

Resposta: $\displaystyle 12$unidades ²

No exemplo$\PageIndex{1}$, definimos o intervalo de interesse como parte da declaração do problema. Muitas vezes, porém, queremos definir nosso intervalo de interesse com base em onde os gráficos das duas funções se cruzam. Isso é ilustrado no exemplo a seguir.

Exemplo$\PageIndex{2}$: Finding the Area of a Region between Two Curves II

Se$\textbf{R}$ for a região delimitada acima pelo gráfico da função$\displaystyle f(x)=9−(x/2)^2$ e abaixo pelo gráfico da função$\displaystyle g(x)=6−x$, encontre a área da região$\textbf{R}$.

Solução

A região é mostrada na figura a seguir.

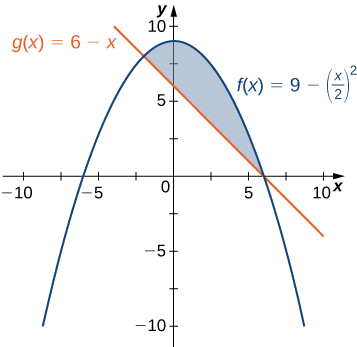
Esta figura tem dois gráficos no primeiro quadrante. São as funções f (x) = 9- (x/2) ^2 e g (x) = 6-x. Entre esses gráficos, uma parábola invertida e uma linha são uma região sombreada, delimitada acima por f (x) e abaixo por g (x). — Figura$\PageIndex{4}$: Este gráfico mostra a região abaixo do gráfico$\displaystyle f(x)$ e acima do gráfico de$\displaystyle g(x).$

Primeiro, precisamos calcular onde os gráficos das funções se cruzam. Configuração$\displaystyle f(x)=g(x),$ que obtemos

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 9−(\dfrac{x}{2})^2 =6−x\\[4pt] 9−\dfrac{x^2}{4} =6−x\\[4pt] 36−x^2 =24−4x\\[4pt] x^2−4x−12 =0\\[4pt] (x−6)(x+2) =0. \end{align*}\]

Os gráficos das funções se cruzam quando$\displaystyle x=6$ queremos integrar de$\displaystyle −2$ para$\displaystyle 6$.$\displaystyle x=−2,$ Uma vez que$\displaystyle f(x)≥g(x)$ para$\displaystyle −2≤x≤6,$ nós obtemos

\[\begin{align*} \displaystyle A =\int ^b_a[f(x)−g(x)]\,dx \\ =\int ^6_{−2} \left[9−(\dfrac{x}{2})^2−(6−x)\right]\,dx \\ =\int ^6_{−2}\left[3−\dfrac{x^2}{4}+x\right]\,dx \\ = \left. \left[3x−\dfrac{x^3}{12}+\dfrac{x^2}{2}\right] \right|^6_{−2}=\dfrac{64}{3}. \end{align*}\]

A área da região é de$\displaystyle 64/3$ unidades ².

Exercício$\PageIndex{2}$

Se$\textbf{R}$ for a região delimitada acima pelo gráfico da função$\displaystyle f(x)=x$ e abaixo pelo gráfico da função$\displaystyle g(x)=x^4$, encontre a área da região$\textbf{R}$.

Dica: Use o processo do Example$\PageIndex{2}$.

Resposta: $\displaystyle \dfrac{3}{10}$unidade ²

Áreas de regiões compostas

Até agora, exigimos$\displaystyle f(x)≥g(x)$ todo o intervalo de interesse, mas e se quisermos observar regiões delimitadas pelos gráficos de funções que se cruzam? Nesse caso, modificamos o processo que acabamos de desenvolver usando a função de valor absoluto.

Encontrando a área de uma região entre curvas que se cruzam

Deixe$\displaystyle f(x)$ e$\displaystyle g(x)$ seja funções contínuas ao longo de um intervalo$\displaystyle [a,b]$. Vamos$\textbf{R}$ denotar a região entre os gráficos de$\displaystyle f(x)$ e$\displaystyle g(x)$, e ser delimitada à esquerda e à direita pelas linhas$\displaystyle x=a$ e$\displaystyle x=b$, respectivamente. Então, a área de$\textbf{R}$ é dada por

\[A=\int ^b_a|f(x)−g(x)|dx. \nonumber \]

Na prática, a aplicação desse teorema exige que dividimos o intervalo$\displaystyle [a,b]$ e avaliemos várias integrais, dependendo de qual dos valores da função é maior em uma determinada parte do intervalo. Estudamos esse processo no exemplo a seguir.

Exemplo$\PageIndex{3}$: Finding the Area of a Region Bounded by Functions That Cross

Se$\textbf{R}$ for a região entre os gráficos das funções$\displaystyle f(x)=\sin x $ e$\displaystyle g(x)=\cos x$ ao longo do intervalo$\displaystyle [0,π]$, encontre a área da região$\textbf{R}$.

Solução

A região é mostrada na figura a seguir.

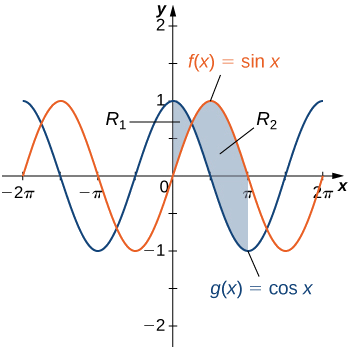
Esta figura tem dois gráficos. Elas são as funções f (x) = sinx e g (x) = cosx. Ambas são funções periódicas que lembram ondas. Há duas áreas sombreadas entre os gráficos. A primeira área sombreada é chamada de “R1” e tem g (x) acima de f (x). Essa região começa no eixo y e para onde as curvas se cruzam. A segunda região é chamada de “R2” e começa na interseção com f (x) acima de g (x). A região sombreada para em x=pi. — Figura$\PageIndex{5}$: A região entre duas curvas pode ser dividida em duas sub-regiões.

Os gráficos das funções se cruzam em$\displaystyle x=π/4$. Por$\displaystyle x∈[0,π/4], \cos x≥\sin x ,$ isso

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .$

Por outro lado, para$\displaystyle x∈[π/4,π], \sin x ≥\cos x,$ tanto

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.$

Então

\[ \begin{align*} A =\int ^b_a|f(x)−g(x)|dx \\[4pt] =\int ^π_0|\sin x −\cos x|dx=\int ^{π/4}_0(\cos x−\sin x )dx+\int ^{π}_{π/4}(\sin x −\cos x)dx \\[4pt] =[\sin x +\cos x]|^{π/4}_0+[−\cos x−\sin x ]|^π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

A área da região é de$\displaystyle 2\sqrt{2}$ unidades ^₂.

Exercício$\PageIndex{3}$

Se$\textbf{R}$ for a região entre os gráficos das funções$\displaystyle f(x)=\sin x $ e$\displaystyle g(x)=\cos x$ ao longo do intervalo$\displaystyle [π/2,2π]$, encontre a área da região$\textbf{R}$.

Dica: As duas curvas se cruzam em$\displaystyle x=(5π)/4.$

Resposta: $\displaystyle 2+2\sqrt{2}$unidades ²

Exemplo$\PageIndex{4}$: Finding the Area of a Complex Region

Considere a região mostrada na Figura$\PageIndex{6}$. Encontre a área de$\textbf{R}$.

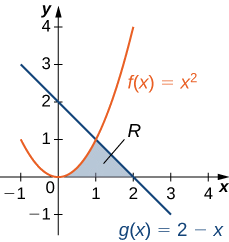
Esta figura tem dois gráficos no primeiro quadrante. Elas são as funções f (x) = x^2 e g (x) = 2-x. Entre esses gráficos está uma região sombreada, limitada à esquerda por f (x) e à direita por g (x). Tudo isso está acima do eixo x. A região é chamada R. A área sombreada está entre x=0 e x=2. — Figura$\PageIndex{6}$: Duas integrais são necessárias para calcular a área dessa região.

Solução

Como no exemplo$\PageIndex{3}$, precisamos dividir o intervalo em duas partes. Os gráficos das funções se cruzam em$\displaystyle x=1$ (definem$\displaystyle f(x)=g(x)$ e resolvem para x), então avaliamos duas integrais separadas: uma sobre o intervalo$\displaystyle [0,1]$ e outra sobre o intervalo$\displaystyle [1,2]$.

Ao longo do intervalo$\displaystyle [0,1]$, a região é limitada acima$\displaystyle f(x)=x^2$ e abaixo pelo eixo x, então temos

$\displaystyle A_1=\int ^1_0x^2dx=\dfrac{x^3}{3}∣^1_0=\dfrac{1}{3}.$

Ao longo$\displaystyle [1,2],$ do intervalo, a região é limitada acima$\displaystyle g(x)=2−x$ e abaixo pelo eixo x, então temos

$\displaystyle A_2=\int ^2_1(2−x)dx=[2x−\dfrac{x^2}{2}]∣^2_1=\dfrac{1}{2}.$

Somando essas áreas, obtemos

$\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.$

A área da região é de$\displaystyle 5/6$ unidades ²^.

Exercício$\PageIndex{4}$

Considere a região mostrada na figura a seguir. Encontre a área de$\textbf{R}$.

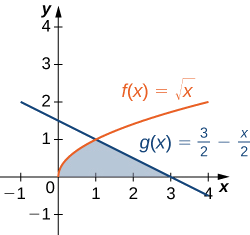
$Esta figura tem dois gráficos no primeiro quadrante. Elas são as funções f (x) = raiz quadrada de x e g (x) = 3/2 — x/2. Entre esses gráficos está uma região sombreada, limitada à esquerda por f (x) e à direita por g (x). Tudo isso está acima do eixo x. A área sombreada está entre x=0 e x=3.$

Dica: As duas curvas se cruzam em x=1

Resposta: $\displaystyle \dfrac{5}{3}$unidades ²

Regiões definidas em relação a y

No exemplo$\PageIndex{4}$, tivemos que avaliar duas integrais separadas para calcular a área da região. No entanto, há outra abordagem que requer apenas uma integral. E se tratarmos as curvas como funções de$\displaystyle y$, em vez de como funções de$\displaystyle x$? Figura de revisão. Observe que o gráfico à esquerda, mostrado em vermelho, é representado pela função$\displaystyle y=f(x)=x^2$. Poderíamos facilmente resolver isso para x e representar a curva pela função$\displaystyle x=v(y)=\sqrt{y}$. (Observe que também$\displaystyle x=−\sqrt{y}$ é uma representação válida da função$\displaystyle y=f(x)=x^2$ como uma função de$\displaystyle y$. No entanto, com base no gráfico, fica claro que estamos interessados na raiz quadrada positiva.) Da mesma forma, o gráfico certo é representado pela função$\displaystyle y=g(x)=2−x$, mas poderia ser facilmente representado pela função$\displaystyle x=u(y)=2−y$. Quando os gráficos são representados como funções de$\displaystyle y$, vemos que a região é limitada à esquerda pelo gráfico de uma função e à direita pelo gráfico da outra função. Portanto, se nos integrarmos em relação a$\displaystyle y$, precisamos avaliar apenas uma integral. Vamos desenvolver uma fórmula para esse tipo de integração.

Seja$\displaystyle u(y)$ e$\displaystyle v(y)$ seja funções contínuas em um intervalo$\displaystyle [c,d]$ tal que$\displaystyle u(y)≥v(y)$ para todos$\displaystyle y∈[c,d]$. Queremos encontrar a área entre os gráficos das funções, conforme mostrado na Figura$\PageIndex{7}$.

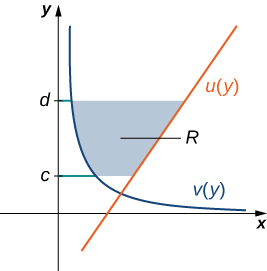
Esta figura tem dois gráficos no primeiro quadrante. Elas são as funções v (y) e u (y). Entre esses gráficos está uma região sombreada, limitada à esquerda por v (y) e à direita por u (y). A região é chamada de R. A área sombreada está entre os limites horizontais de y=c e y=d. — Figura$\PageIndex{7}$: Podemos encontrar a área entre os gráficos de duas funções,$\displaystyle u(y)$$\displaystyle v(y)$ e.

Desta vez, vamos dividir o intervalo no eixo y e usar retângulos horizontais para aproximar a área entre as funções. Então, para$\displaystyle i=0,1,2,…,n$,$\displaystyle Q={y_i}$ seja uma partição regular de$\displaystyle [c,d]$. Em seguida, para$\displaystyle i=1,2,…,n$, escolha um ponto e$\displaystyle y^∗_i∈[y_{i−1},y_i]$, em seguida, em cada intervalo,$\displaystyle [y_{i−1},y_i]$ construa um retângulo que se estende horizontalmente de$\displaystyle v(y^0∗_i)$ até$\displaystyle u(y^∗_i)$. A figura$\PageIndex{8a}$ mostra os retângulos quando$\displaystyle y^∗_i$ é selecionado para ser o ponto final inferior do intervalo$\displaystyle n=10$ e. A figura$\PageIndex{8b}$ mostra um retângulo representativo em detalhes.

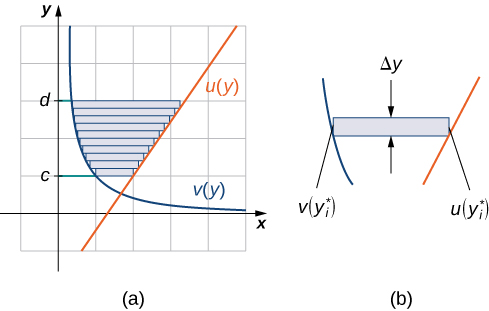
Esta figura tem três gráficos. A primeira figura tem duas curvas. São as funções v (y*) e u (y*). Entre essas curvas está um retângulo horizontal. A segunda figura chamada “(a)” é uma região sombreada, limitada à esquerda por v (y) e à direita por u (y). A área sombreada está entre os limites horizontais de y=c e y=d. Essa área sombreada é dividida em retângulos entre as curvas. A terceira figura, chamada “(b)”, são as duas curvas v (y*) e u (y*). Entre as curvas está um retângulo horizontal com largura delta y. — Figura$\PageIndex{8}$: (a) Aproximando a área entre os gráficos de duas funções$\displaystyle u(y)$ e$\displaystyle v(y)$, com retângulos. (b) A área de um retângulo típico.

A altura de cada retângulo individual é$\displaystyle Δy$ e a largura de cada retângulo é$\displaystyle u(y^∗_i)−v(y^∗_i)$. Portanto, a área entre as curvas é de aproximadamente

\[ A≈\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy . \nonumber \]

Esta é uma soma de Riemann, então consideramos o limite como$\displaystyle n→∞,$ obtenção

\[ \begin{align*} A =\lim_{n→∞}\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy \\[4pt] =\int ^d_c[u(y)−v(y)]dy. \end{align*}\]

Essas descobertas estão resumidas no seguinte teorema.

Encontrando a área entre duas curvas, integrando ao longo do eixo y

Seja$\displaystyle u(y)$ e$\displaystyle v(y)$ seja funções contínuas de tal forma que$\displaystyle u(y)≥v(y) $ para todos$\displaystyle y∈[c,d]$. Vamos$\textbf{R}$ indicar a região delimitada à direita pelo gráfico de$\displaystyle u(y)$, à esquerda pelo gráfico de$\displaystyle v(y)$, e acima e abaixo pelas linhas$\displaystyle y=d$ e$\displaystyle y=c$, respectivamente. Então, a área de$\textbf{R}$ é dada por

\[A=\int ^d_c[u(y)−v(y)]dy. \nonumber \]

Exemplo$\PageIndex{5}$: Integrating with Respect to y

Vamos revisitar o Exemplo$\PageIndex{4}$, só que desta vez vamos nos integrar com relação$\displaystyle y$ a. $\textbf{R}$Seja a região representada na Figura$\PageIndex{9}$. Encontre a área de$\textbf{R}$ integrando em relação$\displaystyle y$ a.

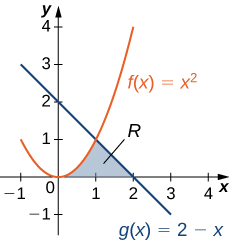
Solução

Devemos primeiro expressar os gráficos como funções de$\displaystyle y$. Como vimos no início desta seção, a curva à esquerda pode ser representada pela função$\displaystyle x=v(y)=\sqrt{y}$ e a curva à direita pode ser representada pela função$\displaystyle x=u(y)=2−y$.

Agora temos que determinar os limites da integração. A região é delimitada abaixo pelo eixo x, então o limite inferior de integração é$\displaystyle y=0$. O limite superior de integração é determinado pelo ponto em que os dois gráficos se cruzam, que é o ponto$\displaystyle (1,1)$, então o limite superior de integração é$\displaystyle y=1$. Assim, nós temos$\displaystyle [c,d]=[0,1]$.

Calculando a área da região, obtemos

\[ \begin{align*} A =\int ^d_c[u(y)−v(y)]dy \\[4pt] =\int ^1_0[(2−y)−\sqrt{y}]dy\\[4pt] =[2y−\dfrac{y^2}{2}−\dfrac{2}{3}y^{3/2}]∣^1_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

A área da região é de$\displaystyle 5/6$ unidades ².

Exercício$\PageIndex{5}$

Vamos revisitar o ponto de verificação associado ao Example$\PageIndex{4}$, só que desta vez, vamos integrar com relação$\displaystyle y$ a. $\textbf{R}$Seja a região representada na figura a seguir. Encontre a área de$\textbf{R}$ integrando em relação$\displaystyle y$ a.

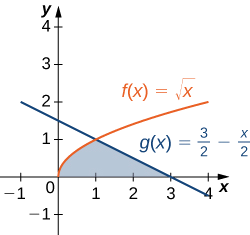
Dica: Siga o processo do exemplo anterior.

Resposta: $\displaystyle \dfrac{5}{3}$unidades ²

Conceitos chave

Assim como integrais definidas podem ser usadas para encontrar a área sob uma curva, elas também podem ser usadas para encontrar a área entre duas curvas.
Para encontrar a área entre duas curvas definidas por funções, integre a diferença das funções.
Se os gráficos das funções se cruzarem ou se a região for complexa, use o valor absoluto da diferença das funções. Nesse caso, pode ser necessário avaliar duas ou mais integrais e adicionar os resultados para encontrar a área da região.
Às vezes, pode ser mais fácil integrar com relação a y para encontrar a área. Os princípios são os mesmos, independentemente de qual variável é usada como variável de integração.

Equações chave

Área entre duas curvas, integrando no eixo x

$\displaystyle A=\int ^b_a[f(x)−g(x)]dx$

Área entre duas curvas, integrando no eixo y

$\displaystyle A=\int ^d_c[u(y)−v(y)]dy$

Encontrando a área entre duas curvas

Exemplo\(\PageIndex{1}\): Finding the Area of a Region between Two Curves I

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Finding the Area of a Region between Two Curves II

Exercício\(\PageIndex{2}\)

Encontrando a área de uma região entre curvas que se cruzam

Exemplo\(\PageIndex{3}\): Finding the Area of a Region Bounded by Functions That Cross

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): Finding the Area of a Complex Region

Exercício\(\PageIndex{4}\)

Encontrando a área entre duas curvas, integrando ao longo do eixo y

Exemplo\(\PageIndex{5}\): Integrating with Respect to y

Exercício\(\PageIndex{5}\)