6.3: Volumes de revolução - Conchas cilíndricas

Last updated
Save as PDF

Page ID: 187839

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Calcule o volume de um sólido de revolução usando o método de conchas cilíndricas.
Compare os diferentes métodos para calcular um volume de revolução.

Nesta seção, examinamos o método das conchas cilíndricas, o método final para encontrar o volume de um sólido de revolução. Podemos usar esse método nos mesmos tipos de sólidos que o método de disco ou o método de lavagem; no entanto, com os métodos de disco e lavadora, nos integramos ao longo do eixo de coordenadas paralelo ao eixo de revolução. Com o método das conchas cilíndricas, nós nos integramos ao longo do eixo coordenado perpendicular ao eixo de revolução. A capacidade de escolher qual variável de integração queremos usar pode ser uma vantagem significativa com funções mais complicadas. Além disso, a geometria específica do sólido às vezes torna o método de usar conchas cilíndricas mais atraente do que o método de lavagem. Na última parte desta seção, analisamos todos os métodos para encontrar volume que estudamos e apresentamos algumas diretrizes para ajudá-lo a determinar qual método usar em uma determinada situação.

O método das conchas cilíndricas

Novamente, estamos trabalhando com uma sólida revolução. Como antes, definimos uma região$R$, limitada acima pelo gráfico de uma função$y=f(x)$, abaixo pelo $x$eixo -e à esquerda e à direita pelas linhas$x=a$ e$x=b$, respectivamente, conforme mostrado na Figura$\PageIndex{1a}$. Em seguida, giramos essa região em torno do$y$ eixo -, conforme mostrado na Figura$\PageIndex{1b}$. Observe que isso é diferente do que fizemos antes. Anteriormente, regiões definidas em termos de funções de$x$ eram giradas em torno do $x$eixo -ou de uma linha paralela a ele.

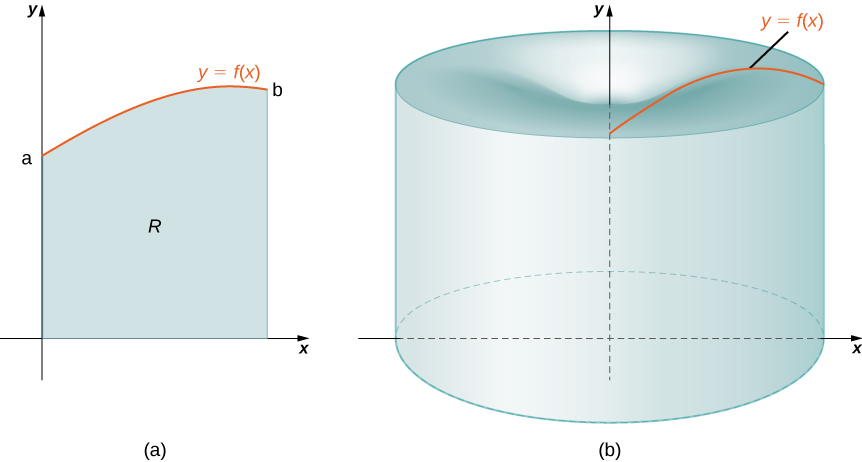
Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e é uma curva crescente no primeiro quadrante. A curva é rotulada como “y=f (x)”. A curva começa no eixo y em y=a. Abaixo da curva, acima do eixo x há uma região sombreada chamada “R”. A região sombreada é delimitada à direita pela linha x=b. O segundo gráfico é um sólido tridimensional. Ele foi criado girando a região sombreada de “a” em torno do eixo y. — Figura$\PageIndex{1}$: (a) Uma região delimitada pelo gráfico de uma função de$x$. (b) O sólido da revolução formado quando a região é girada em torno do **$y$eixo.**

Como fizemos várias vezes antes, particione o intervalo$[a,b]$ usando uma partição normal$P={x_0,x_1,…,x_n}$ e, para$i=1,2,…,n$, escolha um ponto$x^∗_i∈[x_{i−1},x_i]$. Em seguida, construa um retângulo sobre o intervalo$[x_{i−1},x_i]$ de altura$f(x^∗_i)$ e largura$Δx$. Um retângulo representativo é mostrado na Figura$\PageIndex{2a}$. Quando esse retângulo é girado em torno do$y$ eixo -, em vez de um disco ou uma arruela, obtemos uma concha cilíndrica, conforme mostrado na Figura$\PageIndex{2}$.

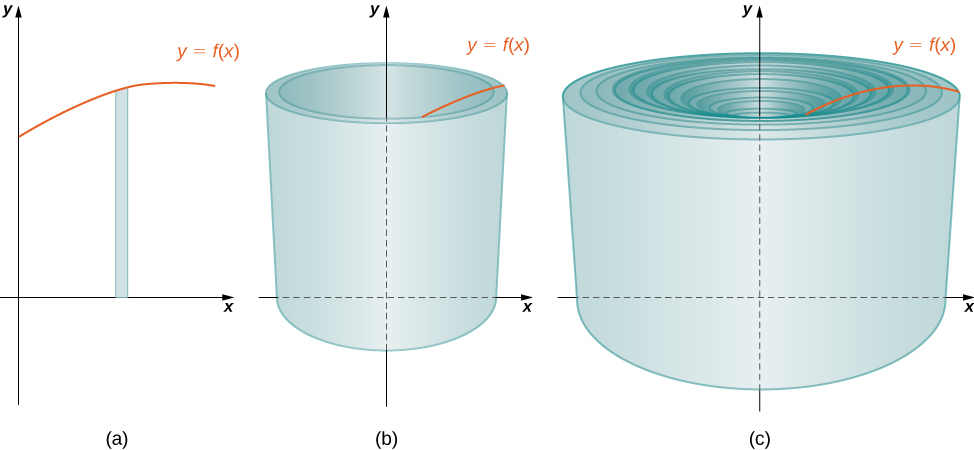
Esta figura tem duas imagens. A primeira é uma concha cilíndrica, oca no meio. Tem um eixo vertical no centro. Há também uma curva que encontra a parte superior do cilindro. A segunda imagem é um conjunto de cilindros concêntricos, um dentro do outro formando um agrupamento de cilindros. — Figura$\PageIndex{2}$: (a) Um retângulo representativo. (b) Quando esse retângulo é girado em torno do **$y$eixo -,** o resultado é uma concha cilíndrica. (c) Quando juntamos todas as conchas, obtemos uma aproximação do sólido original.

Para calcular o volume dessa concha, considere a Figura$\PageIndex{3}$.

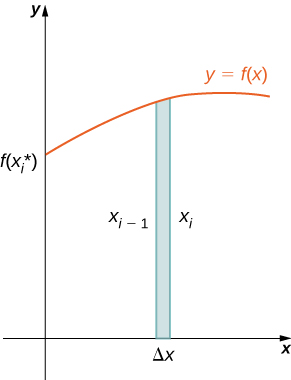
Esta figura é um gráfico no primeiro quadrante. A curva está aumentando e é rotulada como “y=f (x)”. A curva começa no eixo y em f (x*). Abaixo da curva, há um retângulo sombreado. O retângulo começa no eixo x. A largura do retângulo é delta x. Os dois lados do retângulo são identificados como “xsub (i-1)” e “xsubi”. — Figura$\PageIndex{3}$: Calculando o volume da casca.

O invólucro é um cilindro, então seu volume é a área da seção transversal multiplicada pela altura do cilindro. As seções transversais são anéis (regiões em forma de anel — essencialmente, círculos com um orifício no centro), com raio externo$x_i$ e raio interno$x_{i−1}$. Assim, a área da seção transversal é$πx^2_i−πx^2_{i−1}$. A altura do cilindro é$f(x^∗_i).$ Então o volume da casca é

\[ \begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_{i}−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}). \end{align*}\]

Observe que$x_i−x_{i−1}=Δx,$, portanto, temos

\[V_{shell}=2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)\,Δx. \nonumber \]

Além disso,$\dfrac {x_i+x_{i−1}}{2}$ é tanto o ponto médio do intervalo$[x_{i−1},x_i]$ quanto o raio médio da concha, e podemos aproximar isso em$x^∗_i$. Em seguida, temos

\[V_{shell}≈2π\,f(x^∗_i)x^∗_i\,Δx. \nonumber \]

Outra forma de pensar nisso é pensar em fazer um corte vertical na casca e depois abri-la para formar uma placa plana (Figura$\PageIndex{4}$).

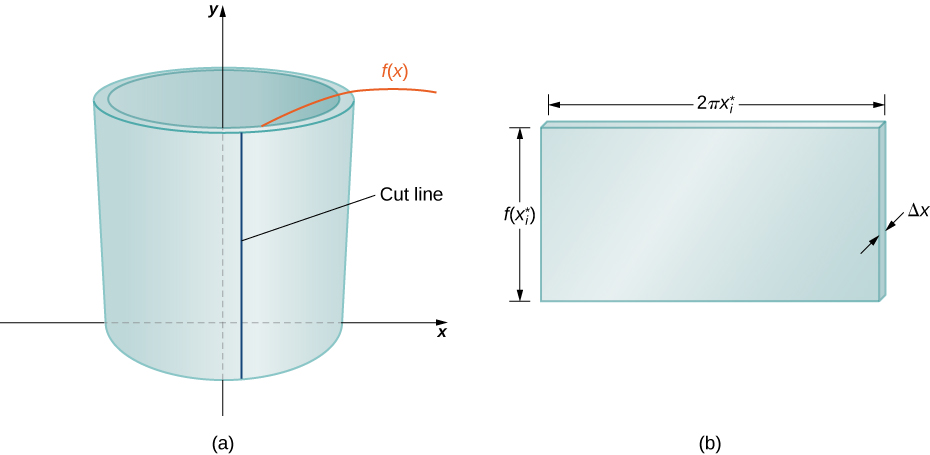
Esta figura tem duas imagens. O primeiro é rotulado como “a” e é de um cilindro oco ao redor do eixo y. Na frente deste cilindro há uma linha vertical chamada “linha de corte”. A altura do cilindro é “y=f (x)”. A segunda figura é rotulada como “b” e é um bloco retangular sombreado. A altura do retângulo é “f (x*), a largura do retângulo é “2pix*” e a espessura do retângulo é “delta x”. — Figura$\PageIndex{4}$: (a) Faça um corte vertical em uma concha representativa. (b) Abra o invólucro para formar uma placa plana.

Na realidade, o raio externo da casca é maior que o raio interno e, portanto, a borda traseira da placa seria um pouco maior que a borda frontal da placa. No entanto, podemos aproximar a casca achatada por uma placa plana de altura$f(x^∗_i)$$2πx^∗_i$, largura e espessura$Δx$ (Figura). O volume da casca, então, é aproximadamente o volume da placa plana. Multiplicando a altura, largura e profundidade da placa, obtemos

\[V_{shell}≈f(x^∗_i)(2π\,x^∗_i)\,Δx, \nonumber \]

que é a mesma fórmula que tínhamos antes.

Para calcular o volume de todo o sólido, adicionamos os volumes de todas as conchas e obtemos

\[V≈\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx). \nonumber \]

Aqui temos outra soma de Riemann, desta vez para a função$2π\,x\,f(x).$ Tomando o limite como nos$n→∞$ dá

\[V=\lim_{n→∞}\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx)=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Isso leva à seguinte regra para o método de conchas cilíndricas.

Regra: O método das conchas cilíndricas

$f(x)$Seja contínuo e não negativo. Defina$R$ como a região delimitada acima pelo gráfico de$f(x)$, abaixo pelo$x$ eixo$x=a$ -, à esquerda pela linha e à direita pela linha$x=b$. Então, o volume do sólido de revolução formado pela rotação$R$ em torno do$y$ eixo -é dado por

\[V=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Agora vamos considerar um exemplo.

Exemplo$\PageIndex{1}$: The Method of Cylindrical Shells I

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=1/x$ e abaixo pelo $x$eixo -ao longo do intervalo$[1,3]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno do$y$ eixo.

Solução

Primeiro, devemos representar graficamente a região$R$ e o sólido de revolução associado, conforme mostrado na Figura$\PageIndex{5}$.

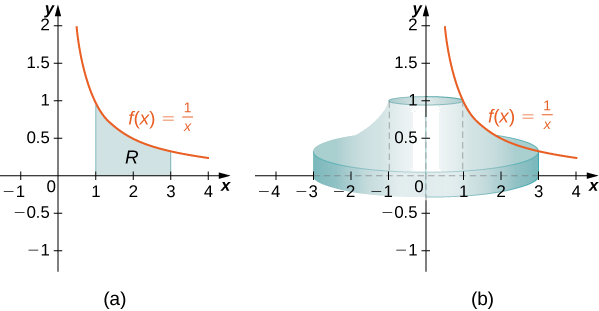
Esta figura tem três imagens. O primeiro é um sólido que foi formado pela rotação da curva y = 1/x em torno do eixo y. O sólido começa no eixo x e para onde y=1. A segunda imagem é rotulada como “a” e é o gráfico de y = 1/x no primeiro quadrante. Abaixo da curva está uma região sombreada chamada “R”. A região é limitada pela curva, o eixo x, à esquerda em x=1 e à direita em x=3. A terceira imagem é chamada de “b” e é metade do sólido formado pela rotação da região sombreada em torno do eixo y. — Figura$\PageIndex{5}$: (a) A região$R$ abaixo do gráfico do$f(x)=1/x$ intervalo$[1,3]$. (b) O sólido da revolução gerado pela rotação em$R$ torno do$y$ eixo.

Figura$\PageIndex{5}$ (c) Visualizando o sólido da revolução com Calcplot3d.

Em seguida, o volume do sólido é dado por

\[ \begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^3_1\left(2π\,x\left(\dfrac {1}{x}\right)\right)\,dx \\ =\int ^3_12π\,dx\\ =2π\,x\bigg|^3_1=4π\,\text{units}^3. \end{align*}\]

Exercício$\PageIndex{1}$

Defina R como a região delimitada acima pelo gráfico de$f(x)=x^2$ e abaixo pelo$x$ eixo -ao longo do intervalo$[1,2]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno do$y$ eixo.

Dica: Use o procedimento do Example$\PageIndex{1}$.

Responda: $\dfrac{15π}{2} \, \text{units}^3 $

Exemplo$\PageIndex{2}$: The Method of Cylindrical Shells II

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=2x−x^2$ e abaixo pelo$x$ eixo -ao longo do intervalo$[0,2]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno do $y$eixo.

Solução

Primeiro represente graficamente a região$R$ e o sólido de revolução associado, conforme mostrado na Figura$\PageIndex{6}$.

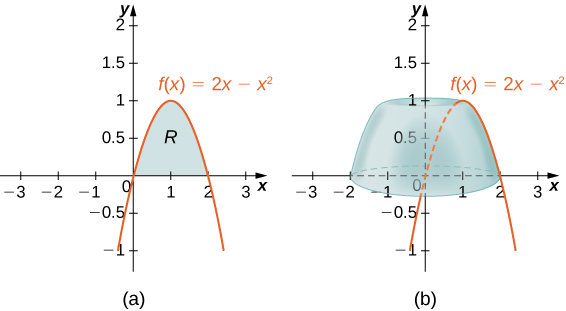
Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e é a curva f (x) =2x-x^2. É uma parábola invertida que cruza o eixo x na formiga de origem em x=2. Sob a curva, a região no primeiro quadrante está sombreada e é rotulada como “R”. A segunda figura é um gráfico da mesma curva. No gráfico há um sólido que é formado pela rotação da região de “a” em torno do eixo y. — Figura$\PageIndex{6}$: (a) A região$R$ *abaixo do gráfico do$f(x)=2x−x^2$* *intervalo$[0,2].$* *(b) O volume de revolução obtido pela rotação* $R$*sobre o$y$* *eixo -.*

Em seguida, o volume do sólido é dado por

\[\begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^2_0(2π\,x(2x−x^2))\,dx \\ = 2π\int ^2_0(2x^2−x^3)\,dx \\ =2π \left. \left[\dfrac {2x^3}{3}−\dfrac {x^4}{4}\right]\right|^2_0 \\ =\dfrac {8π}{3}\,\text{units}^3 \end{align*}\]

Exercício$\PageIndex{2}$

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=3x−x^2$ e abaixo pelo$x$ eixo -ao longo do intervalo$[0,2]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno do$y$ eixo.

Dica

Use o processo do Example$\PageIndex{2}$.

Responda

$8π \, \text{units}^3 $

Assim como o método de disco e o método de lavagem, podemos usar o método de conchas cilíndricas com sólidos de revolução, girados em torno do$x$ eixo -, quando queremos integrar em relação$y$ a. A regra análoga para esse tipo de sólido é dada aqui.

Regra: O método de conchas cilíndricas para sólidos de revolução em torno do$x$-axis

$g(y)$Seja contínuo e não negativo. Defina$Q$ como a região delimitada à direita pelo gráfico de$g(y)$, à esquerda pelo$y$ eixo -, abaixo pela linha$y=c$ e acima pela linha$y=d$. Então, o volume do sólido de revolução formado pela rotação$Q$ em torno do$x$ eixo -é dado por

\[V=\int ^d_c(2π\,y\,g(y))\,dy. \nonumber \]

Exemplo$\PageIndex{3}$: The Method of Cylindrical Shells for a Solid Revolved around the $x$-axis

Defina$Q$ como a região delimitada à direita pelo gráfico de$g(y)=2\sqrt{y}$ e à esquerda pelo$y$ eixo -para$y∈[0,4]$. Encontre o volume do sólido da revolução formado pela rotação$Q$ em torno do$x$ eixo.

Solução

Primeiro, precisamos representar graficamente a região$Q$ e o sólido de revolução associado, conforme mostrado na Figura$\PageIndex{7}$.

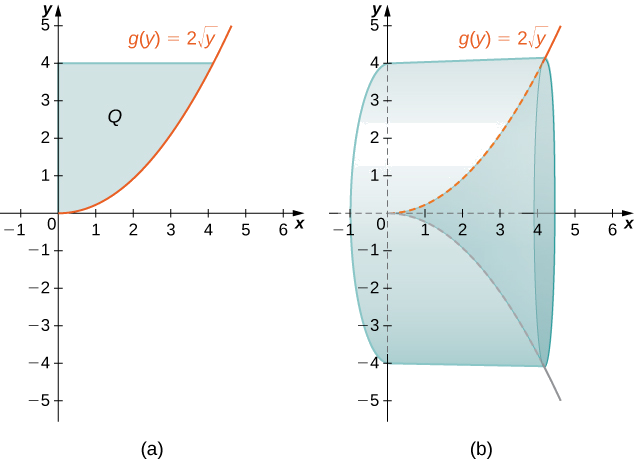
$Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e é a curva g (y) =2squareroot (y). É uma curva crescente no primeiro quadrante começando na origem. Entre o eixo y e a curva, há uma região sombreada chamada “Q”. A região sombreada é delimitada acima pela linha y=4. O segundo gráfico é a mesma curva em “a” e rotulada como “b”. Ele também tem uma região sólida que foi formada pela rotação da curva em “a” em torno do eixo x. O sólido começa no eixo y e para em x=4.$
Figura$\PageIndex{7}$: (a) A região$Q$ à esquerda da função$g(y)$ durante o intervalo$[0,4]$. (b) O sólido da revolução gerado pela rotação$Q$ em torno do$x$ eixo.

Identifique a região sombreada$Q$. Em seguida, o volume do sólido é dado por

\[ \begin{align*} V =\int ^d_c(2π\,y\,g(y))\,dy \\ =\int ^4_0(2π\,y(2\sqrt{y}))\,dy \\ =4π\int ^4_0y^{3/2}\,dy \\ =4π\left[\dfrac {2y^{5/2}}{5}\right]∣^4_0 \\ =\dfrac {256π}{5}\, \text{units}^3 \end{align*}\]

Exercício$\PageIndex{3}$

Defina$Q$ como a região delimitada à direita pelo gráfico de$g(y)=3/y$ e à esquerda pelo$y$ eixo -para$y∈[1,3]$. Encontre o volume do sólido da revolução formado pela rotação$Q$ em torno do$x$ eixo.

Dica

Use o processo do Example$\PageIndex{3}$.

Responda

$12π$unidades ³

Para o próximo exemplo, examinamos um sólido de revolução para o qual o gráfico de uma função é girado em torno de uma linha diferente de um dos dois eixos coordenados. Para configurar isso, precisamos revisitar o desenvolvimento do método das conchas cilíndricas. Lembre-se de que encontramos o volume de uma das conchas a ser dado por

\[\begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_i−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}).\end{align*}\]

Isso foi baseado em uma concha com um raio externo de$x_i$ e um raio interno de$x_{i−1}$. Se, no entanto, girarmos a região em torno de uma linha diferente do$y$ eixo -, teremos um raio externo e interno diferentes. Suponha, por exemplo, que rotacionemos a região em torno da linha$x=−k,$ onde$k$ há alguma constante positiva. Então, o raio externo da casca é$x_i+k$ e o raio interno da casca é$x_{i−1}+k$. Substituindo esses termos na expressão de volume, vemos que quando uma região plana é girada em torno da linha,$x=−k,$ o volume de uma concha é dado por

\[\begin{align*} V_{shell} =2π\,f(x^∗_i)(\dfrac {(x_i+k)+(x_{i−1}+k)}{2})((x_i+k)−(x_{i−1}+k)) \\[4pt] =2π\,f(x^∗_i)\left(\left(\dfrac {x_i+x_{i−2}}{2}\right)+k\right)Δx.\end{align*}\]

Como antes, notamos que$\dfrac {x_i+x_{i−1}}{2}$ é o ponto médio do intervalo$[x_{i−1},x_i]$ e pode ser aproximado por$x^∗_i$. Então, o volume aproximado da casca é

\[V_{shell}≈2π(x^∗_i+k)f(x^∗_i)Δx. \nonumber \]

O restante do desenvolvimento prossegue como antes, e vemos que

\[V=\int ^b_a(2π(x+k)f(x))dx. \nonumber \]

Também podemos girar a região em torno de outras linhas horizontais ou verticais, como uma linha vertical no meio plano direito. Em cada caso, a fórmula do volume deve ser ajustada de acordo. Especificamente, o$x$ termo -na integral deve ser substituído por uma expressão representando o raio de uma concha. Para ver como isso funciona, considere o exemplo a seguir.

Exemplo$\PageIndex{4}$: A Region of Revolution Revolved around a Line

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=x$ e abaixo pelo$x$ eixo -ao longo do intervalo$[1,2]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno da linha$x=−1.$

Solução

Primeiro, faça um gráfico da região$R$ e do sólido de revolução associado, conforme mostrado na Figura$\PageIndex{8}$.

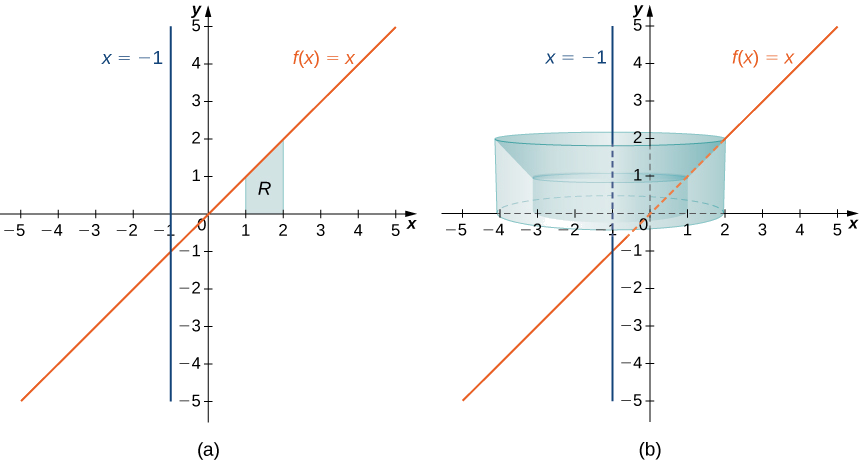
$Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e é a linha f (x) =x, uma linha diagonal que passa pela origem. Há uma região sombreada acima do eixo x abaixo da linha chamada “R”. Essa região é limitada à esquerda pela linha x=1 e à direita pela linha x=2. Há também a linha vertical x=-1 no gráfico. A segunda figura tem os mesmos gráficos de “a” e é rotulada como “b”. Também no gráfico está um sólido formado pela rotação da região “R” do primeiro gráfico em torno da linha x=-1.$
Figura$\PageIndex{8}$: (a) A região$R$ entre o gráfico de$f(x)$ e o$x$ eixo -ao longo do intervalo$[1,2]$. (b) O sólido da revolução gerado pela rotação$R$ em torno da linha$x=−1.$

Observe que o raio de uma concha é dado por$x+1$. Em seguida, o volume do sólido é dado por

\[\begin{align*} V =\int ^2_1 2π(x+1)f(x)\, dx \\ =\int ^2_1 2π(x+1)x \, dx=2π\int ^2_1 x^2+x \, dx \\ =2π \left[\dfrac{x^3}{3}+\dfrac{x^2}{2}\right]\bigg|^2_1 \\ =\dfrac{23π}{3} \, \text{units}^3 \end{align*}\]

Exercício$\PageIndex{4}$

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=x^2$ e abaixo pelo$x$ eixo -ao longo do intervalo$[0,1]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno da linha$x=−2$.

Dica

Use o processo do Example$\PageIndex{4}$.

Responda

$\dfrac {11π}{6}$unidades ³

Para nosso exemplo final nesta seção, vamos ver o volume de um sólido de revolução para o qual a região da revolução é delimitada pelos gráficos de duas funções.

Exemplo$\PageIndex{5}$: A Region of Revolution Bounded by the Graphs of Two Functions

Defina$R$ como a região delimitada acima pelo gráfico da função$f(x)=\sqrt{x}$ e abaixo pelo gráfico da função no$g(x)=1/x$ intervalo$[1,4]$. Encontre o volume do sólido de revolução gerado pela rotação$R$ em torno do$y$ eixo.

Solução

Primeiro, faça um gráfico da região$R$ e do sólido de revolução associado, conforme mostrado na Figura$\PageIndex{9}$.

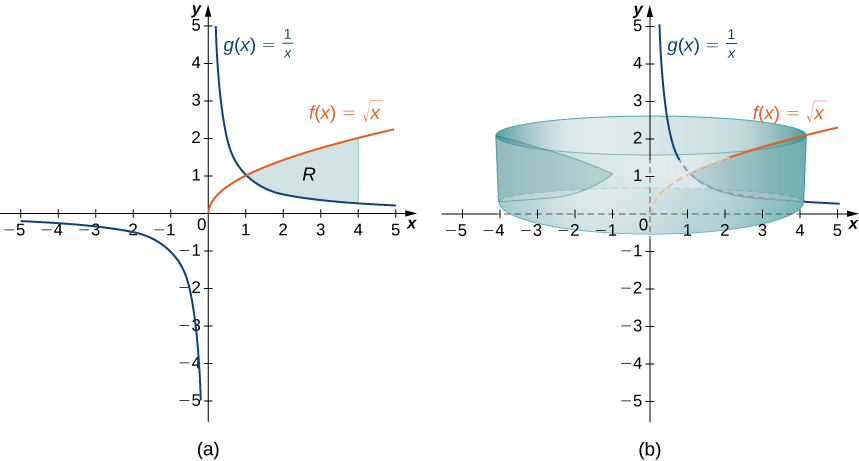
$Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e tem duas curvas. As curvas são os gráficos de f (x) =raiz quadrada (x) e g (x) =1/x. No primeiro quadrante, as curvas se cruzam em (1,1). Entre as curvas no primeiro quadrante, há uma região sombreada chamada “R”, limitada à direita pela linha x=4. O segundo gráfico é rotulado como “b” e é o mesmo que os gráficos em “a”. Também neste gráfico está um sólido que foi formado pela rotação da região “R” da figura “a” em torno do eixo y.$
Figura$\PageIndex{9}$: (a) A região$R$ entre o gráfico de$f(x)$ e o gráfico de$g(x)$ ao longo do intervalo$[1,4]$. (b) O sólido da revolução gerado pela rotação$R$ em torno do$y$ eixo.

Observe que o eixo de revolução é o$y$ eixo -, então o raio de uma concha é dado simplesmente por$x$. Não precisamos fazer nenhum ajuste no termo x do nosso integrando. A altura de uma concha, no entanto, é dada por$f(x)−g(x)$, então, neste caso, precisamos ajustar o$f(x)$ termo do integrando. Em seguida, o volume do sólido é dado por

\[\begin{align*} V =\int ^4_1(2π\,x(f(x)−g(x)))\,dx \\[4pt] = \int ^4_1(2π\,x(\sqrt{x}−\dfrac {1}{x}))\,dx=2π\int ^4_1(x^{3/2}−1)dx \\[4pt] = 2π\left[\dfrac {2x^{5/2}}{5}−x\right]\bigg|^4_1=\dfrac {94π}{5} \, \text{units}^3. \end{align*}\]

Exercício$\PageIndex{5}$

Defina$R$ como a região delimitada acima pelo gráfico de$f(x)=x$ e abaixo pelo gráfico do$g(x)=x^2$ intervalo$[0,1]$. Encontre o volume do sólido da revolução formado pela rotação$R$ em torno do$y$ eixo.

Dica

Dica: use o processo do Example$\PageIndex{5}$.

Responda

$\dfrac {π}{6}$unidades ³

Qual método devemos usar?

Estudamos vários métodos para encontrar o volume de um sólido de revolução, mas como sabemos qual método usar? Geralmente, tudo se resume a uma escolha de qual integral é mais fácil de avaliar. A figura$\PageIndex{10}$ descreve as diferentes abordagens para sólidos de revolução em torno do$x$ eixo y. Cabe a você desenvolver a tabela análoga para sólidos de revolução ao redor do$y$ eixo.

$Esta figura é uma tabela que compara os diferentes métodos para encontrar volumes de sólidos de revolução. As colunas na tabela são rotuladas como “comparação”, “método de disco”, “método de lavagem” e “método shell”. As linhas são rotuladas como “fórmula de volume”, “sólido”, “intervalo para partição”, “retângulos”, “região típica” e “retângulo”. Na coluna do método do disco, a fórmula é dada como a integral definida de a a b de pi vezes [f (x)] ^2. O sólido não tem cavidade no centro, a partição é [a, b], os retângulos são verticais e a região típica é uma região sombreada acima do eixo x e abaixo da curva de f (x). Na coluna do método de lavagem, a fórmula é dada como a integral definida de a a b de pi vezes [f (x)] ^2- [g (x)] ^2. O sólido tem uma cavidade no centro, a partição é [a, b], os retângulos são verticais e a região típica é uma região sombreada acima da curva de g (x) e abaixo da curva de f (x). Na coluna do método shell, a fórmula é dada como a integral definida de c a d de 2pi vezes yg (y). O sólido está com ou sem uma cavidade no centro, a partição é [c, d], os retângulos são horizontais e a região típica é uma região sombreada acima do eixo x e abaixo da curva de g (y).$
Figura$\PageIndex{10}$

Vamos dar uma olhada em alguns problemas adicionais e decidir a melhor abordagem a ser adotada para resolvê-los.

Exemplo$\PageIndex{6}$: Selecting the Best Method

Para cada um dos problemas a seguir, selecione o melhor método para encontrar o volume de um sólido de revolução gerado pela rotação da região dada em torno do$x$ eixo -e configure a integral para encontrar o volume (não avalie a integral).

A região delimitada pelos gráficos de$y=x, y=2−x,$ e pelo$x$ eixo -.

A região delimitada pelos gráficos de$y=4x−x^2$ e pelo$x$ eixo -.

Solução

uma.

Primeiro, esboce a região e o sólido da revolução, conforme mostrado.

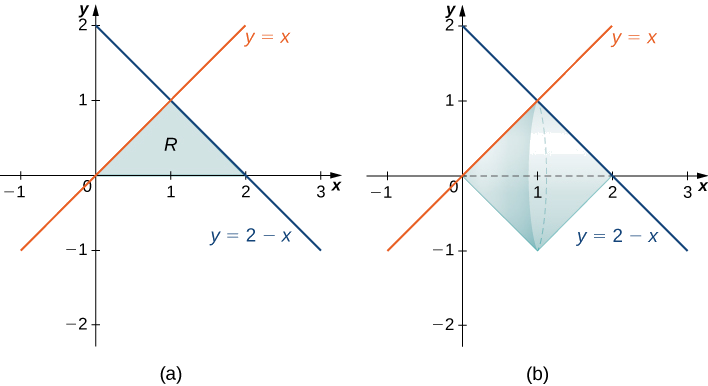
$Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e tem duas linhas y=x e y=2-x desenhadas no primeiro quadrante. As linhas se cruzam em (1,1) e formam um triângulo acima do eixo x. A região que é o triângulo está sombreada. O segundo gráfico é rotulado como “b” e tem os mesmos gráficos de “a”. A região triangular sombreada em “a” foi girada em torno do eixo x para formar um sólido no segundo gráfico.$
Figura$\PageIndex{11}$: (a) A região$R$ delimitada por duas linhas e$x$ pelo eixo. (b) O sólido da revolução gerado pela rotação em$R$ torno do$x$ eixo.

Olhando para a região, se quisermos nos integrar em relação a ela$x$, teríamos que dividir a integral em duas partes, porque temos funções diferentes limitando a região por$[0,1]$$[1,2]$ e. Nesse caso, usando o método de disco, teríamos

\[V=\int ^1_0 π\,x^2\,dx+\int ^2_1 π(2−x)^2\,dx. \nonumber \]

Se usássemos o método shell em vez disso, usaríamos funções de y para representar as curvas, produzindo

\[V=\int ^1_0 2π\,y[(2−y)−y] \,dy=\int ^1_0 2π\,y[2−2y]\,dy. \nonumber \]

Nenhuma dessas integrais é particularmente onerosa, mas como o método shell requer apenas uma integral e o integrando requer menos simplificação, provavelmente devemos usar o método shell nesse caso.

b.

Primeiro, esboce a região e o sólido da revolução, conforme mostrado.

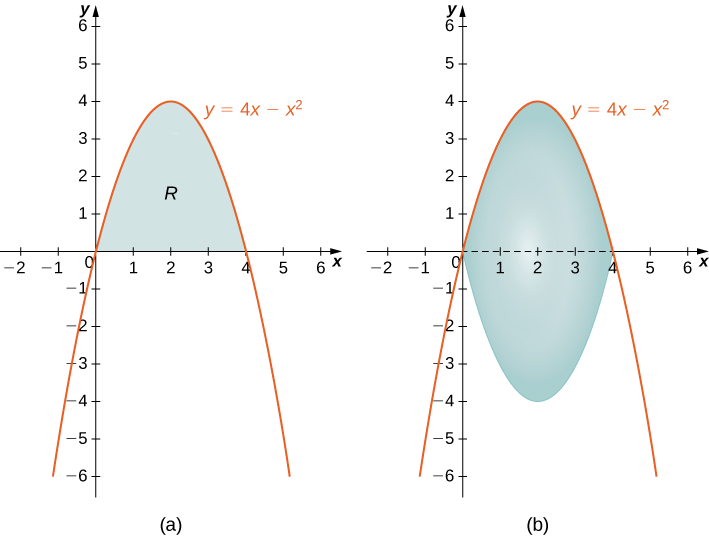
$Essa figura tem dois gráficos. O primeiro gráfico é rotulado como “a” e é a curva y=4x-x^2. É uma parábola invertida que cruza o eixo x na origem e em x=4. A região acima do eixo x e abaixo da curva é sombreada e rotulada como “R”. O segundo gráfico chamado “b” é o mesmo de “a”. Neste gráfico, a região sombreada “R” foi girada em torno do eixo x para formar um sólido.$
Figura$\PageIndex{12}$: (a) A região$R$ entre a curva e o$x$ eixo. (b) O sólido da revolução gerado pela rotação em$R$ torno do$x$ eixo.

Olhando para a região, seria problemático definir um retângulo horizontal; a região é delimitada à esquerda e à direita pela mesma função. Portanto, podemos descartar o método das conchas. O sólido não tem cavidade no meio, então podemos usar o método dos discos. Então

\[V=\int ^4_0π\left(4x−x^2\right)^2\,dx \nonumber \]

Exercício$\PageIndex{6}$

Selecione o melhor método para encontrar o volume de um sólido de revolução gerado pela rotação da região dada em torno do$x$ eixo -e configure a integral para encontrar o volume (não avalie a integral): a região delimitada pelos gráficos de$y=2−x^2$$y=x^2$ e.

Dica

Desenhe a região e use$\PageIndex{12}$ a Figura para decidir qual integral é mais fácil de avaliar.

Responda

Use o método das lavadoras;\[V=\int ^1_{−1}π\left[\left(2−x^2\right)^2−\left(x^2\right)^2\right]\,dx \nonumber \]

Conceitos-chave

O método das conchas cilíndricas é outro método para usar uma integral definida para calcular o volume de um sólido de revolução. Às vezes, esse método é preferível ao método de discos ou ao método de lavadoras porque nos integramos em relação à outra variável. Em alguns casos, uma integral é substancialmente mais complicada do que a outra.

A geometria das funções e a dificuldade da integração são os principais fatores para decidir qual método de integração usar.

Equações-chave

Método de conchas cilíndricas

$\displaystyle V=\int ^b_a\left(2π\,x\,f(x)\right)\,dx$

Glossário

método de conchas cilíndricas

um método para calcular o volume de um sólido de revolução dividindo o sólido em conchas cilíndricas aninhadas; esse método é diferente dos métodos de discos ou arruelas, pois nos integramos em relação à variável oposta

Regra: O método das conchas cilíndricas

Exemplo\(\PageIndex{1}\): The Method of Cylindrical Shells I

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): The Method of Cylindrical Shells II

Exercício\(\PageIndex{2}\)

Regra: O método de conchas cilíndricas para sólidos de revolução em torno do\(x\)-axis

Exemplo\(\PageIndex{3}\): The Method of Cylindrical Shells for a Solid Revolved around the \(x\)-axis

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\): A Region of Revolution Revolved around a Line

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\): A Region of Revolution Bounded by the Graphs of Two Functions

Exercício\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\): Selecting the Best Method

Exercício\(\PageIndex{6}\)

Equações-chave