5.2: A integral definida
- Page ID
- 187934
- Indique a definição da integral definida.
- Explique os termos integrando, limites de integração e variável de integração.
- Explique quando uma função é integrável.
- Descreva a relação entre a integral definida e a área líquida.
- Use a geometria e as propriedades de integrais definidas para avaliá-las.
- Calcule o valor médio de uma função.
Na seção anterior, definimos a área sob uma curva em termos das somas de Riemann:
\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
No entanto, essa definição veio com restrições. Precisávamos\(f(x)\) ser contínuos e não negativos. Infelizmente, os problemas do mundo real nem sempre atendem a essas restrições. Nesta seção, veremos como aplicar o conceito da área sob a curva a um conjunto mais amplo de funções por meio do uso da integral definida.
Definição e notação
A integral definida generaliza o conceito da área sob uma curva. Elevamos os requisitos que\(f(x)\) são contínuos e não negativos e definimos a integral definida da seguinte forma.
Se\(f(x)\) for uma função definida em um intervalo,\([a,b],\) a integral definida de\(f\) de\(a\) até\(b\) é dada por
\[∫^b_af(x)\,dx=\lim_{n→∞} \sum_{i=1}^nf(x^∗_i)Δx, \nonumber \]
desde que o limite exista. Se esse limite existir, diz-se que a função\(f(x)\) é integrável ou é uma função integrável.\([a,b]\)
O símbolo integral na definição anterior deve parecer familiar. Vimos uma notação semelhante no capítulo sobre Aplicações de Derivadas, onde usamos o símbolo integral indefinido (sem o\(a\) e\(b\) acima e abaixo) para representar uma antiderivada. Embora a notação para integrais indefinidas possa parecer semelhante à notação de uma integral definida, elas não são as mesmas. Uma integral definida é um número. Uma integral indefinida é uma família de funções. Mais adiante neste capítulo, examinaremos como esses conceitos estão relacionados. No entanto, deve-se sempre prestar muita atenção à notação para que saibamos se estamos trabalhando com uma integral definida ou uma integral indefinida.
A notação integral remonta ao final do século XVII e é uma das contribuições de Gottfried Wilhelm Leibniz, que muitas vezes é considerado o codescobridor do cálculo, junto com Isaac Newton. O símbolo de integração\(∫\) é alongado\(S\), sugerindo sigma ou soma. Em uma integral definida, acima e abaixo do símbolo de soma estão os limites do intervalo,\([a,b].\) Os números\(a\) e\(b\) são\(x\) valores e são chamados de limites de integração; especificamente,\(a\) é o limite inferior e\(b\) é o limite superior. Para esclarecer, estamos usando o limite de palavras de duas maneiras diferentes no contexto da integral definida. Primeiro, falamos sobre o limite de uma soma como\(n→∞.\) Segundo, os limites da região são chamados de limites de integração.
Chamamos\(f(x)\) a função de integrando, e isso\(dx\) indica que\(f(x)\) é uma função em relação a\(x\), chamada de variável de integração. Observe que, como o índice em uma soma, a variável de integração é uma variável fictícia e não tem impacto no cálculo da integral. Poderíamos usar qualquer variável que quiséssemos como variável de integração:
\[∫^b_af(x)\,dx=∫^b_af(t)\,dt=∫^b_af(u)\,du \nonumber \]
Anteriormente, discutimos o fato de que, se\(f(x)\) for contínuo\([a,b],\), o limite\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) existe e é único. Isso leva ao seguinte teorema, que afirmamos sem prova.
Se\(f(x)\) é contínuo ligado\([a,b]\), então\(f\) é integrável em\([a,b].\)
Funções que não são contínuas ainda\([a,b]\) podem ser integráveis, dependendo da natureza das descontinuidades. Por exemplo, funções com um número finito de descontinuidades de salto ou descontinuidades removíveis em um intervalo fechado são integráveis.
Também é importante notar aqui que mantivemos o uso de uma partição regular nas somas de Riemann. Essa restrição não é estritamente necessária. Qualquer partição pode ser usada para formar uma soma de Riemann. No entanto, se uma partição não regular for usada para definir a integral definida, não é suficiente tomar o limite, pois o número de subintervalos chega ao infinito. Em vez disso, devemos considerar o limite, pois a largura do maior subintervalo vai para zero. Isso introduz uma notação um pouco mais complexa em nossos limites e torna os cálculos mais difíceis sem realmente obter muitos insights adicionais, então optamos por partições regulares para as somas de Riemann.
Use a definição da integral definida para avaliar\(\displaystyle ∫^2_0x^2\,dx.\) Use uma aproximação da extremidade direita para gerar a soma de Riemann.
Solução
Primeiro, queremos estabelecer uma quantia de Riemann. Com base nos limites da integração, temos\(a=0\)\(b=2\) e. Para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular de\([0,2].\) Then
\[Δx=\dfrac{b−a}{n}=\dfrac{2}{n}. \nonumber \]
Como estamos usando uma aproximação do ponto final direito para gerar somas de Riemann, para cada uma\(i\), precisamos calcular o valor da função na extremidade direita do intervalo.\([x_{i−1},x_i].\) A extremidade direita do intervalo é\(x_i\), e uma vez que\(P\) é uma partição regular,
\[x_i=x_0+iΔx=0+i\left[\dfrac{2}{n}\right]=\dfrac{2i}{n}.\nonumber \]
Assim, o valor da função na extremidade direita do intervalo é
\[f(x_i)=x^2_i=\left(\dfrac{2i}{n}\right)^2=\dfrac{4i^2}{n^2}.\nonumber \]
Em seguida, a soma de Riemann assume a forma
\[\sum_{i=1}^nf(x_i)Δx=\sum_{i=1}^n\left(\dfrac{4i^2}{n^2}\right)\dfrac{2}{n}=\sum_{i=1}^n\dfrac{8i^2}{n^3}=\dfrac{8}{n^3}\sum_{i=1}^ni^2.\nonumber \]
Usando a fórmula de soma para\(\displaystyle \sum_{i=1}^ni^2\), temos
\[\begin{align*} \sum_{i=1}^nf(x_i)Δx &=\dfrac{8}{n^3}\sum_{i=1}^ni^2 \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{n(n+1)(2n+1)}{6}\right] \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{2n^3+3n^2+n}{6}\right] \\[4pt] &=\dfrac{16n^3+24n^2+n}{6n^3} \\[4pt] &=\dfrac{8}{3}+\dfrac{4}{n}+\dfrac{1}{6n^2}. \end{align*}\]
Agora, para calcular a integral definida, precisamos considerar o limite como\(n→∞\). Nós recebemos
\ [\ begin {align*} ^2_0x^2dx &=\ lim_ {n→∞}\ sum_ {i=1} ^nf (x_i) Δx\\ [4pt]
&=\ lim_ {n→∞}\ left (\ dfrac {8} {3} +\ dfrac {4} {n} +\ dfrac {1} {6n^2}\ direita)\\ [4pt]
&=\ lim_ {n→∞}\ esquerda (\ dfrac {8} {3}\ direita) +\ lim_ {n→∞}\ esquerda (\ dfrac {4} {n}\ direita) +\ lim_ {n→∞}\ esquerda (\ dfrac {1} {6n^2}\ direita)\\ [[4 pt]
&=\ dfrac {8} {3} +0+0=\ dfrac {8} {3}. \ end {align*}\]
Use a definição da integral definida para avaliar\(\displaystyle ∫^3_0(2x−1)\,dx\).
Use uma aproximação do ponto final direito para gerar a soma de Riemann.
- Dica
-
Use a estratégia de resolução do Example\(\PageIndex{1}\).
- Resposta
-
6
Avaliando integrais definidos
Avaliar integrais definidos dessa forma pode ser bastante entediante devido à complexidade dos cálculos. Mais adiante neste capítulo, desenvolvemos técnicas para avaliar integrais definidas sem limitar as somas de Riemann. No entanto, por enquanto, podemos confiar no fato de que integrais definidas representam a área sob a curva e podemos calcular integrais definidas usando fórmulas geométricas para calcular essa área. Fazemos isso para confirmar que integrais definidas, de fato, representam áreas, então podemos discutir o que fazer no caso de uma curva de uma função cair abaixo do\(x\) eixo.
Use a fórmula para a área de um círculo a ser avaliada\(\displaystyle ∫^6_3\sqrt{9−(x−3)^2}\,dx\).
Solução
A função descreve um semicírculo com raio 3. Para encontrar
\[∫^6_3\sqrt{9−(x−3)^2}\,dx \nonumber \]
queremos encontrar a área abaixo da curva ao longo do intervalo\([3,6].\) A fórmula para a área de um círculo é\(A=πr^2\). A área de um semicírculo é apenas metade da área de um círculo, ou\(A=\dfrac{1}{2}πr^2\). A área sombreada na Figura\(\PageIndex{1}\) cobre a metade do semicírculo, ou\(A=\dfrac{1}{4}πr^2\). Assim,
\[∫^6_3\sqrt{9−(x−3)^2}\,dx=\dfrac{1}{4}π(3)^2=\dfrac{9}{4}π≈7.069. \nonumber \]
![Um gráfico de um semicírculo no quadrante um sobre o intervalo [0,6] com o centro em (3,0). A área abaixo da curva ao longo do intervalo [3,6] está sombreada em azul.](https://math.libretexts.org/@api/deki/files/12421/5.2.1.png)
Use a fórmula para a área de um trapézio para avaliar\(\displaystyle ∫^4_2(2x+3)\,dx\).
- Dica
-
Faça um gráfico da função\(f(x)\) e calcule a área sob a função no intervalo\([2,4].\)
- Resposta
-
18 unidades quadradas
Área e a integral definida
Quando definimos a integral definida, levantamos a exigência de não\(f(x)\) ser negativa. Mas como interpretamos “a área abaixo da curva” quando\(f(x)\) é negativa?
Área assinada na rede
Vamos voltar à soma de Riemann. Considere, por exemplo, a função\(f(x)=2−2x^2\) (mostrada na Figura\(\PageIndex{2}\)) no intervalo\([0,2]\). Use\(n=8\) e escolha {\(x^∗_i\)} como o ponto final esquerdo de cada intervalo. Construa um retângulo em cada subintervalo de altura\(f(x^∗_i)\) e largura\(Δx\). Quando\(f(x^∗_i)\) é positivo, o produto\(f(x^∗_i)Δx\) representa a área do retângulo, como antes. Quando\(f(x^∗_i)\) é negativo, no entanto, o produto\(f(x^∗_i)Δx\) representa o negativo da área do retângulo. A soma de Riemann então se torna
\[\sum_{i=1}^8f(x^∗_i)Δx= (\text{Area of rectangles above the }x\text{-axis})−(\text{Area of rectangles below the }x\text{-axis}) \nonumber \]
![Um gráfico de uma parábola de abertura descendente sobre [-1, 2] com vértice em (0,2) e intercepta x em (-1,0) e (1,0). Oito retângulos são desenhados uniformemente sobre [0,2] com alturas determinadas pelo valor da função nas extremidades esquerdas de cada um.](https://math.libretexts.org/@api/deki/files/2586/CNX_Calc_Figure_05_02_003.jpeg)
Tomando o limite\(n→∞,\) à medida que a soma de Riemann se aproxima da área entre a\(x\) curva acima do\(x\) eixo -e o eixo -, menos a área entre a curva abaixo do\(x\) eixo -e o\(x\) eixo -, conforme mostrado na Figura\(\PageIndex{3}\). Em seguida,
\[\int^2_0f(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=A_1−A_2. \nonumber \]
A quantidade\(A_1−A_2\) é chamada de área líquida assinada.
![Um gráfico de uma parábola de abertura descendente sobre [-2, 2] com vértice em (0,2) e intercepta x em (-1,0) e (1,0). A área no quadrante um abaixo da curva é sombreada em azul e rotulada como A1. A área no quadrante quatro acima da curva e à esquerda de x=2 é sombreada em azul e rotulada como A2.](https://math.libretexts.org/@api/deki/files/2587/CNX_Calc_Figure_05_02_002.jpeg)
Observe que a área líquida assinada pode ser positiva, negativa ou zero. Se a área acima do\(x\) eixo -for maior, a área líquida assinada será positiva. Se a área abaixo do\(x\) eixo -for maior, a área líquida assinada será negativa. Se as áreas acima e abaixo do\(x\) eixo -forem iguais, a área líquida assinada será zero.
Encontre a área líquida sinalizada entre a curva da função\(f(x)=2x\) e o\(x\) eixo -ao longo do intervalo\([−3,3].\)
Solução
A função produz uma linha reta que forma dois triângulos: um de\(x=−3\) para\(x=0\) e outro de\(x=0\) para\(x=3\) (Figura\(\PageIndex{4}\)). Usando a fórmula geométrica para a área de um triângulo,\(A=\dfrac{1}{2}bh\), a área do triângulo\(A_1\), acima do eixo, é
\(A_1=\dfrac{1}{2}3(6)=9\),
onde\(3\) está a base e\(2(3)=6\) é a altura. A área do triângulo\(A_2\), abaixo do eixo, é
\(A_2=\dfrac{1}{2}(3)(6)=9,\)
onde\(3\) está a base e\(6\) é a altura. Assim, a área líquida é
\(\displaystyle ∫^3_{−3}2x\,dx=A_1−A_2=9−9=0.\)
![Um gráfico de uma linha crescente sobre [-6, 6] passando pela origem e (-3, -6) e (3,6). A área abaixo da linha no quadrante um acima de [0,3] é sombreada em azul e rotulada como A1, e a área acima da linha no quadrante três acima de [-3,0] é sombreada em azul e rotulada como A2.](https://math.libretexts.org/@api/deki/files/12422/5.2.2.png)
Análise
Se\(A_1\) for a área acima do\(x\) eixo -e\(A_2\) for a área abaixo do\(x\) eixo -, então a área líquida será\(A_1−A_2\). Como as áreas dos dois triângulos são iguais, a área líquida é zero.
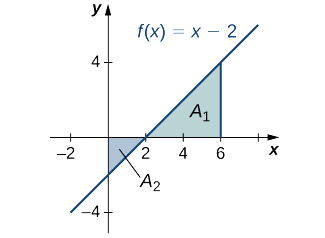
Encontre a área de rede assinada\(f(x)=x−2\) acima do intervalo\([0,6]\), ilustrada na imagem a seguir.
- Dica
-
Use o método de resolução descrito em Exemplo\(\PageIndex{3}\).
- Resposta
-
6
Área total
Uma aplicação da integral definida é encontrar o deslocamento quando é dada uma função de velocidade. Se\(v(t)\) representa a velocidade de um objeto em função do tempo, a área abaixo da curva nos diz a que distância o objeto está de sua posição original. Essa é uma aplicação muito importante da integral definida, e a examinaremos com mais detalhes posteriormente neste capítulo. Por enquanto, vamos dar uma olhada em alguns princípios básicos para ter uma ideia de como isso funciona, estudando velocidades constantes.
Quando a velocidade é constante, a área abaixo da curva é apenas a velocidade vezes o tempo. Essa ideia já é muito familiar. Se um carro se afastar de sua posição inicial em linha reta a uma velocidade de\(70\) mph por\(2\) horas, ele estará a\(140\) quilômetros de distância de sua posição original (Figura\(\PageIndex{5}\)). Usando notação integral, temos
\[∫^2_0 70\,dt=140 \,\text{miles}. \nonumber \]
![Um gráfico no quadrante 1 com o eixo x rotulado como t (horas) e o eixo y rotulado como v (mi/h). A área abaixo da linha v (t) = 75 está sombreada em azul sobre [0,2].](https://math.libretexts.org/@api/deki/files/2590/CNX_Calc_Figure_05_02_015.jpeg)
No contexto do deslocamento, a área líquida sinalizada nos permite levar em consideração a direção. Se um carro viaja direto para o norte a uma velocidade de 60 mph por 2 horas, ele está a 120 milhas ao norte de sua posição inicial. Se o carro então se virar e viajar para o sul a uma velocidade de 40 mph por 3 horas, ele voltará à posição inicial (Figura\(\PageIndex{6}\)). Novamente, usando notação integral, temos
\[\int^2_060\,dt+∫^5_2−40\,dt=120−120=0.\nonumber \]
Nesse caso, o deslocamento é zero.
![Um gráfico nos quadrantes um e quatro com o eixo x rotulado como t (horas) e o eixo y rotulado como v (mi/h). A primeira parte do gráfico é a linha v (t) = 60 sobre [0,2], e a área abaixo da linha no quadrante um está sombreada. A segunda parte do gráfico é a linha v (t) = -40 sobre [2,5], e a área acima da linha no quadrante quatro está sombreada.](https://math.libretexts.org/@api/deki/files/2591/CNX_Calc_Figure_05_02_016.jpeg)
Suponha que queiramos saber até onde o carro viaja em geral, independentemente da direção. Nesse caso, queremos saber a área entre a curva e o\(t\) eixo -, independentemente de essa área estar acima ou abaixo do eixo. Isso é chamado de área total.
Graficamente, é mais fácil pensar em calcular a área total adicionando as áreas acima do eixo e as áreas abaixo do eixo (em vez de subtrair as áreas abaixo do eixo, como fizemos com a área líquida assinada). Para fazer isso matematicamente, usamos a função de valor absoluto. Assim, a distância total percorrida pelo carro é
\[\int^2_0|60|\,dt+∫^5_2|−40|\,dt=∫^2_060\,dt+∫^5_240\,dt=120+120=240.\nonumber \]
Reunindo essas ideias formalmente, declaramos as seguintes definições.
\(f(x)\)Seja uma função integrável definida em um intervalo\([a,b]\). Vamos\(A_1\) representar a área entre\(f(x)\) e o\(x\) eixo -que fica acima do eixo e vamos\(A_2\) representar a área entre\(f(x)\) e o\(x\) eixo -que fica abaixo do eixo. Em seguida, a área líquida assinada entre\(f(x)\) e o\(x\) eixo -é dada por
\[∫^b_af(x)\,dx=A_1−A_2. \nonumber \]
A área total entre\(f(x)\) e o\(x\) eixo -é dada por
\[∫^b_a|f(x)|\,dx=A_1+A_2. \nonumber \]
Encontre a área total entre\(f(x)=x−2\) e o\(x\) eixo -ao longo do intervalo\([0,6].\)
Solução
Calcule o\(x\) -intercept como\((2,0)\) (defina\(y=0,\) solve for\(x\)). Para encontrar a área total, pegue a área abaixo do\(x\) eixo -sobre o subintervalo\([0,2]\) e adicione-a à área acima do\(x\) eixo -no subintervalo\([2,6]\) (Figura\(\PageIndex{7}\)).
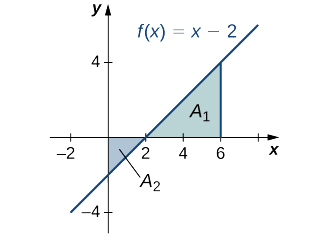
Nós temos
\[∫^6_0|(x−2)|\,dx=A_2+A_1. \nonumber \]
Então, usando a fórmula para a área de um triângulo, obtemos
\[A_2=\dfrac{1}{2}bh=\dfrac{1}{2}⋅2⋅2=2 \nonumber \]
\[A_1=\dfrac{1}{2}bh=\dfrac{1}{2}⋅4⋅4=8. \nonumber \]
A área total, então, é
\[A_1+A_2=8+2=10\,\text{units}^2. \nonumber \]
Encontre a área total entre a função\(f(x)=2x\) e o\(x\) eixo -ao longo do intervalo\([−3,3].\)
- Dica
-
Analise a estratégia de resolução em Example\(\PageIndex{4}\).
- Resposta
-
\(18\,\text{units}^2\)
Propriedades da integral definida
As propriedades das integrais indefinidas também se aplicam às integrais definidas. Integrais definidas também têm propriedades relacionadas aos limites da integração. Essas propriedades, junto com as regras de integração que examinaremos posteriormente neste capítulo, nos ajudam a manipular expressões para avaliar integrais definidas.
1. \[ \begin{equation} ∫^a_af(x)\,dx=0 \end{equation} \nonumber \]
Se os limites de integração forem os mesmos, a integral é apenas uma linha e não contém nenhuma área.
2. \[∫^a_bf(x)\,dx=−∫^b_af(x)\,dx \nonumber \]
Se os limites forem invertidos, coloque um sinal negativo na frente da integral.
3. \[∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx \nonumber \]
A integral de uma soma é a soma das integrais.
4. \[∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx \nonumber \]
A integral de uma diferença é a diferença das integrais.
5. \[∫^b_acf(x)\,dx=c∫^b_af(x)\,dx \nonumber \]
para constante\(c\). A integral do produto de uma constante e de uma função é igual à constante multiplicada pela integral da função.
6. \[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx \nonumber \]
Embora essa fórmula normalmente se aplique quando\(c\) está entre\(a\) e\(b\), a fórmula vale para todos os valores de\(a\)\(b\), e\(c\), desde que\(f(x)\) seja integrável no maior intervalo.
Use as propriedades da integral definida para expressar a integral definida de\(f(x)=−3x^3+2x+2\) sobre o intervalo\([−2,1]\) como a soma de três integrais definidas.
Solução
Usando notação integral, temos Nós\(\displaystyle ∫^1_{−2}(−3x^3+2x+2)\,dx.\) aplicamos as propriedades 3. e 5. para obter
\ [\ begin {align*} ^1_ {−2} (−3x^3+2x+2)\, dx =^1_ {−2} −3x^3\, dx+^1_ {−2} 2x\, dx+^1_ {−2} 2\, dx\\ [4pt]
=−3^1_ {−2} x^3\, dx+2^1_ {−2} x\, dx+^1_ {−2} 2\, dx. \ end {align*}\ nonumber\]
Use as propriedades da integral definida para expressar a integral definida de\(f(x)=6x^3−4x^2+2x−3\) ao longo do intervalo\([1,3]\) como a soma de quatro integrais definidas.
- Dica
-
Use a estratégia de resolução do Example\(\PageIndex{5}\) e as propriedades das integrais definidas.
- Resposta
-
\(\displaystyle 6∫^3_1x^3\,dx−4∫^3_1x^2\,dx+2∫^3_1x\,dx−∫^3_13\,dx \)
Se for sabido disso\(\displaystyle ∫^8_0f(x)\,dx=10\) e\(\displaystyle ∫^5_0f(x)\,dx=5\), encontre o valor de\(\displaystyle ∫^8_5f(x)\,dx\).
Solução
Pela propriedade 6,
\[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx. \nonumber \]
Assim,
\[ \begin{align*} ∫^8_0f(x)\,dx&=∫^5_0f(x)\,dx+∫^8_5f(x)\,dx \\[4pt] 10 &=5+∫^8_5f(x)\,dx \\[4pt] 5 &=∫^8_5f(x)\,dx. \end{align*}\]
Se for sabido que\(\displaystyle ∫^5_1f(x)\,dx=−3\) e\(\displaystyle ∫^5_2f(x)\,dx=4\), encontre o valor de\(\displaystyle ∫^2_1f(x)\,dx.\)
- Dica
-
Use a estratégia de resolução de Example\(\PageIndex{6}\) e a regra sobre propriedades de integrais definidas.
- Resposta
-
\(−7\)
Propriedades de comparação de integrais
Às vezes, uma imagem pode nos dizer mais sobre uma função do que os resultados de cálculos. A comparação de funções por seus gráficos e por suas expressões algébricas geralmente pode fornecer uma nova visão sobre o processo de integração. Intuitivamente, podemos dizer que se uma função\(f(x)\) está acima de outra função\(g(x)\), então a área entre\(f(x)\) e o\(x\) eixo -é maior do que a área entre\(g(x)\) e o\(x\) eixo -. Isso é verdade dependendo do intervalo no qual a comparação é feita. As propriedades das integrais definidas são válidas se\(a<b,\,a=b\), ou\(a>b\). As propriedades a seguir, no entanto, dizem respeito apenas ao caso\(a≤b\) e são usadas quando queremos comparar os tamanhos das integrais.
i. Se for\(f(x)≥0\) para\(a≤x≤b\), então
\[∫^b_af(x)\,dx≥0. \nonumber \]
ii. Se for\(f(x)≥g(x)\) para\(a≤x≤b\), então
\[∫^b_af(x)\,dx≥∫^b_ag(x)\,dx. \nonumber \]
iii. Se\(m\) e\(M\) são constantes tais que\(m≤f(x)≤M\) para\(a≤x≤b\), então
\[m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]
Compare\(f(x)=\sqrt{1+x^2}\) e\(g(x)=\sqrt{1+x}\) ao longo do intervalo\([0,1]\).
Solução
Representar graficamente essas funções é necessário para entender como elas se comparam ao longo do intervalo.\([0,1].\) Inicialmente, quando representadas graficamente em uma calculadora gráfica,\(f(x)\) parece estar acima de\(g(x)\) todos os lugares. No entanto, no intervalo\([0,1]\), os gráficos parecem estar um sobre o outro. Precisamos ampliar para ver isso, no intervalo\([0,1],\,g(x)\) acima\(f(x)\). As duas funções se cruzam em\(x=0\) e\(x=1\) (Figura\(\PageIndex{8}\)).
![Um gráfico da função f (x) = sqrt (1 + x^2) em vermelho e g (x) = sqrt (1 + x) em azul sobre [-2, 3]. A função f (x) aparece acima de g (x), exceto no intervalo [0,1]. Um segundo gráfico ampliado mostra esse intervalo com mais clareza.](https://math.libretexts.org/@api/deki/files/12425/5.2.5.png)
Podemos ver no gráfico que ao longo do intervalo\([0,1],\,g(x)≥f(x)\). Comparando as integrais ao longo do intervalo especificado, também\([0,1],\) vemos isso\(\displaystyle ∫^1_0g(x)\,dx≥∫^1_0f(x)\,dx\) (Figura\(\PageIndex{9}\)). A área fina e sombreada de vermelho mostra quanta diferença existe entre essas duas integrais ao longo do intervalo\([0,1].\)
![Um gráfico mostrando as funções f (x) = sqrt (1 + x^2) e g (x) = sqrt (1 + x) sobre [-3, 3]. A área abaixo de g (x) no quadrante um acima de [0,1] está sombreada. A área abaixo de g (x) e f (x) está incluída nessa área sombreada. O segundo gráfico ampliado mostra com mais clareza que a igualdade entre as funções só se mantém nas extremidades.](https://math.libretexts.org/@api/deki/files/12426/5.2.6.png)
Valor médio de uma função
Muitas vezes precisamos encontrar a média de um conjunto de números, como a nota média do teste. Suponha que você tenha recebido as seguintes notas de teste em sua aula de álgebra: 89, 90, 56, 78, 100 e 69. Sua nota semestral é a média das notas dos testes e você quer saber qual nota esperar. Podemos encontrar a média somando todas as pontuações e dividindo pelo número de pontuações. Nesse caso, há seis resultados de testes. Assim,
\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33. \nonumber \]
Portanto, sua nota média no teste é de aproximadamente 80,33, o que se traduz em B − na maioria das escolas.
Suponha, no entanto, que tenhamos uma função\(v(t)\) que nos dê a velocidade de um objeto a qualquer momento\(t\) e queiramos encontrar a velocidade média do objeto. A função\(v(t)\) assume um número infinito de valores, então não podemos usar o processo que acabamos de descrever. Felizmente, podemos usar uma integral definida para encontrar o valor médio de uma função como essa.
\(f(x)\)Seja contínuo ao longo do intervalo\([a,b]\) e\([a,b]\) seja dividido em n subintervalos de largura\(Δx=(b−a)/n\). Escolha um representante\(x^∗_i\) em cada subintervalo e calcule\(f(x^∗_i)\) para.\(i=1,2,…,n.\) Em outras palavras, considere cada um\(f(x^∗_i)\) como uma amostra da função em cada subintervalo. O valor médio da função pode então ser aproximado como
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}, \nonumber \]
que é basicamente a mesma expressão usada para calcular a média dos valores discretos.
Mas sabemos que\(Δx=\dfrac{b−a}{n},\) sim\(n=\dfrac{b−a}{Δx}\), e temos
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\left(\dfrac{b−a}{Δx}\right)}. \nonumber \]
Seguindo com a álgebra, o numerador é uma soma representada como\(\sum_{i=1}^nf(x∗i),\) e estamos dividindo por uma fração. Para dividir por uma fração, inverta o denominador e multiplique. Assim, um valor aproximado para o valor médio da função é dado por
\[\dfrac{\sum_{i=1}^nf(x^∗_i)}{\left(\dfrac{b−a}{Δx}\right)}=\left(\dfrac{Δx}{b−a}\right)\sum_{i=1}^nf(x^∗_i)=\left(\dfrac{1}{b−a}\right)\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
Esta é uma soma de Riemann. Então, para obter o valor médio exato, pegue o limite que\(n\) vai para o infinito. Assim, o valor médio de uma função é dado por
\[\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx. \nonumber \]
\(f(x)\)Seja contínuo ao longo do intervalo\([a,b]\). Então, o valor médio da função\(f(x)\) (ou\(f_{ave}\)) on\([a,b]\) é dado por
\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)\,dx. \label{averagevalue} \]
Encontre o valor médio de\(f(x)=x+1\) ao longo do intervalo\([0,5].\)
Solução
Primeiro, represente graficamente a função no intervalo indicado, conforme mostrado na Figura\(\PageIndex{10}\).
![Um gráfico no quadrante um mostrando a área sombreada sob a função f (x) = x + 1 sobre [0,5].](https://math.libretexts.org/@api/deki/files/12427/5.2.7.png)
A região é um trapézio deitado de lado, então podemos usar a fórmula da área para um trapézio\(A=\dfrac{1}{2}h(a+b),\) onde\(h\) representa a altura\(a\) e\(b\) representa os dois lados paralelos. Em seguida,
\(\displaystyle ∫^5_0x+1\,dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}\).
Assim, o valor médio da função é
\(\displaystyle \dfrac{1}{5−0}∫^5_0x+1\,dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).
Encontre o valor médio de\(f(x)=6−2x\) ao longo do intervalo\([0,3].\)
- Dica
-
Use a fórmula do valor médio (Equation\ ref {averagevalue}) e use a geometria para avaliar a integral.
- Resposta
-
\(3\)
Conceitos-chave
- A integral definida pode ser usada para calcular a área líquida assinada, que é a área acima do\(x\) eixo -menos a área abaixo do\(x\) eixo -. A área líquida assinada pode ser positiva, negativa ou zero.
- As partes componentes da integral definida são o integrando, a variável de integração e os limites da integração.
- Funções contínuas em um intervalo fechado são integráveis. Funções que não são contínuas ainda podem ser integráveis, dependendo da natureza das descontinuidades.
- As propriedades das integrais definidas podem ser usadas para avaliar integrais.
- A área sob a curva de muitas funções pode ser calculada usando fórmulas geométricas.
- O valor médio de uma função pode ser calculado usando integrais definidas.
Equações-chave
- Integral definido
\(\displaystyle∫^b_af(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\)
- Propriedades da integral definida
\(\displaystyle∫^a_af(x)\,dx=0\)
\(\displaystyle∫^a_bf(x)\,dx=−∫^b_af(x)\,dx\)
\(\displaystyle∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_acf(x)\,dx=c∫^b_af(x)\,dx\), para constante\(c\)
\(\displaystyle∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx\)
Glossário
- valor médio de uma função
- (ou\(f_{ave})\) o valor médio de uma função em um intervalo pode ser encontrado calculando a integral definida da função e dividindo esse valor pelo comprimento do intervalo
- integral definido
- uma operação primária de cálculo; a área entre a curva e o\(x\) eixo -em um determinado intervalo é uma integral definida
- função integrável
- uma função é integrável se o limite que define a integral existir; em outras palavras, se o limite das somas de Riemann\(n\) vai para o infinito existir
- integrando
- a função à direita do símbolo de integração; o integrando inclui a função que está sendo integrada
- limites da integração
- esses valores aparecem perto da parte superior e inferior do sinal integral e definem o intervalo no qual a função deve ser integrada
- área assinada na rede
- a área entre uma função e o\(x\) eixo -de forma que a área abaixo do\(x\) eixo -seja subtraída da área acima do\(x\) eixo -; o resultado é o mesmo que a integral definida da função
- área total
- a área total entre uma função e o\(x\) eixo -é calculada adicionando a área acima do\(x\) eixo -e a área abaixo do\(x\) eixo -; o resultado é o mesmo que a integral definida do valor absoluto da função
- variável de integração
- indica qual variável você está integrando em relação a; se for\(x\), a função no integrando é seguida por\(dx\)


