5.1E: Exercícios para a Seção 5.1

Last updated
Save as PDF

Page ID: 187911

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.) Indique se as somas dadas são iguais ou desiguais.

$\displaystyle \sum_{i=1}^{10}i$e$\displaystyle \sum_{k=1}^{10}k$
$\displaystyle \sum_{i=1}^{10}i$e$\displaystyle \sum_{i=6}^{15}(i−5)$
$\displaystyle \sum_{i=1}^{10}i(i−1)$e$\displaystyle \sum_{j=0}^9(j+1)j$
$\displaystyle \sum_{i=1}^{10}i(i−1)$e$\displaystyle \sum_{k=1}^{10}(k^2−k)$

Responda: a. Eles são iguais; ambos representam a soma dos primeiros 10 números inteiros.
b. Eles são iguais; ambos representam a soma dos primeiros 10 números inteiros.
c. Eles são iguais substituindo$\displaystyle j=i−1.$
d. Eles são iguais; a primeira soma fatora os termos da segunda.

Nos exercícios 2 a 3, use as regras para somas de potências de números inteiros para calcular as somas.

2)$\displaystyle \sum_{i=5}^{10}i$

3)$\displaystyle \sum_{i=5}^{10}i^2$

Responda: $\displaystyle \sum_{i=5}^{10}i^2 = 385−30=355$

Suponha que$\displaystyle \sum_{i=1}^{100}a_i=15$ e$\displaystyle \sum_{i=1}^{100}b_i=−12.$

Nos exercícios 4 a 7, calcule as somas.

4)$\displaystyle \sum_{i=1}^{100}(a_i+b_i)$

5)$\displaystyle \sum_{i=1}^{100}(a_i−b_i)$

Responda: $\displaystyle \sum_{i=1}^{100}(a_i−b_i) = 15−(−12)=27$

6)$\displaystyle \sum_{i=1}^{100}(3a_i−4b_i)$

7)$\displaystyle \sum_{i=1}^{100}(5a_i+4b_i)$

Responda: $\displaystyle \sum_{i=1}^{100}(5a_i+4b_i) = 5(15)+4(−12)=27$

Nos exercícios 8 a 11, use propriedades e fórmulas de soma para reescrever e avaliar as somas.

8)$\displaystyle \sum_{k=1}^{20}100(k^2−5k+1)$

9)$\displaystyle \sum_{j=1}^{50}(j^2−2j)$

Responda: $\displaystyle \sum_{j=1}^{50}j^2−2\sum_{j=1}^{50}j=\frac{(50)(51)(101)}{6}−\frac{2(50)(51)}{2}=40, 375$

10)$\displaystyle \sum_{j=11}^{20}(j^2−10j)$

11)$\displaystyle \sum_{k=1}^{25}[(2k)^2−100k]$

Responda: $\displaystyle 4\sum_{k=1}^{25}k^2−100\sum_{k=1}^{25}k=\frac{4(25)(26)(51)}{9}−50(25)(26)=−10, 400$

Vamos$L_n$ denotar a soma do ponto final esquerdo usando n subintervalos e vamos$R_n$ denotar a soma correspondente do ponto final direito.

Nos exercícios 12 a 19, calcule as somas esquerda e direita indicadas para as funções dadas no intervalo indicado.

12)$L_4$ para$ f(x)=\dfrac{1}{x−1}$ um$ [2,3]$

13)$ R_4$ para$ g(x)=\cos(πx)$ um$ [0,1]$

Resposta: $R_4=0.25$

14)$ L_6$ para$ f(x)=\dfrac{1}{x(x−1)}$ um$ [2,5]$

15)$ R_6$ para$ f(x)=\dfrac{1}{x(x−1)}$ um$ [2,5]$

Resposta: $ R_6=0.372$

16)$ R_4$ para$ \dfrac{1}{x^2+1}$ um$ [−2,2]$

17)$ L_4$ para$ \dfrac{1}{x^2+1}$ um$ [−2,2]$

Resposta: $ L_4=2.20$

18)$ R_4$ para$ x^2−2x+1$ um$ [0,2]$

19)$ L_8$ para$ x^2−2x+1$ um$ [0,2]$

Resposta: $ L_8=0.6875$

20) Calcule as somas de Riemann esquerda e direita -$ L_4$ e$ R_4$, respectivamente - para$ f(x)=(2−|x|)$ em$ [−2,2].$ Calcule seu valor médio e compare-o com a área abaixo do gráfico de$f$.

21) Calcule as somas de Riemann esquerda e direita -$ L_6$ e$ R_6$, respectivamente - para$ f(x)=(3−|3−x|)$ em$ [0,6].$ Calcule seu valor médio e compare-o com a área abaixo do gráfico de$f$.

Resposta: $ L_6=9.000=R_6$. O gráfico de$f$ é um triângulo com área$9\,\text{units}^2$.

22) Calcule as somas de Riemann esquerda$ L_4$ e direita — e$ R_4$, respectivamente — para$ f(x)=\sqrt{4−x^2}$$ [−2,2]$ e compare seus valores.

23) Calcule as somas de Riemann esquerda$ L_6$ e direita — e$ R_6$, respectivamente — para$ f(x)=\sqrt{9−(x−3)^2}$$ [0,6]$ e compare seus valores.

Resposta: $L_6=13.12899=R_6$. Eles são iguais.

Para os exercícios 24 a 27, expresse as seguintes somas finais em notação sigma, mas não as avalie.

24)$ L_{30}$ para$ f(x)=x^2$ um$ [1,2]$

25)$ L_{10}$ para$ f(x)=\sqrt{4−x^2}$ um$ [−2,2]$

Resposta: $\displaystyle L_{10}=\frac{4}{10}\sum_{i=1}^{10}\sqrt{4−(−2+4\frac{(i−1)}{10})}$

26)$ R_{20}$ para$ f(x)=\sin x$ um$ [0,π]$

27)$ R_{100}$ para$\ln x$ um$[1,e]$

Resposta: $\displaystyle R_{100}=\frac{e−1}{100}\sum_{i=1}^{100}ln(1+(e−1)\frac{i}{100})$

Nos exercícios 28 a 33, represente graficamente a função e use uma calculadora ou um programa de computador para avaliar as seguintes somas dos pontos finais esquerdo e direito. A área abaixo da curva entre as extremidades esquerda e direita é somada?

28) [T]$ L_{100}$ e$ R_{100}$ para$ y=x^2−3x+1$ no intervalo$ [−1,1]$

29) [T]$ L_{100}$ e$R_{100}$ para$y=x^2$ no intervalo$[0,1]$

Resposta

$alt$

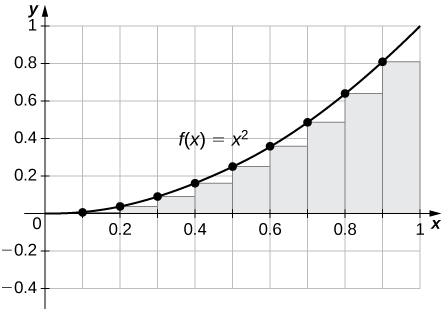
$R_{100}=0.33835,\quad L_{100}=0.32835.$
O gráfico mostra que a soma esquerda de Riemann é subestimada porque a função está aumentando. Da mesma forma, a soma correta de Riemann é uma superestimação. A área fica entre as somas de Riemann à esquerda e à direita. Dez retângulos são mostrados para maior clareza visual. Esse comportamento persiste para mais retângulos.

30) [T]$L_{50}$ e$R_{50}$ para$y=\dfrac{x+1}{x^2−1}$ no intervalo$ [2,4]$

31) [T]$L_{100}$ e$R_{100}$ para$y=x^3$ no intervalo$[−1,1]$

Resposta

$alt$

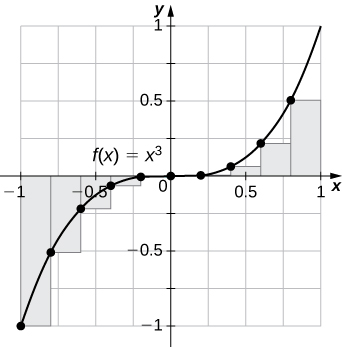
$L_{100}=−0.02,\quad R_{100}=0.02$.
A soma do ponto final esquerdo é subestimada porque a função está aumentando. Da mesma forma, uma aproximação do ponto final à direita é uma superestimação. A área fica entre as estimativas dos pontos finais esquerdo e direito.

32) [T]$L_{50}$ e$R_{50}$ para$y=\tan(x)$ no intervalo$[0,\frac{π}{4}]$

33) [T]$L_{100}$ e$R_{100}$ para$y=e^{2x}$ no intervalo$[−1,1]$

Resposta

$alt$

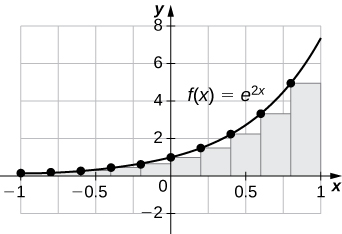
$L_{100}=3.555,\quad R_{100}=3.670$.
O gráfico mostra que a soma esquerda de Riemann é subestimada porque a função está aumentando. Dez retângulos são mostrados para maior clareza visual. Esse comportamento persiste para mais retângulos.

34) Vamos$t_j$ indicar o tempo que Tejay van Garteren levou para subir ao$j^\text{th}$ palco do Tour de France em 2014. Se houvesse um total de 21 estágios, interprete$\displaystyle \sum_{j=1}^{21}t_j$.

35) Vamos$r_j$ indicar a precipitação total em Portland no$j^\text{th}$ dia do ano em 2009. Interpretar$\displaystyle \sum_{j=1}^{31}r_j$.

Resposta: A soma representa a precipitação acumulada em janeiro de 2009.

36) Vamos$d_j$ denotar as horas de luz do dia e$ δ_j$ denotar o aumento das horas de luz do dia$ j−1$ para dia$j$ em Fargo, Dakota do Norte, no$j^\text{th}$ dia do ano. Interpretar$\displaystyle d1+\sum_{j=2}^{365}δ_j.$

37) Para ajudar a entrar em forma, Joe ganha um novo par de tênis de corrida. Se Joe correr 1,6 km por dia na semana 1 e adicionar$\dfrac{1}{10}$ mi à sua rotina diária toda semana, qual é a quilometragem total dos sapatos de Joe após 25 semanas?

Resposta: A quilometragem total é$\displaystyle 7×\sum_{i=1}^{25}(1+\frac{(i−1)}{10})=7×25+\frac{7}{10}×12×25=385$ mi.

38) A tabela a seguir fornece valores aproximados da taxa atmosférica média anual de aumento do dióxido de carbono (CO ₂) a cada década desde 1960, em partes por milhão (ppm). Estime o aumento total do CO ₂ atmosférico entre 1964 e 2013.

Década	ppm/Y
1964-1973	1,07
1976-1983	1,34
1984-1993	1,40
1994-2003	1,87
2004-2013	2,07

Aumento médio anual de CO2 atmosférico, 1964—2013 Fonte: http://www.esrl.noaa.gov/gmd/ccgg/trends/.

39) A tabela a seguir mostra o aumento aproximado do nível do mar em polegadas ao longo de 20 anos a partir de um determinado ano. Estime a mudança líquida no nível médio do mar de 1870 a 2010.

Ano inicial	Mudança de 20 anos
1870	0,3
1890	1,5
1910	0,2
1930	2.8
1950	0.7
1970	1.1
1990	1,5

Aumento aproximado do nível do mar em 20 anos, 1870—1990

Fonte: http://link.springer.com/article/10....712-011-9119-1

Resposta: Adicione os números para obter um aumento líquido de 8,1 polegadas.

40) A tabela a seguir mostra o aumento aproximado em dólares no preço médio de um galão de gás por década desde 1950. Se o preço médio de um galão de gasolina em 2010 foi de $2,60, qual foi o preço médio de um galão de gasolina em 1950?

Ano inicial	Mudança de 10 anos
1950	0,03
1960	0,05
1970	0,86
1980	−0,03
1990	0,29
2000	1,12

Aumentos aproximados do preço do gás em 10 anos, 1950—2000

Fonte: epb.lbl.gov/homepages/Rick_di... 011-trends.pdf.

41) A tabela a seguir mostra o crescimento percentual da população dos EUA a partir de julho do ano indicado. Se a população dos EUA era de 281.421.906 em julho de 2000, estime a população dos EUA em julho de 2010.

Ano	% de variação por ano
2000	1,12
2001	0,99
2002	0,93
2003	0,86
2004	0,93
2005	0,93
2006	0,97
2007	0,96
2008	0,95
2009	0,88

Crescimento percentual anual da população dos EUA, 2000—2009

Fonte: www.census.gov/popest/data.

(Dica: Para obter a população em julho de 2001, multiplique a população em julho de 2000 por 1,0112 para obter 284.573.831.)

Resposta: 309.389.957

Nos exercícios 42 a 45, estime as áreas sob as curvas calculando as somas de Riemann à esquerda,$L_8.$

(42)

$alt$

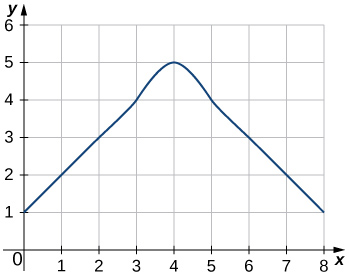
43)

$alt$

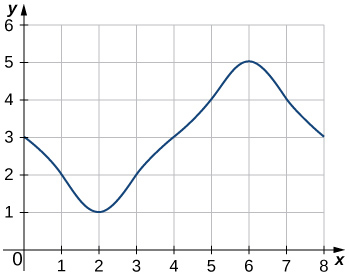
Resposta: $L_8=3+2+1+2+3+4+5+4=24$

44)

$alt$

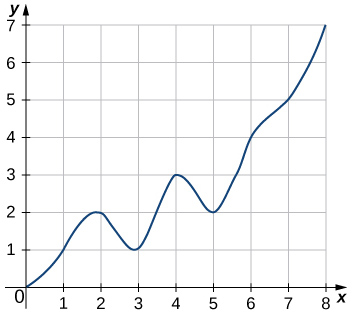
45)

$alt$

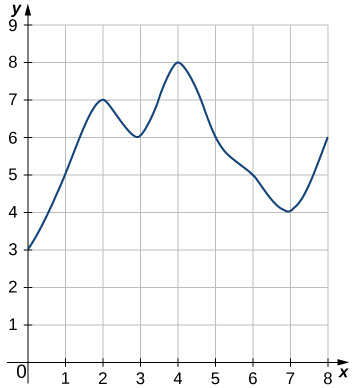
Resposta: $L_8=3+5+7+6+8+6+5+4=44$

46) [T] Use um sistema de álgebra computacional para calcular a soma de Riemann$ L_N$,,$ N=10,30,50$ para$ f(x)=\sqrt{1−x^2}$ em$[−1,1].$

47) [T] Use um sistema de álgebra computacional para calcular a soma de Riemann$L_N$,,$N=10,30,50$ para$f(x)=\dfrac{1}{\sqrt{1+x^2}}$ em$[−1,1].$

Resposta: $L_{10}≈1.7604,\quad L_{30}≈1.7625,\quad L_{50}≈1.76265$

48) [T] Use um sistema de álgebra computacional para calcular a soma de Riemann,$L_N$,$N=10,30,50$ para por$f(x)=\sin^2 x$ diante$ [0,2π]$. Compare essas estimativas com$π$.

Nos exercícios 49-50, use uma calculadora ou um programa de computador para avaliar as somas finais$R_N$ e$L_N$ para$N=1,10,100$. Como essas estimativas se comparam às respostas exatas, que você pode encontrar por meio da geometria?

49) [T]$y=\cos(πx)$ no intervalo$[0,1]$

Resposta: $R_1=−1,\quad L_1=1,$
$R_{10}=−0.1,\quad L_{10}=0.1,$
$L_{100}=0.01,\quad R_{100}=−0.01.$
Pela simetria do gráfico, a área exata é zero.

50) [T]$y=3x+2$ no intervalo$[3,5]$

Nos exercícios 51 a 52, use uma calculadora ou um programa de computador para avaliar as somas dos pontos finais$R_N$ e$L_N$ para$N=1,10,100.$

51) [T]$y=x^4−5x^2+4$ no intervalo$[−2,2]$, que tem uma área exata de$\frac{32}{15}$

Resposta: $R_1=0,\quad L_1=0,$
$R_{10}=2.4499,\quad L_{10}=2.4499,$
$R_{100}=2.1365,\quad L_{100}=2.1365$

52) [T]$y=\ln x$ no intervalo$[1,2]$, que tem uma área exata de$2\ln(2)−1$

53) Explique por que, se$f(a)≥0$ e$f$ estiver aumentando$[a,b]$, que a estimativa do ponto final esquerdo é um limite inferior para a área abaixo do gráfico$f$ de$ [a,b].$

Resposta: Se$[c,d]$ for um subintervalo$ [a,b]$ abaixo de um dos retângulos de soma da extremidade esquerda, a área do retângulo que contribui para a estimativa do ponto final esquerdo é$ f(c)(d−c)$. Mas,$f(c)≤f(x)$ para$c≤x≤d$, então, a área abaixo do gráfico$f$ entre$c$ e$d$ é$f(c)(d−c)$ mais a área abaixo do gráfico,$f$ mas acima do segmento da linha horizontal em altura$f(c)$, o que é positivo. Como isso é verdade para cada intervalo de soma do ponto final esquerdo, segue-se que a soma de Riemann à esquerda é menor ou igual à área abaixo do gráfico$f$ de$[a,b].$

54) Explique por que, se$f(b)≥0$ e f está diminuindo em$ [a,b],$ relação a isso, a estimativa do ponto final esquerdo é um limite superior para a área abaixo do gráfico$f$ de$ [a,b].$

55) Mostre que, em geral,$ R_N−L_N=(b−a)×\dfrac{f(b)−f(a)}{N}.$

Resposta: $\displaystyle L_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i−1}{N})=\frac{b−a}{N}\sum_{i=0}^{N−1}f(a+(b−a)\frac{i}{N})$$\displaystyle R_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i}{N})$e. A soma esquerda tem um termo correspondente a$i=0$ e a soma direita tem um termo correspondente$i=N$ a. No$R_N−L_N$, qualquer termo correspondente a$i=1,2,…,N−1$ ocorre uma vez com um sinal de mais e uma vez com um sinal de menos, então cada um desses termos é cancelado e um fica com$R_N−L_N=\dfrac{b−a}{N}(f(a+(b−a))\dfrac{N}{N})−(f(a)+(b−a)\dfrac{0}{N})=\dfrac{b−a}{N}(f(b)−f(a)).$

56) Explique por que, se$f$ estiver aumentando$[a,b]$, o erro entre$L_N$ ou$R_N$ e a área$A$ abaixo do gráfico de$f$ é no máximo$(b−a)\dfrac{f(b)−f(a)}{N}$.

57) Para cada um dos três gráficos:

a. Obtenha um limite inferior$L(A)$ para a área delimitada pela curva adicionando as áreas dos quadrados completamente delimitadas pela curva.

b. Obtenha um limite superior$U(A)$ para a área adicionando às áreas$L(A)$$B(A)$ dos quadrados parcialmente delimitadas pela curva.

$alt$

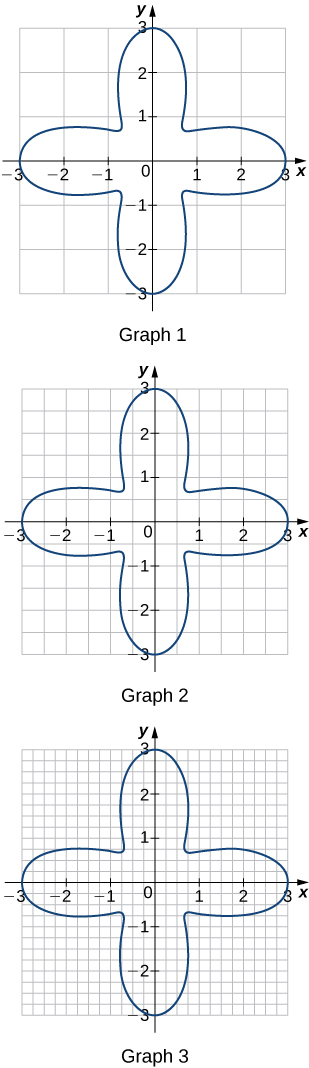
Resposta: Gráfico 1: a.$L(A)=0,\quad B(A)=20; \quad b. U(A)=20.$
Gráfico 2:$a. L(A)=9; \quad b. B(A)=11,\quad U(A)=20.$
Gráfico 3: a.$ L(A)=11.0; \quad b. B(A)=4.5,\quad U(A)=15.5.$

58) No exercício anterior, explique por que não$ L(A)$ fica menor e não$U(A)$ fica maior, pois os quadrados são subdivididos em quatro caixas de igual área.

59) Um círculo unitário é composto por n cunhas equivalentes à cunha interna da figura. A base do triângulo interno é de 1 unidade e sua altura é$\sin(\frac{π}{n}).$ A base do triângulo externo é$B=\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})$ e a altura é$H=B\sin(\frac{2π}{n})$. Use essas informações para argumentar que a área de um círculo unitário é igual a$π.$

$alt$

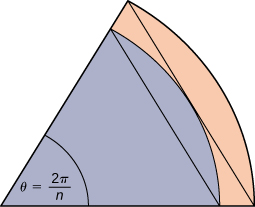
Resposta: $A$Seja a área do círculo unitário. O círculo envolve triângulos$n$ congruentes de cada área$\dfrac{\sin(\dfrac{2π}{n})}{2}$, então,$\frac{n}{2}\sin(\frac{2π}{n})≤A.$ similarmente, o círculo está contido dentro de triângulos$n$ congruentes de cada área$\dfrac{BH}{2}=\frac{1}{2}(\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n}))\sin(\frac{2π}{n})$, então$ A≤\frac{n}{2}\sin(\frac{2π}{n})(\cos(\frac{π}{n}))+\sin(\frac{π}{n})\tan(\frac{π}{n})$. Como$n→∞,\quad \frac{n}{2}\sin(\frac{2π}{n})=\frac{π\sin(\frac{2π}{n})}{(\frac{2π}{n})}→π$, então concluímos$π≤A$. Além disso$ n→∞,\quad \cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})→1$, assim como, também temos$A≤π$. Pelo teorema de compressão para limites, concluímos que$A=π.$