5.1: Aproximando áreas
- Page ID
- 187907
- Use a notação sigma (soma) para calcular somas e potências de números inteiros.
- Use a soma das áreas retangulares para aproximar a área sob uma curva.
- Use somas de Riemann para aproximar a área.
Arquimedes ficou fascinado em calcular as áreas de várias formas — em outras palavras, a quantidade de espaço envolvida pela forma. Ele usou um processo que ficou conhecido como método de exaustão, que usava formas cada vez menores, cujas áreas podiam ser calculadas com exatidão, para preencher uma região irregular e, assim, obter aproximações cada vez mais próximas da área total. Nesse processo, uma área delimitada por curvas é preenchida com retângulos, triângulos e formas com fórmulas de área exata. Essas áreas são então somadas para aproximar a área da região curva.
Nesta seção, desenvolvemos técnicas para aproximar a área entre uma curva, definida por uma função\(f(x),\) e o eixo x em um intervalo fechado.\([a,b].\) Como Arquimedes, primeiro aproximamos a área sob a curva usando formas de área conhecida (ou seja, retângulos). Usando retângulos cada vez menores, aproximamos cada vez mais a área. Tomar um limite nos permite calcular a área exata abaixo da curva.
Vamos começar introduzindo algumas notações para facilitar os cálculos. Em seguida, consideramos o caso quando\(f(x)\) é contínuo e não negativo. Mais adiante neste capítulo, relaxaremos algumas dessas restrições e desenvolveremos técnicas que se aplicam em casos mais gerais.
Notação Sigma (Soma)
Conforme mencionado, usaremos formas de área conhecida para aproximar a área de uma região irregular delimitada por curvas. Esse processo geralmente requer a adição de longas sequências de números. Para facilitar a anotação dessas somas longas, examinamos uma nova notação aqui, chamada notação sigma (também conhecida como notação de soma). A letra maiúscula grega\(Σ\), sigma, é usada para expressar somas longas de valores em uma forma compacta. Por exemplo, se quisermos adicionar todos os números inteiros de 1 a 20 sem notação sigma, temos que escrever
\[1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20. \nonumber \]
Provavelmente poderíamos deixar de escrever alguns termos e escrever
\[1+2+3+4+⋯+19+20, \nonumber \]
o que é melhor, mas ainda assim complicado. Com a notação sigma, escrevemos essa soma como
\[\sum_{i=1}^{20}i \nonumber \]
que é muito mais compacto. Normalmente, a notação sigma é apresentada na forma
\[\sum_{i=1}^{n}a_i \nonumber \]
onde\(a_i\) descreve os termos a serem adicionados e o\(i\) é chamado de\(index\). Cada termo é avaliado e, em seguida, somamos todos os valores, começando com o valor quando\(i=1\) e terminando com o valor quando.\(i=n.\) Por exemplo, uma expressão como\(\displaystyle \sum_{i=2}^{7}s_i\) é interpretada como\(s_2+s_3+s_4+s_5+s_6+s_7\). Observe que o índice é usado apenas para acompanhar os termos a serem adicionados; ele não leva em consideração o cálculo da soma em si. Portanto, o índice é chamado de variável fictícia. Podemos usar qualquer letra que quisermos para o índice. Normalmente, os\(i, \,j, \,k, \,m\) matemáticos usam e\(n\) para índices.
Vamos tentar alguns exemplos de uso da notação sigma.
- Escreva em notação sigma e avalie a soma dos termos\(3^i\) para\(i=1,2,3,4,5.\)
- Escreva a soma em notação sigma:
\[1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}. \nonumber \]
Solução
- Escreva\[\sum_{i=1}^{5}3^i=3+3^2+3^3+3^4+3^5=363. \nonumber \]
- O denominador de cada termo é um quadrado perfeito. Usando a notação sigma, essa soma pode ser escrita como\(\displaystyle \sum_{i=1}^5\dfrac{1}{i^2}\).
Escreva em notação sigma e avalie a soma dos termos\(2^i\) para\(i=3,4,5,6.\)
- Dica
-
Use as etapas de resolução no Exemplo\(\PageIndex{1}\) como guia.
- Resposta
-
\(\displaystyle \sum_{i=3}^{6}2^i=2^3+2^4+2^5+2^6=120\)
As propriedades associadas ao processo de soma são fornecidas na regra a seguir.
Seja\(a_1,a_2,…,a_n\) e\(b_1,b_2,…,b_n\) represente duas sequências de termos e\(c\) seja uma constante. As propriedades a seguir são válidas para todos os números inteiros positivos\(n\) e para números inteiros\(m\), com\(1≤m≤n.\)
- \(\displaystyle \sum_{i=1}^n c=nc\)
- \(\displaystyle \sum_{i=1}^n ca_i=c\sum_{i=1}^na_i\)
- \(\displaystyle \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i\)
- \(\displaystyle \sum_{i=1}^n(a_i−b_i)=\sum_{i=1}^na_i−\sum_{i=1}^nb_i\)
- \(\displaystyle \sum_{i=1}^na_i=\sum_{i=1}^ma_i+\sum_{i=m+1}^na_i\)
Provamos as propriedades (ii.) e (iii.) aqui e deixamos a prova das outras propriedades para os Exercícios.
(ii.) Nós temos
\[\sum_{i=1}^nca_i=ca_1+ca_2+ca_3+⋯+ca_n=c(a_1+a_2+a_3+⋯+a_n)=c\sum_{i=1}^na_i. \nonumber \]
(iii.) Nós temos
\[ \begin{align} \sum_{i=1}^{n}(a_i+b_i) &=(a_1+b_1)+(a_2+b_2)+(a_3+b_3)+⋯+(a_n+b_n) \\[4pt] &=(a_1+a_2+a_3+⋯+a_n)+(b_1+b_2+b_3+⋯+b_n) \\[4pt] &=\sum_{i=1}^na_i+\sum_{i=1}^nb_i. \end {align} \nonumber \]
□
Mais algumas fórmulas para funções encontradas com frequência simplificam ainda mais o processo de soma. Eles são mostrados na próxima regra, para somas e potências de números inteiros, e nós os usamos no próximo conjunto de exemplos.
1. A soma dos\(n\) números inteiros é dada por
\[\sum_{i=1}^n i=1+2+⋯+n=\dfrac{n(n+1)}{2}. \label{sum1} \]
2. A soma dos números inteiros consecutivos ao quadrado é dada por
\[\sum_{i=1}^n i^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6}. \label{sum2} \]
3. A soma dos números inteiros consecutivos ao cubo é dada por
\[\sum_{i=1}^n i^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4}. \label{sum3} \]
Escreva usando a notação sigma e avalie:
- A soma dos termos\((i−3)^2\) para\(i=1,2,…,200.\)
- A soma dos termos\((i^3−i^2)\) para\(i=1,2,3,4,5,6\)
Solução
a. Multiplicando\((i−3)^2\), podemos dividir a expressão em três termos.
\ [\ begin {align*}\ sum_ {i=1} ^ {200} (i−3) ^2 &=\ sum_ {i=1} ^ {200} (i^2−6i+9)\ [4pt]
&=\ sum_ {i=1} ^ {200} i^2−\ sum_ {i=1} ^ {200} 6i+\ sum_ {i=1} ^ {200} 6i+\ sum_ {i=1} =1} ^ {200} 9\\ [4pt]
&=\ sum_ {i=1} ^ {200} i^2−6\ sum_ {i=1} ^ {200} i+\ sum_ {i=1} ^ {200} 9\\ [4pt]
&=\ dfrac {200 (200+1) (400+1)} {6} −6\ esquerda [\ dfrac {200 (200+1)} {2}\ right] +9 (200)\\ [4pt]
&=2.686.700−120.600+1800\\ [4pt]
&=2.567.900\ end {align*}\]
b. Use a propriedade de notação sigma iv. e as regras para a soma dos termos quadrados e a soma dos termos ao cubo.
\ [\ begin {align*}\ sum_ {i=1} ^ {6} (i^3−i^2) &=\ sum_ {i=1} ^6 i^3−\ sum_ {i=1} ^6 i^2\\ [4pt]
&=\ dfrac {6^2 (6+1) ^2} {4} −\ dfrac {6 (6+1) (2 (6) +1)} {6}\\ [4pt]
&=\ dfrac {1764} {4} −\ dfrac {546} {6}\\ [4pt]
&=350\ end {align*}\ nonumber\]
Encontre a soma dos valores de\(4+3i\) for\(i=1,2,…,100.\)
- Dica
-
Use as propriedades da notação sigma para resolver o problema.
- Resposta
-
\(15,550\)
Encontre a soma dos valores de\(f(x)=x^3\) mais de números inteiros\(1,2,3,…,10.\)
Solução
Usando a Equação\ ref {sum3}, temos
\[\sum_{i=0}^{10}i^3=\dfrac{(10)^2(10+1)^2}{4}=\dfrac{100(121)}{4}=3025 \nonumber \]
Avalie a soma indicada pela notação\(\displaystyle \sum_{k=1}^{20}(2k+1)\).
- Dica
-
Use a regra sobre soma e potências de números inteiros (Equações\ ref {sum1} -\ ref {sum3}).
- Resposta
-
\(440\)
Área aproximada
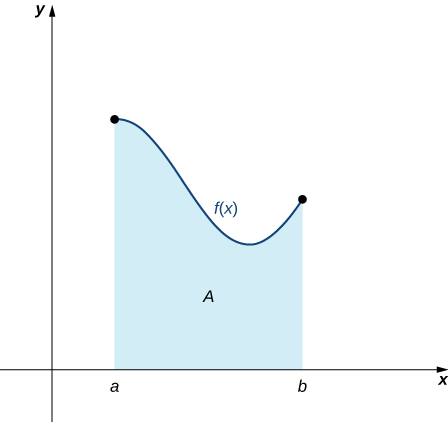
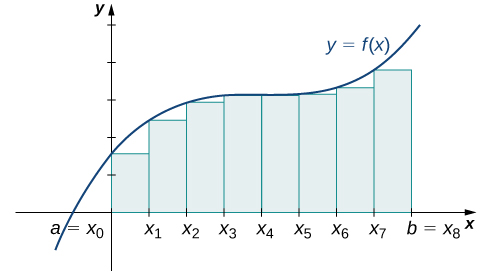
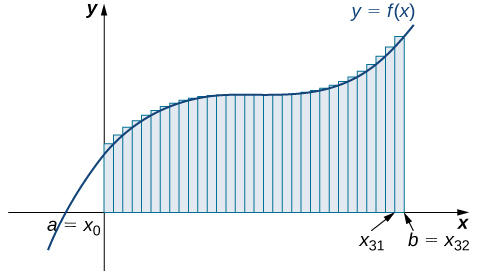
Agora que temos a notação necessária, retornamos ao problema em questão: aproximar a área sob uma curva. \(f(x)\)Seja uma função contínua, não negativa, definida no intervalo fechado\([a,b]\). Queremos aproximar a área\(A\) delimitada por\(f(x)\) cima, o\(x\) eixo -abaixo, a linha\(x=a\) à esquerda e a linha à\(x=b\) direita (Figura\(\PageIndex{1}\)).
Como aproximamos a área sob essa curva? A abordagem é geométrica. Ao dividir uma região em muitas formas pequenas que têm fórmulas de área conhecidas, podemos somar essas áreas e obter uma estimativa razoável da área real. Começamos dividindo o intervalo\([a,b]\) em\(n\) subintervalos de igual largura,\(\dfrac{b−a}{n}\). Fazemos isso selecionando pontos igualmente espaçados\(x_0,x_1,x_2,…,x_n\) com\(x_0=a,x_n=b,\) e
\[x_i−x_{i−1}=\dfrac{b−a}{n} \nonumber \]
para\(i=1,2,3,…,n.\)
Denotamos a largura de cada subintervalo com a notação\(Δx,\) so\(Δx=\frac{b−a}{n}\) e
\[x_i=x_0+iΔx \nonumber \]
for\(i=1,2,3,…,n.\) Essa noção de dividir um intervalo\([a,b]\) em subintervalos selecionando pontos de dentro do intervalo é usada com bastante frequência para aproximar a área sob uma curva, então vamos definir alguma terminologia relevante.
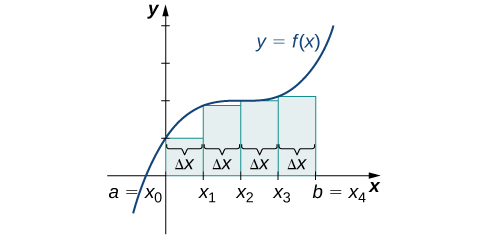
Um conjunto de pontos\(P={x_i}\) para\(i=0,1,2,…,n\) com\(a=x_0 < x_1 < x_2 < ... < x_n = b\), que divide o intervalo\([a, b]\) em subintervalos do formulário,\([x_0, x_1], [x_1, x_2], ..., [x_{n-1}, x_n]\) é chamado de
Podemos usar essa partição regular como base de um método para estimar a área sob a curva. Em seguida, examinamos dois métodos: a aproximação do ponto final esquerdo e a aproximação do ponto final direito.
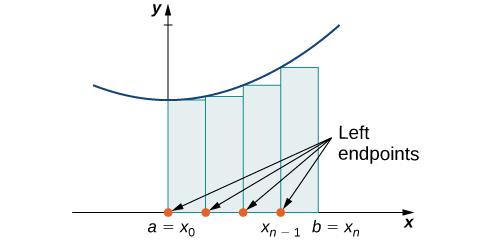
Em cada subintervalo\([x_{i−1},x_i]\) (for\(i=1,2,3,…,n\)), construa um retângulo com largura\(Δx\) e altura iguais a\(f(x_{i−1})\), que é o valor da função na extremidade esquerda do subintervalo. Então, a área desse retângulo é\(f(x_{i−1})Δx\). Somando as áreas de todos esses retângulos, obtemos um valor aproximado para\(A\) (Figura\(\PageIndex{2}\)). Usamos a notação\(L_n\) para indicar que essa é uma aproximação do ponto final esquerdo do\(A\) uso de\(n\) subintervalos.
\[A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\sum_{i=1}^nf(x_{i−1})Δx \nonumber \]
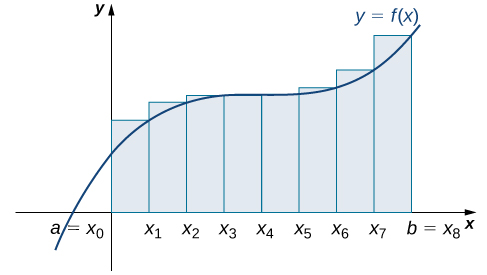
O segundo método para aproximar a área sob uma curva é a aproximação do ponto final direito. É quase o mesmo que a aproximação do ponto final esquerdo, mas agora as alturas dos retângulos são determinadas pelos valores da função à direita de cada subintervalo.
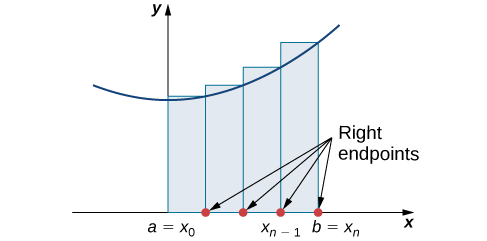
Construa um retângulo em cada subintervalo\([x_{i−1},x_i]\), só que desta vez a altura do retângulo é determinada\(f(x_i)\) pelo valor da função na extremidade direita do subintervalo. Então, a área de cada retângulo é\(f(x_i)\,Δx\) e a aproximação para\(A\) é dada por
\[A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\sum_{i=1}^nf(x_i)Δx. \nonumber \]
A notação\(R_n\) indica que essa é uma aproximação do ponto final direito para\(A\) (Figura\(\PageIndex{3}\)).
Os gráficos na Figura\(\PageIndex{4}\) representam a curva\(f(x)=\dfrac{x^2}{2}\). Na Figura,\(\PageIndex{4b}\) dividimos a região representada pelo intervalo\([0,3]\) em seis subintervalos, cada um com largura\(0.5\). Assim,\(Δx=0.5\). Em seguida, formamos seis retângulos desenhando linhas verticais perpendiculares à\(x_{i−1}\) extremidade esquerda de cada subintervalo. Determinamos a altura de cada retângulo calculando\(f(x_{i−1})\) para\(i=1,2,3,4,5,6.\) Os intervalos são\([0,0.5],[0.5,1],[1,1.5],[1.5,2],[2,2.5],[2.5,3]\). Encontramos a área de cada retângulo multiplicando a altura pela largura. Em seguida, a soma das áreas retangulares se aproxima da área entre\(f(x)\) e o\(x\) eixo. Quando os pontos finais esquerdos são usados para calcular a altura, temos uma aproximação do ponto final esquerdo. Assim,
\ [\ begin {alinhamento*} A≈ L_6 &=\ sum_ {i=1} ^6f (x_ {i−1}) Δx =f (x_0) Δx+f (x_1) ΔX+f (x_2) ΔX+f (x_3) Δx+f (x_4) Δx+f (x_5) Δx\\ [4] pt]
&=f (0) 0,5+f (0,5) 0,5+f (1) 0,5+f (1,5) 0,5+f (2) 0,5+f (2,5) 0,5\\ [4pt]
& =( 0) 0,5+ (0,125) 0,5+ (0,5) 0,5+ (1,125) 0,5+ (2) 0,5+ (3,125) 0,5\\ [4pt]
&=0+0,0625 +0,25+0,5625+1+1,5625\\ [4pt]
&=3,4375\,\ text {unidades} ^2\ end {align*}\ nonumber\]
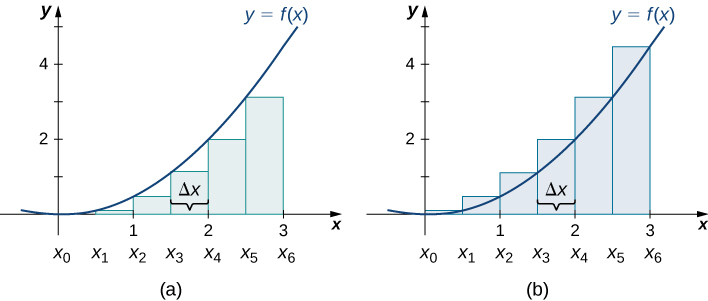
Na Figura\(\PageIndex{4b}\), desenhamos linhas verticais perpendiculares a\(x_i\) tal ponto que\(x_i\) é o ponto final direito de cada subintervalo e calculamos\(f(x_i)\) para\(i=1,2,3,4,5,6\). Multiplicamos cada um\(f(x_i)\) por\(Δx\) para encontrar as áreas retangulares e depois as adicionamos. Esta é uma aproximação do ponto final direito da área abaixo\(f(x)\). Assim,
\ [\ begin {alinhamento*} A≈ R_6 &=\ sum_ {i=1} ^6f (x_i) Δx=F (x_1) Δx+f (x_2) ΔX+f (x_3) Δx+f (x_4) ΔX+f (x_5) ΔX+f (x_6) Δx\\ [4pt]
f (0,5) 0,5+f (1) 0,5+f (1,5) 0,5+f (2) 0,5+f (2,5) 0,5+f (3) 0,5\\ [4pt]
& =( 0,125) 0,5+ (0,5) 0,5+ (1,125) 0,5+ (2) 0,5+ (3,125) 0,5+ (4,5) 0,5\\ [4pt]
&=0,06+ 25+0,25 +0,5625+1+1,5625+2,25\\ [4pt]
&=5,6875\,\ text {unidades} ^2. \ end {align*}\ nonumber\]
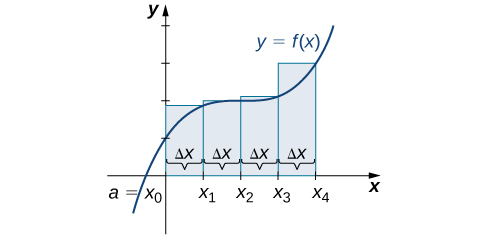
Use as aproximações da extremidade esquerda e da extremidade direita para aproximar a área sob a curva de\(f(x)=x^2\) no intervalo\([0,2]\); use\(n=4\).
Solução
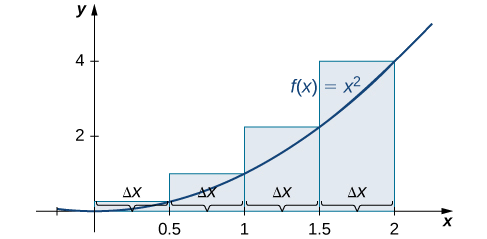
Primeiro, divida o intervalo\([0,2]\) em subintervalos\(n\) iguais. Usando\(n=4,\, Δx=\dfrac{(2−0)}{4}=0.5\). Essa é a largura de cada retângulo. Os intervalos\([0,0.5],[0.5,1],[1,1.5],[1.5,2]\) são mostrados na Figura\(\PageIndex{5}\). Usando uma aproximação do ponto final esquerdo, as alturas são\(f(0)=0,\,f(0.5)=0.25,\,f(1)=1,\) e\(f(1.5)=2.25.\) Então,
\[ \begin{align*} L_4 &=f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+f(x_3)Δx \\[4pt] &=0(0.5)+0.25(0.5)+1(0.5)+2.25(0.5) \\[4pt] &=1.75 \,\text{units}^2 \end{align*} \nonumber \]
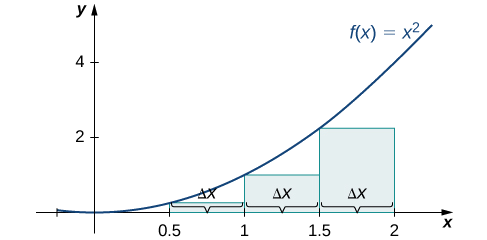
A aproximação do ponto final direito é mostrada na Figura\(\PageIndex{6}\). Os intervalos são os mesmos,\(Δx=0.5,\) mas agora use a extremidade direita para calcular a altura dos retângulos. Nós temos
\[ \begin{align*} R_4 &=f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+f(x_4)Δx \\[4pt] &=0.25(0.5)+1(0.5)+2.25(0.5)+4(0.5) \\[4pt] &=3.75 \,\text{units}^2 \end{align*} \nonumber \]
A aproximação do ponto final esquerdo é\(1.75\,\text{units}^2\); a aproximação do ponto final direito é\(3.75 \,\text{units}^2\).
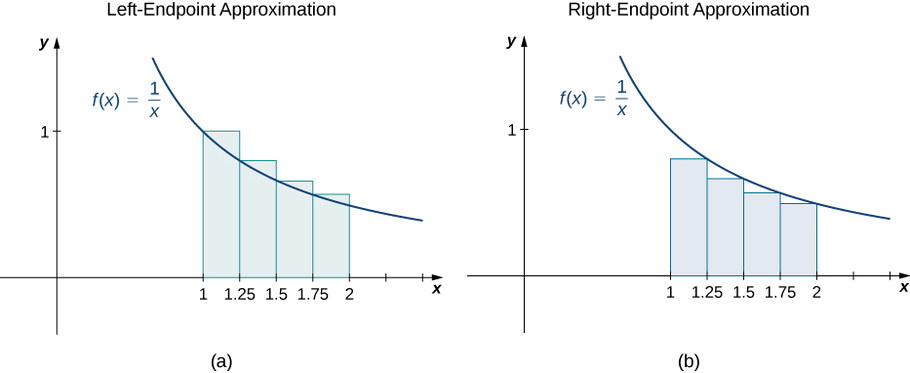
Esboce aproximações do ponto final esquerdo e do ponto final direito para\(f(x)=\dfrac{1}{x}\) usar\(n=4\).\([1,2]\) Aproxime a área usando os dois métodos.
- Dica
-
Siga a estratégia de resolução em Exemplo,\(\PageIndex{4}\) passo a passo.
- Resposta
-
A aproximação do ponto final esquerdo é\(0.7595 \,\text{units}^2\). A aproximação do ponto final direito é\(0.6345 \,\text{units}^2\). Veja a mídia abaixo.
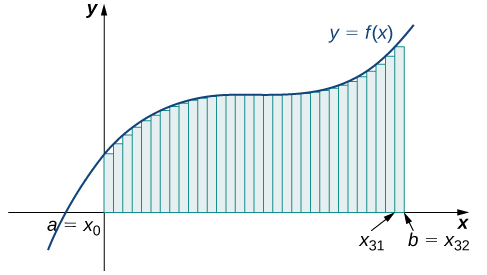
Observando a Figura\(\PageIndex{4}\) e os gráficos em Exemplo\(\PageIndex{4}\), podemos ver que quando usamos um pequeno número de intervalos, nem a aproximação do ponto final esquerdo nem a aproximação do ponto final direito são uma estimativa particularmente precisa da área sob a curva. No entanto, parece lógico que, se aumentarmos o número de pontos em nossa partição, nossa estimativa de\(A\) melhorará. Teremos mais retângulos, mas cada retângulo será mais fino, então poderemos ajustar os retângulos à curva com mais precisão.
Podemos demonstrar a aproximação aprimorada obtida por meio de intervalos menores com um exemplo. Vamos explorar a ideia de aumentar\(n\), primeiro em uma aproximação do ponto final esquerdo com quatro retângulos, depois oito retângulos e, finalmente,\(32\) retângulos. Então, vamos fazer a mesma coisa em uma aproximação da extremidade direita, usando os mesmos conjuntos de intervalos, da mesma região curva. A figura\(\PageIndex{7}\) mostra a área da região abaixo da curva\(f(x)=(x−1)^3+4\) no intervalo\([0,2]\) usando uma aproximação do ponto final esquerdo, onde\(n=4.\) a largura de cada retângulo é
\[Δx=\dfrac{2−0}{4}=\dfrac{1}{2}.\nonumber \]
A área é aproximada pelas áreas somadas dos retângulos, ou
\[L_4=f(0)(0.5)+f(0.5)(0.5)+f(1)(0.5)+f(1.5)0.5=7.5 \,\text{units}^2\nonumber \]
A figura\(\PageIndex{8}\) mostra a mesma curva dividida em oito subintervalos. Comparando o gráfico com quatro retângulos na Figura\(\PageIndex{7}\) com este gráfico com oito retângulos, podemos ver que parece haver menos espaço em branco sob a curva quando\(n=8.\) Esse espaço em branco é uma área abaixo da curva que não podemos incluir usando nossa aproximação. A área dos retângulos é
\[L_8=f(0)(0.25)+f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)=7.75 \,\text{units}^2\nonumber \]
O gráfico na Figura\(\PageIndex{9}\) mostra a mesma função com\(32\) retângulos inscritos sob a curva. Parece haver pouco espaço em branco restante. A área ocupada pelos retângulos é
\[L_{32}=f(0)(0.0625)+f(0.0625)(0.0625)+f(0.125)(0.0625)+⋯+f(1.9375)(0.0625)=7.9375 \,\text{units}^2.\nonumber \]
Podemos realizar um processo semelhante para o método de aproximação do ponto final direito. Uma aproximação do ponto final direito da mesma curva, usando quatro retângulos (Figura\(\PageIndex{10}\)), gera uma área
\[R_4=f(0.5)(0.5)+f(1)(0.5)+f(1.5)(0.5)+f(2)(0.5)=8.5 \,\text{units}^2.\nonumber \]
Dividir a região ao longo do intervalo\([0,2]\) em oito retângulos resulta em\(Δx=\dfrac{2−0}{8}=0.25.\) O gráfico é mostrado na Figura\(\PageIndex{11}\). A área é
\[R_8=f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)+f(2)(0.25)=8.25 \,\text{units}^2\nonumber \]
Por último, a aproximação do ponto final direito com\(n=32\) está próxima da área real (Figura\(\PageIndex{12}\)). A área é de aproximadamente
\[R_{32}=f(0.0625)(0.0625)+f(0.125)(0.0625)+f(0.1875)(0.0625)+⋯+f(2)(0.0625)=8.0625 \,\text{units}^2\nonumber \]
Com base nesses números e cálculos, parece que estamos no caminho certo; os retângulos parecem se aproximar melhor da área abaixo da curva à\(n\) medida que aumentam. Além disso, à medida que\(n\) aumenta, as aproximações da extremidade esquerda e da extremidade direita parecem se aproximar de uma área de unidades\(8\) quadradas. A tabela\(\PageIndex{15}\) mostra uma comparação numérica dos métodos dos pontos extremos esquerdo e direito. A ideia de que as aproximações da área sob a curva ficam\(n\) cada vez melhores à medida que ficam cada vez maiores é muito importante, e agora exploramos essa ideia com mais detalhes.
| Valor de\(n\) | Área aproximada\(L_n\) | Área aproximada\(R_n\) |
|---|---|---|
| \ (n\)” style="alinhamento vertical: médio; ">\(n=4\) | \ (L_n\)” style="alinhamento vertical: médio; ">\(7.5\) | \ (r_n\)” style="alinhamento vertical: médio; ">\(8.5\) |
| \ (n\)” style="alinhamento vertical: médio; ">\(n=8\) | \ (L_n\)” style="alinhamento vertical: médio; ">\(7.75\) | \ (r_n\)” style="alinhamento vertical: médio; ">\(8.25\) |
| \ (n\)” style="alinhamento vertical: médio; ">\(n=32\) | \ (L_n\)” style="alinhamento vertical: médio; ">\(7.94\) | \ (r_n\)” style="alinhamento vertical: médio; ">\(8.06\) |
Formando Riemann Sums
Até agora, usamos retângulos para aproximar a área sob uma curva. As alturas desses retângulos foram determinadas pela avaliação da função nas extremidades direita ou esquerda do subintervalo\([x_{i−1},x_i]\). Na realidade, não há razão para restringir a avaliação da função a apenas um desses dois pontos. Poderíamos avaliar a função em qualquer ponto\(x^∗_i\) do subintervalo\([x_{i−1},x_i]\) e usar\(f(x^∗_i)\) como a altura do nosso retângulo. Isso nos dá uma estimativa da área do formulário
\[A≈\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]
A soma dessa forma é chamada de soma de Riemann, nomeada em homenagem ao matemático do século XIX Bernhard Riemann, que desenvolveu a ideia.
\(f(x)\)Seja definido em um intervalo fechado\([a,b]\) e\(P\) seja qualquer partição de\([a,b]\). \(Δx_i\)Seja a largura de cada subintervalo\([x_{i−1},x_i]\) e, para cada um\(i\),\(x^∗_i\) seja qualquer ponto de entrada\([x_{i−1},\,x_i]\). Uma soma de Riemann é definida\(f(x)\) como
\[\sum_{i=1}^nf(x^∗_i)\,Δx_i. \nonumber \]
Nesse ponto, escolheremos uma partição regular\(P\), como mostramos nos exemplos acima. Isso força tudo\(Δx_i\) a ser igual\(Δx = \dfrac{b-a}{n}\) a qualquer número natural de intervalos\(n\).
Lembre-se de que, com as aproximações dos pontos extremos esquerdo e direito, as estimativas parecem ficar cada vez melhores à medida que\(n\) ficam cada vez maiores. A mesma coisa acontece com as somas de Riemann. As somas de Riemann fornecem melhores aproximações para valores maiores de\(n\). Agora estamos prontos para definir a área sob uma curva em termos de somas de Riemann.
\(f(x)\)Seja uma função contínua e não negativa em um intervalo\([a,b]\) e\(\displaystyle \sum_{i=1}^nf(x^∗_i)\,Δx\) seja uma soma de Riemann para\(f(x)\) com uma partição regular\(P\). Então, a área abaixo da curva\(y=f(x)\) em\([a,b]\) é dada por
\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]
Veja uma demonstração gráfica da construção de uma soma de Riemann.
Algumas sutilezas aqui valem a pena discutir. Primeiro, observe que tomar o limite de uma soma é um pouco diferente de tomar o limite de uma função\(f(x)\) que\(x\) vai para o infinito. Os limites de somas são discutidos em detalhes no capítulo sobre Sequências e Séries; no entanto, por enquanto, podemos supor que as técnicas computacionais que usamos para calcular limites de funções também podem ser usadas para calcular limites de somas.
Em segundo lugar, devemos considerar o que fazer se a expressão convergir para limites diferentes para diferentes escolhas de\({x^∗_i}.\) Felizmente, isso não acontece. Embora a prova esteja além do escopo deste texto, pode-se mostrar que, se\(f(x)\) for contínua no intervalo fechado\([a,b]\),\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) existe e é única (em outras palavras, não depende da escolha de\({x^∗_i}\)).
Analisaremos alguns exemplos em breve. Mas, antes disso, vamos parar um momento e falar sobre algumas opções específicas para\({x^∗_i}\). Embora qualquer opção de nos\({x^∗_i}\) forneça uma estimativa da área abaixo da curva, não sabemos necessariamente se essa estimativa é muito alta (superestimada) ou muito baixa (subestimada). Se for importante saber se nossa estimativa é alta ou baixa, podemos selecionar nosso valor\({x^∗_i}\) para garantir um resultado ou outro.
Se quisermos uma superestimação, por exemplo, podemos escolher\({x^∗_i}\) isso\(i=1,2,3,…,n,\)\(f(x^∗_i)≥f(x)\) para todos\(x∈[x_i−1,x_i]\). Em outras palavras, escolhemos de\({x^∗_i}\) forma que\(i=1,2,3,…,n,\)\(f(x^∗_i)\) for seja o valor máximo da função no intervalo\([x_{i−1},x_i]\). Se selecionarmos dessa\({x^∗_i}\) maneira, a soma de Riemann\(\displaystyle \sum_{i=1}^nf(x^∗_i)Δx\) é chamada de soma superior. Da mesma forma, se quisermos uma subestimativa, podemos escolher\({x∗i}\) que for\(i=1,2,3,…,n,\)\(f(x^∗_i)\) seja o valor mínimo da função no intervalo\([x_{i−1},x_i]\). Nesse caso, a soma de Riemann associada é chamada de soma menor. Observe que, se\(f(x)\) estiver aumentando ou diminuindo ao longo do intervalo\([a,b]\), os valores máximo e mínimo da função ocorrem nos pontos finais dos subintervalos, então as somas superior e inferior são exatamente as mesmas das aproximações dos pontos final esquerdo e direito.
Encontre uma soma menor para\(f(x)=10−x^2\) on\([1,2]\); deixe\(n=4\) subintervalos.
Solução
Com\(n=4\) mais de um intervalo\([1,2], \,Δx=\dfrac{1}{4}\). Podemos listar os intervalos como\([1,1.25],\,[1.25,1.5],\,[1.5,1.75],\)\([1.75,2]\) e. Como a função está diminuindo ao longo do intervalo, a\([1,2],\) Figura mostra que uma soma menor é obtida usando os pontos finais corretos.
![O gráfico de f (x) = 10 − x^2 de 0 a 2. Ele é configurado para uma aproximação à direita da área delimitada pela curva e pelo eixo x em [1, 2], rotulada de a=x0 a x4. Mostra uma soma menor.](https://math.libretexts.org/@api/deki/files/4665/5A.png)
A soma de Riemann é
\ [\ begin {align*}\ sum_ {k=1} ^4 (10−x^2) (0,25) &=0,25 [10− (1,25) ^2+10− (1,5) ^2+10− (1,75) ^2+10− (2) ^2]\\ [4pt]
&=0,25 [8,4375+7,75+6,9375+6]\\ [4pt]
&=7,28\,\ texto {unidades} ^2. \ end {align*}\]
A área de\(7.28\)\(\text{units}^2\) é uma soma menor e uma subestimação.
- Encontre uma soma máxima para\(f(x)=10−x^2\) on\([1,2]\); let\(n=4.\)
- Esboce a aproximação.
- Dica
-
\(f(x)\)está diminuindo\([1,2]\), então os valores máximos da função ocorrem nas extremidades esquerdas dos subintervalos.
- Resposta
-
a. Soma superior=\(8.0313 \,\text{units}^2.\)
b.
![Um gráfico da função f (x) = 10 − x^2 de 0 a 2. É configurado para uma aproximação do ponto final direito sobre a área [1,2], que é rotulada de a=x0 a x4. É uma soma superior.](https://math.libretexts.org/@api/deki/files/4666/15.png)
Encontre uma soma menor para\(f(x)=\sin x\) o intervalo\([a,b]=\left[0,\frac{π}{2} \right]\); deixe\(n=6.\)
Solução
Vamos primeiro examinar o gráfico na Figura\(\PageIndex{14}\) para ter uma ideia melhor da área de interesse.
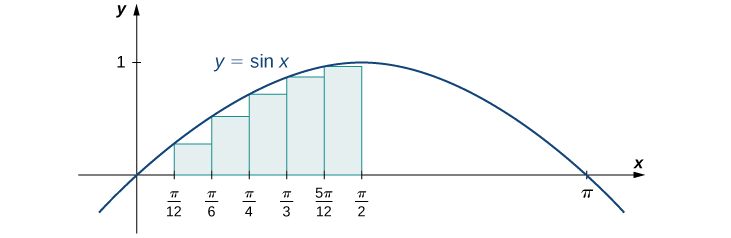
Os intervalos são\(\left[0,\frac{π}{12}\right],\,\left[\frac{π}{12},\frac{π}{6}\right],\,\left[\frac{π}{6},\frac{π}{4}\right],\,\left[\frac{π}{4},\frac{π}{3}\right],\,\left[\frac{π}{3},\frac{5π}{12}\right]\),\(\left[\frac{5π}{12},\frac{π}{2}\right]\) e. Observe que\(f(x)=\sin x\) está aumentando no intervalo\(\left[0,\frac{π}{2}\right]\), então uma aproximação do ponto final esquerdo nos dá a soma mais baixa. Uma aproximação do ponto final esquerdo é a soma de Riemann\(\sum_{i=0}^5\sin x_i\left(\tfrac{π}{12}\right)\). Nós temos
\[A≈\sin(0)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{12}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{6}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{4}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{3}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{5π}{12}\right)\left(\tfrac{π}{12}\right)\approx 0.863 \,\text{units}^2. \nonumber \]
Usando a função\(f(x)=\sin x\) durante o intervalo,\(\left[0,\frac{π}{2}\right],\) encontre uma soma superior; deixe\(n=6.\)
- Dica
-
Siga as etapas do Example\(\PageIndex{6}\).
- Resposta
-
\(A≈1.125 \,\text{units}^2\)
Conceitos-chave
- O uso da notação sigma (soma) do formulário\(\displaystyle \sum_{i=1}^na_i\) é útil para expressar somas longas de valores na forma compacta.
- Para uma função contínua definida em um intervalo,\([a,b],\) o processo de dividir o intervalo em partes\(n\) iguais, estender um retângulo até o gráfico da função, calcular as áreas da série de retângulos e, em seguida, somar as áreas produz uma aproximação da área dessa região.
- Ao usar uma partição normal, a largura de cada retângulo é\(Δx=\dfrac{b−a}{n}\).
- As somas de Riemann são expressões da forma\(\displaystyle \sum_{i=1}^nf(x^∗_i)Δx,\) e podem ser usadas para estimar a área sob a curva. As aproximações dos pontos extremos\(y=f(x).\) esquerdo e direito são tipos especiais de somas de Riemann em que os valores de\({x^∗_i}\) são escolhidos para serem as extremidades esquerda ou direita dos subintervalos, respectivamente.
- As somas de Riemann permitem muita flexibilidade na escolha do conjunto de pontos\({x^∗_i}\) em que a função é avaliada, geralmente com o objetivo de obter uma soma menor ou uma soma superior.
Equações-chave
- Propriedades da notação Sigma
\ [\ begin {align*}\ sum_ {i=1} ^nc&=nc\\ [4pt]
\ sum_ {i=1} ^nca_i &=c\ sum_ {i=1} ^na_i\\ [4pt]
\ sum_ {i=1} ^n (a_i+b_i) &=\ sum_ {i=1} ^na_i+\ sum_ {i=1} ^nb_i\\ [4pt]
\ sum_ {i=1} ^n (a_i−b_i) &=\ sum_ {i=1} ^na_i−\ sum_ {i=1} ^nb_i\\ [4pt]
\ sum_ {i=1} ^na_i&=\ sum_ {i=1} ^ma_i+\ sum_ {i=m+1} ^na_i\ end {align*}\]
- Somas e potências de números inteiros
\[\sum_{i=1}^ni=1+2+⋯+n=\dfrac{n(n+1)}{2} \nonumber \]
\[\sum_{i=1}^ni^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6} \nonumber \]
\[\sum_{i=0}^ni^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4} \nonumber \]
- Aproximação do ponto final esquerdo
\(A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\displaystyle \sum_{i=1}^nf(x_{i−1})Δx\)
- Aproximação do ponto final direito
\(A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\displaystyle \sum_{i=1}^nf(x_i)Δx\)
Glossário
- aproximação do ponto final esquerdo
- uma aproximação da área sob uma curva calculada usando a extremidade esquerda de cada subintervalo para calcular a altura dos lados verticais de cada retângulo
- soma mais baixa
- uma soma obtida usando o valor mínimo de\(f(x)\) em cada subintervalo
- partição
- um conjunto de pontos que divide um intervalo em subintervalos
- partição normal
- uma partição na qual todos os subintervalos têm a mesma largura
- soma de riemann
- uma estimativa da área sob a curva do formulário\(A≈\displaystyle \sum_{i=1}^nf(x^∗_i)Δx\)
- aproximação do ponto final direito
- a aproximação da extremidade direita é uma aproximação da área dos retângulos sob uma curva usando a extremidade direita de cada subintervalo para construir os lados verticais de cada retângulo
- notação sigma
- (também, notação de soma) a letra grega sigma (\(Σ\)) indica a adição dos valores; os valores do índice acima e abaixo do sigma indicam onde começar a soma e onde finalizá-la
- soma superior
- uma soma obtida usando o valor máximo de\(f(x)\) em cada subintervalo


