14.6 : Les dérivées directionnelles et le gradient
- Page ID
- 197326
- Déterminez la dérivée directionnelle dans une direction donnée pour une fonction de deux variables.
- Déterminez le vecteur de gradient d'une fonction à valeur réelle donnée.
- Expliquez l'importance du vecteur de gradient par rapport à la direction du changement le long d'une surface.
- Utilisez le dégradé pour trouver la tangente à une courbe de niveau d'une fonction donnée.
- Calculez des dérivées directionnelles et des gradients en trois dimensions.
Une fonction\(z=f(x,y)\) possède deux dérivées partielles :\(∂z/∂x\) et\(∂z/∂y\). Ces dérivées correspondent à chacune des variables indépendantes et peuvent être interprétées comme des taux de variation instantanés (c'est-à-dire comme des pentes d'une droite tangente). Par exemple,\(∂z/∂x\) représente la pente d'une tangente passant par un point donné de la surface définie\(z=f(x,y),\) en supposant que la tangente est parallèle à l'\(x\)axe. De même,\(∂z/∂y\) représente la pente de la tangente parallèle à l'\(y\)axe. Nous examinons maintenant la possibilité d'une tangente parallèle à aucun des deux axes.
Produits dérivés directionnels
Nous commençons par le graphe d'une surface définie par l'équation\(z=f(x,y)\). Étant donné un point\((a,b)\) dans le domaine de\(f\), nous choisissons la direction à suivre à partir de ce point. Nous mesurons la direction à l'aide d'un angle\(θ\), qui est mesuré dans le sens antihoraire dans le\(xy\) plan, à partir de zéro par rapport à\(x\) l'axe positif (Figure\(\PageIndex{1}\)). La distance que nous parcourons est\(h\) et la direction que nous parcourons sont données par le vecteur unitaire.\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}.\) Par conséquent, la\(z\) coordonnée du deuxième point du graphique est donnée par\(z=f(a+h\cos θ,b+h\sin θ).\)
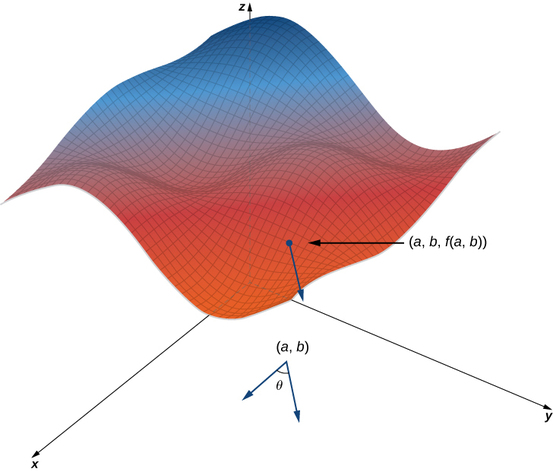
Nous pouvons calculer la pente de la droite sécante en divisant la différence de\(z\) valeurs par la longueur du segment de droite reliant les deux points du domaine. La longueur du segment de ligne est de\(h\). Par conséquent, la pente de la ligne sécante est
\[m_{sec}=\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \]
Pour trouver la pente de la tangente dans la même direction, nous prenons la limite lorsqu'elle\(h\) approche de zéro.
\(z=f(x,y)\)Suppose est une fonction de deux variables avec un domaine de\(D\). Laissez\((a,b)∈D\) et définissez\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Ensuite, la dérivée directionnelle de\(f\) dans la direction de\(\vecs u\) est donnée par
\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h \cos θ,b+h\sin θ)−f(a,b)}{h} \label{DD} \]
à condition que la limite existe.
L'équation \ ref {DD} fournit une définition formelle de la dérivée directionnelle qui peut être utilisée dans de nombreux cas pour calculer une dérivée directionnelle.
Notez que puisque le point\((a, b)\) est choisi aléatoirement dans le domaine\(D\) de la fonction\(f\), nous pouvons utiliser cette définition pour trouver la dérivée directionnelle en fonction de\(x\) et\(y\).
C'est-à-dire,
\[D_{\vecs u}f(x,y)=\lim_{h→0}\dfrac{f(x+h \cos θ,y+h\sin θ)−f(x,y)}{h} \label{DDxy} \]
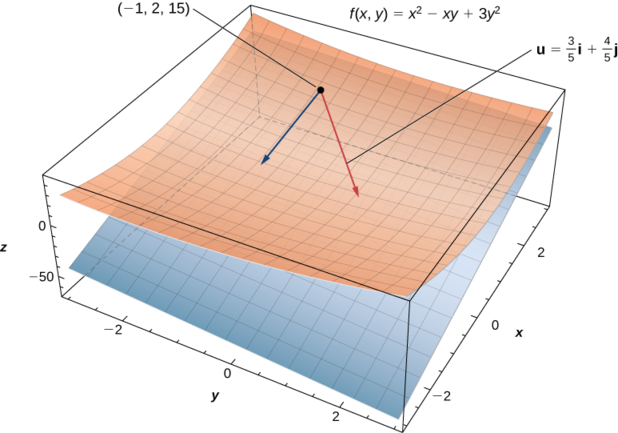
\(θ=\arccos(3/5).\)Détermine la dérivée directionnelle\(D_{\vecs u}f(x,y)\) de\(f(x,y)=x^2−xy+3y^2\) dans la direction de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).
Ensuite, déterminez\(D_{\vecs u}f(−1,2)\).
Solution
Tout d'abord, puisque\(\cos θ=3/5\) et\(θ\) est aigu, cela implique
\[\sin θ=\sqrt{1−\left(\dfrac{3}{5}\right)^2}=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}. \nonumber \]
En utilisant\(f(x,y)=x^2−xy+3y^2,\) nous calculons d'abord\(f(x+h\cos θ,y+h\sin θ)\) :
\ [\ begin {align*} f (x+h \ cos θ, y+h \ sin θ) &= (x+h \ cos θ) ^2− (x+h \ cos θ) (y+h \ sin θ) +3 (y+h \ sin θ) ^2 \ \
&=x^2+2xh \ cos θ+h^2 \ cos^2 θ−xy−xh \ sin θ−yh \ cos θ−h^2 \ sin θ \ cos θ+3y^2+6yh \ sin θ+3h^2 \ sin^2 θ \ \
&=x^2+2xh (\ frac {3} {5}) + \ frac {9h^2} {25} −xy− \ frac {4xh} {5} − \ frac {3yh} {5} − \ frac {12 h ^2} {25} +3y^2+6h (\ frac {4} {5}) +3h^2 (\ frac {16} {25}) \ \
&=x^2−xy+3y^2+ \ frac {2xh} {5} + \ frac {9h^2} {5} + \ frac {21yh} {5}. \ end {align*} \]
Nous substituons cette expression dans l'équation \ ref {DD} par\(a = x\) et\(b = y\) :
\ [\ begin {align*} D_ {\ vecs u} f (x, y) &= \ lim_ {h→0} \ frac {f (x+h \ cos θ, y+h \ sin θ) −f (x, y)} {h} \ \
&= \ lim_ {h→0} \ frac {(x^2−xy+3y^2+ \ frac {2x2→0} h} {5} + \ frac {9h^2} {5} + \ frac {21yh} {5}) − (x^2−xy+3y^2)} {h} \ \
&= \ lim_ {h→0} \ frac {2xh} {5} + \ frac {9h^2} {5} + \ frac {21h} 5}} {h} \ \
et ; = \ lim_ {h→0} \ frac {2x} {5} + \ frac {9h} {5} + \ frac {21 ans} {5} \ \
&= \ frac {2x+21 ans} {5}. \ end {align*} \]
Pour calculer,\(D_{\vecs u}f(−1,2),\) nous\(y=2\) remplaçons\(x=−1\) et dans cette réponse (Figure\(\PageIndex{2}\)) :
\[ D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8. \nonumber \]
Une approche plus simple pour calculer des dérivées directionnelles impliquant des dérivées partielles est décrite dans le théorème suivant.
\(z=f(x,y)\)Soyons une fonction de deux variables\(x\) et\(y\), et supposons que cela\(f_x\)\(f_y\) existe. Ensuite, la dérivée directionnelle de\(f\) dans la direction de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\) est donnée par
\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \label{DD2v} \]
En appliquant la définition d'une dérivée directionnelle énoncée ci-dessus dans l'équation \ ref {DD}, la dérivée directionnelle de\(f\)\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\) dans la direction d'\((x_0, y_0)\)en un point du domaine de\(f\) peut être écrite
\[D_{\vecs u}f((x_0, y_0))=\lim_{t→0}\dfrac{f(x_0+t \cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]
Laissez\(x=x_0+t\cos θ\)\(y=y_0+t\sin θ,\) et définissez\(g(t)=f(x,y)\). Puisque\(f_x\) les\(f_y\) deux existent, nous pouvons utiliser la règle de chaîne pour les fonctions de deux variables afin de calculer\(g′(t)\) :
\[g′(t)=\dfrac{∂f}{∂x}\dfrac{dx}{dt}+\dfrac{∂f}{∂y}\dfrac{dy}{dt}=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]
Si\(t=0,\) alors\(x=x_0\) et\(y=y_0,\) ainsi
\[g′(0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ \nonumber \]
Selon la définition de\(g′(t),\), il est également vrai que
\[g′(0)=\lim_{t→0}\dfrac{g(t)−g(0)}{t}=\lim_{t→0}\dfrac{f(x_0+t\cos θ,y_0+t\sin θ)−f(x_0,y_0)}{t}. \nonumber \]
Par conséquent,\(D_{\vecs u}f(x_0,y_0)=f_x(x_0,y_0)\cos θ+f_y(x_0,y_0)\sin θ\).
Comme le point\( (x_0,y_0) \) est un point arbitraire du domaine de\(f\), ce résultat est valable pour tous les points du domaine\(f\) pour lesquels les partiels\(f_x\) et\(f_y\) existent.
Par conséquent,\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ. \nonumber \]
□
\(θ=\arccos (3/5).\)Détermine la dérivée directionnelle\(D_{\vecs u}f(x,y)\) de\(f(x,y)=x^2−xy+3y^2\) dans la direction de\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\).
Ensuite, déterminez\(D_{\vecs u}f(−1,2)\).
Solution
Il faut d'abord calculer les dérivées partielles de\(f\) :
\[\begin{align*}f_x(x,y) &=2x−y \\ f_y(x,y) &=−x+6y, \end{align*}\]
Ensuite, nous utilisons l'équation \ ref {DD2v} avec\(θ=\arccos (3/5)\) :
\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y) \ cos θ+f_y (x, y) \ sin θ \ \
& =( 2x−y) \ dfrac {3} {5} + (−x+6y) \ dfrac {4} {5} \ \
&= \ dfrac {6x} {5} − \ dfrac {3 ans} {5} − \ dfrac {4} {5} + \ dfrac {24 ans} {5} \ \
&= \ dfrac {2x+21 ans} {5}. \ end {align*} \]
Pour calculer le\(D_{\vecs u}f(−1,2),\) loyer\(x=−1\) et\(y=2\) :
\[D_{\vecs u}f(−1,2)=\dfrac{2(−1)+21(2)}{5}=\dfrac{−2+42}{5}=8.\nonumber \]
Il s'agit de la même réponse obtenue dans l'exemple\(\PageIndex{1}\).
Trouvez la dérivée directionnelle\(D_{\vecs u}f(x,y)\) de\(f(x,y)=3x^2y−4xy^3+3y^2−4x\) dans le sens de\(\vecs u=(\cos \dfrac{π}{3})\,\hat{\mathbf i}+(\sin \dfrac{π}{3})\,\hat{\mathbf j}\) l'utilisation de l'équation \ ref {DD2v}.
Qu'est-ce que\(D_{\vecs u} f(3,4)\) ?
- Allusion
-
Calculez les dérivées partielles et déterminez la valeur de\(θ\).
- Réponse
-
\(D_{\vecs u}f(x,y)=\dfrac{(6xy−4y^3−4)(1)}{2}+\dfrac{(3x^2−12xy^2+6y)\sqrt{3}}{2}\)
\(D_{\vecs u}f(3,4)=\dfrac{72−256−4}{2}+\dfrac{(27−576+24)\sqrt{3}}{2}=−94−\dfrac{525\sqrt{3}}{2}\)
Si le vecteur donné pour la direction de la dérivée n'est pas un vecteur unitaire, il suffit de le diviser par la norme du vecteur. Par exemple, si nous voulions trouver la dérivée directionnelle de la fonction dans Example\(\PageIndex{2}\) dans la direction du vecteur\(⟨−5,12⟩\), nous devons d'abord diviser par sa magnitude pour obtenir\(\vecs u\). Cela nous donne\(\vecs u=⟨−\frac{5}{13},\frac{12}{13}⟩\).
Alors
\ [\ begin {align*} D_ {\ vecs u} f (x, y) &=f_x (x, y) \ cos θ+f_y (x, y) \ sin θ \ \
&=− \ dfrac {5} {13} (2x−y) + \ dfrac {12} {13} (−x+6y) \ \ &=− \ dfrac {12} {13} (−x+6y) \ \
&=− \ dfrac {12} {13} (−x+6y) \ \ &=− \ dfrac {22} {13} x+ \ dfrac {17} {13} y \ end {align*} \]
dégradé
Le côté droit de l'équation \ ref {DD2v} est égal à\(f_x(x,y)\cos θ+f_y(x,y)\sin θ\), qui peut être écrit comme le produit scalaire de deux vecteurs. Définissez le premier vecteur comme\(\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\) et le second vecteur comme\(\vecs u=(\cos θ)\,\hat{\mathbf i}+(\sin θ)\,\hat{\mathbf j}\). Ensuite, le côté droit de l'équation peut être écrit comme le produit scalaire de ces deux vecteurs :
\[D_{\vecs u}f(x,y)=\vecs ∇f(x,y)⋅\vecs u. \label{gradDirDer} \]
Le premier vecteur de l'équation \ ref {GradDirder} porte un nom spécial : le dégradé de la fonction\(f\). Le symbole\(∇\) s'appelle nabla et le vecteur\(\vecs ∇f\) se lit « del »\(f\).
\(z=f(x,y)\)Soyons fonction de\(x\) cela\(f_x\) et\(f_y\) existons.\(y\) Le vecteur\(\vecs ∇f(x,y)\) est appelé gradient de\(f\) et est défini comme
\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}. \label{grad} \]
Le vecteur\(\vecs ∇f(x,y)\) est également écrit « grad »\(f\).
Trouvez le dégradé\(\vecs ∇f(x,y)\) de chacune des fonctions suivantes :
- \(f(x,y)=x^2−xy+3y^2\)
- \(f(x,y)=\sin 3 x \cos 3y\)
Solution
Pour les deux parties a. et b., nous calculons d'abord les dérivées partielles\(f_y\),\(f_x\) puis nous utilisons l'équation \ ref {grad}.
a.\( f_x(x,y)=2x−y\) et\(f_y(x,y)=−x+6y\), donc
\[\begin{align*} \vecs ∇f(x,y) &=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\\ &=(2x−y)\,\hat{\mathbf i}+(−x+6y)\,\hat{\mathbf j}.\end{align*}\]
b.\( f_x(x,y)=3\cos 3x \cos 3y\)\(f_y(x,y)=−3\sin 3x \sin 3y\) et donc
\ [\ begin {align*} \ vecs f (x, y) &=f_x (x, y) \, \ hat {\ mathbf i} +f_y (x, y) \, \ hat {\ mathbf j} \ \
& =( 3 \ cos 3x \ cos 3y) \, \ hat {\ mathbf i} − (3 \ sin 3x \ sin 3y) y) \, \ hat {\ mathbf j}. \ end {align*} \]
Trouvez le dégradé\(\vecs ∇f(x,y)\) de\(f(x,y)=\dfrac{x^2−3y^2}{2x+y}\).
- Allusion
-
Calculez les dérivées partielles, puis utilisez l'équation \ ref {grad}.
- Réponse
-
\(\vecs ∇f(x,y)=\dfrac{2x^2+2xy+6y^2}{(2x+y)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2}{(2x+y)^2}\,\hat{\mathbf j}\)
Le dégradé possède certaines propriétés importantes. Nous avons déjà vu une formule qui utilise le gradient : la formule de la dérivée directionnelle. Rappelons de The Dot Product que si l'angle entre deux vecteurs\(\vecs a\) et\(\vecs b\) est\(φ\),\(\vecs a⋅\vecs b=‖\vecs a‖‖\vecs b‖\cos φ.\) alors, si l'angle entre\(\vecs ∇f(x_0,y_0)\) et\(\vecs u=(cosθ)\,\hat{\mathbf i}+(sinθ)\,\hat{\mathbf j}\) est\(φ\), nous avons
\[D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=\|\vecs ∇f(x_0,y_0)\|‖\vecs u‖\cos φ=\|\vecs ∇f(x_0,y_0)\|\cos φ. \nonumber \]
Le\(‖\vecs u‖\) disparaît car il\(\vecs u\) s'agit d'un vecteur unitaire. Par conséquent, la dérivée directionnelle est égale à l'amplitude du gradient évalué en\((x_0,y_0)\) multipliant par\(\cos φ\). Rappelez-vous que cela\(\cos φ\) va de\(−1\) à\(1\).
Si\(φ=0,\) alors\(\cos φ=1\)\(\vecs ∇f(x_0,y_0)\) et si\(\vecs u\) les deux pointent dans la même direction.
Si\(φ=π\), alors\(\cos φ=−1\)\(\vecs ∇f(x_0,y_0)\) et\(\vecs u\) pointez dans des directions opposées.
Dans le premier cas, la valeur de\(D_{\vecs u}f(x_0,y_0)\) est maximisée ; dans le second cas, la valeur de\(D_{\vecs u}f(x_0,y_0)\) est minimisée.
Nous pouvons également voir que si\(\vecs ∇f(x_0,y_0)=\vecs 0\), alors
\[ D_{\vecs u}f(x_0,y_0)=\vecs ∇f(x_0,y_0)⋅\vecs u=0 \nonumber \]
pour n'importe quel vecteur\(\vecs u\). Ces trois cas sont décrits dans le théorème suivant.
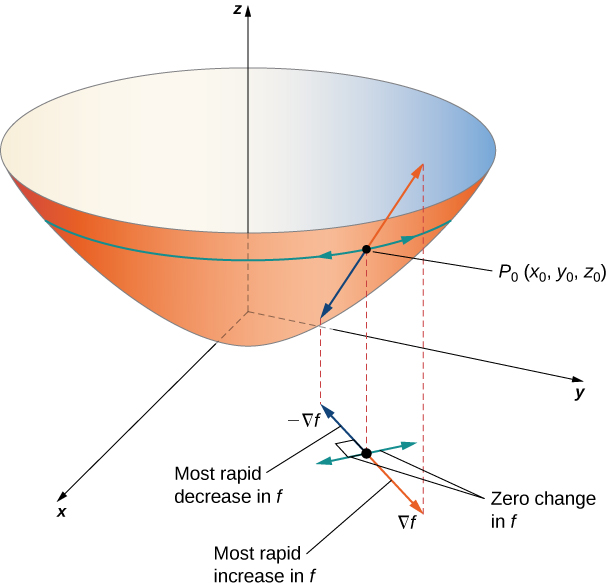
Supposons que la fonction\(z=f(x,y)\) soit dérivable à\((x_0,y_0)\) (Figure\(\PageIndex{3}\)).
- Si\(\vecs ∇f(x_0,y_0)=\vecs 0\), alors\(D_{\vecs u}f(x_0,y_0)=0\) pour n'importe quel vecteur unitaire\(\vecs u\).
- Si\(\vecs ∇f(x_0,y_0)≠ \vecs 0\), alors\(D_{\vecs u}f(x_0,y_0)\) est maximisé lorsque\(\vecs u\) pointe dans la même direction que\(\vecs ∇f(x_0,y_0)\). La valeur maximale de\(D_{\vecs u}f(x_0,y_0)\) est\(\|\vecs ∇f(x_0,y_0)\|\).
- Si\(\vecs ∇f(x_0,y_0)≠\vecs 0\), alors\(D_{\vecs u}f(x_0,y_0)\) est minimisé lorsque\(\vecs u\) pointe dans la direction opposée à\(\vecs ∇f(x_0,y_0)\). La valeur minimale de\(D_{\vecs u}f(x_0,y_0)\) est\(−\|\vecs ∇f(x_0,y_0)\|\).
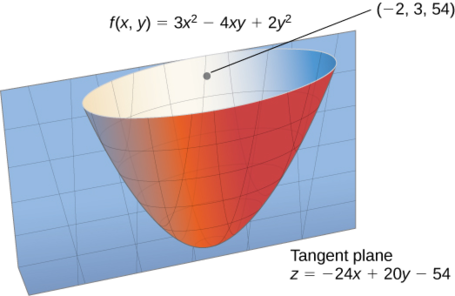
Détermine la direction pour laquelle la dérivée directionnelle de\(f(x,y)=3x^2−4xy+2y^2\) at\((−2,3)\) est maximale. Quelle est la valeur maximale ?
Solution
La valeur maximale de la dérivée directionnelle se produit lorsque\(\vecs ∇f\) et le vecteur unitaire pointe dans la même direction. Par conséquent, nous commençons par calculer\(\vecs ∇f(x,y\)) :
\[f_x(x,y)=6x−4y \; \text{and}\; f_y(x,y)=−4x+4y \nonumber \]
donc
\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}=(6x−4y)\,\hat{\mathbf i}+(−4x+4y)\,\hat{\mathbf j}. \nonumber \]
Ensuite, nous évaluons le gradient à\((−2,3)\) :
\[\vecs ∇f(−2,3)=(6(−2)−4(3))\,\hat{\mathbf i}+(−4(−2)+4(3))\,\hat{\mathbf j}=−24\,\hat{\mathbf i}+20\,\hat{\mathbf j}. \nonumber \]
Nous devons trouver un vecteur unitaire qui pointe dans la même direction. L'étape suivante consiste à diviser\(\vecs ∇f(−2,3)\) par sa magnitude, c'est-à-dire\(\sqrt{(−24)^2+(20)^2}=\sqrt{976}=4\sqrt{61}\).\(\vecs ∇f(−2,3),\) Par conséquent,
\[\dfrac{\vecs ∇f(−2,3)}{\|\vecs ∇f(−2,3)\|}=\dfrac{−24}{4\sqrt{61}}i+\dfrac{20}{4\sqrt{61}}j=−\dfrac{6\sqrt{61}}{61}\,\hat{\mathbf i}+\dfrac{5\sqrt{61}}{61}\,\hat{\mathbf j}. \nonumber \]
Il s'agit du vecteur unitaire qui pointe dans la même direction que\(\vecs ∇f(−2,3).\) Pour trouver l'angle correspondant à ce vecteur unitaire, nous résolvons les équations
\[\cos θ=\dfrac{−6\sqrt{61}}{61}\; \text{and}\; \sin θ=\dfrac{5\sqrt{61}}{61} \nonumber \]
pour\(θ\). Comme le cosinus est négatif et que le sinus est positif, l'angle doit se situer dans le deuxième quadrant. Donc,\(θ=π−\arcsin((5\sqrt{61})/61)≈2.45\) rad.
La valeur maximale de la dérivée directionnelle à\((−2,3)\) est\(\|\vecs ∇f(−2,3)\|=4\sqrt{61}\) (Figure\(\PageIndex{4}\)).
Détermine la direction pour laquelle la dérivée directionnelle de\(g(x,y)=4x−xy+2y^2\) at\((−2,3)\) est maximale. Quelle est la valeur maximale ?
- Allusion
-
Evaluez le gradient\(g\) d'un point\((−2,3)\).
- Réponse
-
Le gradient de\(g\) at\((−2,3)\) est\(\vecs ∇g(−2,3)=\,\hat{\mathbf i}+14\,\hat{\mathbf j}\). Le vecteur unitaire qui pointe dans la même direction\(\vecs ∇g(−2,3)\) que
\[\dfrac{\vecs ∇g(−2,3)}{\|\vecs ∇g(−2,3)\|}=\dfrac{1}{\sqrt{197}}\,\hat{\mathbf i}+\dfrac{14}{\sqrt{197}}\,\hat{\mathbf j}=\dfrac{\sqrt{197}}{197}\,\hat{\mathbf i}+\dfrac{14\sqrt{197}}{197}\,\hat{\mathbf j},\nonumber \]
ce qui donne un angle de\(θ=\arcsin ((14\sqrt{197})/197)≈1.499\) vue.
La valeur maximale de la dérivée directionnelle est\(\|\vecs ∇g(−2,3)\|=\sqrt{197}\).
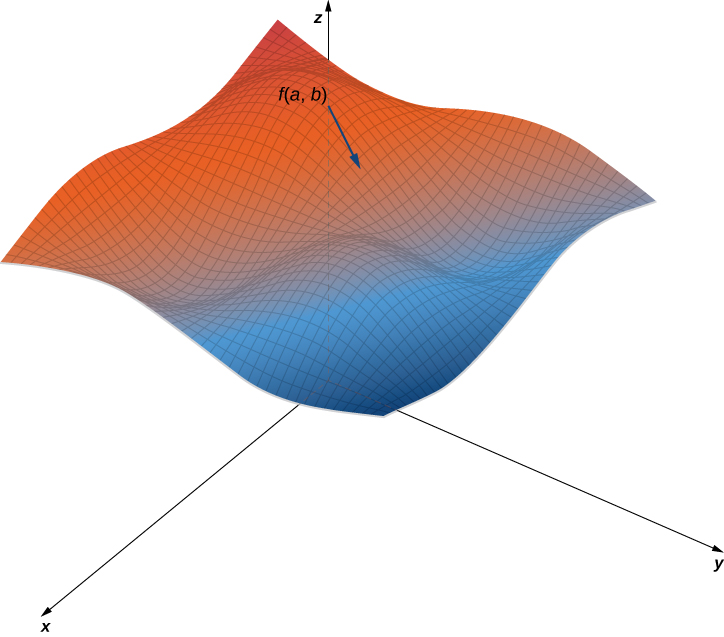
La figure\(\PageIndex{5}\) montre une partie du graphique de la fonction\(f(x,y)=3+\sin x \sin y\). Étant donné un point\((a,b)\) dans le domaine de\(f\), la valeur maximale de la dérivée directionnelle à ce point est donnée par\(\|\vecs ∇f(a,b)\|\). Cela équivaudrait au taux de plus grande ascension si la surface représentait une carte topographique. Si nous allions dans la direction opposée, ce serait le taux de descente le plus élevé.
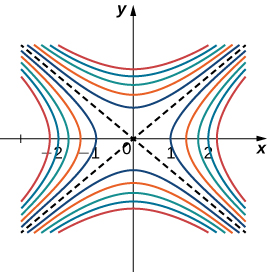
Lorsque vous utilisez une carte topographique, la pente la plus raide se situe toujours dans la direction où les lignes de contour sont les plus proches les unes des autres (Figure\(\PageIndex{6}\)). Ceci est analogue à la carte de contour d'une fonction, en supposant que les courbes de niveau sont obtenues pour des valeurs également espacées sur toute la plage de cette fonction.
Dégradés et courbes de niveau
Rappelez-vous que si une courbe est définie de manière paramétrique par la paire\((x(t),y(t)),\) de fonctions, le vecteur\(x′(t)\,\hat{\mathbf i}+y′(t)\,\hat{\mathbf j}\) est tangent à la courbe pour chaque valeur du\(t\) domaine. Supposons maintenant que c'\(z=f(x,y)\)est une fonction dérivable de\(x\) et\(y\), et qu'elle\((x_0,y_0)\) fait partie de son domaine. Supposons en outre cela\(x_0=x(t_0)\) et\(y_0=y(t_0)\) pour une certaine valeur de\(t\), et considérons la courbe de niveau\(f(x,y)=k\). Définissez\(g(t)=f(x(t),y(t))\) et calculez\(g′(t)\) sur la courbe de niveau. Par la chaîne Rule,
\[g′(t)=f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t). \nonumber \]
Mais\(g′(t)=0\) parce que\(g(t)=k\) pour tous\(t\). Par conséquent, d'une part,
\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=0; \nonumber \]
d'autre part,
\[f_x(x(t),y(t))x′(t)+f_y(x(t),y(t))y′(t)=\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩. \nonumber \]
Par conséquent,
\[\vecs ∇f(x,y)⋅⟨x′(t),y′(t)⟩=0. \nonumber \]
Ainsi, le produit scalaire de ces vecteurs est égal à zéro, ce qui implique qu'ils sont orthogonaux. Cependant, le second vecteur est tangent à la courbe de niveau, ce qui implique que le gradient doit être normal à la courbe de niveau, ce qui donne lieu au théorème suivant.
Supposons que la fonction\(z=f(x,y)\) possède des dérivées partielles continues du premier ordre dans un disque ouvert centré sur un point\((x_0,y_0)\). Si\(\vecs ∇f(x_0,y_0)≠0\), alors\(\vecs ∇f(x_0,y_0)\) est normal à la courbe de\(f\) niveau de\((x_0,y_0).\)
Nous pouvons utiliser ce théorème pour trouver des vecteurs tangents et normaux pour niveler les courbes d'une fonction.
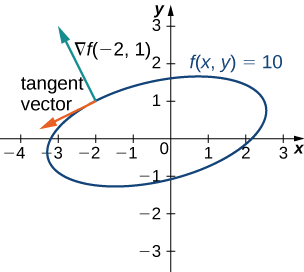
Pour la fonction,\(f(x,y)=2x^2−3xy+8y^2+2x−4y+4,\) trouvez un vecteur tangent à la courbe de niveau au point\((−2,1)\). Tracez la courbe de niveau correspondant à un vecteur tangent\(f(x,y)=18\)\(\vecs ∇f(−2,1)\) et dessinez-le.
Solution
Tout d'abord, nous devons calculer\(\vecs ∇f(x,y):\)
\[f_x(x,y)=4x−3y+2 \;\text{and}\; f_y=−3x+16y−4 \;\text{so}\; \vecs ∇f(x,y)=(4x−3y+2)\,\hat{\mathbf i}+(−3x+16y−4)\,\hat{\mathbf j}.\nonumber \]
Ensuite, nous évaluons\(\vecs ∇f(x,y)\) à\((−2,1):\)
\[\vecs ∇f(−2,1)=(4(−2)−3(1)+2)\,\hat{\mathbf i}+(−3(−2)+16(1)−4)\,\hat{\mathbf j}=−9\,\hat{\mathbf i}+18\,\hat{\mathbf j}.\nonumber \]
Ce vecteur est orthogonal à la courbe au point\((−2,1)\). Nous pouvons obtenir un vecteur tangent en inversant les composantes et en multipliant l'une ou l'autre par\(−1\). Ainsi, par exemple,\(−18\,\hat{\mathbf i}−9\,\hat{\mathbf j}\) est un vecteur tangent (Figure\(\PageIndex{7}\)).
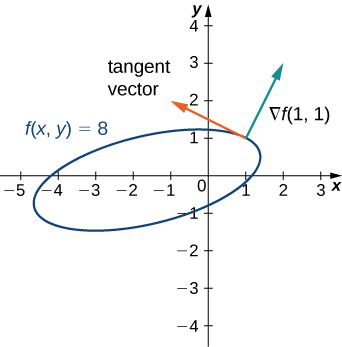
Pour la fonction\(f(x,y)=x^2−2xy+5y^2+3x−2y+3\), trouvez la tangente à la courbe de niveau au point\((1,1)\). Tracez le graphique de la courbe de niveau correspondant à\(f(x,y)=8\)\(\vecs ∇f(1,1)\) et dessinez un vecteur tangent.
- Allusion
-
Calculez le gradient au point\((1,1)\).
- Réponse
-
\(\vecs ∇f(x,y)=(2x−2y+3)\,\hat{\mathbf i}+(−2x+10y−2)\,\hat{\mathbf j}\)
\(\vecs ∇f(1,1)=3\,\hat{\mathbf i}+6\,\hat{\mathbf j}\)
Vecteur tangent :\(6\,\hat{\mathbf i}−3\,\hat{\mathbf j}\) ou\(−6\,\hat{\mathbf i}+3\,\hat{\mathbf j}\)
Gradients tridimensionnels et dérivées directionnelles
La définition d'un gradient peut être étendue aux fonctions de plus de deux variables.
\(w=f(x, y, z)\)Soyons une fonction de trois variables telles que\(f_x, \, f_y\),
\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}.\label{grad3d} \]
\(\vecs ∇f(x,y,z)\)peut également être écrit en tant que diplômé\(f(x,y,z).\)
Le calcul du gradient d'une fonction en trois variables est très similaire au calcul du gradient d'une fonction en deux variables. Nous calculons d'abord les dérivées partielles\(f_z\),\(f_x, \, f_y,\) puis nous utilisons l'équation \ ref {grad3d}.
Trouvez le dégradé\(\vecs ∇f(x,y,z)\) de chacune des fonctions suivantes :
- \(f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz\)
- \(f(x,y,z)=e^{−2z}\sin 2x \cos 2y\)
Solution
Pour les deux parties a. et b., nous calculons d'abord les dérivées partielles\(f_z\),\(f_x,f_y,\) puis nous utilisons l'équation \ ref {grad3d}.
a.\(f_x(x,y,z)=10x−2y+3z\),\(f_y(x,y,z)=−2x+2y−4z\)\( f_z(x,y,z)=3x−4y+2z\), et donc
\ [\ begin {align*} \ vecs f (x, y, z) &=f_x (x, y, z) \, \ hat {\ mathbf i} +f_y (x, y, z) \, \ hat {\ mathbf j} +f_z (x, y, z) \, \ hat {\ mathbf k} \ \ & =( 10x−z) \, \ hat {\ mathbf k} \ \
& =( 10x−z) 2y+3z) \, \ hat {\ mathbf i} + (−2x+2y−4z) \, \ hat {\ mathbf j} + (3x-4y+2z) \, \ hat {\ mathbf k}. \ end {align*} \]
b.\(f_x(x,y,z) =2e^{−2z}\cos 2x \cos 2y\),\( f_y(x,y,z)=−2e^{−2z} \sin 2x \sin 2y\)\(f_z(x,y,z)=−2e^{−2z}\sin 2x \cos 2y\), et donc
\[\begin{align*} \vecs ∇f(x,y,z) &=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k} \\ &=(2e^{−2z}\cos 2x \cos 2y)\,\hat{\mathbf i}+(−2e^{−2z} \sin 2x \sin 2y)\,\hat{\mathbf j}+(−2e^{−2z}\sin 2x \cos 2y)\,\hat{\mathbf k} \\ &=2e^{−2z}(\cos 2x \cos 2y \,\hat{\mathbf i}−\sin 2x \sin 2y\,\hat{\mathbf j}−\sin 2x \cos 2y\,\hat{\mathbf k}). \end{align*}\]
Trouvez le dégradé\(\vecs ∇f(x,y,z)\) de\(f(x,y,z)=\dfrac{x^2−3y^2+z^2}{2x+y−4z.}\)
- Réponse
-
\[\vecs ∇f(x,y,z)=\dfrac{2x^2+2xy+6y^2−8xz−2z^2}{(2x+y−4z)^2}\,\hat{\mathbf i}−\dfrac{x^2+12xy+3y^2−24yz+z^2}{(2x+y−4z)^2}\,\hat{\mathbf j}+\dfrac{4x^2−12y^2−4z^2+4xz+2yz}{(2x+y−4z)^2}\,\hat{\mathbf k}\nonumber \]
La dérivée directionnelle peut également être généralisée aux fonctions de trois variables. Pour déterminer une direction en trois dimensions, un vecteur à trois composantes est nécessaire. Ce vecteur est un vecteur unitaire et les composants du vecteur unitaire sont appelés cosinus directionnels. Étant donné un vecteur\(\vecs u\) unitaire tridimensionnel sous forme standard (c'est-à-dire que le point initial se trouve à l'origine), ce vecteur forme trois angles différents avec les\(z\) axes positifs\(x\)\(y\) -, - et -. Appelons ces angles\(α,β,\) et\(γ\). Ensuite, les cosinus directionnels sont donnés par\(\cos α,\cos β,\) et\(\cos γ\). Ce sont les composantes du vecteur unitaire\(\vecs u\) ; puisqu'il\(\vecs u\) s'agit d'un vecteur unitaire, il est vrai que\(\cos^2 α+\cos^2 β+\cos^2 γ=1.\)
\(w=f(x,y,z)\)Suppose est une fonction de trois variables avec un domaine de\(D\). Soit\((x_0,y_0,z_0)∈D\) et\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) soit un vecteur unitaire. Ensuite, la dérivée directionnelle de\(f\) dans la direction de\(u\) est donnée par
\[D_{\vecs u}f(x_0,y_0,z_0)=\lim_{t→0}\dfrac{f(x_0+t \cos α,y_0+t\cos β,z_0+t\cos γ)−f(x_0,y_0,z_0)}{t} \nonumber \]
à condition que la limite existe.
Nous pouvons calculer la dérivée directionnelle d'une fonction de trois variables en utilisant le gradient, ce qui conduit à une formule analogue à l'équation \ ref {DD2v}.
\(f(x,y,z)\)Soit une fonction dérivable de trois variables et\(\vecs u=\cos α\,\hat{\mathbf i}+\cos β\,\hat{\mathbf j}+\cos γ\,\hat{\mathbf k}\) soit un vecteur unitaire. Ensuite, la dérivée directionnelle de\(f\) dans la direction de\(\vecs u\) est donnée par
\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_z(x,y,z)\cos γ. \label{DDv3} \]
Les trois angles\(α,β,\) et\(γ\) déterminez le vecteur unitaire\(\vecs u\). En pratique, nous pouvons utiliser un vecteur arbitraire (non unitaire), puis le diviser par sa magnitude pour obtenir un vecteur unitaire dans la direction souhaitée.
Calculer\(D_{\vecs v}f(1,−2,3)\) dans le sens de\(\vecs v=−\,\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}\) pour la fonction
\[ f(x,y,z)=5x^2−2xy+y^2−4yz+z^2+3xz. \nonumber \]
Solution :
Tout d'abord, nous trouvons l'ampleur de\(v\) :
\[‖\vecs v‖=\sqrt{(−1)^2+(2)^2+(2)^2}=\sqrt{9}=3. \nonumber \]
Par conséquent,\(\dfrac{\vecs v}{‖\vecs v‖}=\dfrac{−\hat{\mathbf i}+2\,\hat{\mathbf j}+2\,\hat{\mathbf k}}{3}=−\dfrac{1}{3}\,\hat{\mathbf i}+\dfrac{2}{3}\,\hat{\mathbf j}+\dfrac{2}{3}\,\hat{\mathbf k}\) est un vecteur unitaire dans la direction de\(\vecs v\), donc\(\cos α=−\dfrac{1}{3},\cos β=\dfrac{2}{3},\) et\(\cos γ=\dfrac{2}{3}\). Ensuite, nous calculons les dérivées partielles de\(f\) :
\ [\ begin {align*} f_x (x, y, z) &=10x−2y+3z \ \
f_y (x, y, z) &=−2x+2y−4z \ \
f_z (x, y, z) &=−4y+2z+3x, \ end {align*} \ aucun numéro \]
puis remplacez-les dans l'équation \ ref {DDv3} :
\ [\ begin {align*} D_ {\ vecs v} f (x, y, z) &=f_x (x, y, z) \ cos α+f_y (x, y, z) \ cos β+f_z (x, y, z) \ cos γ \ \
& =( 10x−2y+3z) (+ \ dfrac {1} {3}) (−2x+2y−4z) (\ dfrac {2} {3}) + (−4 ans+2z+3x) (\ dfrac {2} {3}) \ \
&=− \ dfrac {10x} {3} + \ dfrac {2} {3} − \ dfrac {3z} {3} − \ dfrac {4x} {3} + \ dfrac {4y} {3} − \ dfrac {8z} {3} − \ dfrac { 8y} {3} + \ dfrac {4z} {3} + \ dfrac {6x} {3} \ \
&=− \ dfrac {8x} {3} − \ dfrac {2y} {3} − \ dfrac {7z} {3}. \ end {align*} \]
Enfin, pour trouver un\(D_{\vecs v}f(1,−2,3),\) substitut\(x=1,\, y=−2\), et\(z=3:\)
\ [\ begin {align*} D_ {\ vecs v} f (1, −2,3) &=− \ dfrac {8 (1)} {3} − \ dfrac {2 (−2)} {3} − \ dfrac {7 (3)} {3} \ \
&=− \ dfrac {8} {3} + \ dfrac {4} {3} − \ dfrac {21} {3} \ \
&=− \ dfrac {25} {3}. \ end {align*} \]
Calculer\(D_{\vecs v}f(x,y,z)\) et\(D_{\vecs v}f(0,−2,5)\) dans le sens de\(\vecs v=−3\,\hat{\mathbf i}+12\,\hat{\mathbf j}−4\,\hat{\mathbf k}\) pour la fonction
\[f(x,y,z)=3x^2+xy−2y^2+4yz−z^2+2xz.\nonumber \]
- Allusion
-
Divisez d'abord\(\vecs v\) par sa magnitude, calculez les dérivées partielles de\(f\), puis utilisez l'équation \ ref {DDv3}.
- Réponse
-
\(D_{\vecs v}f(x,y,z)=−\dfrac{3}{13}(6x+y+2z)+\dfrac{12}{13}(x−4y+4z)−\dfrac{4}{13}(2x+4y−2z)\)
\(D_{\vecs v}f(0,−2,5)=\dfrac{384}{13}\)
Résumé
- Une dérivée directionnelle représente le taux de variation d'une fonction dans une direction donnée.
- Le gradient peut être utilisé dans une formule pour calculer la dérivée directionnelle.
- Le gradient indique la direction de la plus grande variation d'une fonction de plusieurs variables.
Équations clés
- dérivée directionnelle (deux dimensions)\[D_{\vecs u}f(a,b)=\lim_{h→0}\dfrac{f(a+h\cos θ,b+h\sin θ)−f(a,b)}{h} \nonumber \] ou\[D_{\vecs u}f(x,y)=f_x(x,y)\cos θ+f_y(x,y)\sin θ\nonumber \]
- dégradé (deux dimensions)\[\vecs ∇f(x,y)=f_x(x,y)\,\hat{\mathbf i}+f_y(x,y)\,\hat{\mathbf j}\nonumber \]
- dégradé (trois dimensions)\[\vecs ∇f(x,y,z)=f_x(x,y,z)\,\hat{\mathbf i}+f_y(x,y,z)\,\hat{\mathbf j}+f_z(x,y,z)\,\hat{\mathbf k}\nonumber \]
- dérivée directionnelle (trois dimensions)\[D_{\vecs u}f(x,y,z)=\vecs ∇f(x,y,z)⋅\vecs u=f_x(x,y,z)\cos α+f_y(x,y,z)\cos β+f_x(x,y,z)\cos γ\nonumber \]
Lexique
- dérivée directionnelle
-
la dérivée d'une fonction dans la direction d'un vecteur unitaire donné
- dégradé
-
le gradient de la fonction\(f(x,y)\) est défini comme étant\(\vecs ∇f(x,y)=(∂f/∂x)\,\hat{\mathbf i}+(∂f/∂y)\,\hat{\mathbf j},\) susceptible d'être généralisé à une fonction comportant un nombre quelconque de variables indépendantes


