Skip to main content
Global

14.6E : Exercices pour la section 14.6

  1. Last updated
  2. Save as PDF
  • Page ID
    197334

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans l'exercice 1, trouvez la dérivée directionnelle en utilisant uniquement la définition de limite.

    1) a.\( f(x,y)=5−2x^2−\frac{1}{2}y^2\) à un point situé\( P(3,4)\) dans la direction de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Réponse
    un.\( D_{\vecs u}f(3,4) =−8\sqrt{2}\)

    1) b.\( f(x,y)=y^2\cos(2x)\) au point situé\( P(\frac{π}{3},2)\) dans la direction de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Réponse
    b.\( D_{\vecs u}f(\frac{π}{3},2) =−2\sqrt{6}-\sqrt{2}\)

    2) Trouvez la dérivée directionnelle d'\( f(x,y)=y^2\sin(2x)\)au point\( P(\frac{π}{4},2)\) dans la direction de\(\vecs u=5\,\hat{\mathbf i}+12\,\hat{\mathbf j}\).

    Dans les exercices 3 à 13, trouvez la dérivée directionnelle de la fonction dans la direction de\(\vecs v\) en fonction de\(x\) et\(y\). N'oubliez pas que vous devez d'abord trouver un vecteur unitaire dans la direction du vecteur de direction. Trouvez ensuite la valeur de la dérivée directionnelle au point\(P\).

    3)\( f(x,y)=xy, \quad P(-2,0), \quad \vecs v=\frac{1}{2}\,\hat{\mathbf i}+\frac{\sqrt{3}}{2}\,\hat{\mathbf j}\)

    Réponse
    \(D_{\vecs v}f(x, y) = \frac{1}{2}y + \frac{\sqrt{3}}{2}x \)
    \(D_{\vecs v}f(-2, 0) = −\sqrt{3}\)

    4)\( h(x,y)=e^x\sin y,\quad P(1,\frac{π}{2}),\quad \vecs v=−\,\hat{\mathbf i}\)

    5)\( f(x,y)=x^2y,\quad P(−5,5),\quad \vecs v=3\,\hat{\mathbf i}−4\,\hat{\mathbf j}\)

    Réponse
    \(D_{\vecs v}f(x, y) = \frac{6}{5}xy - \frac{4}{5}x^2 \)
    \(D_{\vecs v}f(-5,5)= -50\)

    6)\( f(x,y)=xy,\quad P(1,1), \quad \vecs u=⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\)

    7)\( f(x,y)=x^2−y^2, \quad P(1,0), \quad \vecs u=⟨\frac{\sqrt{3}}{2},\frac{1}{2}⟩\)

    Réponse
    \(D_{\vecs u}f(x, y) = x\sqrt{3} - y \)
    \(D_{\vecs u}f(1,0)= \sqrt{3}\)

    8)\( f(x,y)=3x+4y+7,\quad P(0,\frac{π}{2}), \quad \vecs u=⟨\frac{3}{5},\frac{4}{5}⟩\)

    9)\( f(x,y)=e^x\cos y,\quad P=(0,\frac{π}{2}), \quad \vecs u=⟨0,5⟩\)

    Réponse
    \(D_{\vecs u}f(x, y) = -e^x\sin y \)
    \(D_{\vecs u}f(0, \frac{π}{2})= −1\)

    10)\( f(x,y)=y^{10},\quad \vecs u=⟨0,−3⟩,\quad P=(1,−1)\)

    11)\( f(x,y)=\ln(x^2+y^2),\quad \vecs u=⟨2,-5⟩,\quad P(1,2)\)

    Réponse
    \(D_{\vecs u}f(x, y) = \frac{\sqrt{29}}{29}\left( \dfrac{4x-10y}{x^2 +y^2}\right) \)
    \(D_{\vecs u}f(1,2)= -\frac{16\sqrt{29}}{145}\)

    (12)\( h(x,y,z)=xyz, \quad P(2,1,1),\quad \vecs v=2\,\hat{\mathbf i}+\,\hat{\mathbf j}−\,\hat{\mathbf k}\)

    Réponse
    \( D_{\vecs v}h(x, y, z) = \frac{\sqrt{6}}{6}(2yz + xz - xy)\)
    \( D_{\vecs v}h(2,1,1) = \frac{2}{\sqrt{6}} = \frac{\sqrt{6}}{3}\)

    13)\( f(x,y,z)=y^2+xz,\quad P(1,2,2),\quad \vecs v=⟨2,−1,2⟩\)

    Réponse
    \( D_{\vecs v}f(x, y, z) = \frac{2}{3}(z - y + x)\)
    \(D_{\vecs v}f(1,2,2)= \frac{2}{3}\)

    Dans les exercices 14 à 19, trouvez la dérivée directionnelle de la fonction dans la direction du vecteur unitaire\(\vecs u=\cos θ \,\hat{\mathbf i}+\sin θ \,\hat{\mathbf j}.\)

    (14)\( f(x,y)=x^2+2y^2,\quad θ=\frac{π}{6}\)

    (15)\( f(x,y)=\dfrac{y}{x+2y},\quad θ=−\frac{π}{4}\)

    Réponse
    \( D_{\vecs u}f(x,y) = \dfrac{−\sqrt{2}(x+y)}{2(x+2y)^2}\)

    16)\( f(x,y)=\cos(3x+y),\quad θ=\frac{π}{4}\)

    17)\( w(x,y)=ye^x,\quad θ=\frac{π}{3}\)

    Réponse
    \( D_{\vecs u}f(x,y) = \dfrac{e^x(y+\sqrt{3})}{2}\)

    18)\( f(x,y)=x\arctan(y),\quad θ=\frac{π}{2}\)

    19)\( f(x,y)=\ln(x+2y),\quad θ=\frac{π}{3}\)

    Réponse
    \( D_{\vecs u}f(x,y) = \dfrac{1+2\sqrt{3}}{2(x+2y)}\)

    Dans les exercices 20 à 23, trouvez le dégradé\(\vecs \nabla f\).

    20) Trouvez le dégradé de\( f(x, y) = 3x^2 + y^3 - 3x + y\). Ensuite, trouvez sa valeur au point\(P(2,3)\).

    21) Trouvez le dégradé de\( f(x,y)=\dfrac{14−x^2−y^2}{3}\). Ensuite, trouvez le dégradé au point\( P(1,2)\).

    Réponse
    \( \vecs \nabla f(x, y) = -\frac{2}{3}x\,\hat{\mathbf i} -\frac{2}{3}y\,\hat{\mathbf j}\)
    \( \vecs \nabla f(1,2) = -\frac{2}{3}\,\hat{\mathbf i} -\frac{4}{3}\,\hat{\mathbf j}\)

    22) Déterminez le dégradé de\( f(x,y)=\ln(4x^3 - 3y)\). Ensuite, trouvez le dégradé au point\( P(1,1)\).

    23) Déterminez le dégradé de\( f(x,y,z)=xy+yz+xz\). Trouvez ensuite le dégradé au point\( P(1,2,3).\)

    Réponse
    \( \vecs \nabla f(x, y, z) = ⟨y+z, x+z, y + x⟩\)
    \( \vecs \nabla f(1,2,3) = ⟨5,4,3⟩\)

    Dans les exercices 24 à 25, trouvez la dérivée directionnelle de la fonction au point\( P\) situé dans la direction de\( Q\).

    (24)\( f(x,y)=x^2+3y^2,\quad P(1,1),\quad Q(4,5)\)

    25)\( f(x,y,z)=\dfrac{y}{x+z},\quad P(2,1,−1),\quad Q(−1,2,0)\)

    Réponse
    \( D_{\vecd{PQ}}f(x,y) = \frac{3}{\sqrt{11}}\)

    26) Déterminez la dérivée directionnelle de\( f(x,y,z))\) at\( P\) et dans la direction de\( \vecs u: \quad f(x,y,z)=\ln(x^2+2y^2+3z^2),\quad P(2,1,4),\quad \vecs u=\frac{−3}{13}\,\hat{\mathbf i}−\frac{4}{13}\,\hat{\mathbf j}−\frac{12}{13}\,\hat{\mathbf k}\).

    Dans les exercices 27 à 29, trouvez la dérivée directionnelle de la fonction\( P\) dans la direction de\(\vecs u\).

    (27)\( f(x,y)=\ln(5x+4y),\quad P(3,9),\quad \vecs u=6\,\hat{\mathbf i}+8\,\hat{\mathbf j}\)

    Réponse
    \( D_{\vecs u}f(3,9) = \frac{31}{255}\)

    (28)\( f(x,y)=−7x+2y,\quad P(2,−4),\quad \vecs u=4\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    (29)\( f(x,y,z)=4x^5y^2z^3,\quad P(2,−1,1),\quad \vecs u=\frac{1}{3}\,\hat{\mathbf i}+\frac{2}{3}\,\hat{\mathbf j}−\frac{2}{3}\,\hat{\mathbf k}\)

    Réponse
    \( D_{\vecs u}f(2,-1,1) = -320\)

    30) [T] Utilisez la technologie pour esquisser la courbe de niveau\( f(x,y)=4x−2y+3\) qui passe\( P(1,2)\) et dessiner le vecteur de gradient auquel\( P\).

    31) [T] Utilisez la technologie pour esquisser la courbe de niveau\( f(x,y)=x^2+4y^2\) qui passe\( P(−2,0)\) et dessiner le vecteur de gradient auquel\(P\).

    Réponse
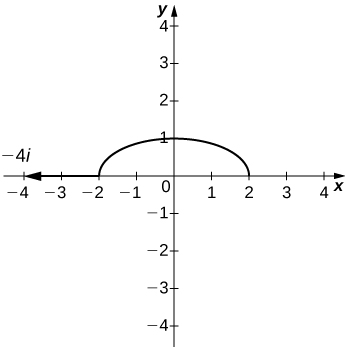
    Esquisse de la courbe de niveau de f (x, y) =x^2+4y^2 qui passe par P (−2,0) et montrant le vecteur de gradient en P.

    Dans les exercices 32 à 35, trouvez le vecteur de dégradé au point indiqué.

    32)\( f(x,y)=xy^2−yx^2,\quad P(−1,1)\)

    33)\( f(x,y)=xe^y−\ln(x),\quad P(−3,0)\)

    Réponse
    \(\vecs \nabla f(-3,0) = \frac{4}{3}\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    34)\( f(x,y,z)=xy−\ln(z),\quad P(2,−2,2)\)

    35)\( f(x,y,z)=x\sqrt{y^2+z^2}, \quad P(−2,−1,−1)\)

    Réponse
    \(\vecs \nabla f(-2,-1,-1) = \sqrt{2}\,\hat{\mathbf i}+\sqrt{2}\,\hat{\mathbf j}+\sqrt{2}\,\hat{\mathbf k}\)

    Dans les exercices 36 à 40, trouvez la dérivée directionnelle indiquée de la fonction.

    36)\( f(x,y)=x^2+xy+y^2\) au point\( (−5,−4)\) dans la direction où la fonction augmente le plus rapidement.

    37)\( f(x,y)=e^{xy}\) au point\( (6,7)\) dans la direction où la fonction augmente le plus rapidement.

    Réponse
    \( 1.6(10^{19})\)

    38)\( f(x,y)=\arctan\left(\dfrac{y}{x}\right)\) au point\( (−9,9)\) dans la direction où la fonction augmente le plus rapidement.

    39)\( f(x,y,z)=\ln(xy+yz+zx)\) au point\( (−9,−18,−27)\) dans la direction où la fonction augmente le plus rapidement.

    Réponse
    \( \frac{5\sqrt{2}}{99}\)

    40)\( f(x,y,z)=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\) au point\( (5,−5,5)\) dans la direction où la fonction augmente le plus rapidement.

    Dans les exercices 41 à 43, déterminez le taux de variation maximal d'\( f\)un point donné et la direction dans laquelle il se produit.

    41)\( f(x,y)=xe^{−y}, \quad (-2,0)\)

    Réponse
    \(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \sqrt{5}, \quad ⟨1,2⟩\)
    Solution :
    \( \vecs \nabla f(x, y) = e^{-y} \mathbf{\hat i} - xe^{-y} \mathbf{\hat j}.\)Donc,\(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \|\vecs \nabla f(-2, 0)\| = \sqrt{5}.\)
    la direction dans laquelle cela se produira sera juste la direction du vecteur de dégradé :\(\vecs \nabla f(-2, 0) = ⟨1,2⟩.\)

    (42)\( f(x,y)=\sqrt{x^2+2y}, \quad (4,10)\)

    43)\( f(x,y)=\cos(3x+2y),\quad (\frac{π}{6},−\frac{π}{8})\)

    Réponse
    \( \text{max}\big\{D_{\vecs u} f\left(\frac{π}{6},−\frac{π}{8}\right)\big\} = \sqrt{\frac{13}{2}} = \frac{\sqrt{26}}{2},\quad ⟨−3,−2⟩\)

    Dans les exercices 44 à 47, trouvez les équations de

    a. le plan tangent et

    b. la ligne normale vers la surface donnée au point donné.

    44) La courbe de\( f(x,y,z)=4x^2−2y^2+z^2\) niveau\( f(x,y,z)=12\) pour le point\( (2,2,2).\)

    45)\( f(x,y,z)=xy+yz+xz=3\) au point\( (1,1,1)\)

    Réponse
    a. équation du plan tangent :\(x+y+z=3\),
    b. équations droites normales :\(x−1=y−1=z−1\)

    46)\( f(x,y,z)=xyz=6\) au point\( (1,2,3)\)

    47)\( f(x,y,z)=xe^y\cos z−z=1\) au point\( (1,0,0)\)

    Réponse
    a. équation du plan tangent :\(x+y−z=1\),
    b. équations droites normales :\(x−1=y=−z\)

    Dans les exercices 48 à 51, résolvez le problème indiqué.

    48) La température\( T\) dans une sphère métallique est inversement proportionnelle à la distance depuis le centre de la sphère (origine :\( (0,0,0))\). La température au point\( (1,2,2)\) est de\( 120\) °C.

    a. Déterminez le taux de variation de la température à un point\( (1,2,2)\) situé dans la direction du point\( (2,1,3).\)

    b. Montrez qu'en tout point de la sphère, la direction de la plus forte augmentation de température est donnée par un vecteur pointant vers l'origine.

    49) Le potentiel électrique (tension) dans une certaine région de l'espace est donné par la fonction\( V(x,y,z)=5x^2−3xy+xyz.\)

    a. Détermine le taux de variation de la tension à un point\( (3,4,5)\) situé dans la direction du vecteur\( ⟨1,1,−1⟩.\)

    b. Dans quelle direction la tension change-t-elle le plus rapidement au point\( (3,4,5)\) ?

    c. Quel est le taux de variation maximal de la tension au point\( (3,4,5)\) ?

    Réponse
    a.\(\frac{32}{\sqrt{3}}\),
    b.\(⟨38,6,12⟩\),
    c.\(2\sqrt{406}\)

    50) Si le potentiel électrique\( (x,y)\) en un point du\(xy\) plan est\( V(x,y)=e^{−2x}\cos(2y)\), alors le vecteur d'intensité électrique à\( (x,y)\) est\( E=−\vecs \nabla V(x,y).\)

    a. Trouvez le vecteur d'intensité électrique à\( (\frac{π}{4},0).\)

    b. Montrez qu'en chaque point du plan, le potentiel électrique diminue le plus rapidement dans la direction du vecteur\( E.\)

    51) En deux dimensions, le mouvement d'un fluide idéal est régi par un potentiel de vitesse\( φ\). Les composantes de vitesse du fluide\(u\) dans la direction\(x\) - et\(v\) dans la\(y\) direction - sont données par\( ⟨u,v⟩=\vecs \nabla φ\). Trouvez les composantes de vitesse associées au potentiel de vitesse\( φ(x,y)=\sin πx\sin 2πy.\)

    Réponse
    \( ⟨u,v⟩=⟨π\cos(πx)\sin(2πy),2π\sin(πx)\cos(2πy)⟩\)

    Contributeurs