14.5E : Exercices pour la section 14.5

Last updated
Save as PDF

Page ID: 197359

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 6, utilisez les informations fournies pour résoudre le problème.

1) Laissez$ w(x,y,z)=xy\cos z,$ où$ x=t,y=t^2,$ et$ z=\arcsin t.$ trouvez$ \dfrac{dw}{dt}$.

Réponse: $ \dfrac{dw}{dt}=y\cos z+x\cos z(2t)−\dfrac{xy\sin z}{\sqrt{1−t^2}}$

2) Laissez$ w(t,v)=e^{tv}$ où$ t=r+s$ et$ v=rs$. Trouvez$ \dfrac{∂w}{∂r}$ et$ \dfrac{∂w}{∂s}$.

3) Si$ w=5x^2+2y^2, \quad x=−3u+v,$ et$ y=u−4v,$ trouvez$ \dfrac{∂w}{∂u}$ et$ \dfrac{∂w}{∂v}$.

Réponse: $ \dfrac{∂w}{∂u}=−30x+4y \quad\ = \quad -30(-3u + v) + 4(u - 4v) \quad = \quad 90u -30v + 4u - 16v \quad = \quad 94u - 46v$,
$\dfrac{∂w}{∂v}=10x−16y \quad\ = \quad 10(-3u + v) - 16(u - 4v) \quad = \quad -30u +10v - 16u + 64v \quad = \quad -46u + 74v$

4) Si$ w=xy^2,x=5\cos(2t),$ et$ y=5\sin(2t)$, trouvez$ \dfrac{∂w}{∂t}$.

5) Si$ f(x,y)=xy,x=r\cos θ,$ oui$ y=r\sin θ$, trouvez$\dfrac{∂f}{∂r}$ et exprimez la réponse en termes de$ r$ et$ θ$.

Réponse: $ \dfrac{∂f}{∂r}=r\sin(2θ)$

6) Supposons$ f(x,y)=x+y,u=e^x\sin y,\quad x=t^2$ et$ y=πt$, où$ x=r\cos θ$ et$ y=r\sin θ$. Trouve$ \dfrac{∂f}{∂θ}$.

Dans les exercices 7 à 12, trouvez de deux$ \dfrac{dz}{dt}$ manières, d'abord en utilisant la règle de la chaîne, puis par substitution directe.

7)$ z=x^2+y^2, \quad x=t,y=t^2$

Réponse: $ \dfrac{dz}{dt}=2t+4t^3$

8)$ z=\sqrt{x^2+y^2},\quad y=t^2,x=t$

9)$ z=xy,\quad x=1−\sqrt{t},y=1+\sqrt{t}$

Réponse: $ \dfrac{dz}{dt}=−1$

10)$ z=\frac{x}{y},\quad x=e^t,y=2e^t$

11)$ z=\ln(x+y), \quad x=e^t,y=e^t$

Réponse: $ \dfrac{dz}{dt}=1$

(12)$ z=x^4,\quad x=t,y=t$

13) Laissez$ w(x,y,z)=x^2+y^2+z^2, \quad x=cost,y=sint,$ et$ z=e^t$. Exprimez$ w$ en fonction de$ t$ et trouvez$ \dfrac{dw}{dt}$ directement. Ensuite, recherchez$ \dfrac{dw}{dt}$ en utilisant la règle de chaîne.

Réponse: $ \dfrac{dw}{dt}=2e^{2t}$dans les deux cas

14) Laissez$ z=x^2y,$ où$ x=t^2$ et$ y=t^3$. Trouve$ \dfrac{dz}{dt}$.

15) Laissez$ u=e^x\sin y,$ où$ x=-\ln 2t$ et$ y=πt$. Trouvez$ \dfrac{du}{dt}$ quand$ x=\ln 2$ et$ y=\frac{π}{4}$.

Réponse: $ \dfrac{du}{dt} = \sqrt{2}\big(\pi - 4\big)$

Dans les exercices 16 à 33, trouvez des$ \dfrac{dy}{dx}$ dérivées partielles.

16)$ \sin(6x)+\tan(8y)+5=0$

17)$ x^3+y^2x−3=0$

Réponse: $ \dfrac{dy}{dx}=−\dfrac{3x^2+y^2}{2xy}$

18)$ \sin(x+y)+\cos(x−y)=4$

19)$ x^2−2xy+y^4=4$

Réponse: $ \dfrac{dy}{dx}=\dfrac{y−x}{−x+2y^3}$

(20)$ xe^y+ye^x−2x^2y=0$

(21)$ x^{2/3}+y^{2/3}=a^{2/3}$

Réponse: $ \dfrac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}$

(22)$ x\cos(xy)+y\cos x=2$

23)$ e^{xy}+ye^y=1$

Réponse: $ \dfrac{dy}{dx}=−\dfrac{ye^{xy}}{xe^{xy}+e^y(1+y)}$

(24)$ x^2y^3+\cos y=0$

25) Trouvez$ \dfrac{dz}{dt}$ en utilisant la règle de chaîne où$ z=3x^2y^3,\,\,x=t^4,$ et$ y=t^2$.

Réponse: $ \dfrac{dz}{dt}=42t^{13}$

26) Laisse$ z=3\cos x−\sin(xy),x=\frac{1}{t},$ et$ y=3t.$ trouve$ \dfrac{dz}{dt}$.

27) Laissez$ z=e^{1−xy},\,\, x=t^{1/3},$ et$ y=t^3$. Trouve$ \dfrac{dz}{dt}$.

Réponse: $ \dfrac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}$

28) Trouvez$ \dfrac{dz}{dt}$ selon la règle de la chaîne où$ z=\cosh^2(xy),\,\,x=\frac{1}{2}t,$ et$ y=e^t$.

29) Laisse$ z=\dfrac{x}{y},\,\, x=2\cos u,$ et$ y=3\sin v.$ trouve$ \dfrac{∂z}{∂u}$ et$ \dfrac{∂z}{∂v}$.

Réponse: $ \dfrac{∂z}{∂u}=\dfrac{−2\sin u}{3\sin v}$et$ \dfrac{∂z}{∂v}=\dfrac{−2\cos u\cos v}{3\sin^2v}$

30) Laissez$ z=e^{x^2y}$, où$ x=\sqrt{uv}$ et$ y=\frac{1}{v}$. Trouvez$ \dfrac{∂z}{∂u}$ et$ \dfrac{∂z}{∂v}$.

31) Si$ z=xye^{x/y},\,\, x=r\cos θ,$ et$ y=r\sin θ$, trouvez$ \dfrac{∂z}{∂r}$ et$ \dfrac{∂z}{∂θ}$ quand$ r=2$ et$ θ=\frac{π}{6}$.

Réponse: $ \dfrac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \dfrac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}$

32)$ \dfrac{∂w}{∂s}$ Déterminez si$ w=4x+y^2+z^3,\,\,x=e^{rs^2},\,\,y=\ln(\frac{r+s}{t}),$ et$ z=rst^2$.

33) Si$ w=\sin(xyz),\,\,x=1−3t,\,\,y=e^{1−t},$ et$ z=4t$, trouvez$ \dfrac{∂w}{∂t}$.

Réponse: $ \dfrac{∂w}{∂t}=-3yz\cos(xyz)−xze^{1−t}\cos(xyz)+4xy\cos(xyz)$

Dans les exercices 34 à 36, utilisez ces informations : Une fonction$ f(x,y)$ est dite homogène de degré$ n$ si$ f(tx,ty)=t^nf(x,y)$. Pour toutes les fonctions homogènes du degré$ n$, l'équation suivante est vraie :$ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$. Montrez que la fonction donnée est homogène et vérifiez-la$ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$.

34)$ f(x,y)=3x^2+y^2$

35)$ f(x,y)=\sqrt{x^2+y^2}$

Réponse: $ f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \quad \dfrac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)$

36)$ f(x,y)=x^2y−2y^3$

37) Le volume d'un cylindre circulaire droit est donné par$ V(x,y)=πx^2y,$ où$ x$ est le rayon du cylindre et$ y$ la hauteur du cylindre. Supposons$ x$ et$ y$ sont des fonctions de$ t$ données par$ x=\frac{1}{2}t$ et de$ y=\frac{1}{3}t$ telle sorte que$ x$$ y$ les deux augmentent avec le temps. À quelle vitesse le volume augmente-t-il quand$ x=2$ et$ y=5$ ? Supposons que le temps est mesuré en secondes.

Réponse: $ \ddfrac{dV}{dt} = \frac{34π}{3}\,\text{units}^3/\text{s}$

38) La pression$ P$ d'un gaz est liée au volume et à la température par la formule$ PV=kT$, où la température est exprimée en kelvins. Exprime la pression du gaz en fonction à la fois de$ V$ et$ T$. $ \dfrac{dP}{dt}$Détermine quand$ k=1, \dfrac{dV}{dt}=2$ cm ³$ \dfrac{dT}{dt}=12$ /min$ V=20 cm^3$, K/min et$ T=20°F$.

39) Le rayon d'un cône circulaire droit augmente à$ 3$ cm/min tandis que la hauteur du cône diminue à$ 2$ cm/min. Détermine le taux de variation du volume du cône lorsque le rayon est en$ 13$ cm et la hauteur en$ 18$ cm.

Réponse: $ \dfrac{dV}{dt}=\frac{1066π}{3}\,\text{cm}^3/\text{min}$

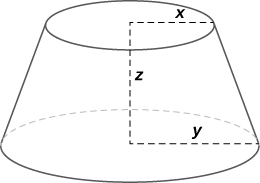
40) Le volume d'un tronc de cône est donné par la formule$ V=\frac{1}{3}πz(x^2+y^2+xy),$ où$ x$ est le rayon du plus petit cercle,$ y$ le rayon du grand cercle et$ z$ la hauteur du tronc (voir figure). Déterminez le taux de variation du volume de ce frustum lorsque vous$ x=10$$y=12$ entrez, entrez et$ z=18$ entrez.

$Frustum d'un cône avec une hauteur z, un rayon supérieur de x et un rayon inférieur de y.$

41) Une boîte fermée a la forme d'un solide rectangulaire aux dimensions$ x,y,$ et$ z$. (Les dimensions sont en pouces.) Supposons que chaque dimension change au rythme de$ 0.5$ l'entrée. /min. Déterminez le taux de variation de la surface totale de la boîte lorsque vous$ x=2$$y=3$ entrez, entrez et$ z=1$ entrez.

Réponse: $ \dfrac{dA}{dt}=12\, \text{in.}^2/\text{min}$

42) La résistance totale dans un circuit qui possède trois résistances individuelles représentées par$ x,y,$ et$ z$ est donnée par la formule$ R(x,y,z)=\dfrac{xyz}{yz+xz+xy}$. Supposons qu'à un moment donné$ 100\,Ω$, la$ y$ résistance soit, que la$ z$ résistance soit$ 200\,Ω,$ et que la$ x$ résistance soit$ 300\,Ω.$ également, supposons que$ 2\,Ω/\text{min},$ la$ y$ résistance change à un rythme où la résistance change au rythme de$ 1\,Ω/\text{min}$, et$ x$ $ z$la résistance ne change pas. Déterminez le taux de variation de la résistance totale dans ce circuit à ce moment.

43) La$ T$ température en un point$ (x,y)$ est$ T(x,y)$ et est mesurée à l'aide de l'échelle Celsius. Une mouche rampe de telle sorte que sa position au bout de$ t$ quelques secondes soit donnée par$ x=\sqrt{1+t}$ et$ y=2+\frac{1}{3}t$ où$ x$ et$ y$ soit mesurée en centimètres. La fonction de température satisfait$ T_x(2,3)=4$ et$ T_y(2,3)=3$. À quelle vitesse la température augmente-t-elle sur la trajectoire de la mouche après une$ 3$ seconde ?

Réponse: $ 2$°C/seconde

44) Les$ y$ composants$ x$ et d'un fluide se déplaçant en deux dimensions sont donnés par les fonctions suivantes :$ u(x,y)=2y$ et$ v(x,y)=−2x$ avec$x≥0$ et$y≥0$. La vitesse du fluide au point$ (x,y)$ est de$ s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}$. Trouvez$ \dfrac{∂s}{∂x}$ et$ \dfrac{∂s}{∂y}$ utilisez la règle de chaîne.

45) Laissez$ u=u(x,y,z),$ où$ x=x(w,t),\, y=y(w,t),\, z=z(w,t),\, w=w(r,s)$ et$ t=t(r,s).$ utilisez un diagramme en arbre et la règle de chaîne pour trouver une expression pour$ \dfrac{∂u}{∂r}$.

Réponse: $ \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})$