14.5 : La règle de chaîne pour les fonctions multivariables
- Page ID
- 197346
- Définissez les règles de chaîne pour une ou deux variables indépendantes.
- Utilisez des diagrammes arborescents pour mieux comprendre la règle de chaîne pour plusieurs variables indépendantes et intermédiaires.
- Effectuez une différenciation implicite d'une fonction de deux variables ou plus.
Dans le calcul à variable unique, nous avons découvert que l'une des règles de différenciation les plus utiles est la règle de chaîne, qui nous permet de trouver la dérivée de la composition de deux fonctions. Il en va de même pour le calcul multivariable, mais cette fois, nous devons traiter de plus d'une forme de règle en chaîne. Dans cette section, nous étudions les extensions de la règle de chaîne et apprenons à prendre des dérivées de compositions de fonctions de plusieurs variables.
Règles de chaîne pour une ou deux variables indépendantes
Rappelons que la règle de chaîne pour la dérivée d'un composite de deux fonctions peut être écrite sous la forme
\[\dfrac{d}{dx}\Big(f(g(x))\Big)=f′\big(g(x)\big)g′(x). \nonumber \]
Dans cette équation, les deux\(f(x)\) et\(g(x)\) sont des fonctions d'une variable. Supposons maintenant que\(f\) c'est une fonction de deux variables et\(g\) qu'elle est fonction d'une variable. Ou peut-être sont-ils tous deux des fonctions de deux variables, voire plus. Comment calculerait-on la dérivée dans ces cas ? Le théorème suivant nous donne la réponse au cas d'une variable indépendante.
Supposons que\(x=g(t)\) et\(y=h(t)\) soient des fonctions dérivables de\(t\) et\(z=f(x,y)\) soient une fonction dérivable de\(x\) et\(y\). \(z=f(x(t),y(t))\)Il s'agit alors d'une fonction dérivable de\(t\) et
\[\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}, \label{chain1} \]
où les dérivées ordinaires sont évaluées à\(t\) et les dérivées partielles sont évaluées à\((x,y)\).
La preuve de ce théorème utilise la définition de la différentiabilité d'une fonction de deux variables. Supposons que cela\(f\) soit dérivable au point\(P(x_0,y_0),\) où\(x_0=g(t_0)\) et\(y_0=h(t_0)\) pour une valeur fixe de\(t_0\). Nous voulons prouver que\(z=f\big(x(t),y(t)\big)\) c'est dérivable à\(t=t_0\) et que l'équation \ ref {chain1} est également valable à ce stade.
Puisque\(f\) c'est différenciable à\(P\), nous savons que
\[z(t)=f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \nonumber \]
où
\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \nonumber \]
On soustrait ensuite\(z_0=f(x_0,y_0)\) des deux côtés de cette équation :
\[ \begin{align*} z(t)−z(t_0) &=f(x(t),y(t))−f(x(t_0),y(t_0)) \\[4pt] &=f_x(x_0,y_0)(x(t)−x(t_0))+f_y(x_0,y_0)(y(t)−y(t_0))+E(x(t),y(t)). \end{align*}\]
Ensuite, nous divisons les deux côtés par\(t−t_0\) :
\[\frac{z(t)−z(t_0)}{t−t_0}=f_x(x_0,y_0)\frac{x(t)−x(t_0)}{t−t_0}+f_y(x_0,y_0)\frac{y(t)−y(t_0)}{t−t_0}+\frac{E(x(t),y(t))}{t−t_0}. \nonumber \]
Ensuite, nous prenons la limite à mesure que l'on\(t\) approche\(t_0\) :
\[\begin{align*} \lim_{t→t_0}\dfrac{z(t)−z(t_0)}{t−t_0} &= f_x(x_0,y_0)\lim_{t→t_0} \left (\dfrac{x(t)−x(t_0)}{t−t_0} \right) \\[4pt] &+f_y(x_0,y_0)\lim_{t→t_0}\left (\dfrac{y(t)−y(t_0)}{t−t_0}\right)\\[4pt] &+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \end{align*}\]
Le côté gauche de cette équation est égal à\(dz/dt\), ce qui conduit à
\[\dfrac{dz}{dt}=f_x(x_0,y_0)\dfrac{dx}{dt}+f_y(x_0,y_0)\dfrac{dy}{dt}+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \nonumber \]
Le dernier terme peut être réécrit comme
\[\begin{align*} \lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0} &=\lim_{t→t_0}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}) \\[4pt] &=\lim_{t→t_0}\left(\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\right)\lim_{t→t_0}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \end{align*} \nonumber \]
À mesure que l'\(t\)\(t_0, \big(x(t),y(t)\big)\)approche\(\big(x(t_0),y(t_0)\big),\), nous pouvons réécrire le dernier produit comme
\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\lim_{(x,y)→(x_0,y_0)}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \nonumber \]
Puisque la première limite est égale à zéro, il suffit de montrer que la seconde limite est finie :
\[ \begin{align*} \lim_{(x,y)→(x_0,y_0)} \dfrac{\sqrt{ (x−x_0)^2+(y−y_0)^2 }} {t−t+0} =\lim_{(x,y)→(x_0,y_0)} \sqrt{ \dfrac { (x−x_0)^2+(y−y_0)^2 } {(t−t_0)^2} } \\[4pt] =\lim_{(x,y)→(x_0,y_0)}\sqrt{ \left(\dfrac{x−x_0}{t−t_0}\right)^2+\left(\dfrac{y−y_0}{t−t_0}\right)^2} \\[4pt] =\sqrt{ \left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{x−x_0}{t−t_0}\right)\right]^2+\left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{y−y_0}{t−t_0}\right)\right]^2}. \end{align*} \nonumber \]
Puisque\(x(t)\) et\(y(t)\) sont tous deux des fonctions dérivables de\(t\), les deux limites à l'intérieur du dernier radical existent. Cette valeur est donc limitée. Cela prouve la règle de la chaîne à\(t=t_0\) ; le reste du théorème repose sur l'hypothèse que toutes les fonctions sont différenciables sur l'ensemble de leurs domaines.
□
Un examen plus approfondi de l'équation \ ref {chain1} révèle un schéma intéressant. Le premier terme de l'équation est\(\dfrac{∂f}{∂x} \cdot \dfrac{dx}{dt}\) et le second terme est\(\dfrac{∂f}{∂y}⋅\dfrac{dy}{dt}\). Rappelez-vous que lors de la multiplication de fractions, l'annulation peut être utilisée. Si nous traitons ces dérivés comme des fractions, chaque produit « se simplifie » en quelque chose de semblable\(∂f/dt\). Les variables\(x\)\(y\) qui disparaissent dans cette simplification sont souvent appelées variables intermédiaires : ce sont des variables indépendantes pour la fonction\(f\), mais des variables dépendantes pour la variable\(t\). Deux termes apparaissent sur le côté droit de la formule et\(f\) sont fonction de deux variables. Ce modèle fonctionne également avec les fonctions de plus de deux variables, comme nous le verrons plus loin dans cette section.
Calculez\(dz/dt\) pour chacune des fonctions suivantes :
- \(z=f(x,y)=4x^2+3y^2,\quad x=x(t)=\sin t,\quad y=y(t)=\cos t\)
- \(z=f(x,y)=\sqrt{x^2−y^2},\quad x=x(t)=e^{2t},\quad y=y(t)=e^{−t}\)
Solution
a. Pour utiliser la règle de la chaîne, nous avons besoin de quatre quantités...\(∂z/∂x,\; ∂z/∂y, \; dx/dt\) et\(dy/dt\) :
- \(\dfrac{∂z}{∂x}=8x\)
- \(\dfrac{dx}{dt}=\cos t\)
- \(\dfrac{∂z}{∂y}=6y\)
- \(\dfrac{dy}{dt}=−\sin t\)
Maintenant, nous les remplaçons dans l'équation \ ref {chain1} :
\ [\ begin {align*} \ dfrac {dz} {dt} &= \ dfrac {\ partial z} {\ partial x} \ cdot \ dfrac {dx} {dt} + \ dfrac {\ partial z} {\ partial y} \ cdot \ dfrac {dy} {dt} \ \ [4pt]
& =( 8x) (\ cos t) (6 ans) (− \ sin t) \ \ [4 points]
&=8x \ cos t−6y \ sin t. \ end {align*} \]
Cette réponse contient trois variables. Pour le réduire à une variable, utilisez le fait que\(x(t)=\sin t\) et\(y(t)=\cos t.\) Nous obtenons
\ [\ begin {align*} \ dfrac {dz} {dt} &=8x \ cos t−6y \ sin t \ \ [4 points]
&=8 (\ sin t) \ cos t−6 (\ cos t) \ sin t \ \ [4 points]
&=2 \ sin t \ cos t. \ end {align*} \]
Cette dérivée peut également être calculée en substituant d'abord\(x(t)\)\(f(x,y),\) puis\(y(t)\) en différenciant ensuite par rapport à\(t\) :
\ [\ begin {align*} z =f (x, y) &=f \ big (x (t), y (t) \ big) \ \ [4 points]
&=4 (x (t)) ^2+3 (y (t)) ^2 \ \ [4 points]
&=4 \ sin^2 t+3 \ cos^2 t. \ end {align*} \]
Alors
\ [\ begin {align*} \ dfrac {dz} {dt} &=2 (4 \ sin t) (\ cos t) +2 (3 \ cos t) (− \ sin t) \ \ [4 points]
&=8 \ sin t \ cos t−6 \ sin t \ cos t \ [4 points]
&=2 \ sin t \ cos t, \ end {align*} \]
ce qui est la même solution. Cependant, il n'est pas toujours aussi facile de faire la différence sous cette forme.
b. Pour utiliser la règle de la chaîne, nous avons encore une fois besoin de quatre quantités...\(∂z/∂x,∂z/dy,dx/dt,\) et\(dy/dt:\)
- \(\dfrac{∂z}{∂x}=\dfrac{x}{\sqrt{x^2−y^2}}\)
- \(\dfrac{dx}{dt}=2e^{2t}\)
- \(\dfrac{∂z}{∂y}=\dfrac{−y}{\sqrt{x^2−y^2}}\)
- \(\dfrac{dx}{dt}=−e^{−t}.\)
Nous les remplaçons dans l'équation \ ref {chain1} :
\ [\ begin {align*} \ dfrac {dz} {dt} &= \ dfrac {\ partial z} {\ partial x} \ cdot \ dfrac {dx} {dt} + \ dfrac {\ partial z} {\ partial y} \ cdot \ dfrac {dy} {dt} \ \ [4pt] &= \ left (\ dfrac {x} {\ sqrt {x^2−y^2}} \ droite) (2e^ {2t}) + \ gauche (\ dfrac {−y} {\ sqrt {x^2−y^2}} \ droite) (−e^ {−t}) \ \ [4 points]
&= \ dfrac {2xe^ {2t} −ye^ {−t}} {\ sqrt {x^2−y^2}}. \ end {align*} \ nonumber \]
Pour réduire cela à une variable, nous utilisons le fait que\(x(t)=e^{2t}\) et\(y(t)=e^{−t}\). Par conséquent,
\ [\ begin {align*} \ dfrac {dz} {dt} &= \ dfrac {2xe^2t+ye^ {−t}} {\ sqrt {x^2−y^2}} \ \ [4pt]
&= \ dfrac {2 (e^ {2t}) e^ {2t} + (e^ {−t}) e^ {−t}) e^ {−t}) e^ {−t}}} {\ sqrt {e^ {4t} −e^ {−2t}}} \ \ [4 points]
&= \ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}}}. \ end {align*} \ nonumber \]
Pour éliminer les exposants négatifs, on multiplie le haut par\(e^{2t}\) et le bas par\(\sqrt{e^{4t}}\) :
\ [\ begin {align*} \ dfrac {dz} {dt} &= \ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}} ⋅ \ dfrac {e^ {2t}} {\ sqrt {e^ {4t}}} \ \ [4pt]
&= \ dfrac {2e^ {6t} +1} {\ sqrt {e^ {8t} −e^ {2t}}} \ \ [4 points]
&= \ dfrac {2e^ {6t} +1} {\ sqrt {e^ {2t} (e^ {6t} −1)}} \ \ [4 points] &= \ dfrac {2 t} (e^ {6t} −1)}} \ \ [4 points]
&= \ dfrac {2 t} e^ {6t} +1} {e^t \ sqrt {e^ {6 t} −1}}. \ end {align*} \]
Encore une fois, cette dérivée peut également être calculée en substituant d'abord\(x(t)\)\(f(x,y),\) puis\(y(t)\) en différenciant ensuite par rapport à\(t\) :
\[\begin{align*} z &=f(x,y) \\[4pt] &=f(x(t),y(t)) \\[4pt] &=\sqrt{(x(t))^2−(y(t))^2} \\[4pt] &=\sqrt{e^{4t}−e^{−2t}} \\[4pt] &=(e^{4t}−e^{−2t})^{1/2}. \end{align*} \nonumber \]
Alors
\[ \begin{align*} \dfrac{dz}{dt} &= \dfrac{1}{2} (e^{4t}−e^{−2t})^{−1/2} \left(4e^{4t}+2e^{−2t} \right) \\[4pt] &=\dfrac{2e^{4t}+e^{−2t}}{\sqrt{e^{4t}−e^{−2t}}}. \end{align*}\]
Il s'agit de la même solution.
\(dz/dt \)Calculez à l'aide des fonctions suivantes. Exprimez la réponse finale en termes de\(t\).
\[ \begin{align*} z =f(x,y) &=x^2−3xy+2y^2,\\[4pt] x =x(t) &=3\sin 2t,\\[4pt] y=y(t) &=4\cos 2t \end{align*}\]
- Allusion
-
Calculez\(∂z/∂x,∂z/dy,dx/dt,\) puis\(dy/dt\) utilisez l'équation \ ref {chain1}.
- Réponse
-
\ (\ begin {align*} \ dfrac {dz} {dt} &= \ dfrac {δf} {δx} \ dfrac {dx} {dt} + \ dfrac {stadt} {dy} {dt} \ \ [5 points]
& =( 2x−3 ans) (6 \ cos 2t) + (−3x+4 points) y) (−8 \ sin 2t) \ \ [5 points]
&=−92 \ sin 2t \ cos 2t−72 (\ cos ^22t− \ sin^2 2 points) \ \ [5 points]
&=−46 \ sin 4t−72 \ cos 4 t. \ end {align*} \)
Il est souvent utile de créer une représentation visuelle de l'équation \ ref {chain1} pour la règle de chaîne. C'est ce que l'on appelle un diagramme en arbre pour la règle de chaîne pour les fonctions d'une variable et il permet de mémoriser la formule (Figure\(\PageIndex{1}\)). Ce diagramme peut être étendu aux fonctions de plusieurs variables, comme nous le verrons très prochainement.
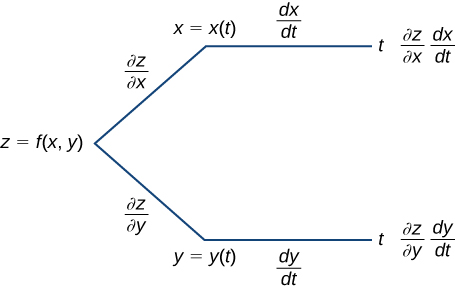
Dans ce schéma, le coin le plus à gauche correspond à\(z=f(x,y)\). Comme il\(f\) possède deux variables indépendantes, deux lignes partent de ce coin. La branche supérieure correspond à la variable\(x\) et la branche inférieure correspond à la variable\(y\). Comme chacune de ces variables dépend alors d'une variable\(t\), une branche provient alors\(x\) et une branche vient de\(y\). Enfin, chacune des branches situées à l'extrême droite possède une étiquette qui représente le chemin parcouru pour atteindre cette branche. La branche supérieure est atteinte en suivant la\(x\) branche, puis la branche t ; elle est donc étiquetée\((∂z/∂x)×(dx/dt).\) La branche inférieure est similaire : d'abord la\(y\) branche, puis la\(t\) branche. Cette branche est étiquetée\((∂z/∂y)×(dy/dt)\). Pour obtenir la formule permettant d'\(dz/dt,\)ajouter tous les termes qui apparaissent à l'extrême droite du diagramme. Cela nous donne l'équation.
Dans Note,\(z=f(x,y)\) est fonction de\(x\) et\(y\), et les deux\(x=g(u,v)\) et\(y=h(u,v)\) sont des fonctions des variables indépendantes\(u\) et\(v\).
Supposons\(x=g(u,v)\) et\(y=h(u,v)\) sont des fonctions dérivables de\(u\) et\(v\), et\(z=f(x,y)\) est une fonction dérivable de\(x\) et\(y\). Alors,\(z=f(g(u,v),h(u,v))\) est une fonction dérivable de\(u\) et\(v\), et
\[\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂u} \label{chain2a} \]
et
\[\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v}. \label{chain2b} \]
Nous pouvons dessiner un diagramme arborescent pour chacune de ces formules ainsi que les suivantes.
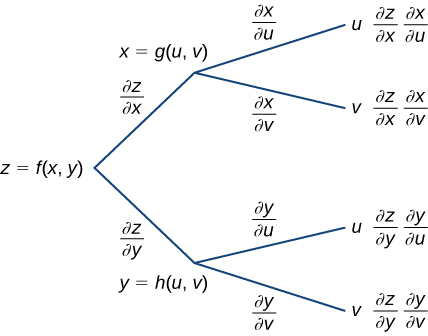
Pour obtenir la formule de\(∂z/∂u\), commencez par le côté gauche du diagramme, puis suivez uniquement les branches qui se terminent par\(u\) et ajoutez les termes qui apparaissent à la fin de ces branches. Pour la formule\(∂z/∂v\), suivez uniquement les branches qui se terminent par\(v\) et ajoutez les termes qui apparaissent à la fin de ces branches.
Il existe une différence importante entre ces deux théorèmes de règles en chaîne. Dans la note, le côté gauche de la formule de la dérivée n'est pas une dérivée partielle, mais dans la note, elle l'est. La raison en est que, dans Note,\(z\) est finalement fonction de\(t\) seul, alors que dans Note,\(z\) est fonction à la fois de\(u\) et\(v\).
Calculez\(∂z/∂u\) et\(∂z/∂v\) utilisez les fonctions suivantes :
\[z=f(x,y)=3x^2−2xy+y^2,\; x=x(u,v)=3u+2v,\; y=y(u,v)=4u−v. \nonumber \]
Solution
Pour implémenter la règle de chaîne pour deux variables, nous avons besoin de six dérivées partielles\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\) et\(∂y/∂v\) :
\[\begin{align*} \dfrac{∂z}{∂x} &=6x−2y & & \dfrac{∂z}{∂y}=−2x+2y \\[4pt] \dfrac{∂x}{∂u} &=3 & & \dfrac{∂x}{∂v}=2 \\[4pt] \dfrac{∂y}{∂u} &=4 & & \dfrac{∂y}{∂v}=−1. \end{align*}\]
Pour le trouver,\(∂z/∂u,\) nous utilisons l'équation \ ref {chain2a} :
\ [\ begin {align*} \ dfrac {δz} {δu} &= \ dfrac {δz} {δx} ⋅ \ dfrac {δx} {sut} + \ dfrac {⌘z} {66.y} ⋅ \ dfrac {66.y} {⌘u} \ \ [4 points]
&=3 (6x−2 ans) +4 (−2x+y) +4 (−2x+y) 2 ans) \ \ [4 points]
&=10 x+2 ans. \ end {align*} \]
Ensuite, nous remplaçons\(x(u,v)=3u+2v\) et\(y(u,v)=4u−v:\)
\[\begin{align*} \dfrac{∂z}{∂u} &=10x+2y \\[4pt] &=10(3u+2v)+2(4u−v) \\[4pt] &=38u+18v. \end{align*}\]
Pour le trouver,\(∂z/∂v,\) nous utilisons l'équation \ ref {chain2b} :
\[\begin{align*} \dfrac{∂z}{∂v} &=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v} \\[4pt] &=2(6x−2y)+(−1)(−2x+2y) \\[4pt] &=14x−6y. \end{align*}\]
Ensuite, nous remplaçons\(x(u,v)=3u+2v\) et\(y(u,v)=4u−v:\)
\[\begin{align*} \dfrac{∂z}{∂v} &=14x−6y \\[4pt] &=14(3u+2v)−6(4u−v) \\[4pt] &=18u+34v \end{align*}\]
Calculez\(∂z/∂u\)\(∂z/∂v\) et utilisez les fonctions suivantes :
\[ z=f(x,y)=\dfrac{2x−y}{x+3y},\quad x(u,v)=e^{2u}\cos 3v,\quad y(u,v)=e^{2u}\sin 3v. \nonumber \]
- Allusion
-
Calculez\(∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,\) puis\(∂y/∂v\) utilisez l'équation \ ref {chain2a} et l'équation \ ref {chain2b}.
- Réponse
-
\(\dfrac{∂z}{∂u}=0,\quad \dfrac{∂z}{∂v}=\dfrac{−21}{(3\sin 3v+\cos 3v)^2}\)
La règle de la chaîne généralisée
Maintenant que nous avons vu comment étendre la règle de chaîne d'origine aux fonctions de deux variables, il est naturel de se demander : pouvons-nous étendre la règle à plus de deux variables ? La réponse est oui, comme l'indique la règle de la chaîne généralisée.
\(w=f(x_1,x_2,…,x_m)\)Soit une fonction dérivable de variables\(m\) indépendantes, et pour chacune\(i∈{1,…,m},\)\(x_i=x_i(t_1,t_2,…,t_n)\) soit une fonction dérivable de variables\(n\) indépendantes. Alors
\[\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_2}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j} \nonumber \]
pour tous\(j∈{1,2,…,n}.\)
Dans l'exemple suivant, nous calculons la dérivée d'une fonction de trois variables indépendantes dans laquelle chacune des trois variables dépend de deux autres variables.
Calculez\(∂w/∂u\) et\(∂w/∂v\) utilisez les fonctions suivantes :
\[\begin{align*} w &=f(x,y,z)=3x^2−2xy+4z^2 \\[4pt] x &=x(u,v)=e^u\sin v \\[4pt] y &=y(u,v)=e^u\cos v \\[4pt] z &=z(u,v)=e^u. \end{align*}\]
Solution
Les formules pour\(∂w/∂u\) et\(∂w/∂v\) sont
\[\begin{align*} \dfrac{∂w}{∂u} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v}. \end{align*}\]
Par conséquent, neuf dérivées partielles différentes doivent être calculées et substituées. Nous devons calculer chacun d'eux :
\[\begin{align*} \dfrac{∂w}{∂x}&=6x−2y \dfrac{∂w}{∂y}=−2x \dfrac{∂w}{∂z}=8z \\[4pt] \dfrac{∂x}{∂u}&=e^u\sin v \dfrac{∂y}{∂u}=e^u\cos v \dfrac{∂z}{∂u}=e^u \\[4pt] \dfrac{∂x}{∂v}&=e^u\cos v \dfrac{∂y}{∂v}=−e^u\sin v \dfrac{∂z}{∂v}=0. \end{align*}\]
Maintenant, nous les substituons dans la première formule pour calculer\( ∂w/∂u\) :
\ [\ begin {align*} \ dfrac {δw} {δu} &= \ dfrac {δw} {δx} ⋅ \ dfrac {δx} {⌘u} + \ dfrac {{△ u} \ \ [4 points]
& =( 6x−2y) e^u \ sin v−2xe^u \ cos v+8ze^u, \ end {align*} \]
puis remplacez\(x(u,v)=e^u \sin v, \, y(u,v)=e^u\cos v,\) et\(z(u,v)=e^u\) dans cette équation :
\[\begin{align*} \dfrac{∂w}{∂u} &=(6x−2y)e^u\sin v−2xe^u\cos v+8ze^u \\[4pt] &=(6e^u\sin v−2eu\cos v)e^u\sin v−2(e^u\sin v)e^u\cos v+8e^{2u} \\[4pt] &=6e^{2u}\sin^2 v−4e^{2u}\sin v\cos v+8e^{2u} \\[4pt] &=2e^{2u}(3\sin^2 v−2\sin v\cos v+4). \end{align*}\]
Ensuite, nous calculons\(∂w/∂v\) :
\[\begin{align*} \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v} \\[4pt] &=(6x−2y)e^u\cos v−2x(−e^u\sin v)+8z(0), \end{align*}\]
alors on remplace\(x(u,v)=e^u\sin v,\, y(u,v)=e^u\cos v,\) et\(z(u,v)=e^u\) dans cette équation :
\[\begin{align*} \dfrac{∂w}{∂v} &=(6x−2y)e^u\cos v−2x(−e^u\sin v) \\[4pt] &=(6e^u \sin v−2e^u\cos v)e^u\cos v+2(e^u\sin v)(e^u\sin v) \\[4pt] &=2e^{2u}\sin^2 v+6e^{2u}\sin v\cos v−2e^{2u}\cos^2 v \\[4pt] &=2e^{2u}(\sin^2 v+\sin v\cos v−\cos^2 v). \end{align*}\]
Calculez\(∂w/∂u\)\(∂w/∂v\) et utilisez les fonctions suivantes :
\[\begin{align*} w &=f(x,y,z)=\dfrac{x+2y−4z}{2x−y+3z} \\[4pt] x &=x(u,v)=e^{2u}\cos3v \\[4pt] y &=y(u,v)=e^{2u}\sin 3v \\[4pt] z &=z(u,v)=e^{2u}. \end{align*}\]
- Allusion
-
Calculez neuf dérivées partielles, puis utilisez les mêmes formules que celles de l'exemple\(\PageIndex{3}\).
- Réponse
-
\(\dfrac{∂w}{∂u}=0\)
\(\dfrac{∂w}{∂v}=\dfrac{15−33\sin 3v+6\cos 3v}{(3+2\cos 3v−\sin 3v)^2}\)
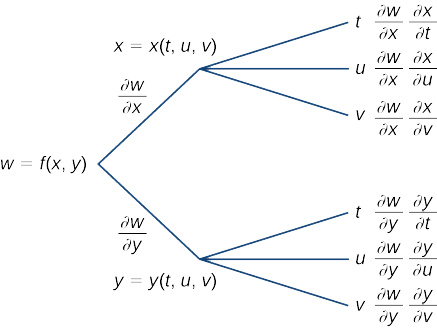
Créez un diagramme arborescent pour le cas où
\[ w=f(x,y,z),\quad x=x(t,u,v),\quad y=y(t,u,v),\quad z=z(t,u,v) \nonumber \]
et écrivez les formules pour les trois dérivées partielles de\(w\).
Solution
En partant de la gauche, la fonction\(f\) comporte trois variables indépendantes :\(x,\, y\), et\(z\). Par conséquent, trois branches doivent émaner du premier nœud. Chacune de ces trois branches possède également trois branches, pour chacune des variables\(t,\, u,\) et\(v\).

Les trois formules sont
\[\begin{align*} \dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂v}. \end{align*}\]
Créez un diagramme arborescent pour le cas où
\[w=f(x,y),\quad x=x(t,u,v),\quad y=y(t,u,v) \nonumber \]
et écrivez les formules pour les trois dérivées partielles de\(w.\)
- Allusion
-
Déterminez le nombre de branches qui émanent de chaque nœud de l'arbre.
- Réponse
-
\[\begin{align*}\dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v} \end{align*}\]
Différenciation implicite
Le rappel de la différenciation implicite fournit une méthode pour\(dy/dx\) déterminer quand\(y\) est défini implicitement en fonction de\(x\). La méthode consiste à différencier les deux côtés de l'équation définissant la fonction par rapport à\(x\), puis à résoudre les dérivées\(dy/dx.\) partielles pour fournir une alternative à cette méthode.
Considérez l'ellipse définie par l'équation\(x^2+3y^2+4y−4=0\) comme suit.
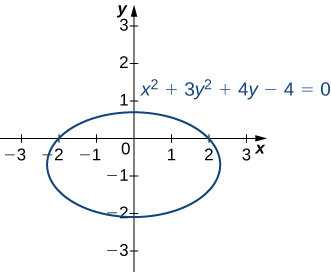
Cette équation se définit implicitement\(y\) comme une fonction de\(x\). Ainsi, nous pouvons trouver la dérivée\(dy/dx\) en utilisant la méthode de différenciation implicite :
\[\begin{align*} \dfrac{d}{dx}(x^2+3y^2+4y−4) &=\dfrac{d}{dx}(0) \\[4pt] 2x+6y\dfrac{dy}{dx}+4\dfrac{dy}{dx} &=0 \\[4pt] (6y+4)\dfrac{dy}{dx} &=−2x\\[4pt] \dfrac{dy}{dx} &=−\dfrac{x}{3y+2}\end{align*}\]
Nous pouvons également définir une fonction en\(z=f(x,y)\) utilisant le côté gauche de l'équation définissant l'ellipse. Ensuite,\(f(x,y)=x^2+3y^2+4y−4.\) l'ellipse\(x^2+3y^2+4y−4=0\) peut être décrite par l'équation\(f(x,y)=0\). L'utilisation de cette fonction et du théorème suivant nous donne une approche alternative pour le calcul\(dy/dx.\)
Supposons que la fonction se\(z=f(x,y)\) définisse\(y\) implicitement comme une fonction\(y=g(x)\) de\(x\) via l'équation\(f(x,y)=0.\) Alors
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y} \label{implicitdiff1} \]
fourni\(f_y(x,y)≠0.\)
Si l'équation se\(f(x,y,z)=0\) définit\(z\) implicitement comme une fonction dérivable de\(x\) et\(y\), alors
\[\dfrac{dz}{dx}=−\dfrac{∂f/∂x}{∂f/∂z} \qquad\text{and}\qquad \dfrac{dz}{dy}=−\dfrac{∂f/∂y}{∂f/∂z}\label{implicitdiff2} \]
tant que\(f_z(x,y,z)≠0.\)
L'équation \ ref {implicitdiff1} est une conséquence directe de l'équation \ ref {chain2a}. En particulier, si nous supposons que cela\(y\) est défini implicitement en fonction de\(x\) via l'équation\(f(x,y)=0\), nous pouvons appliquer la règle de la chaîne pour trouver\(dy/dx:\)
\[\begin{align*} \dfrac{d}{dx}f(x,y) &=\dfrac{d}{dx}(0) \\[4pt] \dfrac{∂f}{∂x}⋅\dfrac{dx}{dx}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0 \\[4pt]\dfrac{∂f}{∂x}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0. \end{align*}\]
La résolution de cette équation pour\(dy/dx\) donne l'équation \ ref {implicitdiff1}. L'équation \ ref {implicitdiff1} peut être dérivée de la même manière.
Revenons maintenant au problème que nous avons commencé avant le théorème précédent. En utilisant Note et la fonction\(f(x,y)=x^2+3y^2+4y−4,\) que nous obtenons
\[\begin{align*} \dfrac{∂f}{∂x} &=2x\\[4pt] \dfrac{∂f}{∂y} &=6y+4. \end{align*}\]
Ensuite, l'équation \ ref {implicitdiff1} donne
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=−\dfrac{2x}{6y+4}=−\dfrac{x}{3y+2}, \nonumber \]
ce qui est le même résultat obtenu par l'utilisation antérieure de la différenciation implicite.
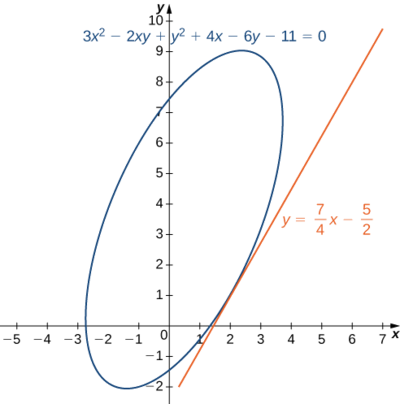
- Calculez\(dy/dx\) si elle\(y\) est définie implicitement en fonction de\(x\) via l'équation\(3x^2−2xy+y^2+4x−6y−11=0\). Quelle est l'équation de la tangente au graphe de cette courbe en un point\((2,1)\) ?
- Calculer\(∂z/∂x\) et\(∂z/∂y,\) donner\(x^2e^y−yze^x=0.\)
Solution
a. Réglez\(f(x,y)=3x^2−2xy+y^2+4x−6y−11=0,\) puis calculez\(f_x\)\(f_y: f_x(x,y)=6x−2y+4\) et\(f_y(x,y)=−2x+2y−6.\)
La dérivée est donnée par
\[\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=\dfrac{6x−2y+4}{−2x+2y−6}=\dfrac{3x−y+2}{x−y+3}. \nonumber \]
La pente de la tangente au point\((2,1)\) est donnée par
\[\dfrac{dy}{dx}\Bigg|_{(x,y)=(2,1)}=\dfrac{3(2)−1+2}{2−1+3}=\dfrac{7}{4} \nonumber \]
Pour trouver l'équation de la tangente, nous utilisons la forme de pente ponctuelle (Figure\(\PageIndex{5}\)) :
\[\begin{align*} y−y_0 &=m(x−x_0)\\[4pt]y−1 &=\dfrac{7}{4}(x−2) \\[4pt] y &=\dfrac{7}{4}x−\dfrac{7}{2}+1\\[4pt] y &=\dfrac{7}{4}x−\dfrac{5}{2}.\end{align*}\]
b. Nous avons\(f(x,y,z)=x^2e^y−yze^x.\) donc,
\[\begin{align*} \dfrac{∂f}{∂x} &=2xe^y−yze^x \\[4pt] \dfrac{∂f}{∂y} &=x^2e^y−ze^x \\[4pt] \dfrac{∂f}{∂z} &=−ye^x\end{align*}\]
En utilisant l'équation \ ref {implicitdiff2},
\[\begin{align*} \dfrac{∂z}{∂x} &=−\dfrac{∂f/∂x}{∂f/∂y} & &\text{and} & \dfrac{∂z}{∂y} =−\dfrac{∂f/∂y}{∂f/∂z} \\[4pt] &=−\dfrac{2xe^y−yze^x}{−ye^x} & & &=−\dfrac{x^2e^y−ze^x}{−ye^x} \\[4pt] &=\dfrac{2xe^y−yze^x}{ye^x} & & & =\dfrac{x^2e^y−ze^x}{ye^x} \end{align*}\]
\(dy/dx\)Détermine si elle\(y\) est définie implicitement\(x\) en fonction de l'équation\(x^2+xy−y^2+7x−3y−26=0\). Quelle est l'équation de la tangente au graphe de cette courbe en un point\((3,−2)\) ?
- Allusion
-
Calculez\(∂f/dx\) puis\(∂f/dy\) utilisez l'équation \ ref {implicitdiff1}.
- Solution
-
\[\dfrac { d y } { d x } = \left. \frac { 2 x + y + 7 } { 2 y - x + 3 } \right| _ { ( 3 , - 2 ) } = \dfrac { 2 ( 3 ) + ( - 2 ) + 7 } { 2 ( - 2 ) - ( 3 ) + 3 } = - \dfrac { 11 } { 4 } \nonumber \]
Équation de la tangente :\(y=−\dfrac{11}{4}x+\dfrac{25}{4}\)
Concepts clés
- La règle de chaîne pour les fonctions de plus d'une variable implique les dérivées partielles par rapport à toutes les variables indépendantes.
- Les diagrammes arborescents sont utiles pour dériver des formules pour la règle de chaîne pour les fonctions de plusieurs variables, chaque variable indépendante dépendant également d'autres variables.
Équations clés
- Règle de chaîne, une variable indépendante
\(\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}\)
- Règle de chaîne, deux variables indépendantes
\(\dfrac{dz}{du}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}\dfrac{dz}{dv}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}\)
- Règle de chaîne généralisée
\(\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_1}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j}\)
Lexique
- règle de chaîne généralisée
- la règle de chaîne étendue aux fonctions de plusieurs variables indépendantes, dans laquelle chaque variable indépendante peut dépendre d'une ou de plusieurs autres variables
- variable intermédiaire
- étant donné une composition de fonctions (par exemple\(f(x(t),y(t)))\), les variables intermédiaires sont les variables qui sont indépendantes dans la fonction externe mais qui dépendent également d'autres variables ; dans la fonction,\(f(x(t),y(t)),\) les variables\(x\) et\(y\) sont des exemples de variables intermédiaires
- diagramme d'arbre
- illustre et dérive des formules pour la règle de la chaîne généralisée, dans laquelle chaque variable indépendante est prise en compte


