Skip to main content
Global

14.4E : Exercices pour la section 14.4

  1. Last updated
  2. Save as PDF
  • Page ID
    197335

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 2, trouvez un vecteur normal unitaire par rapport à la surface au point indiqué.

    1)\( f(x,y)=x^3,\quad (2,−1,8)\)

    Réponse
    \( (\frac{\sqrt{145}}{145})(12\hat{\mathbf i}−\hat{\mathbf k})\)

    2)\( \ln\left(\dfrac{x}{y−z}\right)=0\) quand\( x=y=1\)

    Dans les exercices 3 à 7, trouvez un vecteur normal et un vecteur tangent au point\( P\).

    3)\( x^2+xy+y^2=3,\quad P(−1,−1)\)

    Réponse
    Vecteur normal :\( \hat{\mathbf i}+\hat{\mathbf j}\), vecteur tangent :\( \hat{\mathbf i}−\hat{\mathbf j}\)

    4)\( (x^2+y^2)^2=9(x^2−y^2),\quad P(\sqrt{2},1)\)

    5)\( xy^2−2x^2+y+5x=6,\quad P(4,2)\)

    Réponse
    Vecteur normal :\( 7\hat{\mathbf i}−17\hat{\mathbf j}\), vecteur tangent :\( 17\hat{\mathbf i}+7\hat{\mathbf j}\)

    6)\( 2x^3−x^2y^2=3x−y−7,\quad P(1,−2)\)

    7)\( ze^{x^2−y^2}−3=0, \quad P(2,2,3)\)

    Réponse
    Vecteur normal :\( -12\hat{\mathbf i}+12\hat{\mathbf j}-\hat{\mathbf k}\) ou\( 12\hat{\mathbf i}-12\hat{\mathbf j}+\hat{\mathbf k}\) Vecteur
    tangent :\( 0\hat{\mathbf i}+1\hat{\mathbf j}+12\hat{\mathbf k}\) ou\( 1\hat{\mathbf i}+0\hat{\mathbf j}-12\hat{\mathbf k}\)

    Dans les exercices 8 à 19, trouvez l'équation du plan tangent à la surface au point indiqué. (Conseil : si la fonction donnée n'est pas déjà résolue\(z\), commencez par la résoudre\( z\) en termes de\( x\) et\( y\).)

    8)\( −8x−3y−7z=−19,\quad P(1,−1,2)\)

    9)\( z=−9x^2−3y^2,\quad P(2,1,−39)\)

    Réponse
    \( −36x−6y−z=−39\)

    10)\( x^2+10xyz+y^2+8z^2=0,\quad P(−1,−1,−1)\)

    11)\( z=\ln(10x^2+2y^2+1),\quad P(0,0,0)\)

    Réponse
    \( z=0\)

    (12)\( z=e^{7x^2+4y^2}, \quad P(0,0,1)\)

    13)\( xy+yz+zx=11,\quad P(1,2,3)\)

    Réponse
    \( 5x+4y+3z−22=0\)

    (14)\( x^2+4y^2=z^2,\quad P(3,2,5)\)

    15)\( x^3+y^3=3xyz,\quad P(1,2,\frac{3}{2})\)

    Réponse
    \( 4x−5y+4z=0\)

    16)\( z=axy,\quad P(1,\frac{1}{a},1)\)

    17)\( z=\sin x+\sin y+\sin(x+y),\quad P(0,0,0)\)

    Réponse
    \( 2x+2y−z=0\)

    18)\( h(x,y)=\ln\sqrt{x^2+y^2},\quad P(3,4)\)

    19)\( z=x^2−2xy+y^2,\quad P(1,2,1)\)

    Réponse
    \( −2(x−1)+2(y−2)−(z−1)=0\)

    Dans les exercices 20 à 25, trouvez des équations paramétriques pour la ligne normale menant à la surface au point indiqué. (N'oubliez pas que pour trouver l'équation d'une droite dans l'espace, vous avez besoin d'un point sur la droite et d'un vecteur\( \vecs v=⟨a,b,c⟩\) parallèle à la droite.\( P_0(x_0,y_0,z_0)\) Les équations de la droite sont alors les suivantes :\(\quad x=x_0+at,\quad y=y_0+bt, \quad z=z_0+ct.)\)

    20)\( −3x+9y+4z=−4,\quad P(1,−1,2)\)

    (21)\( z=5x^2−2y^2,\quad P(2,1,18)\)

    Réponse
    \( x=20t+2,y=−4t+1,z=−t+18\)

    22)\( x^2−8xyz+y^2+6z^2=0,\quad P(1,1,1)\)

    23)\( z=\ln(3x^2+7y^2+1),\quad P(0,0,0)\)

    Réponse
    \( x=0,y=0,z=t\)

    (24)\( z=e^{4x^2+6y^2},\quad P(0,0,1)\)

    25)\( z=x^2−2xy+y^2\) au point\( P(1,2,1)\)

    Réponse
    \( x−1=2t;y−2=−2t;z−1=t\)

    Dans les exercices 26 à 28, utilisez la figure présentée ici.

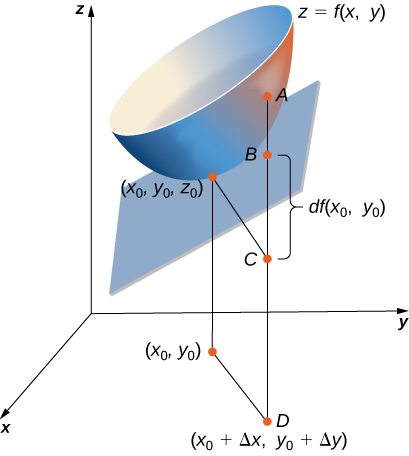
    Schéma montrant le différentiel de f au point (x_0, y_0)

    26) La longueur du segment de ligne\( AC\) est égale à quelle expression mathématique ?

    27) La longueur du segment de ligne\( BC\) est égale à quelle expression mathématique ?

    Réponse
    Le différentiel de la fonction\( z(x,y)=dz=f_xdx+f_ydy\)

    28) À l'aide de la figure, expliquez ce que\( AB\) représente la longueur du segment de ligne.

    29) Montrez que\( f(x,y)=e^{xy}x\) c'est différenciable au point\( (1,0).\)

    Réponse
    En utilisant la définition de la différentiabilité, nous avons\( e^{xy}x≈x+y\).

    30) Montrez que\( f(x,y)=x^2+3y\) c'est différenciable à chaque point. En d'autres termes, montrez que\( Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy\), où les deux\( ε_1\) et\( ε_2\) approchent de zéro à mesure que\( (Δx,Δy)\)\( (0,0).\)

    Réponse
    \( Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0\)pour les petits\( Δx\) et\( z\) répond à la définition de la différentiabilité.

    31) Déterminez le différentiel total de chaque fonction :

    1. \( z=x^3 + y^3 - 5\)
    2. \( z=e^{xy}\)
    3. \( z=y\cos x+\sin y\)
    4. \(P = t^2 + 3t + tu^3\)
    5. \( w=e^y\cos(x)+z^2\)
    Réponses :
    1. \( dz = 3x^2\,dx +3y^2\,dy \)
    2. \( dz = ye^{xy}\,dx +xe^{xy}\,dy \)
    3. \( dz = -y\sin x\,dx +(\cos x + \cos y)\,dy \)
    4. \( dP = (2t + 3 + u^3)\, dt + 3t u^2 \,du \)
    5. \( dw = -e^y\sin(x)\,dx +e^y\cos(x)\,dy +2z\,dz\)

    32) a. Trouvez le différentiel total\(dz\) de la fonction,\( z=\dfrac{xy}{y+x}\) puis
    b. Indiquez sa valeur où\( x\) change de\( 10\) à\( 10.5\) et\( y\) change de\( 15\) à\( 13\).

    Réponse
    a.\( dz = \dfrac{y^2}{(x+y)^2}\, dx + \dfrac{x^2}{(x+y)^2} \,dy \)
    b.\(dx = 0.5\) et\(dy = -2\) donc

     \ (\ begin {align*} dz &= f_x (10, 15) \, dx + f_y (10,15) \, dy \ \
    &= \ frac {15^2}} {25^2} \, dx + \ frac {10^2} {25^2} \, dy \ \
    &= \ frac {225} {625} \, (0,5) + \ frac {100} { 625} (-2) \ \
    &= \ frac {9} {25} \ gauche (\ frac {1} {2} \ droite) + \ frac {4} {25} (-2) \ \
    &= \ frac {18} {100} - \ frac {32} {100} \ \
    &= 0,18 - 0,32 = -0,14 \ end {align*} \)

    33)\( z=f(x,y)=xe^y.\) Exprimons son différentiel total. Calculez ensuite\( Δz\) de\( P(1,2)\) à,\( Q(1.05,2.1)\) puis trouvez la variation approximative de\( z\)\(dz\), d'un point\( P\) à l'autre\( Q\). Rappelez-vous\( Δz=f(x+Δx,y+Δy)−f(x,y)\), et\( dz\) et\( Δz\) devraient être à peu près égaux, si\(dx\) les deux\(dy\) sont raisonnablement petits.

    Réponse
    Différentiel total :\(dz = e^y\,dx + xe^y\, dy \)
    \( Δz≈1.185422\) et\( dz≈1.108.\) notez qu'ils sont relativement proches.

    34) Le volume d'un cylindre circulaire droit est donné par\( V(r,h)=πr^2h.\) Find the differential\( dV\). Interprétez la formule de manière géométrique.

    Réponse
    \( dV = 2 \pi r h\, dr + \pi r^2 \,dh \)

    35) Voir le problème précédent. Utilisez des différentiels pour estimer la quantité d'aluminium dans une boîte en aluminium fermée avec un diamètre\( 8.0cm\) et une hauteur\( 12cm\) si l'aluminium a une épaisseur de\( 0.04\) cm.

    Réponse
    \( 16\,\text{cm}^3\)

    36) Utilisez le différentiel\( dz\) pour approximer la variation lorsque vous\( z=\sqrt{4−x^2−y^2}\) vous\( (x,y)\) déplacez d'un point\( (1,1)\) à l'autre.\( (1.01,0.97).\) Comparez cette approximation avec la modification réelle de la fonction.

    37)\( z=f(x,y)=x^2+3xy−y^2.\) Trouvons le changement exact de la fonction et le changement approximatif de la fonction sous forme de\( x\) changements de\( 2.00\) à\( 2.05\) et de\( y\) changements de\( 3.00\) à\( 2.96\).

    Réponse
    \( Δz=\)changement exact\( =0.6449\), changement approximatif est\( dz=0.65\). Les deux valeurs sont proches.

    38) L'accélération centripète d'une particule se déplaçant dans un cercle est donnée par\( a(r,v)=\frac{v^2}{r},\) où\( v\) sont la vitesse et\( r\) le rayon du cercle. Approximation de l'erreur maximale en pourcentage lors de la mesure de l'accélération résultant d'erreurs\( 3\%\) d'entrée\( v\) et\( 2\%\) d'entrée\( r\). (Rappelez-vous que le pourcentage d'erreur est le ratio entre le montant de l'erreur et le montant initial. Donc, dans ce cas, le pourcentage d'erreur dans a est donné par\( \frac{da}{a}\).)

    39) Le rayon\( r\) et la hauteur\( h\) d'un cylindre circulaire droit sont mesurés avec des erreurs possibles de\( 4\%\) et\( 5\%\), respectivement. Approximation du pourcentage d'erreur maximal possible lors de la mesure du volume (Rappelez-vous que le pourcentage d'erreur est le rapport entre le degré d'erreur et le montant initial). Donc, dans ce cas, le pourcentage d'erreur dans\( V\) est donné par\( \frac{dV}{V}\).)

    Réponse
    \( 13\%\)ou\( 0.13\)

    40) Le rayon de base et la hauteur d'un cône circulaire droit sont mesurés\( 25\) en\( 10\) pouces et en pouces, respectivement, avec une erreur de mesure possible d'autant que\( 0.1\) dans chacun. Utilisez des différentiels pour estimer l'erreur maximale dans le volume calculé du cône.

    41) La résistance électrique\( R\) produite par les résistances de câblage\( R_1\) et\( R_2\) en parallèle peut être calculée à partir de la formule\( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\). Si\( R_1\) et\( R_2\) sont mesurés comme étant\( 7Ω\) et\( 6Ω\), respectivement, et si ces mesures sont précises\( 0.05Ω\), estimez l'erreur informatique maximale possible\( R\). (Le symbole\( Ω\) représente un ohm, l'unité de résistance électrique.)

    Réponse
    \( 0.025\)

    42) L'aire d'une ellipse avec des axes de longueur\( 2a\) et\( 2b\) est donnée par la formule\( A=πab\). Approximation de la variation en pourcentage de la surface lorsque\( a\) celle-ci augmente de\( 2\%\) et\( b\) augmente de\( 1.5\%.\)

    43) La période\( T\) d'un pendule simple à petites oscillations est calculée à partir de la formule\( T=2π\sqrt{\frac{L}{g}}\), où\( L\) est la longueur du pendule et\( g\) l'accélération résultant de la gravité. Supposons cela\( L\) et\( g\) ayez des erreurs de, tout au plus,\( 0.5\%\) et\( 0.1\%\), respectivement. Utilisez des différentiels pour approximer le pourcentage d'erreur maximal dans la valeur calculée de\( T\).

    Réponse
    \( 0.3\%\)

    44)\( P\) L'alimentation électrique est donnée par\( P=\frac{V^2}{R}\), où\( V\) sont la tension et\( R\) la résistance. Approximation de l'erreur maximale en pourcentage dans le calcul de la puissance si elle\( 120 V\) est appliquée à une\( 2000−Ω\) résistance et des erreurs en pourcentage possibles lors de la mesure\( V\)\( 3\%\) et\( R\) sont et\( 4\%\), respectivement.

    Pour les exercices 45 à 49, trouvez l'approximation linéaire de chaque fonction au point indiqué.

    45)\( f(x,y)=x\sqrt{y},\quad P(1,4)\)

    Réponse
    \( L(x,y) = 2x+\frac{1}{4}y−1\)

    46)\( f(x,y)=e^x\cos y;\quad P(0,0)\)

    47)\( f(x,y)=\arctan(x+2y),\quad P(1,0)\)

    Réponse
    \( L(x,y) = \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}\)

    48)\( f(x,y)=\sqrt{20−x^2−7y^2},\quad P(2,1)\)

    49)\( f(x,y,z)=\sqrt{x^2+y^2+z^2},\quad P(3,2,6)\)

    Réponse
    \( L(x,y,z) = \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z\)

    50) [T] Trouvez l'équation du plan tangent à la surface\( f(x,y)=x^2+y^2\) au point\( (1,2,5),\) et tracez graphiquement la surface et le plan tangent au point.

    51) [T] Trouvez l'équation du plan tangent à la surface au point indiqué et tracez la surface et le plan tangent :\( z=\ln(10x^2+2y^2+1),\quad P(0,0,0).\)

    Réponse

    \( z=0\)

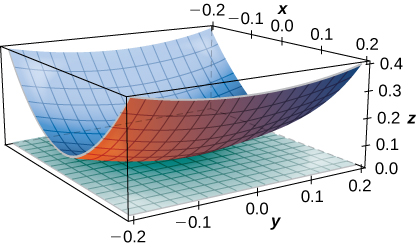
    Surface représentant la fonction z=ln (10x^2+2y^2+1) et son plan tangent au point (0, 0)

    52) [T] Trouvez l'équation du plan tangent à la surface\( z=f(x,y)=\sin(x+y^2)\) au point\( \left(\frac{π}{4},0,\frac{\sqrt{2}}{2}\right)\) et tracez la surface et le plan tangent.

    Contributeurs