16.3E : Exercices pour la section 16.3

Last updated
Save as PDF

Page ID: 197852

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Vrai ou faux ? Si le champ vectoriel$\vecs F$ est conservateur sur la région ouverte et connectée$D$, les intégrales de ligne de$\vecs F$ sont indépendantes du chemin$D$, quelle que soit la forme de$D$.

Réponse: Vrai

2. Vrai ou faux ? La fonction$\vecs r(t)=\vecs a+t(\vecs b−\vecs a)$$0≤t≤1$, où, paramètre le segment de ligne droite de$\vecs a$ à$\vecs b$.

Réponse: Vrai

3. Vrai ou faux ? $\vecs F(x,y,z)=(y\sin z)\,\mathbf{\hat i}+(x\sin z)\,\mathbf{\hat j}+(xy\cos z)\,\mathbf{\hat k}$Le champ vectoriel est conservateur.

Réponse: Vrai

4. Vrai ou faux ? $\vecs F(x,y,z)=y\,\mathbf{\hat i}+(x+z)\,\mathbf{\hat j}−y\,\mathbf{\hat k}$Le champ vectoriel est conservateur.

5. Justifiez le théorème fondamental des intégrales linéaires$\displaystyle \int _C\vecs F·d\vecs r$ dans le cas où$\vecs{F}(x,y)=(2x+2y)\,\mathbf{\hat i}+(2x+2y)\,\mathbf{\hat j}$ et$C$ est une partie du cercle orienté positivement$x^2+y^2=25$ de$(5, 0)$ à$(3, 4).$

Réponse: $\displaystyle \int _C \vecs F·d\vecs r=24$unités de travail

6. [T] Détermine$\displaystyle \int _C\vecs F·d\vecs r,$ où$\vecs{F}(x,y)=(ye^{xy}+\cos x)\,\mathbf{\hat i}+\left(xe^{xy}+\frac{1}{y^2+1}\right)\,\mathbf{\hat j}$ et$C$ représente une portion de la courbe$y=\sin x$ allant de$x=0$ à$x=\frac{π}{2}$.

7. [T] Évaluez l'intégrale de la ligne$\displaystyle \int _C\vecs F·d\vecs r$$\vecs{F}(x,y)=(e^x\sin y−y)\,\mathbf{\hat i}+(e^x\cos y−x−2)\,\mathbf{\hat j}$, où et$C$ est le chemin donné par$\vecs r(t)=(t^3\sin\frac{πt}{2})\,\mathbf{\hat i}−(\frac{π}{2}\cos(\frac{πt}{2}+\frac{π}{2}))\,\mathbf{\hat j}$ for$0≤t≤1$.

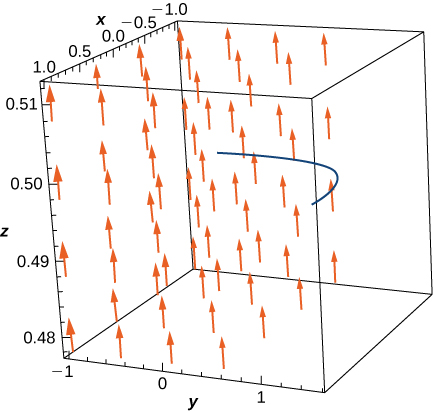
$CNX_Calc_Figure_16_03_201.jpg$

Réponse: $\displaystyle \int _C\vecs F·d\vecs r=\left(e−\frac{3π}{2}\right)$unités de travail

Pour les exercices suivants, déterminez si le champ vectoriel est conservateur et, dans l'affirmative, déterminez la fonction potentielle.

8. $\vecs{F}(x,y)=2xy^3\,\mathbf{\hat i}+3y^2x^2\,\mathbf{\hat j}$

9. $\vecs{F}(x,y)=(−y+e^x\sin y)\,\mathbf{\hat i}+((x+2)e^x\cos y)\,\mathbf{\hat j}$

Réponse: Pas conservateur

10. $\vecs{F}(x,y)=(e^{2x}\sin y)\,\mathbf{\hat i}+(e^{2x}\cos y)\,\mathbf{\hat j}$

11. $\vecs{F}(x,y)=(6x+5y)\,\mathbf{\hat i}+(5x+4y)\,\mathbf{\hat j}$

Réponse: Conservateur,$f(x,y)=3x^2+5xy+2y^2+k$

12. $\vecs{F}(x,y)=(2x\cos(y)−y\cos(x))\,\mathbf{\hat i}+(−x^2\sin(y)−\sin(x))\,\mathbf{\hat j}$

13. $\vecs{F}(x,y)=(ye^x+\sin(y))\,\mathbf{\hat i}+(e^x+x\cos(y))\,\mathbf{\hat j}$

Réponse: Conservateur,$f(x,y)=ye^x+x\sin(y)+k$

Pour les exercices suivants, évaluez les intégrales linéaires à l'aide du théorème fondamental des intégrales linéaires.

14. $\displaystyle ∮_C(y\,\mathbf{\hat i}+x\,\mathbf{\hat j})·d\vecs r,$où se$C$ trouve n'importe quel chemin allant de$(0, 0)$ à$(2, 4)$

15. $\displaystyle ∮_C(2y\,dx+2x\,dy),$où se$C$ trouve le segment de ligne allant de$(0, 0)$ à$(4, 4)$

Réponse: $\displaystyle ∮_C(2y\,dx+2x\,dy)=32$unités de travail

16. [T]$\displaystyle ∮_C\left[\arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}\right]\,dx+\left[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)\right]\,dy$, où se$C$ trouve toute courbe lisse comprise entre$(1, 1)$ et$(−1,2).$

17. Trouvez le champ vectoriel conservateur pour la fonction potentielle$f(x,y)=5x^2+3xy+10y^2.$

Réponse: $\vecs{F}(x,y)=(10x+3y)\,\mathbf{\hat i}+(3x+20y)\,\mathbf{\hat j}$

Pour les exercices suivants, déterminez si le champ vectoriel est conservateur et, dans l'affirmative, trouvez une fonction potentielle.

18. $\vecs{F}(x,y)=(12xy)\,\mathbf{\hat i}+6(x^2+y^2)\,\mathbf{\hat j}$

19. $\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}$

Réponse: $\vecs F$n'est pas conservateur.

20. $\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}$

21. $\vecs F(x,y,z)=(ye^z)\,\mathbf{\hat i}+(xe^z)\,\mathbf{\hat j}+(xye^z)\,\mathbf{\hat k}$

Réponse: $\vecs F$est conservatrice et une fonction potentielle l'est$f(x,y,z)=xye^z+k$.

22. $\vecs F(x,y,z)=(\sin y)\,\mathbf{\hat i}−(x\cos y)\,\mathbf{\hat j}+\,\mathbf{\hat k}$

23. $\vecs F(x,y,z)=\dfrac{1}{y}\,\mathbf{\hat i}-\dfrac{x}{y^2}\,\mathbf{\hat j}+(2z−1)\,\mathbf{\hat k}$

Réponse: $\vecs F$est conservatrice et une fonction potentielle est$f(x,y,z)=\dfrac{x}{y}+z^2-z+k.$

24. $\vecs F(x,y,z)=3z^2\,\mathbf{\hat i}−\cos y\,\mathbf{\hat j}+2xz\,\mathbf{\hat k}$

25. $\vecs F(x,y,z)=(2xy)\,\mathbf{\hat i}+(x^2+2yz)\,\mathbf{\hat j}+y^2\,\mathbf{\hat k}$

Réponse: $\vecs F$est conservatrice et une fonction potentielle est$f(x,y,z)=x^2y+y^2z+k.$

Pour les exercices suivants, déterminez si le champ vectoriel donné est conservateur et trouvez une fonction potentielle.

26. $\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}$

27. $\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+(x^2e^{x^2y})\,\mathbf{\hat j}$

Réponse: $\vecs F$est conservatrice et une fonction potentielle est$f(x,y)=e^{x^2y}+k$

Pour les exercices suivants, évaluez l'intégrale à l'aide du théorème fondamental des intégrales linéaires.

28. Évaluez$\displaystyle \int _C\vecs ∇f·d\vecs r$, où$f(x,y,z)=\cos(πx)+\sin(πy)−xyz$ et où$C$ se trouve tout chemin qui commence$(1,12,2)$ et se termine à$(2,1,−1)$.

29. [T] Évaluez$\displaystyle \int _C\vecs ∇f·d\vecs r$, où$f(x,y)=xy+e^x$ et$C$ est une ligne droite allant de$(0,0)$ à$(2,1)$.

Réponse: $\displaystyle \int _C\vecs F·d\vecs r=\left(e^2+1\right)$unités de travail

30. [T] Évaluez$\displaystyle \int _C\vecs ∇f·d\vecs r,$ où$f(x,y)=x^2y−x$ et$C$ se trouve n'importe quelle trajectoire dans un plan compris entre (1, 2) et (3, 2).

31. Évaluez$\displaystyle \int _C\vecs ∇f·d\vecs r,$ où$f(x,y,z)=xyz^2−yz$ et$C$ a le point initial$(1, 2, 3)$ et le point terminal$(3, 5, 2).$

Réponse: $\displaystyle \int _C\vecs F·d\vecs r=38$unités de travail

Pour les exercices suivants, soit$\vecs{F}(x,y)=2xy^2\,\mathbf{\hat i}+(2yx^2+2y)\,\mathbf{\hat j}$ et$G(x,y)=(y+x)\,\mathbf{\hat i}+(y−x)\,\mathbf{\hat j}$$C_1$ soit la courbe constituée du cercle de rayon 2, centré à l'origine et orienté dans le sens antihoraire, et$C_2$ soit la courbe constituée d'un segment de droite allant de$(0, 0)$ à$(1, 1)$ suivi d'un segment de ligne allant de$(1, 1)$ à$(3, 1).$

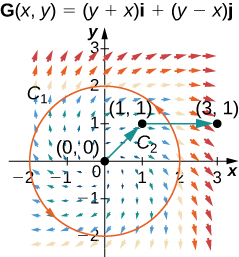
$CNX_Calc_Figure_16_03_203.jpg$

32. Calculez l'intégrale linéaire de$\vecs F$ plus$C_1$.

33. Calculez l'intégrale linéaire de$\vecs G$ plus$C_1$.

Réponse: $\displaystyle ∮_{C_1}\vecs G·d\vecs r=−8π$unités de travail

34. Calculez l'intégrale linéaire de$\vecs F$ plus$C_2$.

35. Calculez l'intégrale linéaire de$\vecs G$ plus$C_2$.

Réponse: $\displaystyle ∮_{C_2}\vecs F·d\vecs r=7$unités de travail

36. [T] Laissez$\vecs F(x,y,z)=x^2\,\mathbf{\hat i}+z\sin(yz)\,\mathbf{\hat j}+y\sin(yz)\,\mathbf{\hat k}$. Calculez$\displaystyle ∮_C\vecs F·d\vecs{r}$, où$C$ se trouve un chemin allant de$A=(0,0,1)$ à$B=(3,1,2)$.

37. [T] Trouver l'intégrale linéaire$\displaystyle ∮_C\vecs F·dr$ du champ vectoriel$\vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k}$ le long de la courbe$C$ paramétrée par$\vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+t\cos(πt),1≤t≤4.$

Réponse: $\displaystyle \int _C\vecs F·d\vecs r=150$unités de travail

Pour les exercices 38 à 40, montrez que les champs vectoriels suivants sont conservateurs. Calculez ensuite$\displaystyle \int _C\vecs F·d\vecs r$ pour la courbe donnée.

38. $\vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}$;$C$ est la courbe composée de segments de droite allant de$(1,1)$ à$(0,2)$ à$(3,0).$

39. $\vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}$;$C$ est paramétré par$x=t^3−1,\;y=t^6−t$, pour$0≤t≤1.$

Réponse: $\displaystyle \int _C\vecs F·d\vecs r=−1$unités de travail

40. [T]$\vecs{F}(x,y)=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}$ ;$C$ est la courbe$\langle e^t,e^{t+1}\rangle,$ de$−1≤t≤0$.

41. La masse de la Terre est$6×10^{27}g$ d'environ 330 000 fois celle du Soleil et 330 000 fois plus. La constante gravitationnelle est$6.7×10^{−8}cm^3/s^2·g$. La distance entre la Terre et le Soleil est d'environ$1.5×10^{12}cm$. Calculez, approximativement, le travail nécessaire pour augmenter la distance entre la Terre et le Soleil de$1\;cm$.

Réponse: $4×10^{31}$erg

42. [T] Laissez$\vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}$. Évaluez l'intégrale$\displaystyle \int _C\vecs F·d\vecs r$, où$\vecs r(t)=\langle\sqrt{t},t^3,e^{\sqrt{t}}\rangle,$$0≤t≤1.$

43. [T]$C:[1,2]→ℝ^2$ Laissez-vous donner par$x=e^{t−1},y=\sin\left(\frac{π}{t}\right)$. Utilisez un ordinateur pour calculer l'intégrale$\displaystyle \int _C\vecs F·d\vecs r=\int _C 2x\cos y\,dx−x^2\sin y\,dy$, où$\vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.$

Réponse: $\displaystyle \int _C\vecs F·d\vecs s=0.4687$unités de travail

44. [T] Utilisez un système d'algèbre informatique pour déterminer la masse d'un fil qui se trouve le long de la courbe$\vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k},$ où$0≤t≤1$, si la densité est donnée par$d(t) = \dfrac{3}{2}t$.

45. Déterminez la circulation et le flux du champ$\vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}$ autour et à travers le trajet semi-circulaire fermé qui consiste en un arc en plein cintre$\vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π$, suivi d'un segment de ligne$\vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.$

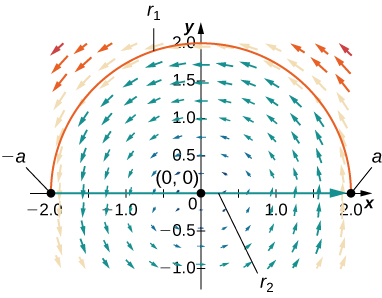
$CNX_Calc_Figure_16_03_204.jpg$

Réponse: $\text{circulation}=πa^2$et$\text{flux}=0$

46. Calculez$\displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy,$ où$\vecs r(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.$

47. Complétez la preuve du théorème intitulé THE PATH INDEPENDENCE TEST FOR CONSERVATIVE FIELDS en démontrant que$f_y=Q(x,y).$

Contributeurs

Template:contribopenstaxcalc