16.3 : Champs vectoriels conservateurs

Objectifs d'apprentissage

• Décrivez des courbes simples et fermées ; définissez des régions connectées et simplement connectées.
• Expliquer comment trouver une fonction potentielle pour un champ vectoriel conservateur.
• Utilisez le théorème fondamental des intégrales linéaires pour évaluer une intégrale linéaire dans un champ vectoriel.
• Expliquer comment tester un champ vectoriel pour déterminer s'il est conservateur.

Dans cette section, nous poursuivons l'étude des champs vectoriels conservateurs. Nous examinons le théorème fondamental des intégrales linéaires, qui est une généralisation utile du théorème fondamental du calcul aux intégrales linéaires de champs vectoriels conservateurs. Nous découvrons également comment tester si un champ vectoriel donné est conservateur et comment construire une fonction potentielle pour un champ vectoriel connu pour être conservateur.

Courbes et régions

Avant de poursuivre notre étude des champs vectoriels conservateurs, nous avons besoin de quelques définitions géométriques. Les théorèmes des sections suivantes reposent tous sur l'intégration de certains types de courbes et de régions. Nous développons donc les définitions de ces courbes et régions ici. Nous définissons d'abord deux types particuliers de courbes : les courbes fermées et les courbes simples. Comme nous l'avons appris, une courbe fermée est une courbe qui commence et se termine au même point. Une courbe simple est une courbe qui ne se croise pas. Une courbe à la fois fermée et simple est une courbe fermée simple (Figure\(\PageIndex{1}\)).

Chiffre\(\PageIndex{1}\). Types de courbes simples ou non simples et fermées ou non fermées.

DÉFINITION : Courbes fermées

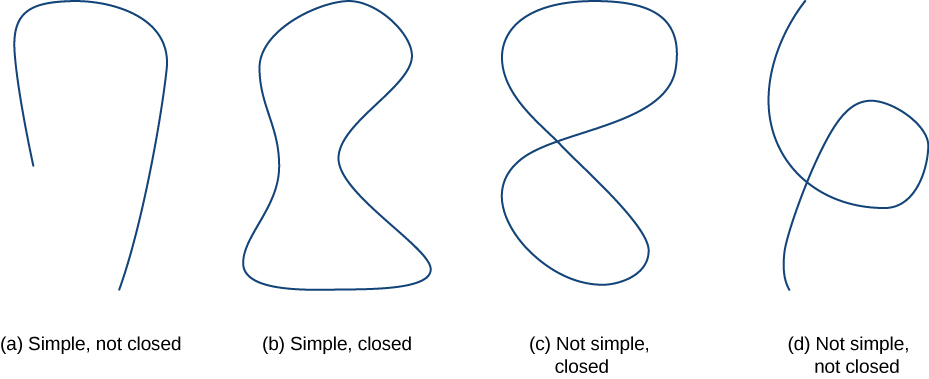
\(C\)La courbe est une courbe fermée s'il existe un paramétrage\(\vecs r(t)\),\(a≤t≤b\) de\(C\) sorte que le paramétrage traverse la courbe exactement une fois et\(\vecs r(a)=\vecs r(b)\). \(C\)La courbe est une courbe simple si\(C\) elle ne se croise pas. C'est-à-dire que\(C\) c'est simple s'il existe un paramétrage\(\vecs r(t)\),\(a≤t≤b\)\(\vecs r\) c'est-à-dire un à un\((a,b)\).\(C\) C'est possible pour\(\vecs r(a)=\vecs r(b)\), ce qui signifie que la courbe simple est également fermée.

Exemple\(\PageIndex{1}\): Determining Whether a Curve Is Simple and Closed

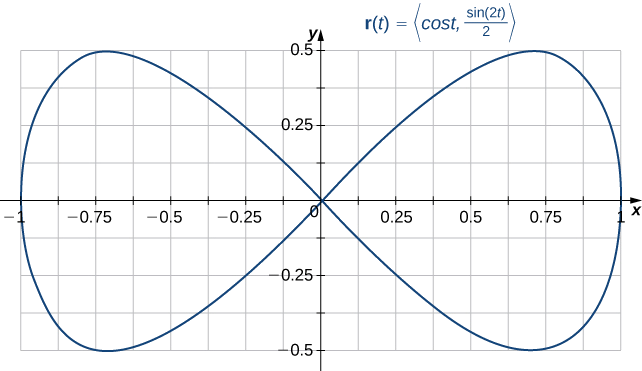
La courbe avec paramétrage\(\vecs{r}(t)=\left\langle\cos t,\frac{\sin(2t)}{2}\right\rangle\) est-elle\(0≤t≤2\pi\) une simple courbe fermée ?

Solution

Notez que\(\vecs{r}(0)=⟨1,0⟩=\vecs r(2\pi)\), par conséquent, la courbe est fermée. La courbe n'est cependant pas simple. Pour voir cela, notez que\(\vecs{r}\left(\frac{\pi}{2}\right)=⟨0,0⟩=\vecs{r}\left(\frac{3\pi}{2}\right)\), et donc la courbe se croise à l'origine (Figure\(\PageIndex{2}\)).

Chiffre\(\PageIndex{2}\) . Une courbe fermée mais pas simple.

Exercice\(\PageIndex{1}\)

La courbe est-elle donnée par paramétrage\(\vecs{r}(t)=⟨2\cos t,3\sin t⟩\)\(0≤t≤6\pi\), une simple courbe fermée ?

Allusion

Esquissez la courbe.

Réponse

Oui

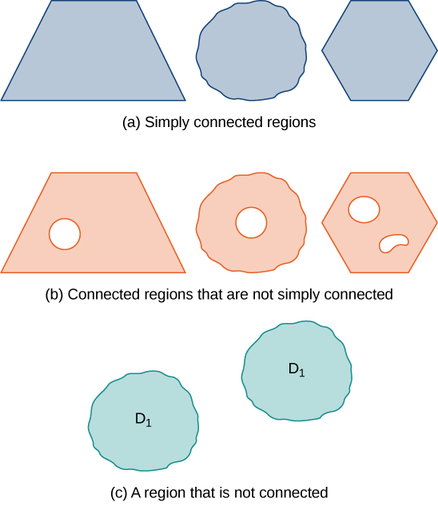
De nombreux théorèmes de ce chapitre relient une intégrale sur une région à une intégrale au-dessus de la limite de la région, où la limite de la région est une simple courbe fermée ou une union de courbes fermées simples. Pour développer ces théorèmes, nous avons besoin de deux définitions géométriques des régions : celle d'une région connectée et celle d'une région simplement connectée. Une région connectée est une région dans laquelle se trouve un chemin qui relie deux points quelconques situés dans cette région. Une région simplement connectée est une région connectée qui ne comporte aucun trou. Ces deux notions, ainsi que la notion de courbe fermée simple, nous permettent d'énoncer plusieurs généralisations du théorème fondamental du calcul plus loin dans le chapitre. Ces deux définitions sont valables pour les régions dans un nombre quelconque de dimensions, mais nous ne nous intéressons qu'aux régions à deux ou trois dimensions.

DÉFINITION : régions connectées

Une région D est une région connectée si, pour deux points\(P_1\) et\(P_2\), il existe un chemin allant de\(P_1\) à\(P_2\) avec une trace entièrement contenue à l'intérieur de D. Une région D est une région simplement connectée si D est connecté pour n'importe quelle courbe fermée C simple située à l'intérieur de D, et la courbe C peut être réduite continuellement jusqu'à un point tout en restant entièrement à l'intérieur de D. En deux dimensions, une région est simplement connectée si elle est connectée et ne comporte aucun trou.

Toutes les régions simplement connectées sont connectées, mais toutes les régions connectées ne sont pas simplement connectées (Figure\(\PageIndex{3}\)).

Figure\(\PageIndex{3}\) : Les régions connectées ne sont pas toutes simplement connectées. (a) Les régions simplement connectées ne présentent pas de trous. (b) Les régions connectées qui ne sont pas simplement connectées peuvent comporter des trous, mais vous pouvez toujours trouver un chemin dans la région entre deux points quelconques. (c) Une région qui n'est pas connectée possède certains points qui ne peuvent pas être reliés par un chemin dans la région.

Exercice\(\PageIndex{2}\)

La région de l'image ci-dessous est-elle connectée ? La région est-elle simplement connectée ?

Allusion

Examinez les définitions.

Réponse

La région de la figure est connectée. La région de la figure n'est pas simplement connectée.

Théorème fondamental pour les intégrales linéaires

Maintenant que nous avons compris certaines courbes et régions de base, généralisons le théorème fondamental du calcul aux intégrales linéaires. Rappelons que le théorème fondamental du calcul dit que si une fonction\(f\) a une antidérivée\(F\), alors l'intégrale\(f\) de\(a\) à\(b\) dépend uniquement des valeurs de\(F\) at\(a\) et at,\(b\) c'est-à-dire

\[\int_a^bf(x)\,dx=F(b)−F(a). \nonumber \]

Si nous considérons le gradient comme une dérivée, le même théorème vaut pour les intégrales de lignes vectorielles. Nous montrons comment cela fonctionne à l'aide d'un exemple de motivation.

Exemple\(\PageIndex{2}\): Evaluating a Line Integral and the Antiderivatives of the Endpoints

Laissez\(\vecs{F}(x,y)=⟨2x,4y⟩\). Calculez\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), où C est le segment de droite de\((0,0)\) à\((2,2)\) (Figure\(\PageIndex{4}\)).

Solution

Nous utilisons la méthode de la section précédente pour calculer\(\int_C \vecs{F} \cdot d\vecs{r}\). La courbe C peut être paramétrée par\(\vecs{r}(t)=⟨2t,2t⟩\),\(0≤t≤1\). Ensuite,\(\vecs{F}(\vecs r(t))=⟨4t,8t⟩\) et\(\vecs r′(t)=⟨2,2⟩\), ce qui implique que

\[\begin{align*} \int_C \vecs{F}·d\vecs{r} &=\int_0^1⟨4t,8t⟩·⟨2,2⟩dt \\[4pt] &=\int_0^1(8t+16t)dt=\int_0^1 24tdt\\[4pt] &={\big[12t^2\big]}_0^1=12. \end{align*}\]

Figure\(\PageIndex{4}\) : La valeur de l'intégrale droite\(\int_C \vecs{F} \cdot d\vecs{r}\) dépend uniquement de la valeur de la fonction potentielle de aux\(\vecs{F}\) extrémités de la courbe.

Remarquez que\(\vecs{F}=\vecs \nabla f\), où\(f(x,y)=x^2+2y^2\). Si nous considérons le gradient comme un dérivé, alors\(f\) est un « antidérivé » de\(\vecs{F}\). Dans le cas d'intégrales à variable unique, l'intégrale de la dérivée\(g′(x)\) est\(g(b)−g(a)\), où a est le point de départ de l'intervalle d'intégration et b est le point final. Si les intégrales de lignes vectorielles fonctionnent comme des intégrales à variable unique, nous pouvons nous attendre\(\vecs{F}\) à ce que l'intégrale soit\(f(P_1)−f(P_0)\), où se\(P_1\) trouve l'extrémité de la courbe d'intégration et\(P_0\) le point de départ. Notez que c'est le cas pour cet exemple :

\[\int_C \vecs{F} \cdot d\vecs{r}=\int_C \vecs \nabla f \cdot d\vecs{r}=12 \nonumber \]

et

\[f(2,2)−f(0,0)=4+8−0=12. \nonumber \]

En d'autres termes, l'intégrale d'une « dérivée » peut être calculée en évaluant une « antidérivée » aux extrémités de la courbe et en la soustrayant, comme pour les intégrales à variable unique.

Le théorème suivant indique que, dans certaines conditions, ce qui s'est passé dans l'exemple précédent vaut pour n'importe quel champ de gradient. Le même théorème vaut pour les intégrales de lignes vectorielles, que nous appelons le théorème fondamental des intégrales de lignes.

Théorème : LE THÉORÈME FONDAMENTAL DES INTÉGRALES LINÉAIRES

Soit C une courbe lisse par morceaux avec paramétrage\(\vecs r(t)\),\(a≤t≤b\). \(f\)Soit une fonction de deux ou trois variables avec des dérivées partielles du premier ordre qui existent et sont continues sur C. Ensuite,

\[\int_C \vecs \nabla f \cdot d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \label{FunTheLine} \]

Une preuve

Tout d'abord,

\[\int_C \vecs \nabla f \cdot d \vecs{r}=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)\,dt. \nonumber \]

Selon la règle de la chaîne,

\[\dfrac{d}{dt}(f( \vecs r(t))= \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t) \nonumber \]

Par conséquent, selon le théorème fondamental du calcul,

\[\begin{align*} \int_C \vecs \nabla f \cdot d \vecs{r} &=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)dt \\[4pt] &=\int_a^b\dfrac{d}{dt}(f( \vecs r(t))dt \\[4pt] &={\big[f( \vecs r(t))\big]}_{t=a}^{t=b}\\[4pt] &=f( \vecs r(b))−f( \vecs r(a)). \end{align*}\]

\(\square\)

Nous savons que s'il s'\(\vecs{F}\)agit d'un champ vectoriel conservateur, il existe une fonction potentielle\(f\) telle que\( \vecs \nabla f= \vecs F\). Par conséquent

\[\int_C \vecs F·d\vecs r=\int_C\vecs \nabla f·d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]

En d'autres termes, tout comme pour le théorème fondamental du calcul, le calcul de l'intégrale linéaire\(\int_C \vecs F·d\vecs{r}\), où\(\vecs{F}\) est conservatrice, se fait en deux étapes :

1. Trouver une fonction potentielle (« antidérivée »)\(f\) pour\(\vecs{F}\) et
2. Calculez la valeur de aux\(f\) extrémités de\(C\) et calculez leur différence\(f(\vecs r(b))−f(\vecs r(a))\).

Gardez toutefois à l'esprit qu'il existe une différence majeure entre le théorème fondamental du calcul et le théorème fondamental des intégrales linéaires :
une fonction d'une variable continue doit avoir une antidérivée. Cependant, un champ vectoriel, même s'il est continu, n'a pas besoin de fonction potentielle.

Exemple\(\PageIndex{3}\): Applying the Fundamental Theorem

Calculer\(\int_C \vecs{F} \cdot d\vecs{r}\) l'intégrale, où\(\vecs{F}(x,y,z)=⟨2x\ln y,\dfrac{x^2}{y}+z^2,2yz⟩\) et\(C\) est une courbe avec paramétrage\(\vecs{r}(t)=⟨t^2,t,t⟩\),\(1≤t≤e\)

1. sans utiliser le théorème fondamental des intégrales linéaires et
2. en utilisant le théorème fondamental des intégrales linéaires.

Solution

1. Tout d'abord, calculons l'intégrale sans le théorème fondamental pour les intégrales linéaires et utilisons plutôt la méthode que nous avons apprise dans la section précédente :

\[\begin{align*} \int_C \vecs{F} \cdot dr &=\int_1^e\vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt\\[4pt] &=\int_1^e⟨2t^2\ln t,\dfrac{t^4}{t}+t^2,2t^2⟩ \cdot ⟨2t,1,1⟩\,dt\\[4pt] &=\int_1^e(4t^3\ln t+t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t \,dt+\int_1^e(t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t\,dt+{\Big[\dfrac{t^4}{4}+t^3\Big]}_1^e \\[4pt] &=\int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{1}{4} −1 \\[4pt] &= \int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{5}{4}\end{align*}\]

Integral\(\displaystyle \int_1^e t^3\ln t\,dt\) nécessite une intégration par pièces. Laissez\(u=\ln t\) et\(dv=t^3\). Ensuite\(u=\ln t\),\(dv=t^3\)

et

\[du=\dfrac{1}{t}\,dt, \;\;v=\dfrac{t^4}{4}.\nonumber \]

Par conséquent,

\[\begin{align*} \int_1^e t^3\ln t\,dt &={\Big[\dfrac{t^4}{4}\ln t\Big]}_1^e−\dfrac{1}{4}\int_1^e t^3\,dt \\[4pt] &=\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right). \end{align*}\]

Ainsi,

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &= 4\int_1^e t^3\ln t\, dt\quad +\quad \dfrac{e^4}{4}+e^3 − \dfrac{5}{4} \\[4pt] &=4\left(\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right)\right)+\dfrac{e^4}{4}+e^3−\dfrac{5}{4}\\[4pt] &=e^4−\dfrac{e^4}{4}+\dfrac{1}{4}+\dfrac{e^4}{4}+e^3−\dfrac{5}{4} \\[4pt] &=e^4+e^3−1. \end{align*}\]

2. Étant donné qu'il\(f(x,y,z)=x^2\ln y+yz^2\) s'agit d'une fonction potentielle pour\(\vecs F\), utilisons le théorème fondamental des intégrales linéaires pour calculer l'intégrale. Notez que

\[\begin{align*} \int_C \vecs F \cdot d\vecs{r} &=\int_C \vecs \nabla f \cdot d\vecs{r} \\[4pt] &=f(\vecs r(e))−f(\vecs r(1)) \\[4pt] &=f(e^2,e,e)−f(1,1,1)\\[4pt] &=e^4+e^3−1. \end{align*}\]

Ce calcul est beaucoup plus simple que celui que nous avons fait en (a). Tant que nous avons une fonction potentielle, il est beaucoup plus facile de calculer une intégrale linéaire à l'aide du théorème fondamental pour les intégrales de lignes que de calculer sans le théorème.

L'exemple\(\PageIndex{3}\) illustre une fonctionnalité intéressante du théorème fondamental des intégrales linéaires : il nous permet de calculer plus facilement de nombreuses intégrales de lignes vectorielles. Tant que nous avons une fonction potentielle, le calcul de l'intégrale de la droite consiste uniquement à évaluer la fonction potentielle aux extrémités et à la soustraire.

Exercice\(\PageIndex{3}\)

Étant donné qu'il\(f(x,y)={(x−1)}^2y+{(y+1)}^2x\) s'agit d'une fonction potentielle pour\(\vecs F(x,y)=⟨2xy−2y+{(y+1)}^2,{(x−1)}^2+2yx+2x⟩\), calculez l'intégrale\(\int_C \vecs F·d\vecs r\), où\(C\) est la moitié inférieure du cercle unitaire orientée dans le sens antihoraire.

Allusion

Le théorème fondamental des intervalles de lignes indique que cette intégrale ne dépend que de la valeur aux\(f\) extrémités de\(C\).

Réponse

2

Le théorème fondamental des intégrales linéaires a deux conséquences importantes. La première conséquence est que si elle\(\vecs{F}\) est conservatrice et qu'il s'\(C\)agit d'une courbe fermée, alors la circulation du\(\vecs{F}\) long\(C\) est nulle, c'est-à-dire\(\int_C \vecs F·d\vecs r=0\). Pour voir pourquoi cela est vrai,\(f\) soyons une fonction potentielle pour\(\vecs{F}\). Comme\(C\) il s'agit d'une courbe fermée, le point terminal\(\vecs r(b)\) de\(C\) est le même que l'initiale\(\vecs r(a)\) de\(C\) — c'est-à-dire,\(\vecs r(a)=\vecs r(b)\). Par conséquent, selon le théorème fondamental des intégrales linéaires,

\[\begin{align} \oint_C \vecs F·d\vecs r &=\oint_C \vecs \nabla f·d\vecs r\\[4pt] &=f(\vecs r(b))−f(\vecs r(a)) \\[4pt] &=f(\vecs r(b))−f(\vecs r(b)) \\[4pt] &=0. \end{align} \nonumber \]

Rappelons que si un champ vectoriel conservateur\(\vecs{F}\) est qualifié de « conservateur », c'est parce que ces champs vectoriels modélisent les forces dans lesquelles l'énergie est conservée. Nous avons montré que la gravité est un exemple d'une telle force. Si nous considérons le champ vectoriel\(\vecs{F}\) en entier\(\oint_C \vecs F·d\vecs r\) comme un champ gravitationnel, alors l'équation est la\(\oint_C \vecs{F}·d\vecs{r}=0\) suivante. Si une particule suit un trajet qui commence et se termine au même endroit, alors le travail effectué par gravité sur la particule est nul.

La deuxième conséquence importante du théorème fondamental des intégrales linéaires (équation \ ref {FunTheLine}) est que les intégrales linéaires des champs vectoriels conservateurs sont indépendantes du chemin, c'est-à-dire qu'elles dépendent uniquement des extrémités de la courbe donnée et ne dépendent pas du chemin entre les extrémités.

DÉFINITION : Path Independence

\(\vecs{F}\)Soit un champ vectoriel avec domaine\(D\) ; il est indépendant du chemin (ou indépendant du chemin) si

\[\int_{C_1} \vecs{F}·d\vecs{r}=\int_{C_2} \vecs{F}·d\vecs{r} \nonumber \]

pour tous les chemins\(C_1\) et\(C_2\)\(D\) avec les mêmes points initial et terminal.

La deuxième conséquence est énoncée formellement dans le théorème suivant.

Théorème : CHAMPS CONSERVATEURS

S'il s'\(\vecs{F}\)agit d'un champ vectoriel conservateur, il\(\vecs{F}\) est indépendant du chemin.

Une preuve

\(D\)Dénotons le domaine de\(\vecs{F}\) et laissons\(C_1\) et\(C_2\) être deux chemins\(D\) avec les mêmes points initial et terminal (Figure\(\PageIndex{5}\)). Appelez le point initial\(P_1\) et le point terminal\(P_2\). Puisque\(\vecs{F}\) c'est conservateur, il existe une fonction potentielle\(f\) pour\(\vecs{F}\). Selon le théorème fondamental des intégrales linéaires,

\[\int_{C_1} \vecs{F}·d\vecs{r}=f(P_2)−f(P_1)=\int_{C_2} \vecs{F}·d\vecs{r}. \nonumber \]

Par conséquent,\(\int_{C_1}\vecs F·d\vecs r=\int_{C_2}\vecs F·d\vecs r\) et\(\vecs{F}\) est indépendant du chemin.

\(\square\)

Pour visualiser ce que signifie l'indépendance du sentier, imaginez trois randonneurs montant du camp de base au sommet d'une montagne. Le randonneur 1 emprunte un chemin escarpé directement du camp jusqu'au sommet. Hiker 2 emprunte une route sinueuse qui n'est pas raide du camp au sommet. Le randonneur 3 commence par emprunter la route raide mais à mi-chemin du sommet décide que c'est trop difficile pour lui. Il retourne donc au camp et emprunte le chemin non escarpé qui mène au sommet. Les trois randonneurs empruntent des sentiers dans un champ gravitationnel. Puisque la gravité est une force dans laquelle l'énergie est conservée, le champ gravitationnel est conservateur. Par indépendance du chemin, la quantité totale de travail effectuée par gravité sur chacun des randonneurs est la même car ils ont tous commencé au même endroit et se sont terminés au même endroit. Le travail effectué par les randonneurs inclut d'autres facteurs tels que la friction et les mouvements musculaires, de sorte que la quantité totale d'énergie dépensée par chacun n'est pas la même, mais l'énergie nette dépensée contre la gravité est la même pour les trois randonneurs.

Figure\(\PageIndex{4}\) : Le champ vectoriel est conservateur et donc indépendant de la trajectoire.

Nous avons montré qu'il\(\vecs{F}\) est conservateur, alors il\(\vecs{F}\) est indépendant de la trajectoire. Il s'avère que si le domaine de\(\vecs{F}\) est ouvert et connecté, l'inverse est également vrai. C'est-à-dire qu'il\(\vecs{F}\) est indépendant du chemin et que le domaine de\(\vecs{F}\) est ouvert et connecté, il\(\vecs{F}\) est conservateur. Par conséquent, l'ensemble des champs vectoriels conservateurs sur les domaines ouverts et connectés est précisément l'ensemble des champs vectoriels indépendants du chemin.

Théorème : LE TEST D'INDÉPENDANCE PATH POUR LES DOMAINES CONSERVATEURS

S'il s'\(\vecs{F}\)agit d'un champ vectoriel continu indépendant du chemin et que le domaine\(D\) de\(\vecs{F}\) est ouvert et connecté, alors\(\vecs{F}\) il est conservateur.

Une preuve

Nous prouvons le théorème des champs vectoriels dans\(ℝ^2\). La preuve pour les champs vectoriels\(ℝ^3\) est similaire. Pour montrer que\(\vecs F=⟨P,Q⟩\) c'est conservateur, nous devons trouver une fonction potentielle\(f\) pour\(\vecs{F}\). À cette fin,\(X\) soyons un point fixe\(D\). Quel que soit\((x,y)\) le point d'entrée\(D\),\(C\) soit un chemin allant de\(X\) à\((x,y)\). Définissez\(f(x,y)\) par\(f(x,y)=\int_C \vecs F·d\vecs r\). (Notez que cette définition de n'a de\(f\) sens que parce qu'elle\(\vecs{F}\) est indépendante du chemin. Si ce n'\(\vecs{F}\)était pas indépendant du chemin, il est possible de trouver un autre chemin\(C′\) de\(X\) à\((x,y)\) tel que\(\int_C \vecs F·d\vecs r≠\int_C \vecs F·d\vecs r\), et dans ce cas, ce ne\(f(x,y)\) serait pas une fonction.) Nous voulons montrer qu'il\(f\) possède la propriété\(\vecs \nabla f=\vecs F\).

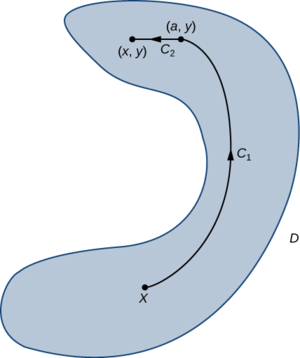
Comme le domaine\(D\) est ouvert, il est possible de trouver un disque centré de\((x,y)\) telle sorte que le disque soit entièrement contenu à l'intérieur\(D\). \(a<x\)Soit\((a,y)\) un point sur ce disque. \(C\)Soyons un chemin de\(X\) à\((x,y)\) qui se compose de deux parties :\(C_1\) et\(C_2\). La première pièce\(C_1\), est n'importe quel chemin allant de\(C\) à\((a,y)\) qui reste à l'intérieur\(D\) ;\(C_2\) est le segment de ligne horizontale allant de\((a,y)\) à\((x,y)\) (Figure\(\PageIndex{6}\)). Alors

\[f(x,y)=\int_{C_1} \vecs F·d\vecs r+\int_{C_2}\vecs F \cdot d\vecs r.\nonumber \]

La première intégrale ne dépend pas de\(x\), donc

\[f_x(x,y)=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Si nous paramétrons\(C_2\) par\(\vecs r(t)=⟨t,y⟩\)\(a≤t≤x\), alors

\[\begin{align*} f_x(x,y) &=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \dfrac{d}{dt}(⟨t,y⟩)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot ⟨1,0⟩\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt.\\[4pt] \end{align*}\]

Selon le théorème fondamental du calcul (partie 1),

\[f_x(x,y)=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt=P(x,y).\nonumber \]

Chiffre\(\PageIndex{6}\). Ici,\(C_1\) c'est tout chemin allant de\(C\) à\((a,y)\) qui reste à l'intérieur\(D\), et\(C_2\) c'est le segment de ligne horizontale allant de\((a,y)\) à\((x,y)\).

Un argument similaire utilisant un segment de ligne verticale plutôt qu'un segment de ligne horizontale le montre\(f_y(x,y)=Q(x,y)\).

Par conséquent\(\vecs \nabla f=\vecs F\), et\(\vecs{F}\) est conservateur.

\(\square\)

Nous avons passé beaucoup de temps à discuter et à prouver les théorèmes ci-dessus, mais nous pouvons les résumer simplement : un champ vectoriel\(\vecs F\) sur un domaine ouvert et connecté est conservateur si et seulement s'il est indépendant du chemin. Il est important de le savoir, car les champs vectoriels conservateurs sont extrêmement importants dans les applications, et ces théorèmes nous offrent une façon différente de voir ce que signifie être conservateur en utilisant l'indépendance de la trajectoire.

Exemple\(\PageIndex{4}\): Showing That a Vector Field Is Not Conservative

Utilisez l'indépendance du chemin pour montrer que le champ vectoriel n'\(\vecs F(x,y)=⟨x^2y,y+5⟩\)est pas conservateur.

Solution

Nous pouvons indiquer que ce n'\(\vecs{F}\)est pas conservateur en montrant que ce n'\(\vecs{F}\)est pas indépendant du chemin. Nous le faisons en donnant deux chemins différents,\(C_1\) et\(C_2\), qui commencent\((0,0)\) et se terminent à\((1,1)\), et pourtant\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\).

\(C_1\)Soit la courbe avec paramétrage\(\vecs r_1(t)=⟨t,\,t⟩\),\(0≤t≤1\) et\(C_2\) soit la courbe avec paramétrage\(\vecs r_2(t)=⟨t,\,t^2⟩\),\(0≤t≤1\) (Figure\(\PageIndex{7}\).). Alors

\[\begin{align*} \int_{C_1} \vecs{F}·d\vecs r &=\int_0^1 \vecs F(\vecs r_1(t))·\vecs r_1′(t)\,dt \\[4pt] &=\int_0^1⟨t^3,t+5⟩·⟨1,1⟩\,dt=\int_0^1(t^3+t+5)\,dt\\[4pt] &={\Big[\dfrac{t^4}{4}+\dfrac{t^2}{2}+5t\Big]}_0^1=\dfrac{23}{4} \end{align*}\]

et

\[\begin{align*} \int_{C_2}\vecs F·d\vecs r &=\int_0^1 \vecs F(\vecs r_2(t))·\vecs r_2′(t)\,dt \\[4pt] &=\int_0^1⟨t^4,t^2+5⟩·⟨1,2t⟩\,dt=\int_0^1(t^4+2t^3+10t)\,dt \\[4pt] &={\Big[\dfrac{t^5}{5}+\dfrac{t^4}{2}+5t^2\Big]}_0^1=\dfrac{57}{10}. \end{align*}\]

Puisque\(\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r\), la valeur d'une intégrale droite de\(\vecs{F}\) dépend du chemin entre deux points donnés. Par conséquent, n'\(\vecs{F}\)est pas indépendant du chemin et n'\(\vecs{F}\)est pas conservateur.

Figure\(\PageIndex{7}\) : Les courbes\(C_1\)\(C_2\) sont toutes deux orientées de gauche à droite.

Exercice\(\PageIndex{4}\)

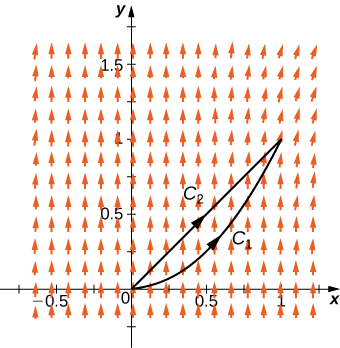
Montrez que cela n'\(\vecs{F}(x,y)=⟨xy,\,x^2y^2⟩\)est pas indépendant du chemin en considérant le segment de droite allant de\((0,0)\) à\((0,2)\) et la partie du\(y=\dfrac{x^2}{2}\) graphique allant de\((0,0)\) à\((0,2)\).

Allusion

Calculez les intégrales de ligne correspondantes.

Réponse

Si\(C_1\) et\(C_2\) représentez les deux courbes, alors\[\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r. \nonumber \]

Champs vectoriels conservateurs et fonctions potentielles

Comme nous l'avons appris, le théorème fondamental des intégrales linéaires indique que s'il\(\vecs{F}\) est conservateur, le calcul\(\int_C \vecs F·d\vecs r\) comporte deux étapes : d'abord, trouver une fonction potentielle\(f\) pour\(\vecs{F}\) et, deuxièmement, calculer\(f(P_1)−f(P_0)\), où\(P_1\) est le point final de\(C\) et\(P_0\) est le point de départ. Pour utiliser ce théorème pour un champ conservateur\(\vecs{F}\), nous devons être en mesure de trouver une fonction potentielle\(f\) pour\(\vecs{F}\). Nous devons donc répondre à la question suivante : Dans un champ vectoriel conservateur\(\vecs{F}\), comment trouver une fonction\(f\) telle que\(\vecs \nabla f=\vecs{F}\) ? Avant de donner une méthode générale pour trouver une fonction potentielle, motivons-la avec un exemple.

Exemple\(\PageIndex{5}\): Finding a Potential Function

Trouvez une fonction potentielle pour\(\vecs F(x,y)=⟨2xy^3,3x^2y^2+\cos(y)⟩\), montrant ainsi qu'elle\(\vecs{F}\) est conservatrice.

Solution

Supposons que ce\(f(x,y)\) soit une fonction potentielle pour\(\vecs{F}\). Alors\(\vecs \nabla f=\vecs F\), et donc

\[f_x(x,y)=2xy^3 \; \; \text{and} \;\; f_y(x,y)=3x^2y^2+\cos y. \nonumber \]

L'intégration de l'équation\(f_x(x,y)=2xy^3\) par rapport à\(x\) donne l'équation

\[f(x,y)=x^2y^3+h(y). \nonumber \]

Notez que puisque nous intégrons une fonction à deux variables par rapport à\(x\), nous devons ajouter une constante d'intégration qui est une constante par rapport à\(x\), mais qui peut toujours être fonction de\(y\). L'équation\(f(x,y)=x^2y^3+h(y)\) peut être confirmée en prenant la dérivée partielle par rapport à\(x\) :

\[\dfrac{∂f}{∂x}=\dfrac{∂}{∂x}(x^2y^3)+\dfrac{∂}{∂x}(h(y))=2xy^3+0=2xy^3. \nonumber \]

Comme\(f\) c'est une fonction potentielle pour\(\vecs{F}\),

\[f_y(x,y)=3x^2y^2+\cos(y), \nonumber \]

et donc

\[3x^2y^2+g′(y)=3x^2y^2+\cos(y). \nonumber \]

Cela implique que\(h′(y)=\cos y\), donc\(h(y)=\sin y+C\). Par conséquent, toute fonction du formulaire\(f(x,y)=x^2y^3+\sin(y)+C\) est une fonction potentielle. La prise, en particulier,\(C=0\) donne la fonction potentielle\(f(x,y)=x^2y^3+\sin(y)\).

Pour vérifier qu'il\(f\) s'agit d'une fonction potentielle, notez que\(\vecs \nabla f(x,y)=⟨2xy^3,3x^2y^2+\cos y⟩=\vecs F\).

Exercice\(\PageIndex{5}\)

Trouvez une fonction potentielle pour\(\vecs{F}(x,y)=⟨e^xy^3+y,3e^xy^2+x⟩\).

Allusion

Suivez les étapes de l'exemple\(\PageIndex{5}\).

Réponse

\(f(x,y)=e^xy^3+xy\)

La logique de l'exemple précédent s'étend à la recherche de la fonction potentielle pour tout champ vectoriel conservateur dans\(ℝ^2\). Nous avons donc la stratégie de résolution de problèmes suivante pour trouver des fonctions potentielles :

STRATÉGIE DE RÉSOLUTION DE PROBLÈMES : RECHERCHE D'UNE FONCTION POTENTIELLE POUR UN CHAMP VECTORIEL CONSERVATEUR\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\)

1. Intégrez\(P\) par rapport à\(x\). Il en résulte une fonction de la forme\(g(x,y)+h(y)\), où\(h(y)\) est inconnue.
2. Prenez la dérivée partielle\(g(x,y)+h(y)\) de par rapport à\(y\), qui donne la fonction\(gy(x,y)+h′(y)\).
3. Utilisez l'équation\(gy(x,y)+h′(y)=Q(x,y)\) pour trouver\(h′(y)\).
4. Intégrez\(h′(y)\) pour trouver\(h(y)\).
5. Toute fonction de la forme\(f(x,y)=g(x,y)+h(y)+C\), où\(C\) est une constante, est une fonction potentielle pour\(\vecs{F}\).

Nous pouvons adapter cette stratégie pour trouver des fonctions potentielles pour les champs vectoriels dans\(ℝ^3\), comme le montre l'exemple suivant.

Exemple\(\PageIndex{6}\): Finding a Potential Function in \(ℝ^3\)

Trouvez une fonction potentielle pour\(F(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩\), montrant ainsi qu'elle\(\vecs{F}\) est conservatrice.

Solution

Supposons qu'il\(f\) s'agisse d'une fonction potentielle. Alors,\(\vecs \nabla f= \vecs{F}\) et donc\(f_x(x,y,z)=2xy\). L'intégration de cette équation par rapport à\(x\) donne l'équation\(f(x,y,z)=x^2y+g(y,z)\) pour certaines fonctions\(g\). Notez que, dans ce cas, la constante d'intégration par rapport à\(x\) est fonction de\(y\) et\(z\).

Comme il\(f\) s'agit d'une fonction potentielle,

\[x^2+2yz^3=f_y(x,y,z)=x^2+g_y(y,z). \nonumber \]

Par conséquent,

\[g_y(y,z)=2yz^3. \nonumber \]

Intégrer cette fonction en termes de\(y\) rendements

\[g(y,z)=y^2z^3+h(z) \nonumber \]

pour une fonction\(h(z)\) quelconque ou\(z\) seul. (Notez que, parce que nous savons que\(g\) c'est une fonction de\(y\) et\(z\), que nous n'avons pas besoin d'écrire\(g(y,z)=y^2z^3+h(x,z)\).) Par conséquent,

\[f(x,y,z)=x^2y+g(y,z)=x^2y+y^2z^3+h(z). \nonumber \]

Pour le trouver\(f\), il ne nous reste plus qu'à trouver\(h\). Comme il\(f\) s'agit d'une fonction potentielle,

\[3y^2z^2+2z=g_z(y,z)=3y^2z^2+h′(z). \nonumber \]

Cela implique que\(h′(z)=2z\), donc\(h(z)=z^2+C\). La location\(C=0\) donne la fonction potentielle

\[f(x,y,z)=x^2y+y^2z^3+z^2. \nonumber \]

Pour vérifier qu'il\(f\) s'agit d'une fonction potentielle, notez que\(\vecs \nabla f(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩=\vecs F(x,y,z)\).

Exercice\(\PageIndex{6}\)

Trouvez une fonction potentielle pour\(\vecs{F}(x,y,z)=⟨12x^2,\cos y\cos z,1−\sin y\sin z⟩\).

Allusion

Exemple suivant\(\PageIndex{6}\), commencez par intégrer par rapport à\(x\).

Réponse

\(f(x,y,z)=4x^3+\sin y\cos z+z\)

Nous pouvons appliquer le processus de recherche d'une fonction potentielle à une force gravitationnelle. Rappelons que, si un objet a une masse unitaire et se trouve à l'origine, alors la force gravitationnelle exercée par l'objet sur un autre objet de masse unitaire au point\((x,y)\) est donnée par champ vectoriel.\(ℝ^2\)

\(\vecs F(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\),

où\(G\) est la constante gravitationnelle universelle. Dans l'exemple suivant, nous créons une fonction potentielle pour confirmer ce que nous savons déjà\(\vecs{F}\), à savoir que la gravité est conservatrice.

Exemple\(\PageIndex{7}\): Finding a Potential Function

Trouvez une fonction potentielle\(f\) pour\(\vecs{F}(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle\).

Solution

Supposons qu'il\(f\) s'agisse d'une fonction potentielle. Alors,\(\vecs \nabla f= \vecs{F}\) et donc

\[f_x(x,y)=\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }.\nonumber \]

Pour intégrer cette fonction par rapport à\(x\), nous pouvons utiliser\(u\) -substitution. Si\(u=x^2+y^2\), alors\(\dfrac{du}{2}=x\,dx\),

\[\begin{align*} \int \dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }\,dx &=\int \dfrac{−G}{2u^{3/2}} \,du \\[4pt] &=\dfrac{G}{\sqrt{u}}+h(y) \\[4pt] &=\dfrac{G}{\sqrt{x^2+y^2}}+h(y) \end{align*}\]

pour certaines fonctions\(h(y)\). Par conséquent,

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y).\nonumber \]

Comme\(f\) c'est une fonction potentielle pour\(\vecs{F}\),

\[f_y(x,y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }\nonumber \].

Depuis\(f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y)\), est\(f_y(x,y)\) également égal à\(\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)\).

Par conséquent,

\[\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }, \nonumber \]

ce qui implique que\(h′(y)=0\). Ainsi, nous pouvons prendre\(h(y)\) pour n'importe quelle constante ; en particulier, nous pouvons laisser\(h(y)=0\). La fonction

\[f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2} } \nonumber \]

est une fonction potentielle du champ gravitationnel\(\vecs{F}\). Pour confirmer qu'il\(f\) s'agit d'une fonction potentielle, notez que

\[\begin{align*} \vecs\nabla f(x,y) &=⟨−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} } (2x),−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} }(2y)⟩ \\[4pt] &=⟨\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }⟩\\[4pt] &=\vecs F(x,y). \end{align*}\]

Exercice\(\PageIndex{7}\)

Trouvez une fonction potentielle\(f\) pour la force gravitationnelle tridimensionnelle\(\vecs{F}(x,y,z)=\left\langle\dfrac{−Gx}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gz}{ {(x^2+y^2+z^2)}^{3/2} }\right\rangle\).

Allusion

Suivez la stratégie de résolution de problèmes.

Réponse

\(f(x,y,z)=\dfrac{G}{\sqrt{x^2+y^2+z^2}}\)

Tester un champ vectoriel

Jusqu'à présent, nous avons travaillé avec des champs vectoriels dont nous savons qu'ils sont conservateurs, mais si l'on ne nous dit pas qu'un champ vectoriel est conservateur, nous devons être en mesure de tester s'il est conservateur. Rappelez-vous que, s'il\(\vecs{F}\) est conservateur, il\(\vecs{F}\) possède alors la propriété partielle croisée (voir La propriété partielle croisée des champs vectoriels conservateurs). Autrement dit, si\(\vecs F=⟨P,Q,R⟩\) c'est conservateur\(P_y=Q_x\), alors\(P_z=R_x\), et\(Q_z=R_y\). Donc, s'il\(\vecs{F}\) a la propriété partielle croisée, est-ce\(\vecs{F}\) conservateur ? Si le domaine de\(\vecs{F}\) est ouvert et simplement connecté, la réponse est oui.

Théorème : LE TEST PARTIEL CROISÉ POUR LES CHAMPS CONSERVATEURS

\(\vecs{F}=⟨P,Q,R⟩\)Il s'agit d'un champ vectoriel sur une région ouverte et simplement connectée\(D\) et\(P_y=Q_x\)\(P_z=R_x\), et\(Q_z=R_y\) tout au long\(D\), il\(\vecs{F}\) est conservateur.

Bien que la preuve de ce théorème dépasse le cadre du texte, nous pouvons découvrir sa puissance à l'aide de quelques exemples. Plus tard, nous verrons pourquoi il est nécessaire que la région soit simplement connectée.

En combinant ce théorème à la propriété partielle croisée, nous pouvons déterminer si un champ vectoriel donné est conservateur :

Théorème : PROPRIÉTÉ PARTIELLE CROISÉE DES CHAMPS CONSERVATEURS

\(\vecs{F}=⟨P,Q,R⟩\)Soit un champ vectoriel sur une région ouverte et simplement connectée\(D\). Ensuite\(P_y=Q_x\)\(P_z=R_x\), et\(Q_z=R_y\) tout au long,\(D\) si et seulement si\(\vecs{F}\) c'est conservateur.

La version de ce théorème\(ℝ^2\) est également vraie. S'il s'\(\vecs F(x,y)=⟨P,Q⟩\)agit d'un champ vectoriel sur un domaine ouvert et simplement connecté dans\(ℝ^2\), alors\(\vecs F\) il est conservateur si et seulement si\(P_y=Q_x\).

Exemple\(\PageIndex{8}\): Determining Whether a Vector Field Is Conservative

Déterminez si le champ vectoriel\(\vecs F(x,y,z)=⟨xy^2z,x^2yz,z^2⟩\) est conservateur.

Solution

Notez que le domaine de\(\vecs{F}\) est entièrement\(ℝ^2\) et\(ℝ^3\) est simplement connecté. Par conséquent, nous pouvons utiliser la propriété croisée des champs vectoriels conservateurs pour déterminer si elle\(\vecs{F}\) est conservatrice. Laissez

\[P(x,y,z)=xy^2z \nonumber \]

\[Q(x,y,z)=x^2yz \nonumber \]

et

\[R(x,y,z)=z^2.\nonumber \]

Depuis\(Q_z(x,y,z)=x^2y\) et\(R_y(x,y,z)=0\), le champ vectoriel n'est pas conservateur.

Exemple\(\PageIndex{9}\): Determining Whether a Vector Field Is Conservative

Déterminez que le champ vectoriel\(\vecs{F}(x,y)=⟨x\ln (y), \,\dfrac{x^2}{2y}⟩\) est conservateur.

Solution

Notez que le domaine de\(\vecs{F}\) est la partie\(ℝ^2\) dans laquelle\(y>0\). Ainsi, le domaine de\(\vecs{F}\) fait partie d'un plan au-dessus de l'\(x\)axe -, et ce domaine est simplement connecté (il n'y a pas de trous dans cette région et cette région est connectée). Par conséquent, nous pouvons utiliser la propriété croisée des champs vectoriels conservateurs pour déterminer si elle\(\vecs{F}\) est conservatrice. Laissez

\[P(x,y)=x\ln (y) \;\; \text{and} \;\;\ Q(x,y)=\dfrac{x^2}{2y}. \nonumber \]

C'\(\vecs{F}\)est alors\(P_y(x,y)=\dfrac{x}{y}=Q_x(x,y)\) et donc conservateur.

Exercice\(\PageIndex{8}\)

Déterminez si\(\vecs{F}(x,y)=⟨\sin x\cos y,\,\cos x\sin y⟩\) c'est conservateur.

Allusion

Utilisez la propriété partielle croisée des champs vectoriels conservateurs de la section précédente.

Réponse

C'est conservateur.

Lorsque vous utilisez The Cross-Partial Property of Conservative Vector Fields, il est important de se rappeler qu'un théorème est un outil et, comme tout outil, il ne peut être appliqué que dans les bonnes conditions. Dans le cas de The Cross-Partial Property of Conservative Vector Fields, le théorème ne peut être appliqué que si le domaine du champ vectoriel est simplement connecté.

Pour voir ce qui peut mal tourner lors d'une mauvaise application du théorème, considérez le champ vectoriel de Example\(\PageIndex{4}\) :

\[\vecs F(x,y)=\dfrac{y}{x^2+y^2}\,\hat{\mathbf i}+\dfrac{−x}{x^2+y^2}\,\hat{\mathbf j}. \nonumber \]

Ce champ vectoriel satisfait à la propriété partielle croisée, puisque

\[\dfrac{∂}{∂y}\left(\dfrac{y}{x^2+y^2}\right)=\dfrac{(x^2+y^2)−y(2y)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2} \nonumber \]

et

\[\dfrac{∂}{∂x}\left(\dfrac{−x}{x^2+y^2}\right)=\dfrac{−(x^2+y^2)+x(2x)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2}. \nonumber \]

Puisque\(\vecs{F}\) satisfait à la propriété partielle croisée, nous pourrions être tentés de conclure que\(\vecs{F}\) c'est prudent. Cependant, n'\(\vecs{F}\)est pas conservateur. Pour voir cela, laissez

\[\vecs r(t)=⟨\cos t,\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

soit un paramétrage de la moitié supérieure d'un cercle unitaire orienté dans le sens antihoraire (indiquez-le\(C_1\)) et laissez

\[\vecs s(t)=⟨\cos t,−\sin t⟩,\;\; 0≤t≤\pi \nonumber \]

être un paramétrage de la moitié inférieure d'un cercle unitaire orienté dans le sens des aiguilles d'une montre (indiquez-le\(C_2\)). Remarquez cela\(C_1\) et\(C_2\) ayez le même point de départ et le même point d'arrivée. Depuis\({\sin}^2 t+{\cos}^2 t=1\),

\[\vecs F(\vecs r(t)) \cdot \vecs r′(t)=⟨\sin(t),−\cos(t)⟩ \cdot ⟨−\sin(t), \cos(t)⟩=−1 \nonumber \]

et

\[\vecs F(\vecs s(t))·\vecs s′(t)=⟨−\sin t,−\cos t⟩·⟨−\sin t,−\cos t⟩={\sin}^2 t+{\cos}^2t=1. \nonumber \]

Par conséquent,

\[\int_{C_1} \vecs F·d\vecs r=\int_0^{\pi}−1\,dt=−\pi \nonumber \]

et

\[\int_{C_2}\vecs F·d\vecs r=\int_0^{\pi} 1\,dt=\pi. \nonumber \]

Donc,\(C_1\) et\(C_2\) avoir le même point de départ et le même point d'arrivée, mais\(\int_{C_1} \vecs F·d\vecs r≠\int_{C_2} \vecs F·d\vecs r\). Par conséquent, n'\(\vecs{F}\)est pas indépendant du chemin et n'\(\vecs{F}\)est pas conservateur.

En résumé :\(\vecs{F}\) satisfait à la propriété partielle croisée tout en n'\(\vecs{F}\)étant pas conservateur. Qu'est-ce qui ne va pas ? Est-ce que cela contredit la propriété croisée des champs vectoriels conservateurs ? Le problème est que le domaine de\(\vecs{F}\) est entièrement,\(ℝ^2\) à l'exception de l'origine. En d'autres termes, le domaine de\(\vecs{F}\) possède un trou à l'origine et, par conséquent, le domaine n'est pas simplement connecté. Comme le domaine n'est pas simplement connecté, la propriété croisée des champs vectoriels conservateurs ne s'applique pas à\(\vecs{F}\).

Nous terminons cette section en examinant un exemple de l'utilité du théorème fondamental pour les intégrales linéaires. Maintenant que nous pouvons tester si un champ vectoriel est conservateur, nous pouvons toujours décider si le théorème fondamental des intégrales de lignes peut être utilisé pour calculer une intégrale de ligne vectorielle. Si l'on nous demande de calculer une intégrale de la forme\(\int_C \vecs F·d\vecs r\), notre première question devrait être la suivante : est-ce que c'est\(\vecs{F}\) conservateur ? Si la réponse est oui, alors nous devrions trouver une fonction potentielle et utiliser le théorème fondamental des intégrales linéaires pour calculer l'intégrale. Si la réponse est non, le théorème fondamental des intégrales linéaires ne peut pas nous aider et nous devons utiliser d'autres méthodes, comme utiliser la méthode de la section précédente (en utilisant\(\vecs F(\vecs r(t))\) et\(\vecs r'(t)\)).

Exemple\(\PageIndex{10}\): Using the Fundamental Theorem for Line Integrals

Calculez l'intégrale de la ligne\(\int_C \vecs F·d\vecs r\), où\(\vecs F(x,y,z)=⟨2xe^yz+e^xz,\,x^2e^yz,\,x^2e^y+e^x⟩\) et\(C\) est toute courbe lisse allant de l'origine à\((1,1,1)\).

Solution

Avant d'essayer de calculer l'intégrale, nous devons déterminer si elle\(\vecs{F}\) est conservatrice et si le domaine de\(\vecs{F}\) est simplement connecté. Le domaine de\(\vecs{F}\) est tout\(ℝ^3\), qui est connecté et ne comporte pas de trous. Par conséquent, le domaine de\(\vecs{F}\) est simplement connecté. Laissez

\[P(x,y,z)=2xe^yz+e^xz, \;\; Q(x,y,z)=x^2e^yz, \;\; \text{and} \;\; R(x,y,z)=x^2e^y+e^x \nonumber \]

pour que\(\vecs{F}(x,y,z)=⟨P,Q,R⟩\). Puisque le domaine de\(\vecs{F}\) est simplement connecté, nous pouvons vérifier les partiels croisés pour déterminer s'il\(\vecs{F}\) est conservateur. Notez que

\[\begin{align*} P_y(x,y,z) &=2xe^yz=Q_x(x,y,z) \\[4pt]P_z(x,y,z) &=2xe^y+e^x=R_x(x,y,z) \\[4pt] Q_z(x,y,z) &=x^2e^y=R_y(x,y,z).\end{align*}\]

Par conséquent,\(\vecs{F}\) est conservateur.

Pour évaluer\(\int_C \vecs F·d\vecs r\) l'utilisation du théorème fondamental pour les intégrales linéaires, nous devons trouver une fonction potentielle\(f\) pour\(\vecs{F}\). \(f\)Soyons une fonction potentielle pour\(\vecs{F}\). Alors\(\vecs \nabla f=\vecs F\), et donc\(f_x(x,y,z)=2xe^yz+e^xz\). Intégrer cette équation par rapport à\(x\) donne\(f(x,y,z)=x^2e^yz+e^xz+h(y,z)\) pour une certaine fonction\(h\). Différencier cette équation par rapport à\(y\) donne\(x^2e^yz+h_y(y,z)=Q(x,y,z)=x^2e^yz\), ce qui implique que\(h_y(y,z)=0\). Par conséquent,\(h\) est fonction\(z\) uniquement de, et\(f(x,y,z)=x^2e^yz+e^xz+h(z)\). Pour le trouver\(h\), notez que\(f_z=x^2e^y+e^x+h′(z)=R=x^2e^y+e^x\). Par conséquent,\(h′(z)=0\) et nous pouvons prendre\(h(z)=0\). Une fonction potentielle pour\(\vecs{F}\) est\(f(x,y,z)=x^2e^yz+e^xz\).

Maintenant que nous avons une fonction potentielle, nous pouvons utiliser le théorème fondamental des intégrales linéaires pour évaluer l'intégrale. Selon le théorème,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \vecs \nabla f·d\vecs r\\[4pt] &=f(1,1,1)−f(0,0,0)\\[4pt] &=2e. \end{align*}\]

Analyse

Notez que si nous n'avions pas reconnu que\(\vecs{F}\) c'est conservateur, nous aurions dû paramétrer\(C\) et utiliser la méthode de la section précédente. Comme la courbe\(C\) est inconnue, l'utilisation du théorème fondamental pour les intégrales linéaires est beaucoup plus simple.

Exercice\(\PageIndex{9}\)

Calculez l'intégrale\(\int_C \vecs F·d\vecs r\), où\(\vecs{F}(x,y)=⟨\sin x\sin y, 5−\cos x\cos y⟩\) et\(C\) est un demi-cercle avec point de départ\((0,\pi)\) et point final\((0,−\pi)\).

Allusion

Utilisez le théorème fondamental pour les intégrales linéaires.

Réponse

\(−10\pi\)

Exemple\(\PageIndex{11}\): Work Done on a Particle

\(\vecs F(x,y)=⟨2xy^2,2x^2y⟩\)Soyons un champ de force. Supposons qu'une particule commence son mouvement à l'origine et termine son mouvement à n'importe quel point d'un plan qui ne se trouve pas sur l'\(x\)axe ou l'\(y\)axe. De plus, le mouvement de la particule peut être modélisé à l'aide d'un paramétrage fluide. Montrez que\(\vecs{F}\) cela agit de manière positive sur la particule.

Solution

Nous montrons que\(\vecs{F}\) cela fonctionne de manière positive sur la particule en montrant qu'elle\(\vecs{F}\) est conservatrice, puis en utilisant le théorème fondamental pour les intégrales linéaires.

Pour montrer que\(\vecs{F}\) c'est conservateur, supposons que\(f(x,y)\) nous soyons une fonction potentielle pour\(\vecs{F}\). Ensuite,\(\vecs \nabla f(x,y)=\vecs F(x,y)=⟨2xy^2,2x^2y⟩\) et donc\(f_x(x,y)=2xy^2\) et\(f_y(x,y)=2x^2y\). L'équation\(fx(x,y)=2xy^2\) implique que\(f(x,y)=x^2y^2+h(y)\). Dériver les deux côtés en ce qui concerne\(y\) les rendements\(f_y(x,y)=2x^2y+h′(y)\). Par conséquent,\(h′(y)=0\) et nous pouvons prendre\(h(y)=0\).

Si\(f(x,y)=x^2y^2\), alors notez que\(\vecs \nabla f(x,y)=⟨2xy^2,2x^2y⟩=\vecs F\), et\(f\) c'est donc une fonction potentielle pour\(\vecs{F}\).

\((a,b)\)Soit le point où la particule arrête son mouvement, et\(C\) notons la courbe qui modélise le mouvement de la particule. Le travail effectué\(\vecs{F}\) sur la particule est\(\int_C \vecs{F}·d\vecs{r}\). Selon le théorème fondamental des intégrales linéaires,

\[\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \nabla f·d\vecs r \\[4pt] &=f(a,b)−f(0,0)\\[4pt] &=a^2b^2. \end{align*}\]

Depuis\(a≠0\) et\(b≠0\), par hypothèse,\(a^2b^2>0\). Par conséquent\(\int_C \vecs F·d\vecs r>0\), et\(\vecs{F}\) fait un travail positif sur la particule.

Analyse

Notez que ce problème serait beaucoup plus difficile sans utiliser le théorème fondamental pour les intégrales linéaires. Pour appliquer les outils que nous avons appris, il faudrait définir un paramétrage de la courbe et utiliser la méthode décrite dans la section précédente. Comme la trajectoire du mouvement\(C\) peut être aussi exotique que nous le souhaitons (tant qu'elle est lisse), il peut être très difficile de paramétrer le mouvement de la particule.

Exercice\(\PageIndex{10}\)

Supposons qu'une particule se déplace d'un point\((4,4)\) à un autre\((1,1)\) le long d'une courbe lisse.\(\vecs{F}(x,y)=⟨4x^3y^4,4x^4y^3⟩\) Le travail effectué\(\vecs{F}\) sur la particule est-il positif, négatif ou nul ?

Allusion

Utilisez le théorème fondamental pour les intégrales linéaires.

Réponse

NÉGATIF

Concepts clés

• Les théorèmes de cette section nécessitent des courbes fermées, simples ou les deux, et des régions connectées ou simplement connectées.
• L'intégrale linéaire d'un champ vectoriel conservateur peut être calculée à l'aide du théorème fondamental des intégrales linéaires. Ce théorème est une généralisation du théorème fondamental du calcul dans les dimensions supérieures. L'utilisation de ce théorème facilite généralement le calcul de l'intégrale linéaire.
• Les champs conservateurs sont indépendants du chemin. L'intégrale linéaire d'un champ conservateur dépend uniquement de la valeur de la fonction potentielle aux extrémités de la courbe du domaine.
• Un champ vectoriel donné\(\vecs{F}\), nous pouvons vérifier s'il\(\vecs{F}\) est conservateur en utilisant la propriété cross-partial. S'il\(\vecs{F}\) possède la propriété de partialité croisée et que le domaine est simplement connecté, il\(\vecs{F}\) est conservateur (et a donc une fonction potentielle). Si elle\(\vecs{F}\) est prudente, nous pouvons trouver une fonction potentielle en utilisant la stratégie de résolution de problèmes.
• La circulation d'un champ vectoriel conservateur sur un domaine simplement connecté sur une courbe fermée est nulle.

Équations clés

• Théorème fondamental des intégrales linéaires
  \(\displaystyle \int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)
• Circulation d'un champ conservateur sur la courbe C qui entoure une région simplement connectée
  \(\displaystyle \oint_C \vecs \nabla f·d\vecs r=0\)

Lexique

courbe fermée

une courbe qui commence et se termine au même point

région connectée

une région dans laquelle deux points quelconques peuvent être connectés par un chemin avec une trace entièrement contenue dans la région

Théorème fondamental pour les intégrales linéaires

la valeur de l'intégrale linéaire\(\displaystyle \int_C\vecs ∇f⋅d\vecs r\) dépend uniquement de la valeur de aux\(f\) extrémités de\(C: \displaystyle \int_C \vecs ∇f⋅d\vecs r=f(\vecs r(b))−f(\vecs r(a))\)

indépendance du chemin

un champ vectoriel\(\vecs{F}\) est indépendant de la trajectoire, s'il s'\(\displaystyle \int_{C_1} \vecs F⋅d\vecs r=\displaystyle \int_{C_2} \vecs F⋅d\vecs r\)agit de courbes\(C_1\) et\(C_2\) dans le domaine de\(\vecs{F}\) ayant les mêmes points initiaux et terminaux

courbe simple

une courbe qui ne se croise pas

région simplement connectée

une région qui est connectée et dont la propriété est que toute courbe fermée située entièrement à l'intérieur de la région englobe des points qui se trouvent entièrement à l'intérieur de la région