Skip to main content
Global

16.2E : Exercices pour la section 16.2

  1. Last updated
  2. Save as PDF
  • Page ID
    197901

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Vrai ou faux ? \(\displaystyle\int _C f(x,y)\,ds\)L'intégrale linéaire est égale à une intégrale définie s'il s'\(C\)agit d'une courbe lisse définie sur\([a,b]\) et si la fonction\(f\) est continue sur une région contenant une courbe\(C\).

    Réponse
    Vrai

    2. Vrai ou faux ? Les fonctions vectorielles\(\vecs r_1=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}, \quad 0≤t≤1,\)\(\vecs r_2=(1−t)\,\hat{\mathbf i}+(1−t)^2\,\hat{\mathbf j}, \quad 0≤t≤1\) et définissent la même courbe orientée.

    3. Vrai ou faux ? \(\displaystyle\int _{−C}(P\,dx+Q\,dy)=\int _C(P\,dx−Q\,dy)\)

    Réponse
    Faux

    4. Vrai ou faux ? Une courbe lisse par morceaux\(C\) est constituée d'un nombre fini de courbes lisses qui sont jointes bout à bout.

    5. Vrai ou faux ? Si\(C\) est donné par\(x(t)=t,\quad y(t)=t, \quad 0≤t≤1\), alors\(\displaystyle\int _Cxy\,ds=\int ^1_0t^2\,dt.\)

    Réponse
    Faux

    Pour les exercices suivants, utilisez un système d'algèbre informatique (CAS) pour évaluer les intégrales linéaires sur le chemin indiqué.

    6. [T]\(\displaystyle\int _C(x+y)\,ds\)

    \(C:x=t,y=(1−t),z=0\)du\((0, 1, 0)\) au\((1, 0, 0)\)

    7. [T]\(\displaystyle \int _C(x−y)ds\)

    \(C:\vecs r(t)=4t\,\hat{\mathbf i}+3t\,\hat{\mathbf j}\)quand\(0≤t≤2\)

    Réponse
    \(\displaystyle\int _C(x−y)\,ds=10\)

    8. [T]\(\displaystyle\int _C(x^2+y^2+z^2)\,ds\)

    \(C:\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j}+8t\,\hat{\mathbf k}\)quand\(0≤t≤\dfrac{π}{2}\)

    9. [T] Évaluez\(\displaystyle\int _Cxy^4\,ds\), où se\(C\) trouve la moitié droite du cercle\(x^2+y^2=16\) et où elle est parcourue dans le sens des aiguilles d'une montre.

    Réponse
    \(\displaystyle\int _Cxy^4\,ds=\frac{8192}{5}\)

    10. [T] Évaluez\(\displaystyle\int _C4x^3ds\), où C est le segment de droite allant de\((−2,−1)\) à\((1, 2)\).

    Pour les exercices suivants, trouvez le travail effectué.

    11. Trouvez le travail effectué par champ vectoriel\(\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}\) sur une particule se déplaçant le long d'un segment de droite allant de\((1,4,2)\) à\((0,5,1)\).

    Réponse
    \(W=8\)unités de travail

    12. Trouvez le travail effectué par une personne pesant 150 livres qui marche exactement un tour sur un escalier circulaire en colimaçon d'un rayon de 3 pieds si la personne se lève de 10 pieds.

    13. Trouvez le travail effectué par champ de force\(\vecs F(x,y,z)=−\dfrac{1}{2}x\,\hat{\mathbf i}−\dfrac{1}{2}y\,\hat{\mathbf j}+\dfrac{1}{4}\,\hat{\mathbf k}\) sur une particule lorsqu'elle se déplace le long de l'hélice\(\vecs r(t)=\cos t\,\hat{\mathbf i}+\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k}\) d'un point\((1,0,0)\) à l'autre\((−1,0,3π)\).

    Réponse
    \(W=\frac{3π}{4}\)unités de travail

    14. Trouvez le travail effectué par champ vectoriel\(\vecs{F}(x,y)=y\,\hat{\mathbf i}+2x\,\hat{\mathbf j}\) en déplaçant un objet le long d'une trajectoire\(C\), qui joint des points\((1, 0)\) et\((0, 1)\).

    15. Trouvez le travail effectué par la force\(\vecs{F}(x,y)=2y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}+(x+y)\,\hat{\mathbf k}\) en déplaçant un objet le long d'une courbe\(\vecs r(t)=\cos(t)\,\hat{\mathbf i}+\sin(t)\,\hat{\mathbf j}+16\,\hat{\mathbf k}\), où\(0≤t≤2π\).

    Réponse
    \(W=π\)unités de travail

    16. Détermine la masse d'un fil en forme de cercle de rayon 2 centré en (3, 4) avec une densité de masse linéaire\(ρ(x,y)=y^2\).

    Pour les exercices suivants, évaluez les intégrales linéaires.

    17. Évaluez\(\displaystyle\int_C\vecs F·d\vecs{r}\)\(\vecs{F}(x,y)=−1\,\hat{\mathbf j}\), où et\(C\) est la partie du graphique\(y=\frac{1}{2}x^3−x\) allant de\((2,2)\) à\((−2,−2)\).

    Réponse
    \(\displaystyle\int _C\vecs F·d\vecs{r}=4\)unités de travail

    18. Évaluez\(\displaystyle\int _γ(x^2+y^2+z^2)^{−1}ds\), où\(γ\) se trouve l'hélice\(x=\cos t,y=\sin t,z=t,\) avec\(0≤t≤T.\)

    19. Évaluez\(\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz\) sur le segment de ligne de\((1,1,1) \) à\((3,2,0).\)

    Réponse
    \(\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz=−1\)

    20. \(C\)Soit le segment de ligne du point (0, 1, 1) au point (2, 2, 3). Evaluer l'intégrale\(\displaystyle\int _Cy\,ds.\)

    21. [T] Utilisez un système d'algèbre informatique pour évaluer l'intégrale de la droite\(\displaystyle\int _Cy^2\,dx+x\,dy\), où\(C\) est l'arc de la parabole\(x=4−y^2\) de\((−5, −3)\) à\((0, 2)\).

    Réponse
    \(\displaystyle\int _C(y^2)\,dx+(x)\,dy=\dfrac{245}{6}\)

    22. [T] Utilisez un système d'algèbre informatique pour évaluer l'intégrale de la droite\(\displaystyle\int _C (x+3y^2)\,dy\) sur la trajectoire\(C\) donnée par\(x=2t,y=10t,\) où\(0≤t≤1.\)

    23. [T] Utilisez un CAS pour évaluer l'intégrale de la ligne\(\displaystyle\int _C xy\,dx+y\,dy\) sur la trajectoire\(C\) donnée par\(x=2t,y=10t\), où\(0≤t≤1\).

    Réponse
    \(\displaystyle\int _Cxy\,dx+y\,dy=\dfrac{190}{3}\)

    24. Évaluez l'intégrale de la ligne\(\displaystyle\int _C(2x−y)\,dx+(x+3y)\,dy\),\(C\) qui se trouve le long de\(x\) l'axe -de\(x=0\) à\(x=5\).

    26. [T] Utilisez un CAS pour évaluer\(\displaystyle\int _C\dfrac{y}{2x^2−y^2}\,ds\), où cela\(C\) est défini par les équations paramétriques\(x=t,y=t\), pour\(1≤t≤5.\)

    Réponse
    \(\displaystyle\int _C\frac{y}{2x^2−y^2}\,ds=\sqrt{2}\ln 5\)

    27. [T] Utilisez un CAS pour évaluer\(\displaystyle\int _Cxy\,ds\), où cela\(C\) est défini par les équations paramétriques\(x=t^2,y=4t\), pour\(0≤t≤1.\)

    Dans les exercices suivants, trouvez le travail effectué par champ de force\(\vecs F\) sur un objet se déplaçant le long de la trajectoire indiquée.

    28. \(\vecs{F}(x,y)=−x \,\hat{\mathbf i}−2y\,\hat{\mathbf j}\)

    \(C:y=x^3\)du\((0, 0)\) au\((2, 8)\)

    Réponse
    \(W=−66\)unités de travail

    29. \(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)

    <\(C\) : dans le sens antihoraire autour du triangle avec des sommets\((0, 0), (1, 0), \) et\((1, 1)\)

    30. \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}−5z\,\hat{\mathbf k}\)

    \(C:\vecs r(t)=2\cos t\,\hat{\mathbf i}+2\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k},\; 0≤t≤2π\)

    Réponse
    \(W=−10π^2\)unités de travail

    31. \(\vecs F\)Soit un champ vectoriel\(\vecs{F}(x,y)=(y^2+2xe^y+1)\,\hat{\mathbf i}+(2xy+x^2e^y+2y)\,\hat{\mathbf j}\). Calculez le travail de l'intégrale\(\displaystyle\int _C\vecs F·d\vecs{r}\), où\(C\) est le chemin\(\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j},\quad 0≤t≤\dfrac{π}{2}\).

    32. Calculez le travail effectué par la force\(\vecs F(x,y,z)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}−z\,\hat{\mathbf k}\) le long du chemin\(\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+t^3\,\hat{\mathbf k}\), où\(0≤t≤1\).

    Réponse
    \(W=2\)unités de travail

    33. Évaluez\(\displaystyle\int _C\vecs F·d\vecs{r}\), où\(\vecs{F}(x,y)=\dfrac{1}{x+y}\,\hat{\mathbf i}+\dfrac{1}{x+y}\,\hat{\mathbf j}\) et\(C\) est le segment du cercle unitaire allant dans le sens antihoraire de\((1,0)\) à\((0, 1)\).

    34. La force\(\vecs F(x,y,z)=zy\,\hat{\mathbf i}+x\,\hat{\mathbf j}+z^2x\,\hat{\mathbf k}\) agit sur une particule qui se déplace de l'origine au point\((1, 2, 3)\). Calculez le travail effectué si la particule se déplace :

    1. le long de la trajectoire\((0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)\) le long de segments rectilignes joignant chaque paire de points d'extrémité ;
    2. le long de la ligne droite joignant les points initial et final.
    3. Le travail est-il le même sur les deux voies ?

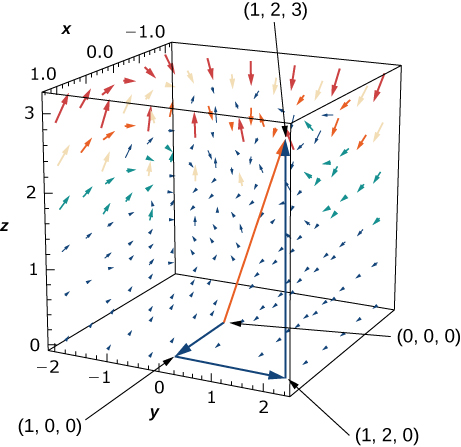
      clipboard_e7c787ff46860b19ec57c0669a08914af.png

    Réponse
    a.\(W=11\) unités de travail ;
    b.\(W=\dfrac{39}{4}=9\frac{3}{4}\) unités de travail ;
    c. Non

    35. Trouvez le travail effectué par champ vectoriel\(\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}\) sur une particule se déplaçant le long d'un segment de droite allant de\((1, 4, 2)\) à\((0, 5, 1).\)

    36. Combien de travail est nécessaire pour déplacer un objet dans un champ vectoriel\(\vecs{F}(x,y)=y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}\) le long de la partie supérieure de l'ellipse\(\dfrac{x^2}{4}+y^2=1\) de\((2, 0)\) à\((−2,0)\) ?

    Réponse
    \(W=2π\)unités de travail

    37. Un champ vectoriel est donné par\(\vecs{F}(x,y)=(2x+3y)\,\hat{\mathbf i}+(3x+2y)\,\hat{\mathbf j}\). Évaluez l'intégrale linéaire du champ autour d'un cercle de rayon unitaire parcouru dans le sens des aiguilles d'une montre.

    38. Évaluez l'intégrale linéaire de la fonction scalaire\(xy\) le long du chemin parabolique\(y=x^2\) reliant l'origine au point\((1, 1)\).

    Réponse
    \(\displaystyle\int _C f\,ds=\dfrac{25\sqrt{5}+1}{120}\)

    39. Trouvez\(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy\)\(C: y=3x\) du\((0, 0)\) au\((1, 3).\)

    40. Trouvez\(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy\)\(C: y^2=9x\) du\((0, 0)\) au\((1, 3).\)

    Réponse
    \(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy=6.15\)

    Pour les exercices suivants, utilisez un CAS pour évaluer les intégrales de ligne données.

    41. [T] Évaluer\(\vecs F(x,y,z)=x^2z\,\hat{\mathbf i}+6y\,\hat{\mathbf j}+yz^2\,\hat{\mathbf k}\), où\(C\) est représenté par\(\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+\ln t \,\hat{\mathbf k},1≤t≤3\).

    42. [T] Évaluez l'intégrale de la ligne\(\displaystyle\int _γxe^y\,ds\) où,\(γ\) est l'arc de la courbe\(x=e^y\) de\((1,0)\) à\((e,1)\).

    Réponse
    \(\displaystyle\int _γxe^y\,ds≈7.157\)

    43. [T] Évaluez l'intégrale\(\displaystyle\int _γxy^2\,ds\), où\(γ\) est un triangle avec des sommets\((0, 1, 2), (1, 0, 3)\), et\((0,−1,0)\).

    44. [T] Évaluez l'intégrale de la ligne\(\displaystyle\int _γ(y^2−xy)\,dx\), où\(γ\) est la courbe\(y=\ln x\) de\((1, 0)\) vers\((e,1)\).

    Réponse
    \(\displaystyle\int _γ(y^2−xy)\,dx≈−1.379\)

    45. [T] Évaluez l'intégrale de la ligne\(\displaystyle\int_γ xy^4\,ds\), où\(γ\) se trouve la moitié droite du cercle\(x^2+y^2=16\).

    46. [T] Évaluez\(\int C \vecs F⋅d\vecs{r},\int C \vecs F·d\vecs{r},\) où\(\vecs F(x,y,z)=x^2y\,\mathbf{\hat i}+(x−z)\,\mathbf{\hat j}+xyz\,\mathbf{\hat k}\) et

    \(C: \vecs r(t)=t\,\mathbf{\hat i}+t^2\,\mathbf{\hat j}+2\,\mathbf{\hat k},0≤t≤1\).

    Réponse
    \(\displaystyle\int _C \vecs F⋅d\vecs{r}≈−1.133\)unités de travail

    47. Évaluez\(\displaystyle\int _C \vecs F⋅d\vecs{r}\), où\(\vecs{F}(x,y)=2x\sin y\,\mathbf{\hat i}+(x^2\cos y−3y^2)\,\mathbf{\hat j}\) et

    \(C\)est n'importe quel chemin allant de\((−1,0)\) à\((5, 1)\).

    48. Détermine l'intégrale linéaire de\(\vecs F(x,y,z)=12x^2\,\mathbf{\hat i}−5xy\,\mathbf{\hat j}+xz\,\mathbf{\hat k}\) la trajectoire\(C\) définie par un\(y=x^2, z=x^3\) point\((0, 0, 0)\) à l'autre\((2, 4, 8)\).

    Réponse
    \(\displaystyle\int _C \vecs F⋅d\vecs{r}≈22.857\)unités de travail

    49. Trouve l'intégrale de la droite de\(\displaystyle\int _C(1+x^2y)\,ds\), d'où\(C\)\(\vecs r(t)=2\cos t\,\mathbf{\hat i}+3\sin t\,\mathbf{\hat j}\) vient l'ellipse\(0≤t≤π.\)

    Pour les exercices suivants, trouvez le flux.

    50. Calculez le flux de part et d'\(\vecs{F}=x^2\,\mathbf{\hat i}+y\,\mathbf{\hat j}\)autre d'un segment\((0, 0)\) de ligne\((1, 2).\)

    Réponse
    \(\text{flux}=−\frac{1}{3}\)

    51. Laissez\(\vecs{F}=5\,\mathbf{\hat i}\) et\(C\) laissez-vous courber\(y=0,\) avec\(0≤x≤4\). Trouvez le flux à travers\(C\).

    52. Laissez\(\vecs{F}=5\,\mathbf{\hat j}\) et\(C\) laissez-vous courber\(y=0,\) avec\(0≤x≤4\). Trouvez le flux à travers\(C\).

    Réponse
    \(\text{flux}=-20\)

    53. Laisse\(\vecs{F}=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}\) et laisse\(C: \vecs r(t)=\cos t\,\mathbf{\hat i}+\sin t\,\mathbf{\hat j}\)\(0≤t≤2π\). Calculez le flux traversant\(C\).

    54. Laissez\(\vecs{F}=(x^2+y^3)\,\mathbf{\hat i}+(2xy)\,\mathbf{\hat j}\). Calculez le flux\(\vecs F\) orienté dans le sens antihoraire sur la courbe\(C: x^2+y^2=9.\)

    Réponse
    \(\text{flux}=0\)

    Terminez le reste des exercices comme indiqué.

    55. Trouvez l'intégrale de la ligne\(\displaystyle\int _C z^2\,dx+y\,dy+2y\,dz,\) où\(C\) se compose de deux parties :\(C_1\) et\(C_2.\)\(C_1\) est l'intersection du cylindre\(x^2+y^2=16\) et du plan\(z=3\) de\((0, 4, 3)\) à\((−4,0,3).\)\(C_2\) est un segment de droite de\((−4,0,3)\) à\((0, 1, 5)\).

    56. Un ressort est constitué d'un fil fin tordu en forme d'hélice circulaire.\(x=2\cos t,\;y=2\sin t,\;z=t.\) Trouvez la masse de deux tours du ressort si le fil a une densité de masse constante de\(ρ\) grammes par cm.

    Réponse
    \(m=4πρ\sqrt{5}\)grammes

    57. Un fil fin est plié en forme de demi-cercle de rayon\(a\). Si la densité de masse linéaire au point\(P\) est directement proportionnelle à sa distance par rapport à la ligne passant par les extrémités, déterminez la masse du fil.

    58. Un objet se déplace dans le champ de force dans le\(\vecs F(x,y,z)=y^2\,\mathbf{\hat i}+2(x+1)y\,\mathbf{\hat j}\) sens antihoraire à partir d'un point situé\((2, 0)\) le long\(x^2+4y^2=4\) d'une trajectoire elliptique jusqu'à un point situé\((2, 0)\) le long de l'\(x\)axe\((−2,0)\), puis Quel est le travail effectué par le champ de force sur l'objet ?

    Réponse
    \(W=0\)unités de travail

    59. Trouvez le travail effectué lorsqu'un objet se déplace dans\(\vecs F(x,y,z)=2x\,\mathbf{\hat i}−(x+z)\,\mathbf{\hat j}+(y−x)\,\mathbf{\hat k}\) le champ de force le long de la trajectoire donnée par\(\vecs r(t)=t^2\,\mathbf{\hat i}+(t^2−t)\,\mathbf{\hat j}+3\,\mathbf{\hat k}, \; 0≤t≤1.\)

    60. Si un champ de force inverse\(\vecs F\) est donné par\(\vecs F(x,y,z)=\dfrac{k}{‖r‖^3}r\), où\(k\) est une constante, trouvez le travail effectué par\(\vecs F\) lorsque son point d'application se déplace le long de l'\(x\)axe -de\(A(1,0,0)\) à\(B(2,0,0)\).

    Réponse
    \(W=\frac{k}{2}\)unités de travail

    61. David et Sandra prévoient d'évaluer l'intégrale de la ligne\(\displaystyle\int _C\vecs F·d\vecs{r}\) le long d'une trajectoire dans le\(xy\) plan -allant de\((0, 0)\) à\((1, 1)\). Le champ de force est\(\vecs{F}(x,y)=(x+2y)\,\mathbf{\hat i}+(−x+y^2)\,\mathbf{\hat j}\). David choisit la trajectoire qui suit l'\(x\)axe -de\((0, 0)\) à,\((1, 0)\) puis suit la ligne verticale\((1, 0)\) jusqu'au\(x=1\) point final\((1, 1)\). Sandra choisit le chemin direct le long de la diagonale\(y=x\) allant de\((0, 0)\) à\((1, 1)\). Quelle intégrale de ligne est la plus grande et de combien ?