16.2 : Intégrales de ligne
- Page ID
- 197892
Intro
- Calculez une intégrale scalaire le long d'une courbe.
- Calculez une intégrale de ligne vectorielle le long d'une courbe orientée dans l'espace.
- Utilisez une intégrale linéaire pour calculer le travail effectué pour déplacer un objet le long d'une courbe dans un champ vectoriel.
- Décrivez le flux et la circulation d'un champ vectoriel.
Nous connaissons les intégrales à variable unique de la forme\(\displaystyle \int_{a}^{b}f(x)\,dx\), où le domaine d'intégration est un intervalle\([a,b]\). Un tel intervalle peut être considéré comme une courbe dans le\(xy\) plan, car l'intervalle définit un segment de droite avec des extrémités\((a,0)\) et,\((b,0)\) en d'autres termes, un segment de droite situé sur l'\(x\)axe. Supposons que nous souhaitions effectuer une intégration sur n'importe quelle courbe du plan, et pas uniquement sur un segment de ligne sur l'\(x\)axe. Une telle tâche nécessite un nouveau type d'intégrale, appelée intégrale linéaire.
Les intégrales linéaires ont de nombreuses applications en ingénierie et en physique. Ils nous permettent également de faire plusieurs généralisations utiles du théorème fondamental du calcul. De plus, ils sont étroitement liés aux propriétés des champs vectoriels, comme nous le verrons.
Intégrales de lignes scalaires
Une intégrale linéaire nous permet d'intégrer des fonctions multivariables et des champs vectoriels sur des courbes arbitraires dans un plan ou dans l'espace. Il existe deux types d'intégrales linéaires : les intégrales linéaires scalaires et les intégrales linéaires vectorielles. Les intégrales de lignes scalaires sont des intégrales d'une fonction scalaire sur une courbe dans un plan ou dans l'espace. Les intégrales de lignes vectorielles sont des intégrales d'un champ vectoriel au-dessus d'une courbe dans un plan ou dans l'espace. Examinons d'abord les intégrales des lignes scalaires.
Une intégrale scalaire est définie de la même manière qu'une intégrale à variable unique, sauf que pour une intégrale scalaire, l'integrand est fonction de plusieurs variables et que le domaine d'intégration est une courbe dans un plan ou dans l'espace, par opposition à une courbe sur l'\(x\)axe.
Pour une intégrale scalaire, on utilise une courbe lisse dans un plan ou dans l'espace et on laisse ff être une fonction dont le domaine inclut\(C\).\(C\) Nous coupons la courbe en petits morceaux. Pour chaque pièce, nous choisissons un point\(P\) dans cette pièce et évaluons\(f\) à\(P\). (Nous pouvons le faire car tous les points de la courbe se situent dans le domaine de\(f\).) Nous multiplions\(f(P)\) par la longueur de l'arc de la pièce\(\Delta s\), ajoutons le produit\(f(P)\Delta s\) sur toutes les pièces, puis laissons la longueur de l'arc des pièces diminuer à zéro en prenant une limite. Le résultat est l'intégrale scalaire de la fonction au-dessus de la courbe.
Pour une description formelle d'une intégrale scalaire, prenons\(C\) une courbe lisse dans l'espace donnée par la paramétrisation\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). \(f(x,y,z)\)Soit une fonction dont le domaine inclut la courbe\(C\). Pour définir l'intégrale droite de la fonction\(f\) terminée\(C\), nous commençons comme la plupart des définitions d'une intégrale commencent : nous découpons la courbe en petits morceaux. Divisez l'intervalle des paramètres\([a,b]\) en\(n\) sous-intervalles\([t_{i−l},t_i]\) de même largeur pour\(1≤i≤n\), où\(t_0=a\) et\(t_n=b\) (Figure\(\PageIndex{1}\)). \(t_{i}^*\)Soit une valeur dans l'\(i^{th}\)intervalle\([t_{i−l},t_i]\). Désignez les points de terminaison de\(\vecs r(t_0)\)\(\vecs r(t_1)\),,...,\(\vecs r(t_n)\) par\(P_0\),...,\(P_n\). Les points P i divisent la courbe\(C\) en\(n\) morceaux\(C_1\)\(C_2\),,...\(C_n\),, avec des longueurs\(\Delta s_1\)\(\Delta s_2\),,...\(\Delta s_n\), respectivement. \(P_{i}^*\)Dénotons le point final de\(\vecs r(t_{i}^*)\) for\(1≤i≤n\). Maintenant, nous évaluons la fonction\(f\) au point\(P_{i}^*\) pour\(1≤i≤n\). Notez que\(P_{i}^*\) c'est en pièce\(C_1\) et qu'\(P_{i}^*\)il appartient donc au domaine de\(f\). Multipliez\(f(P_{i}^*)\) par la longueur\(\Delta s_1\) de\(C_1\), ce qui donne la surface de la « feuille » avec la base\(C_1\) et la hauteur\(f(P_{i}^{*})\). Ceci est similaire à l'utilisation de rectangles pour approximer la surface dans une intégrale à variable unique. Maintenant, nous formons la somme\(\displaystyle \sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i\).
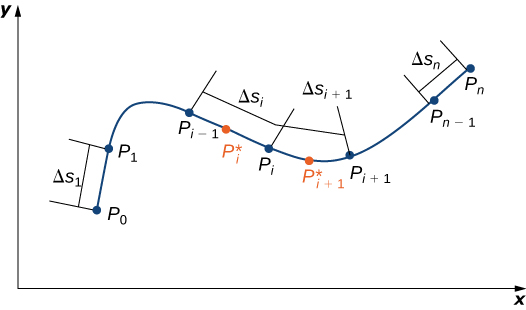
Notez la similitude de cette somme par rapport à une somme de Riemann ; en fait, cette définition est une généralisation d'une somme de Riemann à des courbes arbitraires dans l'espace. Tout comme pour les sommes et les intégrales de forme de Riemann\(\displaystyle \int_{a}^{b}g(x)\,dx\), nous définissons une intégrale en laissant la largeur des parties de la courbe se réduire à zéro en prenant une limite. Le résultat est l'intégrale scalaire de\(f\) along\(C\).
Vous avez peut-être remarqué une différence entre cette définition d'une intégrale linéaire scalaire et d'une intégrale à variable unique. Dans cette définition, les longueurs d'arc\(\Delta s_1\)\(\Delta s_2\),...,\(\Delta s_n\) ne sont pas nécessairement les mêmes ; dans la définition d'une intégrale à variable unique, la courbe de l'\(x\)axe -est divisée en morceaux de même longueur. Cette différence n'a aucun effet sur la limite. Lorsque nous réduisons les longueurs des arcs à zéro, leurs valeurs deviennent suffisamment proches pour que toute petite différence ne soit plus pertinente.
\(f\)Soit une fonction dont le domaine inclut la courbe\(C\) lisse paramétrée par\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). L'intégrale scalaire de\(f\) along\(C\) est
\[\int_C f(x,y,z) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n}f(P_{i}^{*})\,\Delta s_i \label{eq12a} \]
si cette limite existe (\(t_i ^{*}\)et\(\Delta s_i\) est définie comme dans les paragraphes précédents). S'il s'\(C\)agit d'une courbe plane, elle\(C\) peut alors être représentée par les équations paramétriques\(x=x(t)\)\(y=y(t)\), et\(a≤t≤b\). Si\(C\) est lisse et\(f(x,y)\) dépend de deux variables, alors l'intégrale scalaire de\(f\) along\(C\) est définie de la même manière que
\[\int_C f(x,y) \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} f(P_{i}^{*})\,\Delta s_i, \label{eq13} \]
si cette limite existe.
S'il s'\(f\)agit d'une fonction continue sur une courbe lisse\(C\), elle existe\(\displaystyle \int_C f \,ds\) toujours. Comme elle\(\displaystyle \int_C f \,ds\) est définie comme une limite des sommes de Riemann, la continuité de\(f\) est suffisante pour garantir l'existence de la limite, tout comme l'intégrale\(\displaystyle \int_{a}^{b}g(x)\,dx\) existe si elle\(g\) est continue\([a,b]\).
Avant d'examiner comment calculer une intégrale linéaire, nous devons examiner la géométrie capturée par ces intégrales. Supposons que\(f(x,y)≥0\) pour tous\((x,y)\) les points d'une courbe plane lisse\(C\). Imaginez que vous prenez une courbe\(C\) et que vous la projetez « vers le haut » jusqu'à la surface définie par\(f(x,y)\), créant ainsi une nouvelle courbe\(C′\) qui se trouve dans le graphique de\(f(x,y)\) (Figure\(\PageIndex{2}\)). Nous déposons maintenant une « feuille » du\(C′\) bas vers le\(xy\) plan. La superficie de cette feuille est\(\displaystyle \int_C f(x,y)ds\). Si\(f(x,y)≤0\) pour certains points\(C\), la valeur de\(\displaystyle \int_C f(x,y)\,ds\) est la surface au-dessus du\(xy\) plan -moins la zone située sous le\(xy\) plan. (Notez la similitude avec les intégrales du formulaire\(\displaystyle \int_{a}^{b}g(x)\,dx\).)
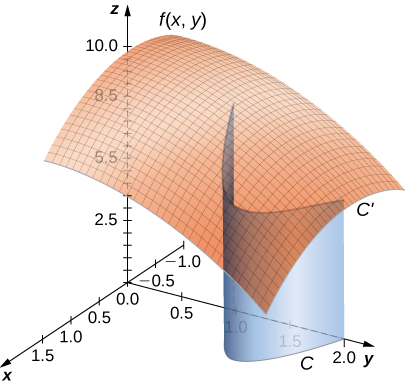
À partir de cette géométrie, nous pouvons voir que l'intégrale de la ligne\(\displaystyle \int_C f(x,y)\,ds\) ne dépend pas du paramétrage\(\vecs r(t)\) de\(C\). Tant que la courbe est parcourue exactement une fois par le paramétrage, la surface de la feuille formée par la fonction et la courbe est la même. Ce même type d'argument géométrique peut être étendu pour montrer que l'intégrale linéaire d'une fonction à trois variables sur une courbe dans l'espace ne dépend pas du paramétrage de la courbe.
Détermine la valeur de l'intégrale\(\displaystyle \int_C 2\,ds\), où\(C\) est la moitié supérieure du cercle unitaire.
Solution
L'integrand est\(f(x,y)=2\). La figure\(\PageIndex{3}\) montre le graphique\(f(x,y)=2\) de la courbe C et la feuille formée par celles-ci. Notez que cette feuille a la même surface qu'un rectangle en largeur\(\pi\) et en longueur\(2\). Par conséquent,\(\displaystyle \int_C 2 \,ds=2\pi\,\text{units}^2\).
Pour voir cela\(\displaystyle \int_C 2 \,ds=2\pi\) en utilisant la définition de l'intégrale de ligne,\(\vecs r(t)\) nous utilisons un paramétrage de\(C\). Ensuite,\(f(\vecs r(t_i))=2\) pour n'importe\(t_i\) quel numéro du domaine de\(\vecs r\). Par conséquent,
\[\begin{align*} \int_C f \,ds &=\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_{i}^{*}))\,\Delta s_i \\[4pt] &=\lim_{n\to\infty}\sum_{i=1}^{n}2\,\Delta s_i \\[4pt] &=2\lim_{n\to\infty}\sum_{i=1}^{n}\,\Delta s_i \\[4pt] &=2(\text{length}\space \text{of}\space C) \\[4pt] &=2\pi \,\text{units}^2. \end{align*}\]
Trouvez la valeur de\(\displaystyle \int_C(x+y)\,ds\), où se\(C\) trouve la courbe paramétrée par\(x=t\),\(y=t\),\(0≤t≤1\).
- Allusion
-
Trouvez la forme formée par\(C\) et le graphe de la fonction\(f(x,y)=x+y\).
- Réponse
-
\(\sqrt{2}\)
Notez que dans une intégrale scalaire, l'intégration se fait par rapport à la longueur de l'arc\(s\), ce qui peut rendre difficile le calcul d'une intégrale scalaire. Pour faciliter les calculs, nous pouvons\(\displaystyle \int_C f\,ds\) traduire par une intégrale avec une variable d'intégration, c'est-à-dire\(t\).
\(a≤t≤b\)Soit\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\) un paramétrage de\(C\). Puisque nous supposons que\(C\) c'est fluide,\(\vecs r′(t)=⟨x′(t),y′(t),z′(t)⟩\) c'est continu pour tous\(t\)\([a,b]\). En particulier\(x′(t)\),\(y′(t)\), et\(z′(t)\) existent pour tous\(t\)\([a,b]\). Selon la formule de la longueur de l'arc, nous avons
\[\text{length}(C_i)=\Delta s_i=\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt. \nonumber \]
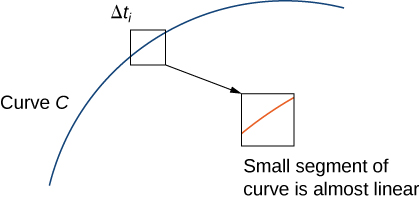
Si la largeur\(\Delta t_i=t_i−t_{i−1}\) est petite\(\displaystyle \int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_i^*)‖\,\Delta t_i\), la fonction\(‖\vecs r′(t)‖\) est presque constante sur l'intervalle\([t_{i−1},t_i]\). Par conséquent,
\[\int_{t_{i−1}}^{t_i} ‖\vecs r′(t)‖\,dt\,≈\,‖\vecs r′(t_{i}^{*})‖\,\Delta t_i, \label{approxLineIntEq1} \]
et nous avons
\[\sum_{i=1}^{n} f(\vecs r(t_i^*))\,\Delta s_i\approx\sum_{i=1}^{n} f(\vecs r(t_{i}^{*})) ‖\vecs r′(t_{i}^{*})‖\,\Delta t_i. \nonumber \]
Voir la figure\(\PageIndex{4}\).
Notez que
\[\lim_{n\to\infty}\sum_{i=1}^{n} f(\vecs r(t_i^*))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i=\int_a^b f(\vecs r(t))‖\vecs r′(t)‖\,dt. \nonumber \]
En d'autres termes, lorsque la largeur des intervalles\([t_{i−1},t_i]\) se réduit à zéro, la somme\(\displaystyle \sum_{i=1}^{n} f(\vecs r(t_i^{*}))‖\vecs r′(t_{i}^{*})‖\,\Delta t_i\) converge vers l'intégrale\(\displaystyle \int_{a}^{b}f(\vecs r(t))‖\vecs r′(t)‖\,dt\). Nous avons donc le théorème suivant.
\(f\)Soit une fonction continue avec un domaine qui inclut la courbe lisse\(C\) avec paramétrage\(\vecs r(t)\),\(a≤t≤b\). Alors
\[\int_C f \,ds=\int_{a}^{b} f(\vecs r(t))‖\vecs r′(t)‖\,dt.\label{scalerLineInt1} \]
Bien que nous ayons étiqueté Equation \ ref {ApproxLineInteq1} en tant qu'équation, elle est plus précisément considérée comme une approximation car nous pouvons montrer que le côté gauche de l'équation \ ref {ApproxLineInteq1} s'approche du côté droit comme\(n\to\infty\). En d'autres termes, laisser les largeurs des pièces se réduire à zéro rend la somme de droite arbitrairement proche de la somme de gauche. Depuis
\[‖\vecs r′(t)‖=\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2}, \nonumber \]
nous obtenons le théorème suivant, que nous utilisons pour calculer les intégrales de lignes scalaires.
\(f\)Soit une fonction continue avec un domaine qui inclut la courbe lisse\(C\) avec paramétrage\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\),\(a≤t≤b\). Alors
\[\int_C f(x,y,z) \,ds=\int_{a}^{b} f(\vecs r(t))\sqrt{({x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt. \nonumber \]
De même,
\[\int_C f(x,y) \,ds=\int_{a}^{b}f(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2} \,dt \nonumber \]
si\(C\) est une courbe plane et\(f\) est fonction de deux variables.
Notez qu'une conséquence de ce théorème est l'équation\(ds=‖\vecs r′(t)‖ \,dt\). En d'autres termes, la modification de la longueur de l'arc peut être considérée comme une modification du\(t\) domaine, mise à l'échelle selon l'amplitude du vecteur\(\vecs r′(t)\).
Détermine la valeur de l'intégrale\(\displaystyle \int_C(x^2+y^2+z) \,ds\), où\(C\) fait partie de l'hélice paramétrée par\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤2\pi\).
Solution
Pour calculer une intégrale scalaire, nous commençons par convertir la variable d'intégration de la longueur de l'arc\(s\) en\(t\). Ensuite, nous pouvons utiliser l'équation \ ref {eq12a} pour calculer l'intégrale par rapport à\(t\). Notez que
\[f(\vecs r(t))={\cos}^2 t+{\sin}^2 t+t=1+t \nonumber \]
et
\[\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} =\sqrt{{(−\sin(t))}^2+{\cos}^2(t)+1} =\sqrt{2}.\nonumber \]
Par conséquent,
\[\int_C(x^2+y^2+z) \,ds=\int_{0}^{2\pi} (1+t)\sqrt{2} \,dt. \nonumber \]
Notez que l'équation \ ref {eq12a} a traduit l'intégrale de la ligne difficile d'origine en une intégrale à variable unique gérable. Depuis
\ [\ begin {align*} \ int_ {0} ^ {2 \ pi} (1+t) \ sqrt {2} \, dt &= {\ left [\ sqrt {2} t+ \ dfrac {\ sqrt {2} t^2} {2} \ right]} _ {0} ^ {2 \ pi} \ \ [4 points] &=2 \ sqrt {2} \ right]} _ {0} ^ {
2 \ pi} \ [4 points] &=2 \ sqrt {2} \ pi+2 \ sqrt {2} {\ pi} ^2, \ end {align*} \]
nous avons
\[\int_C(x^2+y^2+z) \,ds=2\sqrt{2}\pi+2\sqrt{2}{\pi}^2. \nonumber \]
Evaluer\(\displaystyle \int_C(x^2+y^2+z)ds\), où C est la courbe avec paramétrage\(\vecs r(t)=⟨\sin(3t),\cos(3t)⟩\),\(0≤t≤\dfrac{\pi}{4}\).
- Allusion
-
Utilisez la version à deux variables de la définition intégrale de la ligne scalaire (équation \ ref {eq13}).
- Réponse
-
\[\dfrac{1}{3}+\dfrac{\sqrt{2}}{6}+\dfrac{3\pi}{4} \nonumber \]
Détermine la valeur de l'intégrale\(\displaystyle \int_C(x^2+y^2+z) \,ds\), où\(C\) fait partie de l'hélice paramétrée par\(\vecs r(t)=⟨\cos(2t),\sin(2t),2t⟩\),\(0≤t≤π\). Notez que cette fonction et cette courbe sont les mêmes que dans l'exemple précédent ; la seule différence est que la courbe a été reparamétrée de telle sorte que le temps s'écoule deux fois plus vite.
Solution
Comme dans l'exemple précédent, nous utilisons l'équation \ ref {eq12a} pour calculer l'intégrale par rapport à\(t\). Notez que\(f(\vecs r(t))={\cos}^2(2t)+{\sin}^2(2t)+2t=2t+1\) et
\ [\ begin {align*} \ sqrt {{(x′ (t))} ^2+ {(y′ (t))} ^2+ {(z′ (t))} ^2} &= \ sqrt {(− \ sin t+ \ cos t+4)} \ \ [4 points] &=22
\ end {align*} \]
nous avons donc
\[\begin{align*} \int_C(x^2+y^2+z)ds &=2\sqrt{2}\int_{0}^{\pi}(1+2t)dt\\[4pt] &=2\sqrt{2}\Big[t+t^2\Big]_0^{\pi} \\[4pt] &=2\sqrt{2}(\pi+{\pi}^2). \end{align*}\]
Notez que cela correspond à la réponse de l'exemple précédent. La modification du paramétrage n'a pas modifié la valeur de l'intégrale linéaire. Les intégrales des lignes scalaires sont indépendantes du paramétrage, à condition que la courbe soit parcourue exactement une fois par le paramétrage.
Évaluez l'intégrale de la ligne\(\displaystyle \int_C(x^2+yz) \,ds\), où\(C\) se trouve la ligne avec paramétrage\(\vecs r(t)=⟨2t,5t,−t⟩\),\(0≤t≤10\). Reparamétrez C avec le paramétrage\(s(t)=⟨4t,10t,−2t⟩\)\(0≤t≤5\), recalculez l'intégrale\(\displaystyle \int_C(x^2+yz) \,ds\) de la ligne et notez que le changement de paramétrage n'a eu aucun effet sur la valeur de l'intégrale.
- Allusion
-
Utilisez l'équation \ ref {eq12a}.
- Réponse
-
Les deux intégrales de ligne sont égales\(−\dfrac{1000\sqrt{30}}{3}\).
Maintenant que nous pouvons évaluer les intégrales des lignes, nous pouvons les utiliser pour calculer la longueur de l'arc. Si\(f(x,y,z)=1\), alors
\[\begin{align*} \int_C f(x,y,z) \,ds &=\lim_{n\to\infty} \sum_{i=1}^{n} f(t_{i}^{*}) \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \sum_{i=1}^{n} \,\Delta s_i \\[4pt] &=\lim_{n\to\infty} \text{length} (C)\\[4pt] &=\text{length} (C). \end{align*}\]
Par conséquent,\(\displaystyle \int_C 1 \,ds\) est la longueur de l'arc de\(C\).
Un fil a une forme qui peut être modélisée avec le paramétrage\(\vecs r(t)=⟨\cos t,\sin t,\frac{2}{3} t^{3/2}⟩\),\(0≤t≤4\pi\). Détermine la longueur du fil.
Solution
La longueur du fil est donnée par\(\displaystyle \int_C 1 \,ds\), où\(C\) est la courbe avec paramétrage\(\vecs r\). Par conséquent,
\[\begin{align*} \text{The length of the wire} &=\int_C 1 \,ds \\[4pt] &=\int_{0}^{4\pi} ||\vecs r′(t)||\,dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{(−\sin t)^2+\cos^2 t+t}dt \\[4pt] &=\int_{0}^{4\pi} \sqrt{1+t} dt \\[4pt] &=\left.\dfrac{2{(1+t)}^{\frac{3}{2}}}{3} \right|_{0}^{4\pi} \\[4pt] &=\frac{2}{3}\left((1+4\pi)^{3/2}−1\right). \end{align*}\]
Trouvez la longueur d'un fil avec paramétrage\(\vecs r(t)=⟨3t+1,4−2t,5+2t⟩\),\(0≤t≤4\).
- Allusion
-
Détermine l'intégrale droite de l'un sur la courbe correspondante.
- Réponse
-
\(4\sqrt{17}\)
Intégrales de lignes vectorielles
Le deuxième type d'intégrales linéaires sont les intégrales de lignes vectorielles, dans lesquelles nous les intégrons le long d'une courbe à travers un champ vectoriel. Par exemple, laissez
\[\vecs F(x,y,z)=P(x,y,z)\,\hat{\mathbf i}+Q(x,y,z)\,\hat{\mathbf j}+R(x,y,z)\,\hat{\mathbf k} \nonumber \]
être un champ vectoriel continu\(ℝ^3\) qui représente une force sur une particule, et\(C\) soit une courbe lisse\(ℝ^3\) contenue dans le domaine de\(\vecs F\). Comment calculerait-on le travail effectué\(\vecs F\) en déplaçant une particule\(C\) ?
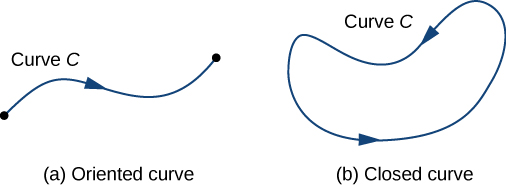
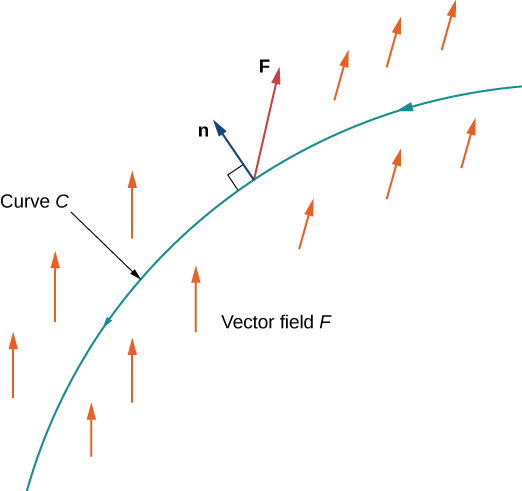
Pour répondre à cette question, notez d'abord qu'une particule peut se déplacer dans deux directions le long d'une courbe : une direction vers l'avant et une vers l'arrière. Le travail effectué par le champ vectoriel dépend de la direction dans laquelle la particule se déplace. Par conséquent, nous devons spécifier une direction le long de la courbe\(C\) ; une telle direction spécifiée est appelée orientation d'une courbe. La direction spécifiée est la direction positive le long\(C\) ; la direction opposée est la direction négative le long\(C\). Quand on lui\(C\) a donné une orientation,\(C\) on parle de courbe orientée (Figure\(\PageIndex{5}\)). Le travail effectué sur la particule dépend de la direction dans laquelle la particule se déplace le long de la courbe.
Une courbe fermée est une courbe pour laquelle il existe un paramétrage\(\vecs r(t)\)\(a≤t≤b\), tel que\(\vecs r(a)=\vecs r(b)\), et la courbe est parcourue exactement une fois. En d'autres termes, le paramétrage se fait de manière individuelle sur le domaine\((a,b)\).
\(\vecs r(t)\)Soit un paramétrage de\(C\) for\(a≤t≤b\) tel que la courbe soit parcourue exactement une fois par la particule et que la particule se déplace dans la direction positive\(C\). Divisez l'intervalle de paramètres\([a,b]\) en n sous-intervalles\([t_{i−1},t_i]\)\(0≤i≤n\),, de largeur égale. Désignez les points de terminaison de\(r(t_0)\)\(r(t_1)\),,...,\(r(t_n)\) par\(P_0\),...,\(P_n\). Points\(P_i\)\(C\) divisés en n morceaux. Indique la longueur de la pièce de\(P_{i−1}\)\(P_i\) à\(\Delta s_i\). Pour chacun d'entre eux\(i\), choisissez une valeur\(t_i^*\) dans le sous-intervalle\([t_{i−1},t_i]\). Ensuite, le point final de\(\vecs r(t_i^*)\) est un point situé dans la partie\(C\) comprise entre\(P_{i−1}\) et\(P_i\) (Figure\(\PageIndex{6}\)). Si elle\(\Delta s_i\) est petite, alors que la particule se déplace de\(P_{i−1}\) vers\(P_i\) le long\(C\), elle se déplace approximativement dans la direction de\(\vecs T(P_i)\), le vecteur tangent unitaire à l'extrémité de\(\vecs r(t_i^*)\). \(P_i^*\)Dénotons le point final de\(\vecs r(t_i^*)\). Ensuite, le travail effectué par le champ vectoriel de force pour déplacer la particule de\(P_{i−1}\) à\(P_i\) est\(\vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))\), de sorte que le travail total effectué\(C\) est
\[\sum_{i=1}^n \vecs F(P_i^*)·(\Delta s_i \vecs T(P_i^*))=\sum_{i=1}^n \vecs F(P_i^*)·\vecs T(P_i^*)\,\Delta s_i. \nonumber \]
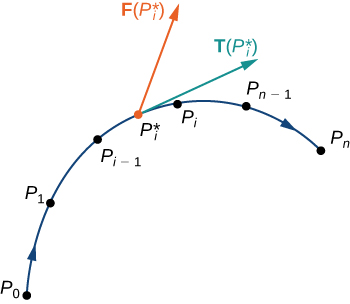
Laisser la longueur de l'arc des pièces\(C\) devenir arbitrairement petite en prenant une limite, ce\(n\rightarrow \infty\) qui nous donne le travail effectué par le champ pour déplacer la particule\(C\). Par conséquent, le travail effectué\(\vecs{F}\) en déplaçant la particule dans la direction positive\(C\) est défini comme
\[W=\int_C \vecs{F} \cdot \vecs{T}\,ds, \nonumber \]
ce qui nous donne le concept d'une droite vectorielle intégrale.
L'intégrale de la ligne vectorielle du champ vectoriel\(\vecs{F}\) le long de la courbe lisse orientée\(C\) est
\[\int_C \vecs{F} \cdot \vecs{T}\, ds=\lim_{n\to\infty} \sum_{i=1}^{n} \vecs{F}(P_i^*) \cdot \vecs{T}(P_i^*)\Delta s_i \nonumber \]
si cette limite existe.
Avec les intégrales de lignes scalaires, ni l'orientation ni le paramétrage de la courbe ne comptent. Tant que la courbe est parcourue exactement une fois par le paramétrage, la valeur de l'intégrale de la droite reste inchangée. Avec les intégrales de lignes vectorielles, l'orientation de la courbe est importante. Si nous considérons l'intégrale de la ligne comme un travail informatique, alors c'est logique : si vous gravissez une montagne, la force gravitationnelle de la Terre agit négativement sur vous. Si vous descendez la montagne par le même chemin, la force gravitationnelle de la Terre agit positivement sur vous. En d'autres termes, l'inversion de la trajectoire fait passer la valeur de travail de négative à positive dans ce cas. Notez que s'il s'\(C\)agit d'une courbe orientée, alors nous laissons\(−C\) représenter la même courbe mais avec une orientation opposée.
Comme pour les intégrales de lignes scalaires, il est plus facile de calculer une intégrale de ligne vectorielle si nous l'exprimons en termes de fonction de paramétrage\(\vecs{r}\) et de variable\(t\). Pour traduire l'intégrale\(\displaystyle \int_C \vecs{F} \cdot \vecs{T}ds\) en termes de\(t\), notez que\(\vecs{T}\) le vecteur tangent unitaire\(C\) est donné par\(\vecs{T}=\dfrac{\vecs{r}′(t)}{‖\vecs{r}′(t)‖}\) (en supposant\(‖\vecs{r}′(t)‖≠0\)). Puisque\(ds=‖\vecs r′(t)‖\,dt\), comme nous l'avons vu en discutant des intégrales de lignes scalaires, nous avons
\[\vecs F·\vecs T\,ds=\vecs F(\vecs r(t))·\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖}‖\vecs r′(t)‖dt=\vecs F(\vecs r(t))·\vecs r′(t)\,dt. \nonumber \]
Ainsi, nous avons la formule suivante pour calculer les intégrales de lignes vectorielles :
\[\int_C\vecs F·\vecs T\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs r′(t)\,dt.\label{lineintformula} \]
En raison de l'équation \ ref {lineintformula}, nous utilisons souvent la notation\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) pour l'intégrale de la ligne\(\displaystyle \int_C \vecs F·\vecs T\,ds\).
Si\(\vecs r(t)=⟨x(t),y(t),z(t)⟩\), alors\(\dfrac{d\vecs{r}}{dt}\) désigne un vecteur\(⟨x′(t),y′(t),z′(t)⟩\), et\(d\vecs{r} = \vecs r'(t)\,dt\).
Trouvez la valeur de l'intégrale\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), où\(C\) est le demi-cercle paramétré par\(\vecs{r}(t)=⟨\cos t,\sin t⟩\),\(0≤t≤\pi\) et\(\vecs F=⟨−y,x⟩\).
Solution
Nous pouvons utiliser l'équation \ ref {lineintformula} pour convertir la variable d'intégration de\(s\) à\(t\). Nous avons alors
\[\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩ \; \text{and} \; \vecs r′(t)=⟨−\sin t,\cos t⟩ . \nonumber \]
Par conséquent,
\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{\pi} {\sin}^2 t+{\cos}^2 t \,dt \\[4pt] &=\int_0^{\pi}1 \,dt=\pi.\end{align*}\]
Voir la figure\(\PageIndex{7}\).
Trouvez la valeur de l'intégrale\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), où\(C\) est le demi-cercle paramétré par\(\vecs r(t)=⟨\cos (t+π),\sin t⟩\),\(0≤t≤\pi\) et\(\vecs F=⟨−y,x⟩\).
Solution
Notez que c'est le même problème que Example\(\PageIndex{5}\), sauf que l'orientation de la courbe a été parcourue. Dans cet exemple, le paramétrage commence à\(\vecs r(0)=⟨-1,0⟩\) et se termine à\(\vecs r(\pi)=⟨1,0⟩\). Par l'équation \ ref {lineintformula},
\[\begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &=\int_0^{\pi} ⟨−\sin t,\cos (t+\pi)⟩·⟨−\sin (t+\pi), \cos t⟩dt\\[4pt] &=\int_0^{\pi}⟨−\sin t,−\cos t⟩·⟨\sin t,\cos t⟩dt\\[4pt] &=\int_{0}^{π}(−{\sin}^2 t−{\cos}^2 t)dt \\[4pt] &=\int_{0}^{\pi}−1dt\\[4pt] &=−\pi. \end{align*}\]
Notez que c'est la négative de la réponse de l'exemple\(\PageIndex{5}\). Il est logique que cette réponse soit négative car l'orientation de la courbe va à l'encontre du « flux » du champ vectoriel.
\(C\)Soit une courbe orientée et\(-C\) désignons la même courbe mais avec l'orientation inversée. Ensuite, les deux exemples précédents illustrent le fait suivant :
\[\int_{-C} \vecs{F} \cdot d\vecs{r}=−\int_C\vecs{F} \cdot d\vecs{r}. \nonumber \]
En d'autres termes, l'inversion de l'orientation d'une courbe modifie le signe d'une intégrale linéaire.
\(\vecs F=x\,\hat{\mathbf i}+y \,\hat{\mathbf j}\)Soit un champ vectoriel et\(C\) soit la courbe avec paramétrage\(⟨t,t^2⟩\) pour\(0≤t≤2\). Lequel est le plus grand :\(\displaystyle \int_C\vecs F·\vecs T\,ds\) ou\(\displaystyle \int_{−C} \vecs F·\vecs T\,ds\) ?
- Allusion
-
Imaginez que vous vous déplacez le long de la trajectoire et\(\vecs F·\vecs T\) que vous calculez le produit scalaire au fur
- Réponse
-
\[\int_C \vecs F·\vecs T \,ds \nonumber \]
Une autre notation standard pour l'intégrale\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\) est\(\displaystyle \int_C P\,dx+Q\,dy+R \,dz\). Dans cette notation\(P,\, Q\), et\(R\) sont des fonctions, que nous considérons\(d\vecs{r}\) comme des vecteurs\(⟨dx,dy,dz⟩\). Pour justifier cette convention, rappelons-le\(d\vecs{r}=\vecs T\,ds=\vecs r′(t) \,dt=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Par conséquent,
\[\vecs{F} \cdot d\vecs{r}=⟨P,Q,R⟩·⟨dx,dy,dz⟩=P\,dx+Q\,dy+R\,dz. \nonumber \]
Si\(d\vecs{r}=⟨dx,dy,dz⟩\), alors\(\dfrac{dr}{dt}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\), ce qui implique que\(d\vecs{r}=\left\langle\dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle\,dt\). Par conséquent
\[\begin{align} \int_C \vecs{F} \cdot d\vecs{r} &=\int_C P\,dx+Q\,dy+R\,dz \\[4pt] &=\int_a^b\left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right)\,dt. \label{eq14}\end{align} \]
Trouvez la valeur de l'intégrale\(\displaystyle \int_C z\,dx+x\,dy+y\,dz\), où\(C\) est la courbe paramétrée par\(\vecs r(t)=⟨t^2,\sqrt{t},t⟩\),\(1≤t≤4\).
Solution
Comme dans nos exemples précédents, pour calculer cette intégrale linéaire, nous devons effectuer un changement de variables pour tout écrire en termes de\(t\). Dans ce cas, l'équation \ ref {eq14} nous permet d'effectuer cette modification :
\[\begin{align*} \int_C z\,dx+x\,dy+y\,dz &=\int_1^4 \left(t(2t)+t^2\left(\frac{1}{2\sqrt{t}}\right)+\sqrt{t}\right)\,dt \\[4pt] &=\int_1^4\left(2t^2+\frac{t^{3/2}}{2}+\sqrt{t}\right)\,dt \\[4pt] &={\left[\dfrac{2t^3}{3}+\dfrac{t^{5/2}}{5}+\dfrac{2t^{3/2}}{3} \right]}_{t=1}^{t=4} \\[4pt] &=\dfrac{793}{15}.\end{align*}\]
Trouvez la valeur de\(\displaystyle \int_C 4x\,dx+z\,dy+4y^2\,dz\), où se\(C\) trouve la courbe paramétrée par\(\vecs r(t)=⟨4\cos(2t),2\sin(2t),3⟩\),\(0≤t≤\dfrac{\pi}{4}\).
- Allusion
-
Écrivez l'intégrale en\(t\) utilisant l'équation \ ref {eq14}.
- Réponse
-
\(−26\)
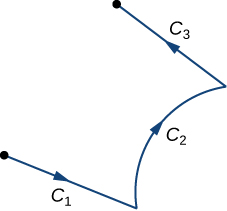
Nous avons appris à intégrer des courbes lisses et orientées. Supposons maintenant qu'il\(C\) s'agit d'une courbe orientée qui n'est pas lisse, mais qui peut être écrite comme l'union d'un nombre fini de courbes lisses. Dans ce cas, nous disons qu'il\(C\) s'agit d'une courbe lisse par morceaux. Pour être précis, une courbe\(C\) est lisse par morceaux si elle\(C\) peut être écrite comme une union de n courbes lisses\(C_1\),,...\(C_2\), de\(C_n\) telle sorte que l'extrémité de\(C_i\) soit le point de départ de\(C_{i+1}\) (Figure\(\PageIndex{8}\)). Lorsque les courbes\(C_i\) satisfont à la condition que l'extrémité de\(C_i\) soit le point de départ\(C_{i+1}\), nous écrivons leur union sous la forme\(C_1+C_2+⋯+C_n\).
Le théorème suivant résume plusieurs propriétés clés des intégrales de lignes vectorielles.
Soient\(\vecs F\)\(\vecs G\) des champs vectoriels continus dont les domaines incluent la courbe lisse orientée\(C\). Alors
- \(\displaystyle \int_C(\vecs F+\vecs G)·d\vecs{r}=\int_C \vecs{F} \cdot d\vecs{r}+\int_C \vecs G·d\vecs{r}\)
- \(\displaystyle \int_C k\vecs{F} \cdot d\vecs{r}=k\int_C \vecs{F} \cdot d\vecs{r}\), où\(k\) est une constante
- \(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=\int_{−C}\vecs{F} \cdot d\vecs{r}\)
- Supposons plutôt qu'il\(C\) s'agisse d'une courbe lisse par morceaux dans les domaines de\(\vecs F\) et\(\vecs G\), où\(C=C_1+C_2+⋯+C_n\) et\(C_1,C_2,…,C_n\) sont des courbes lisses, dont l'extrémité\(C_i\) est le point de départ de\(C_{i+1}\). Alors
\[\int_C \vecs F·d\vecs{r}=\int_{C_1} \vecs F·d\vecs{r}+\int_{C_2} \vecs F·d\vecs{r}+⋯+\int_{C_n} \vecs F·d\vecs{r}. \nonumber \]
Notez les similitudes entre ces éléments et les propriétés des intégrales à variable unique. Les propriétés i. et ii. indiquent que les intégrales linéaires sont linéaires, ce qui est également vrai pour les intégrales à variable unique. La propriété iii. indique que l'inversion de l'orientation d'une courbe modifie le signe de l'intégrale. Si nous considérons l'intégrale comme le calcul du travail effectué sur une particule qui se déplace\(C\), alors cela a du sens. Si la particule se déplace vers l'arrière plutôt que vers l'avant, alors la valeur du travail effectué a le signe opposé. Ceci est analogue à l'équation\(\displaystyle \int_a^b f(x)\,dx=−\int_b^af(x)\,dx\). Enfin, si\([a_1,a_2]\)\([a_2,a_3]\),...,\([a_{n−1},a_n]\) sont des intervalles, alors
\[\int_{a_1}^{a_n}f(x) \,dx=\int_{a_1}^{a_2}f(x)\,dx+\int_{a_1}^{a_3}f(x)\,dx+⋯+\int_{a_{n−1}}^{a_n} f(x)\,dx, \nonumber \]
ce qui est analogue à la propriété iv.
Trouvez la valeur de l'intégrale\(\displaystyle \int_C \vecs F·\vecs T \,ds\), où\(C\) est le rectangle (orienté dans le sens antihoraire) dans un plan avec des sommets\((0,0)\)\((2,0)\),\((2,1)\), et\((0,1)\), et où\(\vecs F=⟨x−2y,y−x⟩\) (Figure\(\PageIndex{9}\)).

Solution
Notez que la courbe\(C\) est l'union de ses quatre côtés, et que chaque côté est lisse. Il\(C\) est donc lisse par morceaux. \(C_1\)Représentons le côté de\((0,0)\) à\((2,0)\),\(C_2\) représentons le côté de\((2,0)\) à\((2,1)\),\(C_3\) représentons le côté de\((2,1)\) à\((0,1)\) et\(C_4\) représentons le côté de\((0,1)\) à\((0,0)\) (Figure\(\PageIndex{9}\)). Ensuite,
\[\int_C \vecs F·\vecs T \,dr=\int_{C_1} \vecs F·\vecs T \,dr+\int_{C_2} \vecs F·\vecs T \,dr+\int_{C_3} \vecs F·\vecs T \,dr+\int_{C_4} \vecs F·\vecs T \,dr. \nonumber \]
Nous voulons calculer chacune des quatre intégrales sur le côté droit à l'aide de l'équation \ ref {eq12a}. Avant cela, nous avons besoin d'un paramétrage de chaque côté du rectangle. Voici quatre paramétrisations (notez qu'elles se déplacent dans\(C\) le sens antihoraire) :
\[\begin{align*} C_1&: ⟨t,0⟩,0≤t≤2\\[4pt] C_2&: ⟨2,t⟩, 0≤t≤1 \\[4pt] C_3&: ⟨2−t,1⟩, 0≤t≤2\\[4pt] C_4&: ⟨0,1−t⟩, 0≤t≤1. \end{align*}\]
Par conséquent,
\[\begin{align*} \int_{C_1} \vecs F·\vecs T \,dr &=\int_0^2 \vecs F(\vecs r(t))·\vecs r′(t) \,dt \\[4pt] &=\int_0^2 ⟨t−2(0),0−t⟩·⟨1,0⟩ \,dt=\int_0^2 t \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}\Big]_0^2=2. \end{align*}\]
Notez que la valeur de cette intégrale est positive, ce qui ne devrait pas être surprenant. Lorsque nous nous déplaçons le long d'une courbe\(C_1\) de gauche à droite, notre mouvement s'effectue dans la direction générale du champ vectoriel lui-même. En tout point le long de la courbe\(C_1\), le vecteur tangent à la courbe et le vecteur correspondant dans le champ forment un angle inférieur à 90°. Par conséquent, le vecteur tangent et le vecteur de force ont un produit scalaire positif tout au long\(C_1\), et l'intégrale de la droite aura une valeur positive.
Les calculs pour les trois autres intégrales de ligne sont effectués de la même manière :
\[\begin{align*} \int_{C_2} \vecs{F} \cdot d\vecs{r} &=\int_{0}^{1}⟨2−2t,t−2⟩·⟨0,1⟩ \,dt \\[4pt] &=\int_{0}^{1} (t−2) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−2t\Big]_0^1=−\dfrac{3}{2}, \end{align*}\]
\[\begin{align*} \int_{C_3} \vecs F·\vecs T \,ds &=\int_0^2⟨(2−t)−2,1−(2−t)⟩·⟨−1,0⟩ \,dt \\[4pt] &=\int_0^2t \,dt=2, \end{align*}\]
et
\[\begin{align*} \int_{C_4} \vecs{F} \cdot d\vecs{r} &=\int_0^1⟨−2(1−t),1−t⟩·⟨0,−1⟩ \,dt \\[4pt] &=\int_0^1(t−1) \,dt \\[4pt] &=\Big[\tfrac{t^2}{2}−t\Big]_0^1=−\dfrac{1}{2}. \end{align*}\]
Ainsi, nous avons\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}=2\).
Calculez l'intégrale de la ligne\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\), où\(\vecs F\)\(C\) se trouve le champ vectoriel\(⟨y^2,2xy+1⟩\) et un triangle avec des sommets\((0,0)\)\((4,0)\), et\((0,5)\), orienté dans le sens antihoraire.
- Allusion
-
Écrivez le triangle comme l'union de ses trois côtés, puis calculez trois intégrales de ligne distinctes.
- Réponse
-
0
Applications des intégrales de ligne
Les intégrales de lignes scalaires ont de nombreuses applications. Ils peuvent être utilisés pour calculer la longueur ou la masse d'un fil, la surface d'une feuille d'une hauteur donnée ou le potentiel électrique d'un fil chargé en fonction d'une densité de charge linéaire. Les intégrales de lignes vectorielles sont extrêmement utiles en physique. Ils peuvent être utilisés pour calculer le travail effectué sur une particule lorsqu'elle se déplace dans un champ de force, ou le débit d'un fluide sur une courbe. Ici, nous calculons la masse d'un fil à l'aide d'une intégrale scalaire et le travail effectué par une force à l'aide d'une intégrale linéaire vectorielle.
Supposons qu'un morceau de fil soit modélisé par la courbe C dans l'espace. La masse par unité de longueur (densité linéaire) du fil est une fonction continue\(\rho(x,y,z)\). Nous pouvons calculer la masse totale du fil en utilisant l'intégrale de la ligne scalaire\(\displaystyle \int_C \rho(x,y,z) \,ds\). La raison en est que la masse est la densité multipliée par la longueur, et donc la densité d'un petit morceau de fil peut être approximée\(\rho(x^*,y^*,z^*) \,\Delta s\) pour un point donné\((x^*,y^*,z^*)\) de la pièce. Laisser la longueur des pièces se réduire à zéro avec une limite donne la ligne intégrale\(\displaystyle \int_C \rho(x,y,z) \,ds\).
Calculez la masse d'un ressort sous la forme d'une courbe paramétrée par\(⟨t,2\cos t,2\sin t⟩\),\(0≤t≤\dfrac{\pi}{2}\), avec une fonction de densité donnée par\(\rho(x,y,z)=e^x+yz\) kg/m (Figure\(\PageIndex{10}\)).
Solution
Pour calculer la masse du ressort, il faut trouver la valeur de l'intégrale scalaire\(\displaystyle \int_C(e^x+yz)\,ds\), où se\(C\) trouve l'hélice donnée. Pour calculer cette intégrale, nous l'écrivons en\(t\) utilisant l'équation \ ref {eq12a} :
\[\begin{align*} \int_C \left(e^x+yz\right) \,ds &=\int_0^{\tfrac{\pi}{2}} \left((e^t+4\cos t\sin t)\sqrt{1+(−2\cos t)^2+(2\sin t)^2}\right)\,dt\\[4pt] &=\int_0^{\tfrac{\pi}{2}}\left((e^t+4\cos t\sin t)\sqrt{5}\right) \,dt \\[4pt] &=\sqrt{5}\Big[e^t+2\sin^2 t\Big]_{t=0}^{t=\pi/2}\\[4pt] &=\sqrt{5}(e^{\pi/2}+1). \end{align*}\]
Par conséquent, la masse est de\(\sqrt{5}(e^{\pi/2}+1)\) kg.
Calculez la masse d'un ressort en forme d'hélice paramétrée par\(\vecs r(t)=⟨\cos t,\sin t,t⟩\),\(0≤t≤6\pi\), avec une fonction de densité donnée par\(\rho (x,y,z)=x+y+z\) kg/m.
- Allusion
-
Calculez l'intégrale linéaire de\(\rho\) au-dessus de la courbe avec paramétrage\(\vecs r\).
- Réponse
-
\(18\sqrt{2}{\pi}^2\)kg
Lorsque nous avons défini pour la première fois les intégrales de lignes vectorielles, nous avons utilisé le concept de travail pour motiver la définition. Il n'est donc pas surprenant que le calcul du travail effectué par un champ vectoriel représentant une force soit une utilisation standard des intégrales de lignes vectorielles. Rappelez-vous que si un objet se déplace le long d'une courbe\(C\) dans un champ de force\(\vecs F\), le travail requis pour déplacer l'objet est donné par\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\).
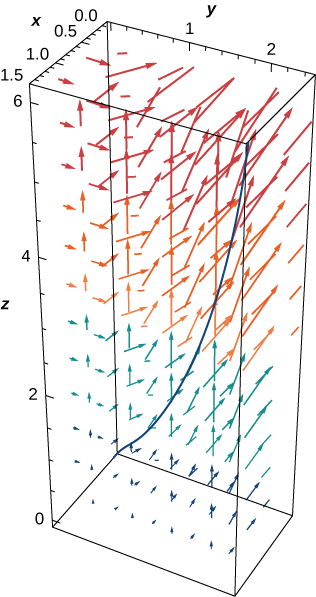
Combien de travail est nécessaire pour déplacer un objet dans un champ de force vectoriel\(\vecs F=⟨yz,xy,xz⟩\) le long de la trajectoire\(\vecs r(t)=⟨t^2,t,t^4⟩,\, 0≤t≤1?\) Voir Figure\(\PageIndex{11}\).
Solution
\(C\)Dénotons le chemin donné. Nous devons trouver la valeur de\(\displaystyle \int_C \vecs{F} \cdot d\vecs{r}\). Pour cela, nous utilisons l'équation \ ref {lineintformula} :
\[\begin{align*}\int_C \vecs{F} \cdot d\vecs{r} &=\int_0^1(⟨t^5,t^3,t^6⟩·⟨2t,1,4t^3⟩) \,dt \\[4pt] &=\int_0^1(2t^6+t^3+4t^9) \,dt \\[4pt] &={\Big[\dfrac{2t^7}{7}+\dfrac{t^4}{4}+\dfrac{2t^{10}}{5}\Big]}_{t=0}^{t=1}=\dfrac{131}{140}\;\text{units of work}. \end{align*}\]
Flux
Nous terminons cette section en abordant deux concepts clés liés aux intégrales linéaires : le flux à travers une courbe plane et la circulation le long d'une courbe plane. Le flux est utilisé dans les applications pour calculer le débit de fluide à travers une courbe, et le concept de circulation est important pour caractériser des champs de gradient conservateurs en termes d'intégrales de lignes. Ces deux concepts sont largement utilisés dans le reste de ce chapitre. L'idée de flux est particulièrement importante pour le théorème de Green et, dans les dimensions supérieures, pour le théorème de Stokes et le théorème de divergence.
\(C\)Soit une courbe plane et\(\vecs F\) soit un champ vectoriel dans le plan. Imagine\(C\) est une membrane à travers laquelle le fluide s'écoule, mais qui\(C\) ne gêne pas l'écoulement du fluide. En d'autres termes,\(C\) c'est une membrane idéalisée invisible pour le fluide. Supposons que cela\(\vecs F\) représente le champ de vitesse du fluide. Comment quantifier la vitesse à laquelle le fluide traverse\(C\) ?
Rappelez-vous que l'intégrale linéaire de\(\vecs F\) along\(C\) est,\(\displaystyle \int_C \vecs F·\vecs T \,ds\) en d'autres termes, l'intégrale de la ligne est le produit scalaire du champ vectoriel avec le vecteur tangentiel unitaire par rapport à la longueur de l'arc. Si nous remplaçons le vecteur tangentiel unitaire par le vecteur normal unitaire\(\vecs N(t)\) et que nous calculons plutôt l'intégrale\(\int_C \vecs F·\vecs N \,ds\), nous déterminons le flux transversal\(C\). Pour être précis, la définition de l'intégrale\(\displaystyle \int_C \vecs F·\vecs N \,ds\) est la même que celle de l'\(\vecs T\)intégrale\(\displaystyle \int_C \vecs F·\vecs T \,ds\), sauf que la somme de Riemann est remplacée par\(\vecs N\). Par conséquent, le flux transversal\(C\) est défini comme
\[\int_C \vecs F·\vecs N \,ds=\lim_{n\to\infty}\sum_{i=1}^{n} \vecs F(P_i^*)·\vecs N(P_i^*)\,\Delta s_i, \nonumber \]
où\(P_i^*\) et\(\Delta s_i\) sont définis tels qu'ils étaient pour Integral\(\displaystyle \int_C \vecs F·\vecs T \,ds\). Par conséquent, une intégrale de flux est une intégrale perpendiculaire à une intégrale de ligne vectorielle, car\(\vecs N\) et\(\vecs T\) sont des vecteurs perpendiculaires.
S'il s'\(\vecs F\)agit du champ de vitesse d'un fluide et\(C\) d'une courbe qui représente une membrane, alors le flux\(\vecs F\) transversal\(C\) est la quantité de fluide s'écoulant\(C\) par unité de temps, ou le débit.
Plus formellement,\(C\) soit une courbe plane paramétrée par\(\vecs r(t)=⟨x(t),\,y(t)⟩\),\(a≤t≤b\). \(\vecs n(t)=⟨y′(t),\,−x′(t)⟩\)Soit le vecteur qui est normal à l'\(C\)extrémité de\(\vecs r(t)\) et pointe vers la droite lorsque nous traversons\(C\) dans la direction positive (Figure\(\PageIndex{12}\)). Ensuite,\(\vecs N(t)=\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\) est le vecteur normal de l'unité\(C\) à l'extrémité de\(\vecs r(t)\) ce point vers la droite lorsque nous traversons\(C\).
Le flux\(\vecs F\) transversal\(C\) est une intégrale de la ligne
\[\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds. \nonumber \]
Nous donnons maintenant une formule pour calculer le flux sur une courbe. Cette formule est analogue à celle utilisée pour calculer l'intégrale d'une droite vectorielle (voir Équation \ ref {lineintformula}).
\(\vecs F\)Soit un champ vectoriel et\(C\) soit une courbe lisse avec paramétrage\(r(t)=⟨x(t),y(t)⟩\),\(a≤t≤b\) .Let\(\vecs n(t)=⟨y′(t),−x′(t)⟩\). Le flux de\(\vecs F\) croix\(C\) est
\[\int_C \vecs F·\vecs N\,ds=\int_a^b\vecs F(\vecs r(t))·\vecs n(t) \,dt. \label{eq84} \]
Avant de dériver la formule, notez que
\[‖\vecs n(t)‖=‖⟨y′(t),−x′(t)⟩‖=\sqrt{{(y′(t))}^2+{(x′(t))}^2}=‖\vecs r′(t)‖. \nonumber \]
Par conséquent,
\[\begin{align*}\int_C \vecs F·\vecs N \,ds &=\int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖} \,ds \\[4pt] &=\int_a^b \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}‖\vecs r′(t)‖ \,dt \\[4pt] &=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt. \end{align*}\]
\(\square\)
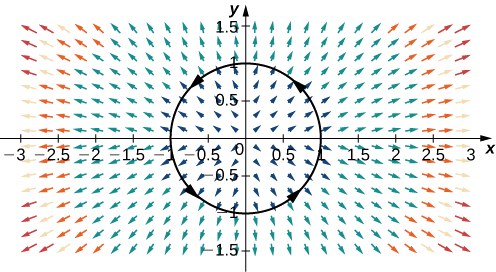
Calculez le flux de\(\vecs F=⟨2x,2y⟩\) à travers un cercle unitaire orienté dans le sens antihoraire (Figure\(\PageIndex{13}\)).
Solution
Pour calculer le flux, nous avons d'abord besoin d'un paramétrage de l'unité de cercle. Nous pouvons utiliser le paramétrage standard\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Le vecteur normal d'un cercle unitaire est\(⟨\cos t,\sin t⟩\). Par conséquent, le flux est
\[\begin{align*} \int_C \vecs F·\vecs N \,ds &=\int_0^{2\pi}⟨2\cos t,2\sin t⟩·⟨\cos t,\sin t⟩ \,dt\\[4pt] &=\int_0^{2\pi}(2{\cos}^2t+2{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi}({\cos}^2t+{\sin}^2t) \,dt \\[4pt] &=2\int_0^{2\pi} \,dt=4\pi.\end{align*}\]
Calculez le flux de part et d'\(\vecs F=⟨x+y,2y⟩\)autre du segment de droite de\((0,0)\) à\((2,3)\), où la courbe est orientée de gauche à droite.
- Allusion
-
Utilisez l'équation \ ref {eq84}.
- Réponse
-
\(3/2\)
\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩\)Soit un champ vectoriel bidimensionnel. Rappelez-vous que l'intégrale\(\displaystyle \int_C \vecs F·\vecs T \,ds\) s'écrit parfois sous la forme\(\displaystyle \int_C P\,dx+Q\,dy\). De manière analogue, le flux\(\displaystyle \int_C \vecs F·\vecs N \,ds\) est parfois écrit dans la notation\(\displaystyle \int_C −Q\,dx+P\,dy\), car le vecteur normal de l'unité\(\vecs N\) est perpendiculaire à la tangente unitaire\(\vecs T\). La rotation du vecteur\(d\vecs{r}=⟨dx,dy⟩\) de 90° produit un vecteur\(⟨dy,−dx⟩\). Par conséquent, l'intégrale de ligne dans Example\(\PageIndex{8}\) peut être écrite sous la forme\(\displaystyle \int_C −2y\,dx+2x\,dy\).
Circulation
Maintenant que nous avons défini le flux, nous pouvons nous concentrer sur la circulation. L'intégrale linéaire du champ vectoriel\(\vecs F\) le long d'une courbe fermée orientée est appelée circulation du\(\vecs F\) long\(C\). Les intégrales des lignes de circulation ont leur propre notation :\(\oint_C \vecs F·\vecs T \,ds\). Le cercle sur le symbole intégral indique qu'il\(C\) est « circulaire » en ce sens qu'il n'a pas d'extrémités. \(\PageIndex{5}\)L'exemple montre un calcul de la circulation.
Pour voir d'où vient le terme circulation et ce qu'il mesure,\(\vecs v\) représentons le champ de vitesse d'un fluide et\(C\) soit une courbe fermée orientée. À un point donné\(P\), plus la direction de\(\vecs v(P)\) est proche de la direction de\(\vecs T(P)\), plus la valeur du produit scalaire est élevée\(\vecs v(P)·\vecs T(P)\). La valeur maximale de\(\vecs v(P)·\vecs T(P)\) se produit lorsque les deux vecteurs pointent exactement dans la même direction ; la valeur minimale de\(\vecs v(P)·\vecs T(P)\) se produit lorsque les deux vecteurs pointent dans des directions opposées. Ainsi, la valeur de la circulation\(\oint_C \vecs v·\vecs T \,ds\) mesure la tendance du fluide à se déplacer dans la direction de\(C\).
\(\vecs F=⟨−y,\,x⟩\)Soit le champ vectoriel de l'exemple\(\PageIndex{3}\) et\(C\) représentons le cercle unitaire orienté dans le sens antihoraire. Calculez la circulation du\(\vecs F\) long\(C\).
Solution
Nous utilisons le paramétrage standard du cercle unitaire :\(\vecs r(t)=⟨\cos t,\sin t⟩\),\(0≤t≤2\pi\). Ensuite,\(\vecs F(\vecs r(t))=⟨−\sin t,\cos t⟩\) et\(\vecs r′(t)=⟨−\sin t,\cos t⟩\). Par conséquent, la circulation du\(\vecs F\) long\(C\) est
\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi}⟨−\sin t,\cos t⟩·⟨−\sin t,\cos t⟩ \,dt \\[4pt] &=\int_0^{2\pi} ({\sin}^2 t+{\cos}^2 t) \,dt \\[4pt] &=\int_0^{2\pi} \,dt=2\pi \;\text{units of work}. \end{align*}\]
Remarquez que la circulation est positive. La raison en est que l'orientation des\(C\) « flux » correspond à la direction de\(\vecs F\). En tout point du cercle, le vecteur tangent et le vecteur de\(\vecs F\) forme forment un angle inférieur à 90°, et le produit scalaire correspondant est donc positif.
Dans Exemple\(\PageIndex{12}\), et si nous avions orienté le cercle de l'unité dans le sens des aiguilles d'une montre ? Nous désignons le cercle unitaire orienté dans le sens des aiguilles d'une montre par\(−C\). Alors
\[\oint_{−C} \vecs F·\vecs T \,ds=−\oint_C \vecs F·\vecs T \,ds=−2\pi \;\text{units of work}. \nonumber \]
Notez que la circulation est négative dans ce cas. La raison en est que l'orientation de la courbe va à l'encontre de la direction de\(\vecs F\).
Calculez la circulation de\(\vecs F(x,y)=⟨−\dfrac{y}{x^2+y^2},\,\dfrac{x}{x^2+y^2}⟩\) le long d'un cercle unitaire orienté dans le sens antihoraire.
- Allusion
-
Utilisez l'équation \ ref {eq84}.
- Réponse
-
\(2\pi\)unités de travail
Calculez le travail effectué sur une particule qui traverse un cercle\(C\) de rayon 2 centré à l'origine, orienté dans le sens antihoraire, par champ\(\vecs F(x,y)=⟨−2,\,y⟩\). Supposons que la particule commence son mouvement à\((1,\,0)\).
Solution
Le travail effectué\(\vecs F\) sur la particule est la circulation du\(\vecs F\) long de\(C\) :\(\oint_C \vecs F·\vecs T \,ds\). Nous utilisons le paramétrage\(\vecs r(t)=⟨2\cos t,\,2\sin t⟩\),\(0≤t≤2\pi\) pour\(C\). Ensuite,\(\vecs r′(t)=⟨−2\sin t,\,2\cos t⟩\) et\(\vecs F(\vecs r(t))=⟨−2,\,2\sin t⟩\). Par conséquent, la circulation du\(\vecs F\) long\(C\) est
\[\begin{align*} \oint_C \vecs F·\vecs T \,ds &=\int_0^{2\pi} ⟨−2,2\sin t⟩·⟨−2\sin t,2\cos t⟩ \,dt\\[4pt] &=\int_0^{2\pi} (4\sin t+4\sin t\cos t) \,dt\\[4pt] &={\Big[−4\cos t+4{\sin}^2 t\Big]}_0^{2\pi}\\[4pt] &=\left(−4\cos(2\pi)+2{\sin}^2(2\pi)\right)−\left(−4\cos(0)+4{\sin}^2(0)\right)\\[4pt] &=−4+4=0\;\text{units of work}.\end{align*}\]
Le champ de force n'agit pas sur la particule.
Notez que la circulation du\(\vecs F\) long\(C\) est nulle. De plus, notez que puisque\(\vecs F\) est le gradient de\(f(x,y)=−2x+\dfrac{y^2}{2}\),\(\vecs F\) est conservateur. Nous démontrons dans une section ultérieure que dans certaines conditions générales, la circulation d'un champ vectoriel conservateur le long d'une courbe fermée est nulle.
Calculez le travail effectué par champ\(\vecs F(x,y)=⟨2x,\,3y⟩\) sur une particule qui traverse le cercle unitaire. Supposons que la particule commence son mouvement à\((−1,\,0)\).
- Allusion
-
Utilisez l'équation \ ref {eq84}.
- Réponse
-
\(0\)unités de travail
Concepts clés
- Les intégrales linéaires généralisent la notion d'intégrale à variable unique aux dimensions supérieures. Le domaine d'intégration dans une intégrale à variable unique est un segment de droite le long de\(x\) l'axe y, mais le domaine d'intégration dans une intégrale linéaire est une courbe dans un plan ou dans l'espace.
- Si\(C\) c'est une courbe, alors la longueur de\(C\) est\(\displaystyle \int_C \,ds\).
- Il existe deux types d'intégrales linéaires : les intégrales linéaires scalaires et les intégrales linéaires vectorielles. Les intégrales de lignes scalaires peuvent être utilisées pour calculer la masse d'un fil ; les intégrales de lignes vectorielles peuvent être utilisées pour calculer le travail effectué sur une particule traversant un champ.
- Les intégrales de lignes scalaires peuvent être calculées à l'aide de l'équation \ ref {eq12a} ; les intégrales de lignes vectorielles peuvent être calculées à l'aide de l'équation \ ref {lineintformula}.
- Deux concepts clés exprimés en termes d'intégrales de ligne sont le flux et la circulation. Le flux mesure la vitesse à laquelle un champ franchit une ligne donnée ; la circulation mesure la tendance d'un champ à se déplacer dans la même direction qu'une courbe fermée donnée.
Équations clés
- Calcul d'une intégrale scalaire
\(\displaystyle \int_C f(x,y,z) \,ds=\int_a^bf(\vecs r(t))\sqrt{{(x′(t))}^2+{(y′(t))}^2+{(z′(t))}^2} \,dt\) - Calcul d'une intégrale de ligne vectorielle
\(\displaystyle \int_C \vecs F·d\vecs{r}=\int_C \vecs F·\vecs T \,ds=\int_a^b\vecs F(\vecs r(t))·\vecs r′(t)\,dt\)
ou
\(\displaystyle \int_C P\,dx+Q\,dy+R\,dz=\int_a^b \left(P\big(\vecs r(t)\big)\dfrac{dx}{dt}+Q\big(\vecs r(t)\big)\dfrac{dy}{dt}+R\big(\vecs r(t)\big)\dfrac{dz}{dt}\right) \,dt\) - Calcul du flux
\(\displaystyle \int_C \vecs F·\dfrac{\vecs n(t)}{‖\vecs n(t)‖}\,ds=\int_a^b \vecs F(\vecs r(t))·\vecs n(t) \,dt\)
Lexique
- circulation
- la tendance d'un fluide à se déplacer dans le sens de la courbe\(C\). S'il s'\(C\)agit d'une courbe fermée, alors la circulation du\(\vecs F\) long\(C\) est une intégrale linéaire\(∫_C \vecs F·\vecs T \,ds\), que nous désignons également\(∮_C\vecs F·\vecs T \,ds\).
- courbe fermée
- une courbe pour laquelle il existe un paramétrage\(\vecs r(t), a≤t≤b\), tel que\(\vecs r(a)=\vecs r(b)\), et la courbe est parcourue exactement une fois
- flux
- le débit d'un fluide s'écoulant à travers une courbe dans un champ vectoriel ; le flux du champ vectoriel\(\vecs F\) à travers une courbe plane\(C\) est une intégrale linéaire\(∫_C \vecs F·\frac{\vecs n(t)}{‖\vecs n(t)‖} \,ds\)
- ligne intégrale
- intégrale d'une fonction le long d'une courbe dans un plan ou dans l'espace
- orientation d'une courbe
- l'orientation d'une courbe\(C\) est une direction spécifiée de\(C\)
- courbe lisse par morceaux
- une courbe orientée qui n'est pas lisse, mais qui peut être écrite comme l'union d'un nombre fini de courbes lisses
- droite scalaire intégrale
- l'intégrale scalaire d'une fonction\(f\) le long d'une courbe\(C\) par rapport à la longueur de l'arc est l'intégrale\(\displaystyle \int_C f\,ds\), c'est l'intégrale d'une fonction scalaire\(f\) le long d'une courbe dans un plan ou dans l'espace ; une telle intégrale est définie en termes de somme de Riemann, de même qu'une intégrale à variable unique
- intégrale de ligne vectorielle
- l'intégrale droite vectorielle du champ vectoriel\(\vecs F\) le long de la courbe\(C\) est l'intégrale du produit scalaire de\(\vecs F\) avec le vecteur tangent unitaire\(\vecs T\) de\(C\) par rapport à la longueur de l'arc,\(∫_C \vecs F·\vecs T\, ds\) ; une telle intégrale est définie en termes de somme de Riemann, similaire à une intégrale à variable unique


