Skip to main content
Global

16.1E : Exercices pour la section 16.1

  1. Last updated
  2. Save as PDF
  • Page ID
    197922

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Le domaine du champ vectoriel\(\vecs{F}=\vecs{F}(x,y)\) est un ensemble de points\((x,y)\) dans un plan, et la plage de\(\vecs F\) est un ensemble de quoi dans le plan ?

    Réponse
    Vecteurs

    Pour les exercices 2 à 4, déterminez si l'énoncé est vrai ou faux.

    2. \(\vecs{F}=⟨3x^2,1⟩\)Le champ vectoriel est un champ dégradé pour\(ϕ_1(x,y)=x^3+y\) et\(ϕ_2(x,y)=y+x^3+100.\)

    3. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)Le champ vectoriel est constant en direction et en amplitude sur un cercle unitaire.

    Réponse
    Faux

    4. \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\)Le champ vectoriel n'est ni un champ radial ni un champ de rotation.

    Pour les exercices 5 à 13, décrivez chaque champ vectoriel en dessinant certains de ses vecteurs.

    5. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)

    Réponse

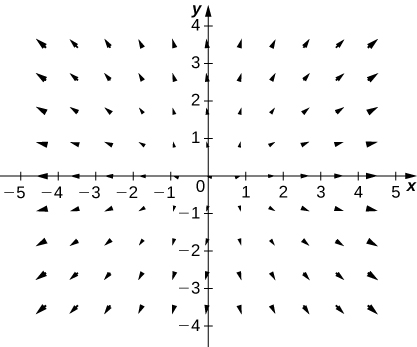
    clipboard_ed15464787a3931076aab028ddc5b12d7.png

    6. [T]\(\vecs{F}(x,y)=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

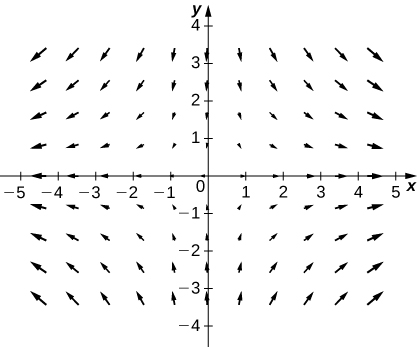
    7. [T]\(\vecs{F}(x,y)=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\)

    Réponse

    clipboard_ec0907b086839ad5c262019c65af7add7.png

    8. [T]\(\vecs{F}(x,y)=\,\hat{\mathbf i}+\,\hat{\mathbf j}\)

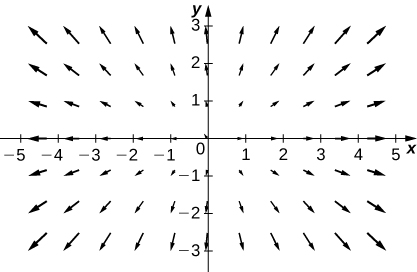
    9. [T]\(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}\)

    Réponse

    clipboard_ef331d6cd76b60efd3886d0df3b197637.png

    10. [T] \(\vecs{F}(x,y)=3\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

    11. [T]\(\vecs{F}(x,y)=y\,\hat{\mathbf i}+\sin x\,\hat{\mathbf j}\)

    Réponse

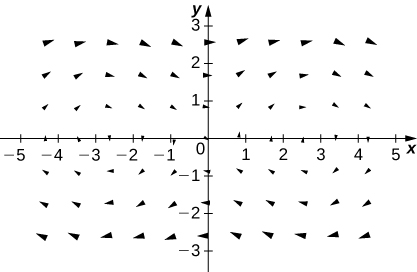
    clipboard_e90f52faea8df656c5e8538475924d4a3.png

    12. [T]\(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}+z\,\hat{\mathbf k}\)

    13. [T]\(\vecs F(x,y,z)=2x\,\hat{\mathbf i}−2y\,\hat{\mathbf j}−2z\,\hat{\mathbf k}\)

    Réponse

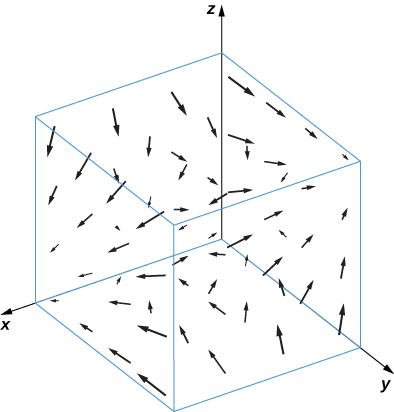
    clipboard_e1eb143e779ce49ea2a01af87d7a3548d.png

    14. [T]\(\vecs F(x,y,z)=yz\,\hat{\mathbf i}−xz\,\hat{\mathbf j}\)

    Pour les exercices 15 à 20, trouvez le champ vectoriel de gradient de chaque fonction\(f\).

    15. \(f(x,y)=x\sin y+\cos y\)

    Réponse
    \(\vecs{F}(x,y)=\sin(y)\,\hat{\mathbf i}+(x\cos y−\sin y)\,\hat{\mathbf j}\)

    16. \(f(x,y,z)=ze^{−xy}\)

    17. \(f(x,y,z)=x^2y+xy+y^2z\)

    Réponse
    \(\vecs F(x,y,z)=(2xy+y)\,\hat{\mathbf i}+(x^2+x+2yz)\,\hat{\mathbf j}+y^2\,\hat{\mathbf k}\)

    18. \(f(x,y)=x^2\sin(5y)\)

    19. \(f(x,y)=\ln(1+x^2+2y^2)\)

    Réponse
    \(\vecs{F}(x,y)=\dfrac{2x}{1+x^2+2y^2}\,\hat{\mathbf i}+\dfrac{4y}{1+x^2+2y^2}\,\hat{\mathbf j}\)

    20. \(f(x,y,z)=x\cos\left(\frac{y}{z}\right)\)

    21. Qu'est-ce qu'un champ vectoriel\(\vecs{F}(x,y)\) dont la\((x,y)\) valeur est une unité de longueur et pointe vers\((1,0)\) ?

    Réponse
    \(\vecs{F}(x,y)=\dfrac{(1−x)\,\hat{\mathbf i}−y\,\hat{\mathbf j}}{\sqrt{(1−x)^2+y^2}}\)

    Pour les exercices 22 à 24, écrivez des formules pour les champs vectoriels avec les propriétés données.

    22. Tous les vecteurs sont parallèles à l'\(x\)axe -et tous les vecteurs d'une ligne verticale ont la même amplitude.

    23. Tous les vecteurs pointent vers l'origine et ont une longueur constante.

    Réponse
    \(\vecs{F}(x,y)=\dfrac{(y\,\hat{\mathbf i}−x\,\hat{\mathbf j})}{\sqrt{x^2+y^2}}\)

    24. Tous les vecteurs ont une longueur unitaire et sont perpendiculaires au vecteur de position à ce point.

    25. Donnez une formule\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) pour le champ vectoriel dans un plan dont les propriétés sont tangentes\(\vecs{F}=\vecs 0\) au cercle\((0,0)\) et qui, en tout autre point,\((a,b), \vecs F\) sont tangentes au cercle\(x^2+y^2=a^2+b^2\) et pointent dans le sens des aiguilles d'une montre avec la magnitude\(\|\vecs F\|=\sqrt{a^2+b^2}\).

    Réponse
    \(\vecs{F}(x,y)=y\,\hat{\mathbf i}−x\,\hat{\mathbf j}\)

    26. Le champ vectoriel est-il\(\vecs{F}(x,y)=(P(x,y),Q(x,y))=(\sin x+y)\,\hat{\mathbf i}+(\cos y+x)\,\hat{\mathbf j}\) un champ dégradé ?

    27. Trouvez une formule pour le champ vectoriel\(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) étant donné que pour tous les points\((x,y)\), les\(\vecs F\) points pointent vers l'origine et\(\|\vecs F\|=\dfrac{10}{x^2+y^2}\).

    Réponse
    \(\vecs{F}(x,y)=\dfrac{−10}{(x^2+y^2)^{3/2}}(x\,\hat{\mathbf i}+y\,\hat{\mathbf j})\)

    Pour les exercices 28 à 29, supposons qu'un champ électrique dans le\(xy\) plan -provoqué par une ligne de charge infinie le long de\(x\) l'axe -est un champ de gradient avec une fonction potentielle\(V(x,y)=c\ln\left(\frac{r_0}{\sqrt{x^2+y^2}}\right)\), où\(c>0\)\(r_0\) est une constante et une distance de référence à laquelle le potentiel est supposé être nul.

    28. Trouvez les composantes du champ électrique dans les\(y\) directions\(x\) - et -, où\(\vecs E(x,y)=−\vecs ∇V(x,y).\)

    29. Montrez que le champ électrique en un point du\(xy\) plan est dirigé vers l'extérieur depuis l'origine et a une amplitude\(\|\vecs E\|=\dfrac{c}{r}\), où\(r=\sqrt{x^2+y^2}\).

    Réponse
    \(\|\vecs E\|=\dfrac{c}{|r|^2}r=\dfrac{c}{|r|}\dfrac{r}{|r|}\)

    Une ligne de flux (ou ligne droite) d'un champ vectoriel\(\vecs F\) est une courbe\(\vecs r(t)\) telle que\(d\vecs{r}/dt=\vecs F(\vecs r(t))\). Si\(\vecs F\) représente le champ de vitesse d'une particule en mouvement, les lignes de flux sont des trajectoires empruntées par la particule. Par conséquent, les lignes de flux sont tangentes au champ vectoriel.

    Pour les exercices 30 et 31, montrez que la courbe donnée\(\vecs c(t)\) est une ligne de flux du champ vectoriel de vitesse donné\(\vecs F(x,y,z)\).

    30. \(\vecs c(t)=⟨ e^{2t},\ln|t|,\frac{1}{t} ⟩,\,t≠0;\quad \vecs F(x,y,z)=⟨2x,z,−z^2⟩\)

    31. \(\vecs c(t)=⟨ \sin t,\cos t,e^t⟩;\quad \vecs F(x,y,z) =〈y,−x,z〉\)

    Réponse
    \(\vecs c′(t)=⟨ \cos t,−\sin t,e^{−t}⟩=\vecs F(\vecs c(t))\)

    Pour les exercices 32 à 34\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), laissez\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), et\(\vecs H=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\). \(\vecs F\)Correspondance\(\vecs G\), et\(\vecs H\) avec leurs graphiques.

    32.

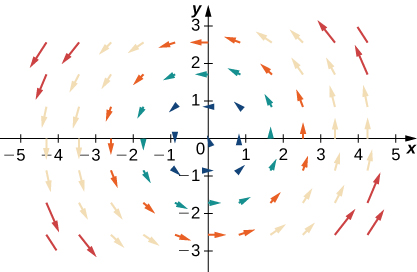
    clipboard_ed92420bb9a2a79bf7e0737bdf653eee9.png

    33.

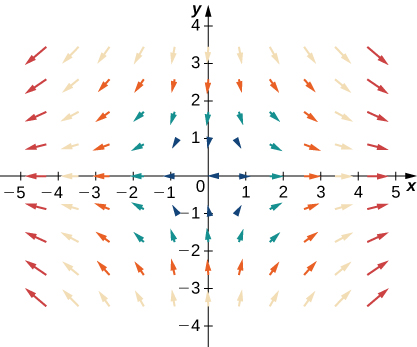
    clipboard_eb5a596effc35031ee81697fe6f857207.png

    Réponse
    \(\vecs H\)

    34.

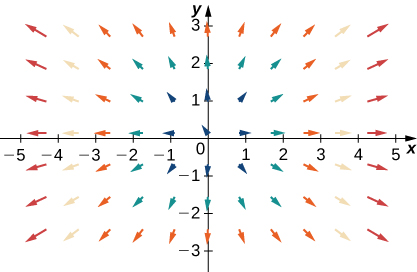
    clipboard_ec5488ed5d7cc242a516fe39456391eaa.png

    Pour les exercices 35 à 38\(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), laissez\(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), et\(\vecs H=−x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\). Faites correspondre les champs vectoriels à leurs graphes dans (I) − (IV).

    1. \(\vecs F+\vecs G\)
    2. \(\vecs F+\vecs H\)
    3. \(\vecs G+\vecs H\)
    4. \(−\vecs F+\vecs G\)

    35.

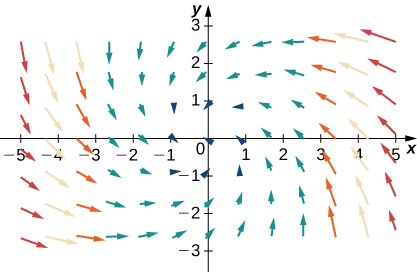
    clipboard_eddbf3f9c662003d8e6e632e520b53134.png

    Réponse
    d.\(−\vecs F+\vecs G\)

    36.

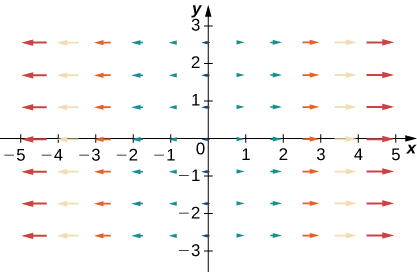
    clipboard_e75a38125572207465d05c29854873433.png

    37.

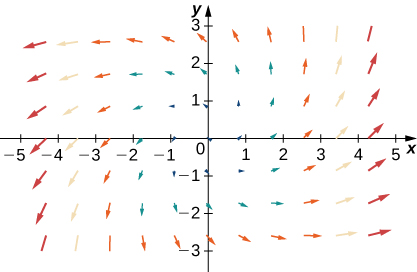
    clipboard_e0404b6b216ac76764fdd9b22d61f3e46.png

    Réponse
    un.\(\vecs F+\vecs G\)

    38.

    clipboard_e3db08e2f2eec3aeb28cd303fd451bb14.png