16.1 : Champs vectoriels
- Page ID
- 197911
- Reconnaissez un champ vectoriel dans un plan ou dans l'espace.
- Esquissez un champ vectoriel à partir d'une équation donnée.
- Identifier un champ conservateur et sa fonction potentielle associée.
Les champs vectoriels constituent un outil important pour décrire de nombreux concepts physiques, tels que la gravitation et l'électromagnétisme, qui influent sur le comportement des objets sur une grande région d'un plan ou de l'espace. Ils sont également utiles pour faire face à des comportements à grande échelle tels que les tempêtes atmosphériques ou les courants océaniques profonds. Dans cette section, nous examinons les définitions de base et les graphiques des champs vectoriels afin de pouvoir les étudier plus en détail dans la suite de ce chapitre.
Exemples de champs vectoriels
Comment modéliser la force gravitationnelle exercée par de multiples objets astronomiques ? Comment modéliser la vitesse des particules d'eau à la surface d'une rivière ? La figure\(\PageIndex{1}\) donne des représentations visuelles de tels phénomènes.
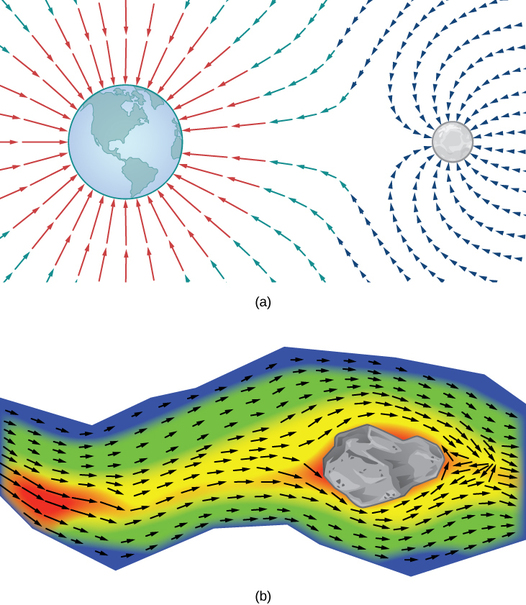
La figure\(\PageIndex{1a}\) montre un champ gravitationnel exercé par deux objets astronomiques, tels qu'une étoile et une planète ou une planète et une lune. En tout point de la figure, le vecteur associé à un point donne la force gravitationnelle nette exercée par les deux objets sur un objet d'unité de masse. Les vecteurs de plus grande magnitude sur la figure sont les vecteurs les plus proches de l'objet le plus grand. L'objet le plus gros a une masse plus grande, de sorte qu'il exerce une force gravitationnelle plus importante que l'objet plus petit.
La figure\(\PageIndex{1b}\) montre la vitesse d'une rivière à certains points de sa surface. Le vecteur associé à un point donné de la surface de la rivière donne la vitesse de l'eau à ce point. Comme les vecteurs situés à gauche de la figure sont de faible amplitude, l'eau s'écoule lentement sur cette partie de la surface. Lorsque l'eau se déplace de gauche à droite, elle rencontre des rapides autour d'un rocher. La vitesse de l'eau augmente et un tourbillon se produit dans une partie des rapides.
Chaque figure illustre un exemple de champ vectoriel. Intuitivement, un champ vectoriel est une carte de vecteurs. Dans cette section, nous étudions les champs vectoriels dans\(ℝ^2\) et\(ℝ^3\).
- Un champ vectoriel\(\vecs{F}\) dans\(ℝ^2\) est l'affectation d'un vecteur bidimensionnel\(\vecs{F}(x,y)\) à chaque point\((x,y)\) d'un sous-ensemble\(D\) de\(ℝ^2\). Le sous-ensemble\(D\) est le domaine du champ vectoriel.
- Un champ vectoriel\(\vecs{F}\) dans\(ℝ^3\) est l'affectation d'un vecteur tridimensionnel\(\vecs{F}(x,y,z)\) à chaque point\((x,y,z)\) d'un sous-ensemble\(D\) de\(ℝ^3\). Le sous-ensemble\(D\) est le domaine du champ vectoriel.
Champs vectoriels dans\(ℝ^2\)
Un champ vectoriel dans\(ℝ^2\) peut être représenté de deux manières équivalentes. La première méthode consiste à utiliser un vecteur dont les composantes sont des fonctions à deux variables :
\[\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩ \nonumber \]
La deuxième méthode consiste à utiliser les vecteurs unitaires standard :
\[\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}. \nonumber \]
Un champ vectoriel est dit continu si les fonctions qui le composent sont continues.
\(\vecs{F} (x,y)=(2y^2+x−4)\,\hat{\mathbf i}+\cos(x)\,\hat{\mathbf j}\)Soit un champ vectoriel dans\(ℝ^2\). Notez qu'il s'agit d'un exemple de champ vectoriel continu puisque les deux fonctions des composants sont continues. Quel vecteur est associé au point\((0,−1)\) ?
Solution
Remplacez les valeurs en points par\(x\) et\(y\) :
\[\begin{align*} \vecs{F} (0,-1) &=(2{(−1)}^2+0−4) \,\hat{\mathbf i}+\cos(0) \,\hat{\mathbf j} \\[4pt] &=−2 \,\hat{\mathbf i} + \hat{\mathbf j}. \end{align*}\]
\(\vecs{G}(x,y)=x^2y\,\hat{\mathbf i}−(x+y)\,\hat{\mathbf j}\)Soit un champ vectoriel dans\(ℝ^2\). Quel vecteur est associé au point\((−2,3)\) ?
- Allusion
-
Substituez les valeurs des points dans la fonction vectorielle.
- Réponse
-
\(\vecs{G}(−2,3)=12\hat{\mathbf i}−\hat{\mathbf j}\)
Dessiner un champ vectoriel
Nous pouvons désormais représenter un champ vectoriel en termes de composants de fonctions ou de vecteurs unitaires, mais le représenter visuellement en le dessinant est plus complexe car le domaine d'un champ vectoriel se trouve dans\(ℝ^2\), tout comme la plage. Par conséquent, le « graphe » d'un champ vectoriel\(ℝ^2\) vit dans un espace quadridimensionnel. Comme nous ne pouvons pas représenter visuellement un espace quadridimensionnel, nous dessinons des champs vectoriels\(ℝ^2\) dans un plan lui-même. Pour ce faire, dessinez le vecteur associé à un point donné au point d'un plan. Supposons, par exemple, que le vecteur associé au point\((4,−1)\) soit\(⟨3,1⟩\). Ensuite, nous dessinerions un vecteur\(⟨3,1⟩\) par point\((4,−1)\).
Nous devons tracer suffisamment de vecteurs pour voir la forme générale, mais pas trop pour que l'esquisse devienne un désordre. Si nous devions tracer le vecteur de l'image à chaque point de la région, cela remplirait complètement la région et serait inutile. Au lieu de cela, nous pouvons choisir des points aux intersections des lignes de la grille et tracer un échantillon de plusieurs vecteurs de chaque quadrant d'un système de coordonnées rectangulaires dans\(ℝ^2\).
Ce chapitre se concentre\(ℝ^2\) sur deux types de champs vectoriels : les champs radiaux et les champs rotatifs. Les champs radiaux modélisent certains champs gravitationnels et sources d'énergie, et les champs rotatifs modélisent le mouvement d'un fluide dans un vortex. Dans un champ radial, tous les vecteurs pointent directement vers ou loin de l'origine. De plus, l'amplitude d'un vecteur dépend uniquement de sa distance par rapport à l'origine. Dans un champ radial, le vecteur situé au point\((x,y)\) est perpendiculaire au cercle centré à l'origine qui contient le point\((x,y)\), et tous les autres vecteurs de ce cercle ont la même amplitude.
Esquissez le champ vectoriel\(\vecs{F} (x,y)=\dfrac{x}{2}\hat{\mathbf i}+\dfrac{y}{2}\hat{\mathbf j}\).
Solution
Pour esquisser ce champ vectoriel, choisissez un échantillon de points dans chaque quadrant et calculez le vecteur correspondant. Le tableau suivant donne un échantillon représentatif de points dans un plan et les vecteurs correspondants.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y) \) » style="vertical-align:middle ; « >\((1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
La figure\(\PageIndex{2a}\) montre le champ vectoriel. Pour vérifier que chaque vecteur est perpendiculaire au cercle correspondant, la figure\(\PageIndex{2b}\) montre des cercles superposés sur le champ vectoriel.
Dessine le champ radial\(\vecs{F} (x,y)=−\dfrac{x}{3}\hat{\mathbf i}−\dfrac{y}{3}\hat{\mathbf j}\).
- Allusion
-
Esquissez suffisamment de vecteurs pour vous faire une idée de la forme.
- Réponse
-

Contrairement aux champs radiaux, dans un champ de rotation, le vecteur au point\((x,y)\) est tangent (et non perpendiculaire) à un cercle de rayon\(r=\sqrt{x^2+y^2}\). Dans un champ de rotation standard, tous les vecteurs pointent soit dans le sens des aiguilles d'une montre, soit dans le sens antihoraire, et l'amplitude d'un vecteur dépend uniquement de sa distance par rapport à l'origine. Les deux exemples suivants sont des champs rotatifs dans le sens des aiguilles d'une montre, et leurs représentations visuelles montrent que les vecteurs semblent pivoter autour de l'origine.
Esquissez le champ vectoriel\(\vecs{F} (x,y)=⟨y,\,−x⟩\).
Solution
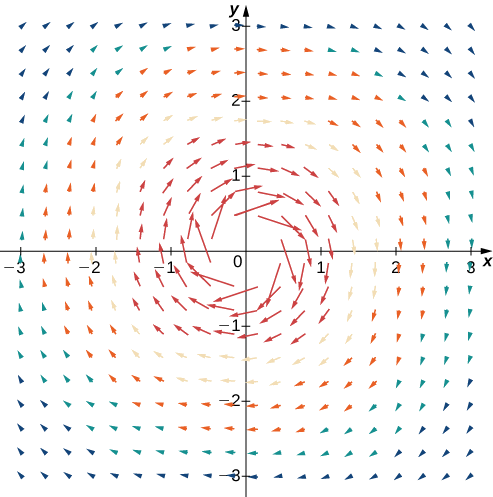
Créez un tableau (voir celui qui suit) en utilisant un échantillon représentatif de points dans un plan et leurs vecteurs correspondants. La figure\(\PageIndex{3}\) montre le champ vectoriel obtenu.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y) \) » style="vertical-align:middle ; « >\((1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−2⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨1,−1⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨2,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨1,1⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,2⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−1,1⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−2,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−1,−1⟩\) |
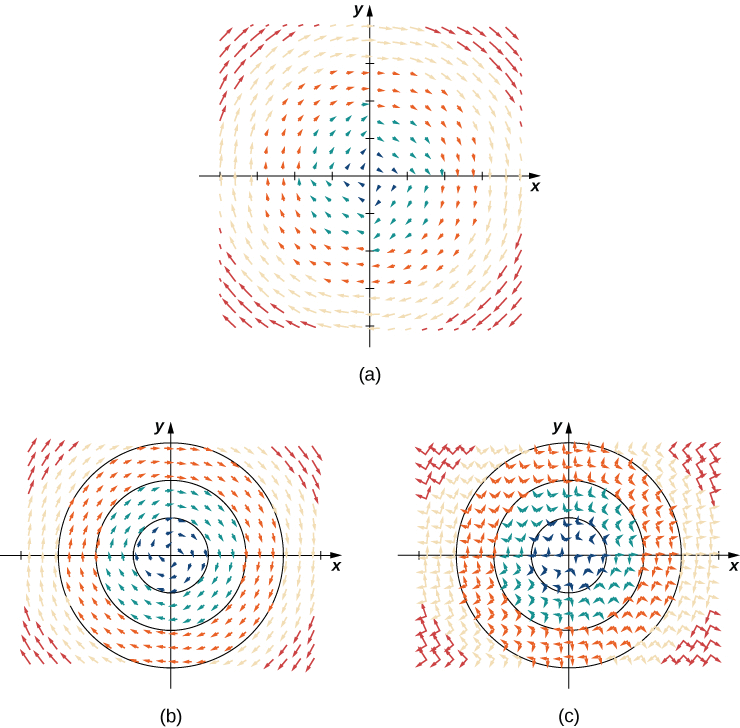
Analyse
Notez que le vecteur\(\vecs{F}(a,b)=⟨b,−a⟩\) pointe dans le sens des aiguilles d'une montre et est perpendiculaire au vecteur radial\(⟨a,b⟩\). (Nous pouvons vérifier cette assertion en calculant le produit scalaire des deux vecteurs :\(⟨a,b⟩·⟨−b,a⟩=−ab+ab=0\).) De plus, le vecteur\(⟨b,−a⟩\) a une longueur\(r=\sqrt{a^2+b^2}\). Nous avons donc une description complète de ce champ vectoriel de rotation : le vecteur associé au point\((a,b)\) est le vecteur de longueur r tangent au cercle de rayon r, et il pointe dans le sens des aiguilles d'une montre.
Des croquis tels que celui de la figure\(\PageIndex{3}\) sont souvent utilisés pour analyser les principaux systèmes orageux, y compris les ouragans et les cyclones. Dans l'hémisphère nord, les tempêtes tournent dans le sens antihoraire ; dans l'hémisphère sud, les tempêtes tournent dans le sens des aiguilles d'une montre. (Il s'agit d'un effet provoqué par la rotation de la Terre autour de son axe et s'appelle l'effet de Coriolis.)

Champ vectoriel d'esquisse\(\vecs{F}(x,y)=\dfrac{y}{x^2+y^2}\hat{\mathbf i}, -\dfrac{x}{x^2+y^2}\hat{\mathbf j}\).
Solution
Pour visualiser ce champ vectoriel, notez d'abord que le produit scalaire\(\vecs{F}(a,b)·(a \,\hat{\mathbf i}+b \,\hat{\mathbf j})\) est nul pour n'importe quel point\((a,b)\). Chaque vecteur est donc tangent au cercle sur lequel il se trouve. De plus, comme\((a,b)\rightarrow(0,0)\), la magnitude de\(\vecs{F}(a,b)\) passe à l'infini. Pour voir cela, notez que
\(||\vecs{F}(a,b)||=\sqrt{\dfrac{a^2+b^2}{ {(a^2+b^2)}^2 }} =\sqrt{\dfrac{1}{a^2+b^2}}\).
Depuis\(\dfrac{1}{a^2+b^2}\rightarrow \infty\)\((a,b)\rightarrow (0,0)\), puis\(||\vecs F(a,b)||\rightarrow \infty\) comme\((a,b)\rightarrow (0,0)\). Ce champ vectoriel ressemble au champ vectoriel de l'exemple\(\PageIndex{3}\), mais dans ce cas, les magnitudes des vecteurs proches de l'origine sont grandes. Le tableau\(\PageIndex{3}\) montre un échantillon de points et les vecteurs correspondants, et la figure\(\PageIndex{5}\) montre le champ vectoriel. Notez que ce champ vectoriel modélise le mouvement du tourbillon de la rivière dans la Figure\(\PageIndex{5}\) (b). Le domaine de ce champ vectoriel est entièrement égal\(ℝ^2\) à l'exception du point\((0,0)\).
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ ((x, y) \) » style="vertical-align:middle ; « >\((1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,−\dfrac{1}{2}⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,1⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−2,0)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨0,\dfrac{1}{2}⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((−1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−1,0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((0,−2)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},0⟩\) | \ ((x, y) \) » style="vertical-align:middle ; « >\((1,−1)\) | \ (\ vecs {F} (x, y) \) » style="vertical-align:middle ; « >\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Champ vectoriel d'esquisse\(\vecs{F}(x,y)=⟨−2y,\,2x⟩\). Le champ vectoriel est-il radial, rotationnel ou aucun des deux ?
- Allusion
-
Remplacez suffisamment de points\(\vecs{F}\) pour vous faire une idée de la forme.
- Réponse
-
Rotationnel

Supposons que\(\vecs{v} (x,y)=−\dfrac{2y}{x^2+y^2}\hat{\mathbf i}+\dfrac{2x}{x^2+y^2}\hat{\mathbf j}\) c'est le champ de vitesse d'un fluide. À quelle vitesse le fluide se déplace-t-il au point\((1,−1)\) ? (Supposons que les unités de vitesse soient des mètres par seconde.)
Solution
Pour déterminer la vitesse du fluide à un point\((1,−1)\), remplacez le point par\(\vecs{v} \) :
\(\vecs{v}(1,−1)=\dfrac{−2(−1)}{1+1}\hat{\mathbf i}+\dfrac{2(1)}{1+1}\hat{\mathbf j}=\hat{\mathbf i}+\hat{\mathbf j}\).
La vitesse du fluide à\((1,−1)\) est l'amplitude de ce vecteur. Par conséquent, la vitesse est de\(||\hat{\mathbf i}+\hat{\mathbf j}||=\sqrt{2}\) m/sec.
Le champ vectoriel\(\vecs{v} (x,y)=⟨4|x|,\,1⟩\) modélise la vitesse de l'eau à la surface d'une rivière. Quelle est la vitesse de l'eau au point\((2,3)\) ? Utilisez les mètres par seconde comme unités.
- Allusion
-
N'oubliez pas que la vitesse est l'amplitude de la vitesse.
- Réponse
-
\(\sqrt{65}\)m/sec
Nous avons examiné des champs de vecteurs contenant des vecteurs de différentes magnitudes, mais tout comme nous avons des vecteurs unitaires, nous pouvons également avoir un champ de vecteurs unitaires. Un champ vectoriel\(\vecs{F}\) est un champ vectoriel unitaire si l'amplitude de chaque vecteur du champ est de 1. Dans un champ de vecteurs unitaires, la seule information pertinente est la direction de chaque vecteur.
Afficher que le champ vectoriel\(\vecs{F} (x,y)=\left\langle\dfrac{y}{\sqrt{x^2+y^2}},−\dfrac{x}{\sqrt{x^2+y^2}}\right\rangle\) est un champ vectoriel unitaire.
Solution
Pour montrer qu'il\(\vecs{F}\) s'agit d'un champ unitaire, nous devons montrer que l'amplitude de chaque vecteur est\(1\). Notez que
\[\begin{align*} \sqrt{ \left(\dfrac{y}{\sqrt{x^2+y^2}}\right)^2+\left(−\dfrac{x}{\sqrt{x^2+y^2}}\right)^2} &=\sqrt{ \dfrac{y^2}{x^2+y^2}+\dfrac{x^2}{x^2+y^2}} \\[4pt] &=\sqrt{\dfrac{x^2+y^2}{x^2+y^2}} \\[4pt] &=1 \end{align*}\]
Il s'\(\vecs{F} \)agit donc d'un champ vectoriel unitaire.
Le champ vectoriel est-il\(\vecs{F} (x,y)=⟨−y,\,x⟩\) un champ vectoriel unitaire ?
- Allusion
-
Calculez la magnitude de\(\vecs{F} \) à un point arbitraire\((x,y)\).
- Réponse
-
Non.
Pourquoi les champs vectoriels unitaires sont-ils importants ? Supposons que nous étudions l'écoulement d'un fluide et que nous nous intéressions uniquement à la direction dans laquelle le fluide s'écoule à un point donné. Dans ce cas, la vitesse du fluide (qui est l'amplitude du vecteur de vitesse correspondant) n'est pas pertinente, car tout ce qui compte, c'est la direction de chaque vecteur. Par conséquent, le champ vectoriel unitaire associé à la vitesse est le champ que nous étudierions.
S'il s'\(\vecs{F} =⟨P,Q,R⟩\)agit d'un champ vectoriel, alors le champ vectoriel unitaire correspondant est\(\big\langle\tfrac{P}{||\vecs F||},\tfrac{Q}{||\vecs F||},\tfrac{R}{||\vecs F||}\big\rangle\). Notez que s'il s'\(\vecs{F}(x,y)=⟨y,\,−x⟩\)agit du champ vectoriel de l'exemple\(\PageIndex{6}\), alors l'amplitude de\(\vecs{F} \) est\(\sqrt{x^2+y^2}\), et donc le champ vectoriel unitaire correspondant est le champ\(\vecs{G} \) de l'exemple précédent.
S'il s'\(\vecs{F} \)agit d'un champ vectoriel, le processus de division\(\vecs{F} \) par sa magnitude pour former un champ vectoriel unitaire\(\vecs{F}/||\vecs{F}||\) est appelé normalisation du champ\(\vecs{F} \).
Champs vectoriels dans\(ℝ^3\)
Nous avons vu plusieurs exemples de champs vectoriels dans\(ℝ^2\) ; tournons maintenant notre attention vers les champs vectoriels dans\(ℝ^3\). Ces champs vectoriels peuvent être utilisés pour modéliser des champs gravitationnels ou électromagnétiques, et ils peuvent également être utilisés pour modéliser le flux de fluide ou le flux de chaleur en trois dimensions. Un champ vectoriel bidimensionnel ne peut réellement modéliser le mouvement de l'eau que sur une tranche bidimensionnelle d'une rivière (telle que la surface de la rivière). Comme une rivière traverse trois dimensions spatiales, pour modéliser le débit sur toute la profondeur de la rivière, nous avons besoin d'un champ vectoriel en trois dimensions.
La dimension supplémentaire d'un champ tridimensionnel peut rendre les champs vectoriels\(ℝ^3\) plus difficiles à visualiser, mais l'idée est la même. Pour visualiser un champ vectoriel dans\(ℝ^3\), tracez suffisamment de vecteurs pour montrer la forme globale. Nous pouvons utiliser une méthode similaire pour visualiser un champ vectoriel en\(ℝ^2\) choisissant des points dans chaque octant.
Tout comme pour les champs vectoriels dans\(ℝ^2\), nous pouvons représenter des champs vectoriels\(ℝ^3\) avec des fonctions de composants. Nous avons simplement besoin d'une fonction de composant supplémentaire pour la dimension supplémentaire. Nous écrivons soit
\[\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩ \nonumber \]
ou
\[\vecs{F}(x,y,z)=P(x,y,z)\hat{\mathbf i}+Q(x,y,z)\hat{\mathbf j}+R(x,y,z)\hat{\mathbf k}. \nonumber \]
Décrivez le champ vectoriel\(\vecs{F}(x,y,z)=⟨1,\,1,\,z⟩\).
Solution
Pour ce champ vectoriel, les\(y\) composantes\(x\) - et - sont constantes, de sorte que chaque point dans\(ℝ^3\) est associé à un vecteur avec des\(y\) composantes\(x\) - et - égales à un. Pour visualiser\(\vecs{F}\), nous examinons d'abord à quoi ressemble le champ dans le\(xy\) plan. Dans le\(xy\) plan,\(z=0\). Ainsi, chaque point du formulaire\((a,b,0)\) est\(⟨1,1,0⟩\) associé à un vecteur. Pour les points situés hors du\(xy\) plan mais légèrement au-dessus de celui-ci, le vecteur associé possède une\(z\) composante petite mais positive, et le vecteur associé pointe donc légèrement vers le haut. Pour les points situés bien au-dessus du\(xy\) plan, la\(z\) composante -est grande, de sorte que le vecteur est presque vertical. La figure\(\PageIndex{6}\) montre ce champ vectoriel.
Figure\(\PageIndex{6}\) : Représentation visuelle d'un champ vectoriel\(\vecs{F}(x,y,z)=⟨1,1,z⟩\).
Champ vectoriel d'esquisse\(\vecs{G}(x,y,z)=⟨2,\,\dfrac{z}{2},\,1⟩\).
- Allusion
-
Substituez suffisamment de points dans le champ vectoriel pour avoir une idée de la forme générale.
- Réponse
Dans l'exemple suivant, nous explorons l'un des cas classiques d'un champ vectoriel tridimensionnel : un champ gravitationnel.
La loi de la gravitation de Newton indique que\(\vecs{F}=−G\dfrac{m_1m_2}{r^2}\hat{\mathbf r}\), où G est la constante gravitationnelle universelle. Il décrit le champ gravitationnel exercé par un objet (objet 1) de masse\(m_1\) situé à l'origine sur un autre objet (objet 2) de masse\(m_2\) situé au point\((x,y,z)\). Le champ\(\vecs{F}\) indique la force gravitationnelle que l'objet 1 exerce sur l'objet 2,\(r\) est la distance entre les deux objets et\(\hat{\mathbf r}\) indique le vecteur unitaire du premier objet au second. Le signe moins indique que la force gravitationnelle s'attire vers l'origine, c'est-à-dire que la force de l'objet 1 est attractive. Esquissez le champ vectoriel associé à cette équation.
Solution
Puisque l'objet 1 est situé à l'origine, la distance entre les objets est donnée par\(r=\sqrt{x^2+y^2+z^2}\). Le vecteur unitaire de l'objet 1 à l'objet 2 est\(\hat{\mathbf r}=\dfrac{⟨x,y,z⟩}{||⟨x,y,z⟩||}\), et donc\(\hat{\mathbf r}=\big\langle\dfrac{x}{r},\dfrac{y}{r},\dfrac{z}{r}\big\rangle\). Par conséquent, le champ vectoriel gravitationnel\(\vecs{F}\) exercé par l'objet 1 sur l'objet 2 est
\[ \vecs{F}=−Gm_1m_2\big\langle\dfrac{x}{r^3},\dfrac{y}{r^3},\dfrac{z}{r^3}\big\rangle. \nonumber \]
Voici un exemple de champ vectoriel radial dans\(ℝ^3\).
La figure\(\PageIndex{7}\) montre à quoi ressemble ce champ gravitationnel pour une masse importante à l'origine. Notez que les magnitudes des vecteurs augmentent à mesure que les vecteurs se rapprochent de l'origine.
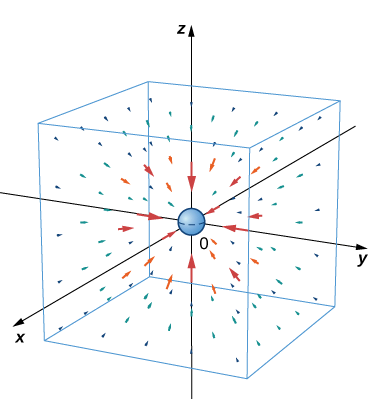
La masse de l'astéroïde 1 est de 750 000 kg et celle de l'astéroïde 2 est de 130 000 kg. Supposons que l'astéroïde 1 est situé à l'origine et que l'astéroïde 2 est situé à\((15,−5,10)\), en unités de 10 à 8 kilomètres de puissance. Étant donné que la constante gravitationnelle universelle est\(G=6.67384×10^{−11}m^3{kg}^{−1}s^{−2}\), trouvez le vecteur de force gravitationnelle que l'astéroïde 1 exerce sur l'astéroïde 2.
- Allusion
-
Suivez l'exemple\(\PageIndex{8}\) et calculez d'abord la distance entre les astéroïdes.
- Réponse
-
\(1.49063×{10}^{−18}\),\(4.96876×{10}^{−19}\),\(9.93752×{10}^{−19}\) N
Champs de gradient (champs conservateurs)
Dans cette section, nous étudions un type spécial de champ vectoriel appelé champ de gradient ou champ conservateur. Ces champs vectoriels sont extrêmement importants en physique car ils peuvent être utilisés pour modéliser des systèmes physiques dans lesquels l'énergie est conservée. Les champs gravitationnels et les champs électriques associés à une charge statique sont des exemples de champs de gradient.
Rappelez-vous que si\(f\) est une fonction (scalaire) de\(x\) et\(y\), alors le gradient de\(f\) est
\[ \text{grad}\, f =\vecs \nabla f(x,y) =f_x(x,y) \hat{\mathbf i} +f_y(x,y) \hat{\mathbf j}. \nonumber \]
Nous pouvons voir dans la forme dans laquelle le dégradé est écrit qu'il\(\vecs \nabla f\) s'agit d'un champ vectoriel\(ℝ^2\). De même, si\(f\) est fonction de\(x\)\(y\), et\(z\), alors le gradient de\(f\) est
\[ \text{grad}\, f =\vecs \nabla f(x,y,z) = f_x(x,y,z) \hat{\mathbf i}+f_y(x,y,z) \hat{\mathbf j}+f_z(x,y,z)\hat{\mathbf k}. \nonumber \]
Le gradient d'une fonction à trois variables est un champ vectoriel dans\(ℝ^3\). Un champ de dégradé est un champ vectoriel qui peut être écrit comme le dégradé d'une fonction, et nous avons la définition suivante.
Un champ vectoriel\(\vecs{F}\) dans\(ℝ^2\) ou dans\(ℝ^3\) est un champ de gradient s'il existe une fonction scalaire\(f\) telle que\(\vecs \nabla f=\vecs{F}\).
Utilisez la technologie pour tracer le champ vectoriel du gradient de\(f(x,y)=x^2y^2\).
Solution
Le gradient de\(f\) est\(\vecs \nabla f(x,y)=⟨2xy^2,\,2x^2y⟩\). Pour esquisser le champ vectoriel, utilisez un système d'algèbre informatique tel que Mathematica. La figure\(\PageIndex{8}\) le montre\(\vecs \nabla f\).
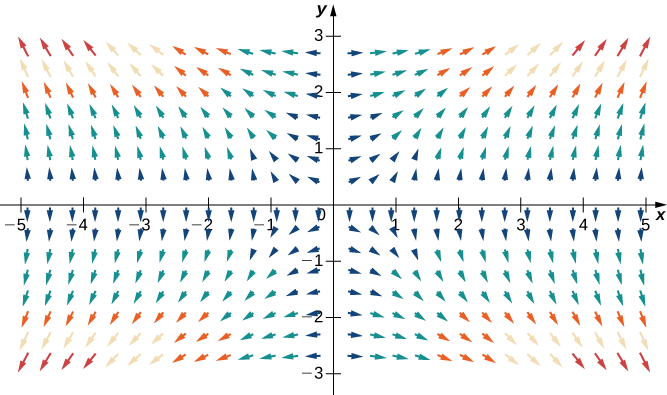
Utilisez la technologie pour tracer le champ vectoriel du gradient de\(f(x,y)=\sin x\cos y\).
- Allusion
-
Trouvez le dégradé de\(f\).
- Réponse
-
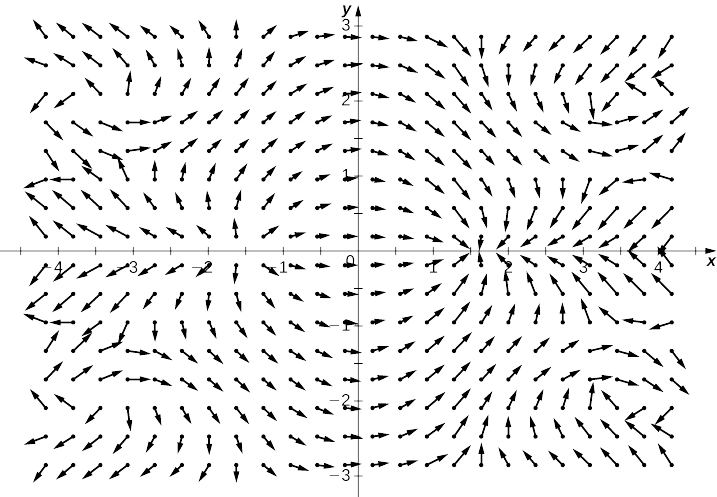
Considérez la fonction\(f(x,y)=x^2y^2\) de l'exemple\(\PageIndex{9}\). La figure\(\PageIndex{9}\) montre les courbes de niveau de cette fonction superposées au champ vectoriel de gradient de la fonction. Les vecteurs de gradient sont perpendiculaires aux courbes de niveau, et leurs magnitudes augmentent à mesure que les courbes de niveau se rapprochent, car des courbes de niveau étroitement groupées indiquent que le graphe est abrupt et que l'amplitude du vecteur de gradient est la plus grande valeur de la dérivée directionnelle. Par conséquent, vous pouvez voir la pente locale d'un graphe en étudiant le champ de gradient de la fonction correspondante.
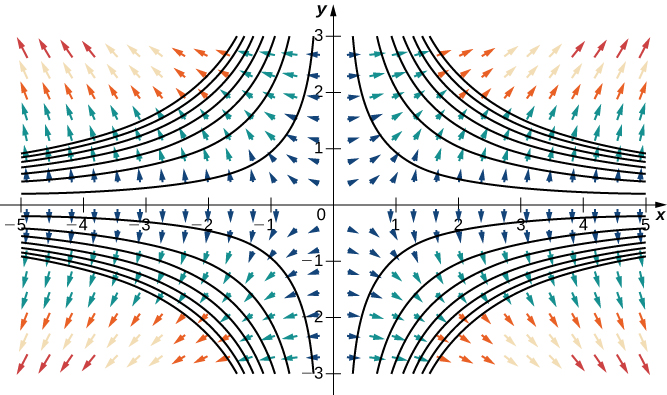
Comme nous l'avons appris précédemment, un champ vectoriel\(\vecs{F}\) est un champ vectoriel conservateur, ou un champ de gradient s'il existe une fonction scalaire\(f\) telle que\(\vecs \nabla f=\vecs{F}\). Dans ce cas,\(f\) on parle de fonction potentielle pour\(\vecs{F}\). Les champs vectoriels conservateurs apparaissent dans de nombreuses applications, notamment en physique. La raison pour laquelle ces champs sont qualifiés de conservateurs est qu'ils modélisent les forces des systèmes physiques dans lesquels l'énergie est conservée. Nous étudions les champs vectoriels conservateurs plus en détail plus loin dans ce chapitre.
Vous remarquerez peut-être que, dans certaines applications, une fonction potentielle\(f\) pour\(\vecs{F}\) est définie à la place comme une fonction telle que\(−\vecs \nabla f=\vecs{F}\). C'est le cas pour certains contextes en physique, par exemple.
Est\(f(x,y,z)=x^2yz−\sin(xy)\) une fonction potentielle pour le champ vectoriel
\(\vecs{F}(x,y,z)=⟨2xyz−y\cos(xy),x^2z−x\cos(xy),x^2y⟩\)?
Solution
Nous devons confirmer si\(\vecs \nabla f=\vecs{F}\). Nous avons
\[ \begin{align*} f_x(x,y) =2xyz−y\cos(xy) \\[4pt] f_y(x,y) =x^2z−x\cos(xy) \\[4pt] f_z(x,y) =x^2y \end{align*}. \nonumber \]
Par conséquent,\(\vecs \nabla f=\vecs{F}\) et\(f\) est une fonction potentielle pour\(\vecs{F}\).
Est-ce\(f(x,y,z)=x^2\cos(yz)+y^2z^2\) qu'une fonction potentielle est pour\(\vecs{F}(x,y,z)=⟨2x\cos(yz),−x^2z \sin(yz)+2yz^2,y^2⟩\) ?
- Allusion
-
Calculez le gradient de\(f\).
- Réponse
-
Non
La vitesse d'un fluide est modélisée par champ\(\vecs v(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\). Vérifiez qu'il\(f(x,y)=\dfrac{x^2y}{2}−\dfrac{y^2}{2}\) s'agit d'une fonction potentielle pour\(\vecs{v}\).
Solution
Pour montrer qu'il\(f\) s'agit d'une fonction potentielle, nous devons la montrer\(\vecs \nabla f=\vecs v\). Notez que\(f_x(x,y)=xy\) et\(f_y(x,y)=\dfrac{x^2}{2}−y\). Par conséquent,\(\vecs \nabla f(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\) et\(f\) est une fonction potentielle pour\(\vecs{v}\) (Figure\(\PageIndex{10}\)).

Vérifiez qu'il\(f(x,y)=x^3y^2+x\) s'agit d'une fonction potentielle pour le champ de vitesse\(\vecs{v}(x,y)=⟨3x^2y^2+1,2x^3y⟩\).
- Allusion
-
Calculez le dégradé.
- Réponse
-
\(\vecs \nabla f(x,y)=\vecs{v}(x,y)\)
S'il s'\(\vecs{F}\)agit d'un champ vectoriel conservateur, il existe au moins une fonction potentielle\(f\) telle que\(\vecs \nabla f=\vecs{F}\). Mais pourrait-il y avoir plus d'une fonction potentielle ? Dans l'affirmative, existe-t-il une relation entre deux fonctions potentielles pour le même champ vectoriel ? Avant de répondre à ces questions, rappelons quelques faits du calcul à variable unique pour guider notre intuition. Rappelons que c'\(k(x)\)est une fonction intégrable,\(k\) elle possède alors une infinité d'antidérivés. De plus, si\(\vecs{F}\) et\(\vecs{G}\) sont tous deux antidérivés de\(k\), alors\(\vecs{F}\) et ne\(\vecs{G}\) diffèrent que par une constante. C'est-à-dire qu'il y en a un\(C\) certain nombre\(\vecs{F}(x)=\vecs{G}(x)+C\).
\(\vecs{F}\)Soyons maintenant un champ vectoriel conservateur et laissez\(f\) et\(g\) soyez des fonctions potentielles pour\(\vecs{F}\). Puisque le gradient est comme un dérivé,\(\vecs{F}\) être conservateur signifie qu'il\(\vecs{F}\) est « intégrable » aux « antidérivés »\(f\) et\(g\). Par conséquent, si l'analogie avec le calcul à variable unique est valide, nous nous attendons à ce qu'il y ait une constante\(C\) telle que\(f(x)=g(x)+C\). Le théorème suivant indique que c'est bien le cas.
Pour énoncer le théorème suivant avec précision, nous devons supposer que le domaine du champ vectoriel est connecté et ouvert. Être connecté signifie s'il\(P_1\)\(P_2\) y a deux points dans le domaine, alors vous pouvez marcher de\(P_1\) à pied\(P_2\) le long d'un chemin qui reste entièrement à l'intérieur du domaine.
\(\vecs{F}\)Soyons un champ vectoriel conservateur sur un domaine ouvert et connecté et laissez\(f\) et\(g\) soyez des fonctions telles que\(\vecs \nabla f=\vecs{F}\) et\(\vecs \nabla g=\vecs{F}\). Ensuite, il existe une constante\(C\) telle que\(f=g+C\).
Puisque\(f\) et\(g\) sont tous deux des fonctions potentielles pour\(\vecs{F}\), alors\(\vecs \nabla (f−g)=\vecs \nabla f−\vecs \nabla g=\vecs{F}−\vecs{F}=\vecs 0\). Nous avons donc\(\vecs \nabla h=\vecs 0\). Nous aimerions montrer que\(h\) c'est une fonction constante.\(h=f−g\)
\(h\)Suppose est fonction de\(x\) et\(y\) (la logique de cette preuve s'étend à n'importe quel nombre de variables indépendantes). Depuis\(\vecs \nabla h=\vecs 0\), nous avons\(h_x(x,y)=0\) et\(h_y(x,y)=0\). L'expression\(h_x(x,y)=0\) implique qu'il\(h\) s'agit d'une fonction constante par rapport à\(x\) — c'est-à-dire\(h(x,y)=k_1(y)\) pour certaines fonctions\(k_1\). De même,\(h_y(x,y)=0\) implique\(h(x,y)=k_2(x)\) pour une certaine fonction\(k_2\). Par conséquent, la fonction ne\(h\) dépend que de\(y\) et ne dépend que de\(x\). Ainsi,\(h(x,y)=C\) pour une certaine constante\(C\) sur le domaine connecté de\(\vecs{F}\). Notez que nous avons vraiment besoin de connectivité à ce stade ; si le domaine de\(\vecs{F}\) venait en deux parties distinctes, alors\(k\) pourrait être une constante\(C_1\) sur une pièce mais pourrait être une constante différente\(C_2\) sur l'autre pièce. Depuis\(f−g=h=C\), nous l'avons\(f=g+C\), comme vous le souhaitez.
\(\square\)
Les champs vectoriels conservateurs possèdent également une propriété spéciale appelée propriété partielle croisée. Cette propriété permet de tester si un champ vectoriel donné est conservateur.
\(\vecs{F}\)Soit un champ vectoriel en deux ou trois dimensions de telle sorte que les fonctions constitutives de\(\vecs{F}\) aient des dérivées partielles mixtes continues du second ordre sur le domaine de\(\vecs{F}\).
S'il s'\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\)agit d'un champ vectoriel conservateur dans\(ℝ^2\), alors
\[\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. \nonumber \]
S'il s'\(\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩\)agit d'un champ vectoriel conservateur dans\({\mathbb{R}}^3\), alors
\[ \begin{align*} \dfrac{\partial P}{\partial y} =\dfrac{\partial Q}{\partial x} \\[4pt] \dfrac{\partial Q}{\partial z} =\dfrac{\partial R}{\partial y} \\[4pt] \dfrac{\partial R}{\partial x} =\dfrac{\partial P}{\partial z}. \end{align*}\]
Puisque\(\vecs{F}\) c'est conservateur, il existe une fonction\(f(x,y)\) telle que\(\vecs \nabla f=\vecs{F}\). Par conséquent, par la définition du gradient,\(f_x=P\) et\(f_y=Q\). Par le théorème de Clairaut\(f_{xy}=f_{yx}\), Mais,\(f_{xy}=P_y\) et\(f_{yx}=Q_{x}\), et donc\(P_y=Q_x\).
\(\square\)
Le théorème de Clairaut fournit une preuve rapide de la propriété partielle croisée des champs vectoriels conservateurs dans\(ℝ^3\), tout comme il l'a fait pour les champs vectoriels dans\(ℝ^2\).
La propriété partielle croisée des champs vectoriels conservateurs montre que la plupart des champs vectoriels ne sont pas conservateurs. La propriété des partiels croisés est difficile à satisfaire en général, de sorte que la plupart des champs vectoriels n'auront pas de partiels croisés égaux.
Montrez que le champ vectoriel de rotation n'\(\vecs{F}(x,y)=⟨y,\,−x⟩\)est pas conservateur.
Solution
Laissez\(P(x,y)=y\) et\(Q(x,y)=−x\). Si\(\vecs{F}\) c'est conservateur, alors les partiels croisés seraient égaux, c'est-à-dire égaux\(Q_x\). Par conséquent,\(P_y\) pour montrer que ce n'\(\vecs{F}\)est pas conservateur, cochez cette case\(P_y≠Q_x\). Depuis\(P_y=1\) et\(Q_x=−1\), le champ vectoriel n'est pas conservateur.
Afficher que le champ vectoriel n'\(\vecs F(x,y)=xy\,\hat{\mathbf i}−x^2y\,\hat{\mathbf j}\)est pas conservateur.
- Allusion
-
Vérifiez les partiels croisés.
- Réponse
-
\(P_y(x,y)=x\)et\(Q_x(x,y)=−2xy\). Puisque\(P_y(x,y) ≠ Q_x(x,y)\), n'\(\vecs F\)est pas conservateur.
Le champ vectoriel est-il\(\vecs{F}(x,y,z)=⟨7,−2,x^3⟩\) conservateur ?
Solution
Laissez\(P(x,y,z)=7\)\(Q(x,y,z)=−2\), et\(R(x,y,z)=x^3\). Si elle\(\vecs{F}\) est conservatrice, les trois équations partielles croisées seront satisfaites, c'est-à-dire que si elle\(\vecs{F}\) est conservatrice, alors\(P_y\) serait égale\(Q_x\),\(Q_z\) serait égale\(R_y\) et\(R_x\) serait égale\(P_z\). Notez que
\[P_y=Q_x=R_y=Q_z=0 \nonumber \]
les deux premières égalités nécessaires sont donc valables. Cependant,\(R_x(x,y,z)=x^3\) et ainsi de\(P_z(x,y,z)=0\) suite\(R_x≠P_z\). Par conséquent, n'\(\vecs{F}\)est pas conservateur.
Le champ vectoriel est-il\(\vecs{G}(x,y,z)=⟨y,\,x,\,xyz⟩\) conservateur ?
- Allusion
-
Vérifiez les partiels croisés.
- Réponse
-
Non
Nous concluons cette section par un mot d'avertissement : La propriété partielle croisée des champs vectoriels conservateurs indique que si elle\(\vecs{F}\) est conservatrice, elle\(\vecs{F}\) possède alors la propriété partielle croisée. Le théorème ne dit pas que, s'il\(\vecs{F}\) possède la propriété partielle croisée, il\(\vecs{F}\) est conservateur (l'inverse d'une implication n'est pas logiquement équivalent à l'implication initiale). En d'autres termes, la propriété partielle croisée des champs vectoriels conservateurs ne peut qu'aider à déterminer qu'un champ n'est pas conservateur ; elle ne vous permet pas de conclure qu'un champ vectoriel est conservateur.
Par exemple, considérez le champ vectoriel\(\vecs{F}(x,y)=⟨x^2y,\dfrac{x^3}{3}⟩\). Ce champ possède la propriété partielle croisée, il est donc naturel d'essayer d'utiliser la propriété transversale des champs vectoriels conservateurs pour conclure que ce champ vectoriel est conservateur. Cependant, il s'agit d'une mauvaise application du théorème. Nous apprendrons plus tard comment conclure que\(\vecs F\) c'est conservateur.
Concepts clés
- Un champ vectoriel attribue un vecteur\(\vecs{F}(x,y)\) à chaque point\((x,y)\) d'un sous-ensemble\(D\) de\(ℝ^2\) ou\(ℝ^3\). \(\vecs{F}(x,y,z)\)à chaque point\((x,y,z)\) d'un sous-ensemble\(D\) de\(ℝ^3\).
- Les champs vectoriels peuvent décrire la distribution de quantités vectorielles telles que les forces ou les vitesses sur une région du plan ou de l'espace. Ils sont couramment utilisés dans des domaines tels que la physique, l'ingénierie, la météorologie et l'océanographie.
- Nous pouvons esquisser un champ de vecteurs en examinant son équation de définition pour déterminer les magnitudes relatives à divers emplacements, puis en dessinant suffisamment de vecteurs pour déterminer un motif.
- Un champ vectoriel\(\vecs{F}\) est dit conservateur s'il existe une fonction scalaire\(f\) telle que\(\vecs \nabla f=\vecs{F}\).
Équations clés
- Champ vectoriel dans\(ℝ^2\)
\(\vecs{F}(x,y)=⟨P(x,y),\,Q(x,y)⟩\)
ou
\(\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}\) - Champ vectoriel dans\(ℝ^3\)
\(\vecs{F}(x,y,z)=⟨P(x,y,z),\,Q(x,y,z),\,R(x,y,z)⟩\)
ou
\(\vecs{F}(x,y,z)=P(x,y,z) \,\hat{\mathbf i} +Q(x,y,z) \,\hat{\mathbf j}+R(x,y,z) \,\hat{\mathbf k}\)
Lexique
- domaine conservateur
- un champ vectoriel pour lequel il existe une fonction scalaire\(f\) telle que\(\vecs ∇f=\vecs{F}\)
- champ dégradé
- un champ vectoriel\(\vecs{F}\) pour lequel il existe une fonction scalaire\(f\) telle que\(\vecs ∇f=\vecs{F}\), en d'autres termes, un champ vectoriel qui est le gradient d'une fonction ; de tels champs vectoriels sont également appelés conservateurs
- fonction potentielle
- une fonction scalaire\(f\) telle que\(\vecs ∇f=\vecs{F}\)
- champ radial
- un champ vectoriel dans lequel tous les vecteurs pointent directement vers ou loin de l'origine ; l'amplitude de tout vecteur dépend uniquement de sa distance par rapport à l'origine
- champ de rotation
- un champ vectoriel dans lequel le vecteur au point\((x,y)\) est tangent à un cercle de rayon\(r=\sqrt{x^2+y^2}\) ; dans un champ de rotation, tous les vecteurs circulent dans le sens des aiguilles d'une montre ou dans le sens antihoraire, et l'amplitude d'un vecteur dépend uniquement de sa distance par rapport à l'origine
- champ vectoriel unitaire
- un champ de vecteurs dans lequel la magnitude de chaque vecteur est de 1
- champ vectoriel
- mesurée en\(ℝ^2\), une affectation d'un vecteur\(\vecs{F}(x,y)\) à chaque point\((x,y)\) d'un sous-ensemble\(D\) de\(ℝ^2\) ; dans\(ℝ^3\), une affectation d'un vecteur\(\vecs{F}(x,y,z)\) à chaque point\((x,y,z)\) d'un sous-ensemble\(D\) de\(ℝ^3\)


