16.4 : Théorème de Green
- Page ID
- 197897
- Appliquez la forme circulatoire du théorème de Green.
- Appliquez la forme de flux du théorème de Green.
- Calculez la circulation et le flux sur des régions plus générales.
Dans cette section, nous examinons le théorème de Green, qui est une extension du théorème fondamental du calcul à deux dimensions. Le théorème de Green a deux formes : une forme de circulation et une forme de flux, qui nécessitent toutes deux qu'une région\(D\) de la double intégrale soit simplement connectée. Cependant, nous étendrons le théorème de Green aux régions qui ne sont pas simplement connectées.
En termes simples, le théorème de Green met en relation une droite intégrale autour d'une courbe plane simplement fermée\(C\) et une double intégrale sur la région délimitée par\(C\). Le théorème est utile car il nous permet de traduire des intégrales linéaires difficiles en intégrales doubles plus simples, ou des intégrales doubles difficiles en intégrales linéaires plus simples.
Étendre le théorème fondamental du calcul
Rappelons que le théorème fondamental du calcul dit que
\[\int_a^b F′(x)\,dx=F(b)−F(a). \nonumber \]
En tant qu'énoncé géométrique, cette équation indique que l'intégrale sur la région située sous le graphique\(F′(x)\) et au-dessus\([a,b]\) du segment de droite dépend uniquement de la valeur des\(F\) extrémités\(a\) et\(b\) de ce segment. Puisque les nombres\(a\) et\(b\) sont la limite du segment de ligne\([a,b]\), le théorème indique que nous pouvons calculer l'intégrale sur la\(\int_a^b F′(x)\,dx\) base des informations concernant la limite du segment de ligne\([a,b]\) (Figure\(\PageIndex{1}\)). La même idée est vraie pour le théorème fondamental des intégrales linéaires :
\[\int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]
Lorsque nous avons une fonction potentielle (une « antidérivée »), nous pouvons calculer l'intégrale de la droite en nous basant uniquement sur les informations concernant la limite de la courbe\(C\).
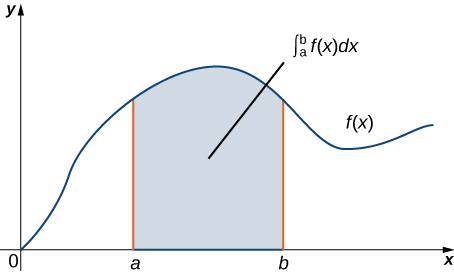
Le théorème de Green reprend cette idée et l'étend au calcul d'intégrales doubles. Le théorème de Green indique que nous pouvons calculer une double intégrale sur la région en nous\(D\) basant uniquement sur les informations concernant la limite de\(D\). Le théorème de Green indique également que nous pouvons calculer une intégrale droite sur une simple courbe fermée en nous\(C\) basant uniquement sur les informations concernant la région qui l'\(C\)entoure. En particulier, le théorème de Green relie une double intégrale au-dessus de la région\(D\) à une droite intégrale autour de la limite de\(D\).
Forme de circulation du théorème de Green
La première forme du théorème de Green que nous examinons est la forme de circulation. Cette forme du théorème met en relation l'intégrale de la droite vectorielle sur une courbe plane fermée simple\(C\) à une intégrale double sur la région délimitée par\(C\). Par conséquent, la circulation d'un champ vectoriel le long d'une simple courbe fermée peut être transformée en une double intégrale et vice versa.
\(D\)Soit une région ouverte et simplement connectée avec une courbe limite\(C\) qui est une courbe fermée simple et lisse par morceaux orientée dans le sens antihoraire (Figure\(\PageIndex{1}\)). \(\vecs F=⟨P,Q⟩\)Soit un champ vectoriel avec des fonctions de composants sur lesquelles des dérivées partielles continues sont activées\(D\). Ensuite,
\[ \begin{align} \oint_C \vecs F·d\vecs r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align} \nonumber \]
Notez que le théorème de Green ne peut être utilisé que pour un champ vectoriel bidimensionnel\(\vecs F\). S'il s'\(\vecs F\)agit d'un champ tridimensionnel, le théorème de Green ne s'applique pas. Depuis
\[\displaystyle \int_C P\,dx+Q\,dy=\int_C \vecs F·\vecs T\,ds \nonumber \]
cette version du théorème de Green est parfois appelée forme tangentielle du théorème de Green.
La preuve du théorème de Green est assez technique et dépasse le cadre de ce texte. Nous examinons ici une preuve du théorème dans le cas particulier qu'\(D\)est un rectangle. Pour l'instant, notez que nous pouvons rapidement confirmer que le théorème est vrai pour le cas particulier où\(\vecs F=⟨P,Q⟩\) il est conservateur. Dans ce cas,
\[\oint_C P\,dx+Q\,dy=0 \nonumber \]
car la circulation est nulle dans les champs vectoriels conservateurs. \(\vecs F\)satisfait à la condition de partialité croisée, donc\(P_y=Q_x\). Par conséquent,
\[\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy \nonumber \]
ce qui confirme le théorème de Green dans le cas de champs vectoriels conservateurs.
Prouvons maintenant que la forme de circulation du théorème de Green est vraie lorsque la région\(D\) est un rectangle. \(D\)Soit le rectangle\([a,b]×[c,d]\) orienté dans le sens antihoraire. Ensuite, la limite\(C\) de\(D\) se compose de quatre pièces lisses par morceaux\(C_1\)\(C_2\),\(C_3\), et\(C_4\) (Figure\(\PageIndex{3}\)). Nous paramétrons chaque côté de la\(D\) manière suivante :
\(C_1: \vecs r_1(t)=⟨t,c⟩\),\(a≤t≤b\)
\(C_2: \vecs r_2(t)=⟨b,t⟩\),\(c≤t≤d\)
\(−C_3: \vecs r_3(t)=⟨t,d⟩\),\(a≤t≤b\)
\(−C_4: \vecs r_4(t)=⟨a,t⟩\),\(c≤t≤d\).
Ensuite,
\[\begin{align*} \int_C \vecs F·d \vecs r &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r+\int_{C_3} \vecs F·d \vecs r+\int_{C_4} \vecs F·d \vecs r \\[4pt] &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r−\int_{−C_3} \vecs F·d \vecs r−\int_{−C_4} \vecs F·d \vecs r \\[4pt] &=\int_a^b \vecs F( \vecs r_1(t))· \vecs r_1'(t)\,dt+\int_c^d \vecs F( \vecs r_2(t))· \vecs r_2'(t)\,dt−\int_a^b \vecs F( \vecs r_3(t))· \vecs r_3'(t)\,dt−\int_c^d \vecs F( \vecs r_4(t))·\vecs r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}\]
Selon le théorème fondamental du calcul,
\[P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber \]
et
\[Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber \]
Par conséquent,
\[−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber \]
Mais
\[\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}\]
Par conséquent,\(\displaystyle \int_C \vecs F\cdot d\vecs r=\iint_D(Q_x−P_y)\,dA\) et nous avons prouvé le théorème de Green dans le cas d'un rectangle.
\(\square\)
Pour prouver le théorème de Green sur une région générale\(D\), nous pouvons le décomposer\(D\) en de nombreux petits rectangles et utiliser la preuve que le théorème fonctionne sur des rectangles. Les détails sont toutefois techniques et dépassent le cadre de ce texte.
Calculer l'intégrale de la ligne
\[\oint_C x^2ydx+(y−3)dy, \nonumber \]
où\(C\) est un rectangle avec des sommets\((1,1)\),\((4,1)\)\((4,5)\), et\((1,5)\) orienté dans le sens antihoraire.
Solution
Laissez\( \vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩\). Ensuite,\(Q_x(x,y)=0\) et\(P_y(x,y)=x^2\). Par conséquent,\(Q_x−P_y=−x^2\).
\(D\)Soit la région rectangulaire délimitée par\(C\) (Figure\(\PageIndex{4}\)). Selon le théorème de Green,
\[\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}\]

Analyse
Si nous devions évaluer cette intégrale linéaire sans utiliser le théorème de Green, nous devrions paramétrer chaque côté du rectangle, diviser l'intégrale de la ligne en quatre intégrales linéaires distinctes et utiliser les méthodes de la section intitulée Intégrales de ligne pour évaluer chaque intégrale. De plus, comme le champ vectoriel ici n'est pas conservateur, nous ne pouvons pas appliquer le théorème fondamental pour les intégrales linéaires. Le théorème de Green simplifie considérablement le calcul.
Calculer le travail effectué sur une particule par champ de force
\[\vecs F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber \]
car la particule traverse un cercle\(x^2+y^2=4\) exactement une fois dans le sens antihoraire, en commençant et en finissant au point\((2,0)\).
Solution
\(C\)Soit le cercle et\(D\) soit le disque entouré de celui-ci\(C\). Le travail effectué sur la particule est
\[W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber \]
Comme pour Example\(\PageIndex{1}\), cette intégrale peut être calculée à l'aide des outils que nous avons appris, mais il est plus facile d'utiliser la double intégrale donnée par le théorème de Green (Figure\(\PageIndex{5}\)).
Laissez\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩\). Ensuite,\(Q_x=−1\) et\(P_y=1\). Par conséquent,\(Q_x−P_y=−2\).
Selon le théorème de Green,
\[\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}\]
Utiliser le théorème de Green pour calculer l'intégrale de la droite
\[\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber \]
où\(C\) est un triangle droit avec des sommets\((−1,2)\) et\((4,5)\) orienté dans le sens antihoraire.\((4,2)\)
- Allusion
-
Transformez l'intégrale linéaire en une intégrale double.
- Réponse
-
\(\dfrac{45}{2}\)
Dans les deux exemples précédents, l'intégrale double du théorème de Green était plus facile à calculer que l'intégrale droite. Nous avons donc utilisé le théorème pour calculer l'intégrale droite. Dans l'exemple suivant, l'intégrale double est plus difficile à calculer que l'intégrale droite. Nous utilisons donc le théorème de Green pour traduire une intégrale double en une intégrale droite.
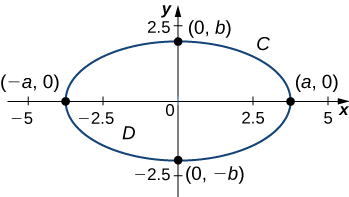
Calculez la surface délimitée par une ellipse\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) (Figure\(\PageIndex{6}\)).
Solution
\(C\)Soit l'ellipse et\(D\) soit la région délimitée par\(C\). Rappelons que l'ellipse\(C\) peut être paramétrée par
- \(x=a\cos t\),
- \(y=b \sin t\),
- \(0≤t≤2\pi\).
Le calcul de l'aire de\(D\) est équivalent au calcul de la double intégrale\(\iint_D \,dA\). Pour calculer cette intégrale sans le théorème de Green, il faudrait la\(D\) diviser en deux régions : la région située au-dessus de l'axe x et la région inférieure. L'aire de l'ellipse est
\[\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber \]
Ces deux intégrales ne sont pas simples à calculer (bien que lorsque nous connaissons la valeur de la première intégrale, nous connaissons la valeur de la seconde par symétrie). Au lieu d'essayer de les calculer, nous utilisons le théorème de Green pour les\(\iint_D \,dA\) transformer en une droite intégrale autour de la limite\(C\).
Considérez le champ vectoriel
\[F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber \]
Ensuite\(P_y=−\dfrac{1}{2}\),\(Q_x=\dfrac{1}{2}\) et donc\(Q_x−P_y=1\). Remarquez\(\vecs F\) que vous avez choisi de posséder la propriété qui\(Q_x−P_y=1\). Puisque c'est le cas, le théorème de Green transforme l'intégrale droite de\(\vecs F\) over\(C\) en l'intégrale double de 1 over\(D\).
Selon le théorème de Green,
\[\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \vecs F\cdot d\vecs r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}\]
Par conséquent, l'aire de l'ellipse est\(\pi ab\;\text{units}^2\).
Dans l'exemple\(\PageIndex{3}\), nous avons utilisé un champ vectoriel\(\vecs F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\) pour trouver l'aire de n'importe quelle ellipse. La logique de l'exemple précédent peut être étendue pour dériver une formule pour la superficie de n'importe quelle région\(D\). \(D\)Soit n'importe quelle région dont la limite est une simple courbe fermée\(C\) orientée dans le sens antihoraire. Si\(F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\), alors\(Q_x−P_y=1\). Par conséquent, selon la même logique que dans l'exemple\(\PageIndex{3}\),
\[ \text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea} \]
Il convient de noter que s'il s'\(F=⟨P,Q⟩\)agit d'un champ vectoriel\(Q_x−P_y=1\), la logique du paragraphe précédent fonctionne. Donc. L'équation \ ref {greenarea} n'est pas la seule équation qui utilise les partiels mixtes d'un champ vectoriel pour obtenir l'aire d'une région.
Trouvez l'aire de la région délimitée par la courbe avec paramétrage\(r(t)=⟨\sin t\cos t,\sin t⟩\),\(0≤t≤\pi\).
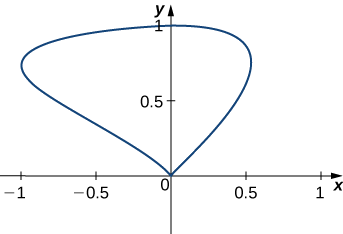
- Allusion
-
Utilisez l'équation \ ref {greenarea}.
- Réponse
-
\(\dfrac{4}{3}\)
Forme de flux du théorème de Green
La forme de circulation du théorème de Green relie une double intégrale sur une région\(D\) à une intégrale linéaire\(\oint_C \vecs F·\vecs Tds\), où\(C\) est la limite de\(D\). La forme de flux du théorème de Green relie une région\(D\) à double intégrale au flux transfrontalier\(C\). Le flux d'un fluide sur une courbe peut être difficile à calculer à l'aide de l'intégrale de la ligne de flux. Cette forme de théorème de Green nous permet de traduire une intégrale de flux difficile en une intégrale double qui est souvent plus facile à calculer.
\(D\)Soit une région ouverte et simplement connectée avec une courbe limite\(C\) qui est une courbe fermée simple et lisse par morceaux orientée dans le sens antihoraire (Figure\(\PageIndex{7}\)). \(\vecs F=⟨P,Q⟩\)Soit un champ vectoriel avec des fonctions composantes qui ont des dérivées partielles continues sur une région ouverte contenant\(D\). Ensuite,
\[\oint_C \vecs F·\vecs N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN} \]
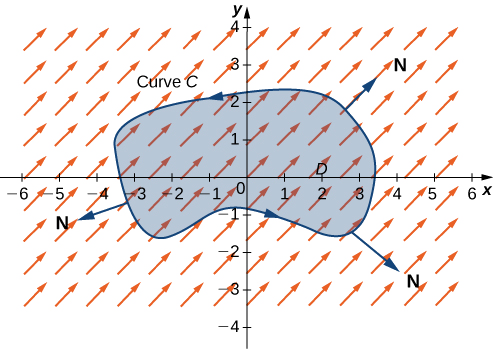
Comme cette forme du théorème de Green contient un vecteur normal unitaire\(\vecs N\), elle est parfois appelée forme normale du théorème de Green.
Souvenez-vous que\(\displaystyle \oint_C \vecs F·\vecs N\,ds=\oint_C −Q\,dx+P\,dy\). Laissez\(M=−Q\) et\(N=P\). Selon la forme circulatoire du théorème de Green,
\[\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}\]
\(\square\)
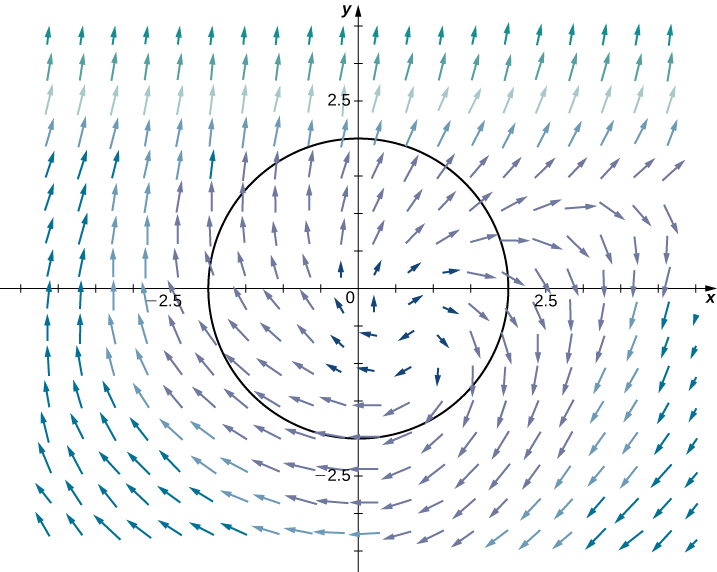
\(C\)Soit un cercle de rayon\(r\) centré sur l'origine (Figure\(\PageIndex{8}\)) et laisse\(\vecs F(x,y)=⟨x,y⟩\). Calculez le flux traversant\(C\).

Solution
\(D\)Soit le disque inclus dans\(C\). Le flux à travers\(C\) est\(\displaystyle \oint_C \vecs F·\vecs N\,ds\). Nous pourrions évaluer cette intégrale à l'aide des outils que nous avons appris, mais le théorème de Green rend le calcul beaucoup plus simple. Laissez\(P(x,y)=x\) et\(Q(x,y)=y\) faites cela\(\vecs F=⟨P,Q⟩\). Notez cela\(P_x=1=Q_y\), et donc\(P_x+Q_y=2\). Selon le théorème de Green,
\[\int_C \vecs F\cdot\vecs N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber \]
Puisque\(\displaystyle \iint_D \,dA\) c'est l'aire du cercle,\(\displaystyle \iint_D \,dA=\pi r^2\). Par conséquent, le flux à travers\(C\) est\(2\pi r^2\).
\(S\)Soit le triangle avec des sommets\((0,0)\)\((1,0)\), et\((0,3)\) orienté dans le sens des aiguilles d'une montre (Figure\(\PageIndex{9}\)). Calculez le flux de\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩\) croix\(S\).
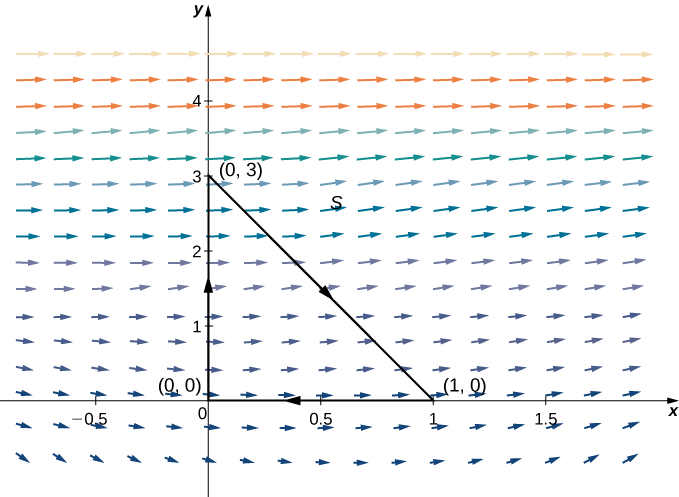
Solution
Pour calculer le flux sans le théorème de Green, il faudrait diviser l'intégrale du flux en trois intégrales linéaires, une intégrale pour chaque côté du triangle. Il est beaucoup plus simple d'utiliser le théorème de Green pour traduire l'intégrale de la ligne de flux en une seule intégrale double.
\(D\)Soyons la région qui l'entoure\(S\). Notez que\(P_x=2x\) et\(Q_y=1\), par conséquent,\(P_x+Q_y=2x+1\). Le théorème de Green ne s'applique qu'aux courbes fermées simples orientées dans le sens antihoraire, mais nous pouvons toujours appliquer le théorème car\(\displaystyle \oint_C \vecs F·\vecs N\,ds=−\oint_{−S} \vecs F·\vecs N\,ds\) et\(−S\) est orienté dans le sens antihoraire. Selon le théorème de Green, le flux est
\[\begin{align*} \oint_C \vecs F·\vecs N\,ds &= \oint_{−S} \vecs F·\vecs N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}\]
Notez que le bord supérieur du triangle est la ligne\(y=−3x+3\). Par conséquent, dans la double intégrale itérée, les\(y\) valeurs -vont de\(y=0\) à\(y=−3x+3\), et nous avons
\[\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}\]
Calculez le flux de\(\vecs F(x,y)=⟨x^3,y^3⟩\) à travers un cercle unitaire orienté dans le sens antihoraire.
- Allusion
-
Appliquez le théorème de Green et utilisez les coordonnées polaires.
- Réponse
-
\(\dfrac{3\pi}{2}\)
L'eau provient d'une source située à l'origine. La vitesse de l'eau est modélisée par champ vectoriel\(\vecs v(x,y)=⟨5x+y,x+3y⟩\) m/sec. Déterminez la quantité d'eau par seconde qui s'écoule à travers le rectangle dont les sommets\((−1,−2)\)\((1,−2)\),\((1,3)\)\((−1,3)\), et sont orientés dans le sens antihoraire (Figure\(\PageIndex{10}\)).

Solution
\(C\)Représentent le rectangle donné et\(D\) soient la région rectangulaire délimitée par\(C\). Pour déterminer la quantité d'eau qui s'écoule\(C\), nous calculons le flux\(\int_C \vecs v\cdot d\vecs r\). Laissez\(P(x,y)=5x+y\) et\(Q(x,y)=x+3y\) faites cela\(\vecs v=⟨P,Q⟩\). Ensuite,\(P_x=5\) et\(Q_y=3\). Selon le théorème de Green,
\[\begin{align*} \int_C \vecs v\cdot d\vecs r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}\]
Le flux d'eau est donc de 80 m 2 /sec.
N'oubliez pas que si le champ vectoriel\(\vecs F\) est conservateur, cela\(\vecs F\) ne fonctionne pas autour des courbes fermées, c'est-à-dire que la circulation\(\vecs F\) autour d'une courbe fermée est nulle. En fait, si le domaine de\(\vecs F\) est simplement connecté, alors\(\vecs F\) est conservateur si et seulement si la circulation\(\vecs F\) autour d'une courbe fermée est nulle. Si nous remplaçons « circulation de\(\vecs F\) » par « flux de »\(\vecs F\), nous obtenons la définition d'un champ vectoriel sans source. Les instructions suivantes sont toutes des manières équivalentes de définir un champ sans source\(\vecs F=⟨P,Q⟩\) sur un domaine simplement connecté (notez les similitudes avec les propriétés des champs vectoriels conservateurs) :
- Le flux\( \displaystyle \oint_C \vecs F·\vecs N\,ds\) sur toute courbe fermée\(C\) est nul.
- Si\(C_1\) et\(C_2\) sont des courbes du domaine de\(\vecs F\) ayant les mêmes points de départ et de fin, alors\(\displaystyle \int_{C_1} \vecs F·\vecs N\,ds=\int_{C_2} \vecs F·\vecs N\,ds\). En d'autres termes, le flux est indépendant du trajet.
- Il existe une fonction de diffusion\(g(x,y)\) pour\(\vecs F\). Une fonction de flux pour\(\vecs F=⟨P,Q⟩\) est une fonction g telle que\(P=g_y\) et\(Q=−g_x\). Géométriquement,\(\vecs F=\langle a,b\rangle\) est tangente à la courbe de niveau de\(g\) at\((a,b)\). Puisque le gradient de\(g\) est perpendiculaire à la courbe de niveau de\(g\) at\((a,b)\), la fonction de flux\(g\) possède la propriété\(\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0\) de n'importe\((a,b)\) quel point du domaine de\(g\). (Les fonctions de flux jouent le même rôle pour les champs sans source que les fonctions potentielles jouent pour les champs conservateurs.)
- \(P_x+Q_y=0\)
Vérifiez que le champ vectoriel de rotation\(\vecs F(x,y)=⟨y,−x⟩\) est exempt de source et recherchez une fonction de flux pour\(\vecs F\).
Solution
Notez que le domaine de\(\vecs F\) est all of\(ℝ^2\), qui est simplement connecté. Par conséquent, pour montrer qu'il n'\(\vecs F\)y a aucune source, nous pouvons montrer que n'importe lequel des éléments 1 à 4 de la liste précédente est vrai. Dans cet exemple, nous montrons que l'élément 4 est vrai. Laissez\(P(x,y)=y\) et\(Q(x,y)=−x\). Alors\(P_x+0=Q_y\), et donc\(P_x+Q_y=0\). Ainsi,\(\vecs F\) est sans source.
Pour rechercher une fonction de flux pour\(\vecs F\), procédez de la même manière que pour rechercher une fonction potentielle pour un champ conservateur. \(g\)Soit une fonction de flux pour\(\vecs F\). Ensuite\(g_y=y\), ce qui implique que
\(g(x,y)=\dfrac{y^2}{2}+h(x)\).
Depuis\(−g_x=Q=−x\), nous avons\(h′(x)=x\). Par conséquent,
\(h(x)=\dfrac{x^2}{2}+C\).
Laisser\(C=0\) donne une fonction de flux
\(g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}\).
Pour confirmer qu'il\(g\) s'agit d'une fonction de flux pour\(\vecs F\), notez que\(g_y=y=P\) et\(−g_x=−x=Q\).
Notez que le champ vectoriel de rotation sans source\(\vecs F(x,y)=⟨y,−x⟩\) est perpendiculaire au champ vectoriel radial conservateur\(\vecs \nabla g=⟨x,y⟩\) (Figure\(\PageIndex{11}\)).
Trouvez une fonction de flux pour le champ vectoriel\(\vecs F(x,y)=⟨x \sin y,\cos y⟩\).
- Allusion
-
Suivez le schéma fourni dans l'exemple précédent.
- Réponse
-
\(g(x,y)=−x\cos y\)
Les champs vectoriels qui sont à la fois conservateurs et exempts de source sont des champs vectoriels importants. Une caractéristique importante des champs vectoriels conservateurs et exempts de source sur un domaine simplement connecté est que toute fonction potentielle\(f\) d'un tel champ satisfait à l'équation de Laplace\(f_{xx}+f_{yy}=0\). L'équation de Laplace est fondamentale dans le domaine des équations aux dérivées partielles car elle modélise des phénomènes tels que les potentiels gravitationnel et magnétique dans l'espace et le potentiel de vitesse d'un fluide idéal. Une fonction qui satisfait l'équation de Laplace est appelée fonction harmonique. Par conséquent, toute fonction potentielle d'un champ vectoriel conservateur et sans source est harmonique.
Pour voir que toute fonction potentielle d'un champ vectoriel conservateur et exempt de source sur un domaine simplement connecté est harmonique,\(f\) supposons une telle fonction potentielle du champ vectoriel\(\vecs F=⟨P,Q⟩\). Alors,\(f_x=P\) et\(f_x=Q\) parce que\(\vecs \nabla f=\vecs F\). Donc,\(f_{xx}=P_x\) et\(f_{yy}=Q_y\). Puisque\(\vecs F\) est sans source\(f_{xx}+f_{yy}=P_x+Q_y=0\), et nous avons cela qui\(f\) est harmonique.
Pour le champ vectoriel\(\vecs F(x,y)=⟨e^x\sin y,e^x\cos y⟩\), vérifiez que le champ est à la fois conservateur et exempt de source, trouvez une fonction potentielle pour\(\vecs F\) et vérifiez que la fonction potentielle est harmonique.
Solution
Laissez\(P(x,y)=e^x\sin y\) et\(Q(x,y)=e^x \cos y\). Notez que le domaine de\(\vecs F\) est entièrement composé de deux espaces, qui sont simplement connectés. Par conséquent, nous pouvons vérifier les partiels croisés de\(\vecs F\) pour déterminer s'il\(\vecs F\) est conservateur. Notez qu'il\(P_y=e^x \cos y=Q_x\) en\(\vecs F\) va de même pour la prudence. Depuis\(P_x=e^x \sin y\) et\(Q_y=e^x \sin y\),\(P_x+Q_y=0\) et le champ est libre de source.
Pour trouver une fonction potentielle pour\(\vecs F\),\(f\) soit une fonction potentielle. Alors\(\vecs \nabla f=\vecs F\), donc\(f_x(x,y)=e^x \sin y\). L'intégration de cette équation par rapport à x donne\(f(x,y)=e^x \sin y+h(y)\). Depuis\(f_y(x,y)=e^x \cos y\), différencier\(f\) par rapport à y donne\(e^x\cos y=e^x\cos y+h′(y)\). Par conséquent, nous pouvons prendre\(h(y)=0\), et\(f(x,y)=e^x\sin y\) est une fonction potentielle pour\(f\).
Pour vérifier qu'il\(f\) s'agit d'une fonction harmonique, notez que\(f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y\) et
\(f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y\). Donc\(f_{xx}+f_{yy}=0\), et\(f\) satisfait l'équation de Laplace.
La fonction est-elle\(f(x,y)=e^{x+5y}\) harmonique ?
- Allusion
-
Déterminez si la fonction satisfait l'équation de Laplace.
- Réponse
-
Non
Théorème de Green sur les régions générales
Le théorème de Green, tel qu'il est indiqué, ne s'applique qu'aux régions simplement connectées, c'est-à-dire que le théorème de Green tel qu'il est indiqué jusqu'à présent ne peut pas gérer les régions présentant des trous. Ici, nous étendons le théorème de Green afin qu'il fonctionne sur des régions comportant un nombre limité de trous (Figure\(\PageIndex{12}\)).
Avant de discuter des extensions du théorème de Green, nous devons passer en revue la terminologie concernant les limites d'une région. Soyons\(D\) une région et\(C\) soyons une composante de la limite de\(D\). Nous disons que\(C\) c'est orienté positivement si, lorsque nous marchons\(C\) dans le sens de l'orientation, la région\(D\) se trouve toujours sur notre gauche. Par conséquent, l'orientation dans le sens antihoraire de la limite d'un disque est une orientation positive, par exemple. \(C\)La courbe est orientée négativement si, lorsque nous marchons\(C\) dans le sens de l'orientation, la région\(D\) est toujours sur notre droite. L'orientation dans le sens des aiguilles d'une montre de la limite d'un disque est une orientation négative, par exemple.
\(D\)Soit une région avec un nombre fini de trous (donc\(D\) un nombre infini de courbes limites) et indiquez la limite de\(D\) par\(\partial D\) (Figure\(\PageIndex{13}\)). Pour étendre le théorème de Green afin qu'il puisse le gérer\(D\), nous divisons la région\(D\) en deux régions,\(D_1\) et\(D_2\) (avec des limites respectives\(\partial D_1\) et\(\partial D_2\)), de telle sorte qu'il\(D=D_1\cup D_2\) n'y\(D_2\) ait\(D_1\) ni trous ni trous (Figure\(\PageIndex{13}\)).
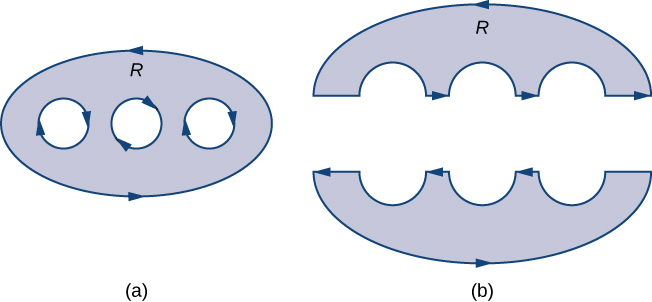
Supposons que la limite de\(D\) soit orientée comme sur la figure, les trous intérieurs étant orientés négativement et la limite extérieure étant orientés positivement. La limite de chaque région\(D_2\) est simplement connectée\(D_1\) et orientée positivement. S'il s'\(\vecs F\)agit d'un champ vectoriel défini sur\(D\), alors le théorème de Green dit que
\[\begin{align} \oint_{\partial D} \vecs F·d\vecs{r} &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align} \nonumber \]
Par conséquent, le théorème de Green fonctionne toujours sur une région présentant des trous.
Pour voir comment cela fonctionne dans la pratique, considérez l'espace annulaire\(D\) dans la figure\(\PageIndex{14}\) et supposons qu'il\(F=⟨P,Q⟩\) s'agit d'un champ vectoriel défini sur cet anneau. \(D\)La région possède un trou, elle n'est donc pas simplement connectée. Orientez le cercle extérieur de l'anneau dans le sens antihoraire et le cercle intérieur dans le sens des aiguilles d'une montre (Figure\(\PageIndex{14}\)) de sorte que\(D_2\), lorsque nous divisons la région en\(D_1\) et, nous puissions garder la région sur notre gauche lorsque nous marchons le long d'un chemin qui traverse la limite. \(D_1\)Soit la moitié supérieure de l'anneau et\(D_2\) la moitié inférieure. Aucune de ces régions ne présente de trous, nous avons donc\(D\) divisé en deux régions simplement connectées.
Nous étiquetons chaque élément de ces nouvelles limites comme\(P_i\) pour certaines\(i\), comme dans la Figure\(\PageIndex{14}\). Si nous commençons à la limite orientée\(P\) et que nous la suivons, le premier segment est\(P_1\)\(P_2\), alors\(P_3\), et\(P_4\). Maintenant, nous avons traversé\(D_1\) et sommes revenus à\(P\). Ensuite, nous\(P\) recommençons et traversons\(D_2\). Puisque la première partie de la frontière est la même que\(P_4\) dans\(D_1\), mais orientée dans la direction opposée, la première partie\(D_2\) est\(−P_4\). Ensuite, nous l'avons fait\(P_5\), puis\(−P_2\), et enfin\(P_6\).
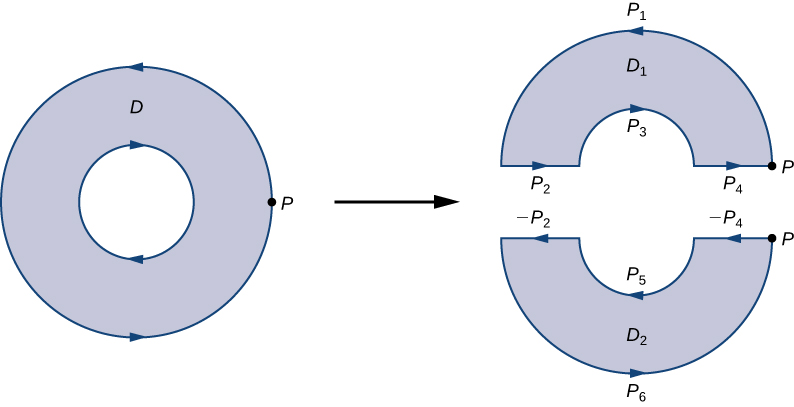
La figure\(\PageIndex{14}\) montre un chemin qui traverse la limite de\(D\). Notez que ce chemin traverse la limite de la région\(D_1\), revient au point de départ, puis traverse la limite de la région\(D_2\). De plus, lorsque nous marchons sur le chemin, la région se trouve toujours sur notre gauche. Notez que cette traversée des\(P_i\) chemins couvre toute la limite de la région\(D\). Si nous n'avions franchi qu'une partie de la limite de\(D\), nous ne pouvons pas appliquer le théorème de Green à\(D\).
La limite de la moitié supérieure de l'anneau est donc\(P_1\cup P_2\cup P_3\cup P_4\) et la limite de la moitié inférieure de l'anneau est\(−P_4\cup P_5\cup −P_2\cup P_6\). Ensuite, le théorème de Green implique
\[\begin{align} \oint_{\partial D}\vecs F·d\vecs{r} &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{−P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align} \nonumber \]
Nous arrivons donc à l'équation contenue dans le théorème de Green, à savoir,
\[\oint_{\partial D}\vecs F·d\vecs{r}=\iint_D (Q_x−P_y)\,dA. \nonumber \]
La même logique implique que la forme de flux du théorème de Green peut également être étendue à une région comportant un nombre infini de trous :
\[\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA. \nonumber \]
Calculez l'intégrale
\[\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy, \nonumber \]
où\(D\) se trouve l'annulus donné par les inégalités polaires\(1≤r≤2\),\(0≤\theta≤2\pi\).
Solution
Bien que\(D\) ce ne soit pas simplement connecté, nous pouvons utiliser la forme étendue du théorème de Green pour calculer l'intégrale. Comme l'intégration se fait sur un anneau, nous convertissons en coordonnées polaires :
\[\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}\]
\(C\)Soit\(\vecs F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩\) n'importe quelle courbe fermée simple dans un plan orienté dans le sens antihoraire. Quelles sont les valeurs possibles de\(\oint_C \vecs F·d\vecs{r}\) ?
Solution
Nous utilisons la forme étendue du théorème de Green pour montrer que c'\(\oint_C \vecs F·d\vecs{r}\)est l'un\(0\) ou l'autre, c'\(−2\pi\)est-à-dire que, quelle que\(C\) soit la complexité de la courbe, l'intégrale de la droite de\(\vecs F\) along ne\(C\) peut avoir qu'une des deux valeurs possibles. Nous considérons deux cas : le cas où\(C\) englobe l'origine et le cas où il\(C\) n'englobe pas l'origine.
Cas 1 : C n'englobe pas l'origine
Dans ce cas, la région délimitée par\(C\) est simplement connectée car le seul trou dans le domaine de\(\vecs F\) se trouve à l'origine. Dans notre discussion, nous avons montré que les partiels croisés\(\vecs F\) satisfont à la condition de partialité croisée. Si nous limitons le domaine de\(\vecs F\) seulement à\(C\) et à la région qu'il englobe, alors\(\vecs F\) ce domaine restreint est désormais défini sur un domaine simplement connecté. Comme il\(\vecs F\) satisfait à la propriété partielle croisée sur son domaine restreint, le champ\(\vecs F\) est conservateur sur cette région simplement connectée et, par conséquent, la circulation\(\oint_C \vecs F·d\vecs{r}\) est nulle.
Cas 2 : C englobe bel et bien l'origine
Dans ce cas, la région délimitée par n'\(C\)est pas simplement connectée car cette région contient un trou à l'origine. \(C_1\)Soit un cercle de rayon a centré à l'origine, de sorte qu'il\(C_1\) se trouve entièrement à l'intérieur de la région délimitée par\(C\) (Figure\(\PageIndex{15}\)). Donnez\(C_1\) une orientation dans le sens horaire.
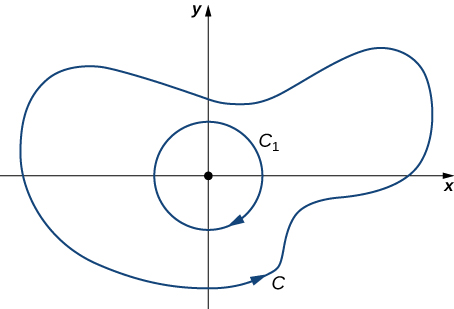
\(D\)Soit la région entre\(C_1\) et\(C\), et\(C\) est orientée dans le sens antihoraire. Selon la version étendue du théorème de Green,
\[\begin{align*} \int_C \vecs F·d\vecs{r}+\int_{C_1}\vecs F·d\vecs{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}\]
et donc
\[\int_C \vecs F·d\vecs{r}=−\int_{C_1} \vecs F·d\vecs{r}. \nonumber \]
Comme\(C_1\) il s'agit d'une courbe spécifique, nous pouvons l'évaluer\(\int_{C_1}\vecs F·d\vecs{r}\). Laissez
\[ x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber \]
être un paramétrage de\(C_1\). Ensuite,
\[\begin{align*} \int_{C_1}\vecs F·d\vecs{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}\]
Par conséquent,\(\int_C F·ds=−2\pi\).
Calculez l'intégrale\(\oint_{\partial D}\vecs F·d\vecs{r}\), où\(D\) est l'anneau donné par les inégalités polaires\(2≤r≤5\)\(0≤\theta≤2\pi\), et\(F(x,y)=⟨x^3,5x+e^y\sin y⟩\).
- Allusion
-
Utilisez la version étendue du théorème de Green.
- Réponse
-
\(105\pi\)
Imaginez que vous êtes un médecin qui vient de recevoir une image par résonance magnétique du cerveau de votre patient. Le cerveau a une tumeur (Figure\(\PageIndex{16}\)). Quelle est la taille de la tumeur ? Pour être précis, quelle est la superficie de la région rouge ? La section transversale rouge de la tumeur a une forme irrégulière et il est donc peu probable que vous puissiez trouver un ensemble d'équations ou d'inégalités pour la région et pouvoir ensuite calculer sa surface par des moyens conventionnels. Vous pouvez obtenir une estimation de la surface en découpant la région en petits carrés (méthode de la somme de Riemann), mais cette méthode donne toujours une réponse avec une certaine erreur.
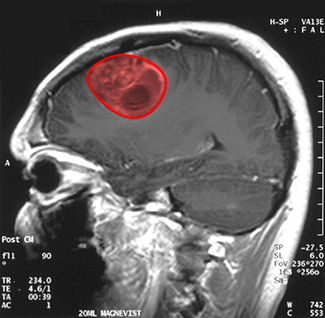
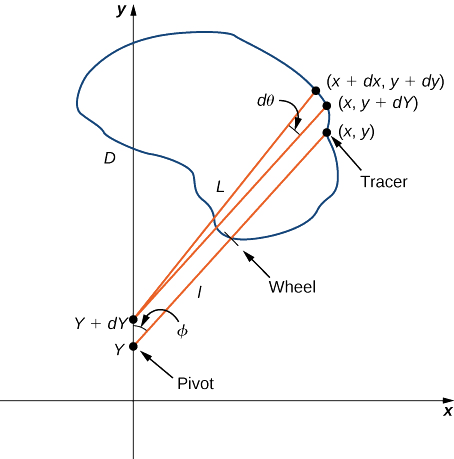
Au lieu d'essayer de mesurer directement la superficie de la région, nous pouvons utiliser un appareil appelé planimètre roulant pour calculer exactement la superficie de la région, simplement en mesurant sa limite. Dans ce projet, vous étudiez le fonctionnement d'un planimètre et vous utilisez le théorème de Green pour montrer que l'appareil calcule correctement la surface.
Un planimètre roulant est un appareil qui mesure la surface d'une région plane en traçant la limite de cette région (Figure\(\PageIndex{17}\)). Pour mesurer la superficie d'une région, il suffit de faire passer le traceur du planimètre autour de la limite de la région. Le planimètre mesure le nombre de tours parcourus par la roue lorsque nous tracons la limite ; l'aire de la forme est proportionnelle à ce nombre de tours de roue. Nous pouvons obtenir l'équation de proportionnalité précise en utilisant le théorème de Green. Lorsque le traceur se déplace autour de la limite de la région, le bras traceur tourne et le rouleau se déplace d'avant en arrière (mais ne tourne pas).
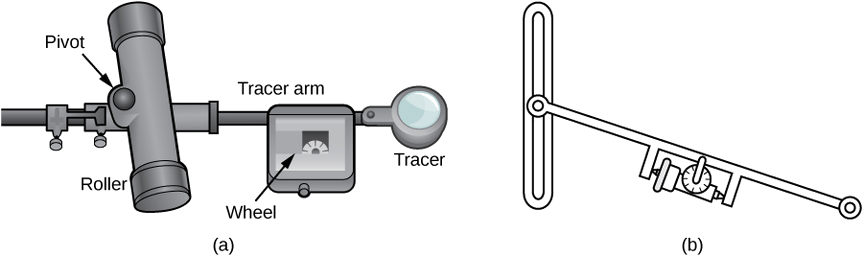
\(C\)Dénotons la limite de la région\(D\), la zone à calculer. Lorsque le traceur traverse une courbe\(C\), supposons que le rouleau se déplace le long de l'axe y (comme le rouleau ne tourne pas, on peut supposer qu'il se déplace le long d'une ligne droite). Utilisez les coordonnées\((x,y)\) pour représenter les points sur la limite\(C\) et les coordonnées\((0,Y)\) pour représenter la position du pivot. Au fur et à mesure du tracé du planimètre\(C\), le pivot se déplace le long de l'axe y tandis que le bras traceur tourne sur le pivot.
Regardez une courte animation d'un planimètre en action.
Commencez l'analyse en prenant en compte le mouvement du traceur lorsqu'il se déplace d'un point\((x,y)\) dans le sens antihoraire jusqu'à un point\((x+dx,y+dy)\) proche de\((x,y)\) (Figure\(\PageIndex{18}\)). Le pivot se déplace également, d'un point\((0,Y)\) à un point proche\((0,Y+dY)\). Dans quelle mesure la roue tourne-t-elle à la suite de ce mouvement ? Pour répondre à cette question, divisez la motion en deux parties. Tout d'abord, faites rouler le pivot le long de l'axe y de\((0,Y)\) à\((0,Y+dY)\) sans faire tourner le bras traceur. Le bras traceur se retrouve alors au point\((x,y+dY)\) tout en maintenant un angle constant\(\phi\) avec l'axe X. Ensuite, faites pivoter le bras traceur d'un angle\(d\theta\) sans déplacer le rouleau. Maintenant, le traceur est au point\((x+dx,y+dy)\). Soit ll la distance entre le pivot et la roue et L la distance entre le pivot et le traceur (la longueur du bras traceur).

- Expliquez pourquoi la distance totale sur laquelle la roue roule selon le petit mouvement que vous venez de décrire est\(\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta\).
- Montrez ça\(\oint_C d\theta=0\).
- Utilisez l'étape 2 pour montrer que la distance de roulement totale de la roue lorsque le traceur traverse la courbe\(C\) est le roulis
total de la roue\(=\dfrac{1}{L}\oint_C xdY\).
Maintenant que vous avez une équation pour la distance de roulement totale de la roue, connectez cette équation au théorème de Green pour calculer la surface\(D\) délimitée par\(C\). - Montrez ça\(x^2+(y−Y)^2=L^2\).
- Supposons que l'orientation du planimètre est celle indiquée sur la figure\(\PageIndex{18}\). Expliquez pourquoi\(Y≤y\) et utilisez cette inégalité pour montrer qu'il existe une valeur unique de\(Y\) pour chaque point\((x,y)\) :\(Y=y=\sqrt{L^2−x^2}\).
- Utilisez l'étape 5 pour montrer que\(dY=dy+\dfrac{x}{L^2−x^2}dx.\)
- Utilisez le théorème de Green pour le montrer\(\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0\).
- Utilisez l'étape 7 pour montrer que le roulis total est
\[\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy. \nonumber \]
Cela a demandé un peu de travail, mais cette équation indique que la variable d'intégration Y de l'étape 3 peut être remplacée par y.
- Utilisez le théorème de Green pour montrer que l'aire de\(D\) est\(\oint_C xdy\). La logique est similaire à celle utilisée pour montrer que la zone de\(\displaystyle D=12\oint_C −y\,dx+x\,dy\).
- Concluez que l'aire de\(D\) est égale à la longueur du bras traceur multipliée par la distance de roulement totale de la roue.
Vous savez maintenant comment fonctionne un planimètre et vous avez utilisé le théorème de Green pour justifier son fonctionnement. Pour calculer l'aire d'une région plane\(D\), utilisez un planimètre pour tracer la limite de la région. La surface de la région est la longueur du bras traceur multipliée par la distance parcourue par la roue.
Concepts clés
- Le théorème de Green relie l'intégrale d'une région connectée à une intégrale au-dessus de la limite de la région. Le théorème de Green est une version du théorème fondamental du calcul dans une dimension supérieure.
- Le théorème de Green se présente sous deux formes : une forme de circulation et une forme de flux. Dans la forme circulatoire, l'integrand est\(\vecs F·\vecs T\). Sous forme de flux, l'integrand est\(\vecs F·\vecs N\).
- Le théorème de Green peut être utilisé pour transformer une intégrale linéaire difficile en une intégrale double plus facile, ou pour transformer une intégrale double difficile en une intégrale linéaire plus facile.
- Un champ vectoriel est exempt de source s'il possède une fonction de flux. Le flux d'un champ vectoriel sans source à travers une courbe fermée est nul, tout comme la circulation d'un champ vectoriel conservateur sur une courbe fermée est nulle.
Équations clés
- Théorème de Green, forme de circulation
\(\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA\), où se\(C\) trouve la limite de\(D\) - Théorème de Green, forme de flux
\(\displaystyle ∮_C\vecs F·\vecs N\,ds=∬_D P_x+Q_y\,dA\), où se\(C\) trouve la limite de\(D\) - Théorème de Green, version étendue
\(\displaystyle ∮_{\partial D}\vecs F·d\vecs{r}=∬_D Q_x−P_y\,dA\)
Lexique
- Théorème de Green
- relie l'intégrale sur une région connectée à une intégrale sur la limite de la région
- fonction de flux
- si\(\vecs F=⟨P,Q⟩\) est un champ vectoriel sans source, alors la fonction stream\(g\) est une fonction telle que\(P=g_y\) et\(Q=−g_x\)


