16.4E : Exercices pour la section 16.4

Last updated
Save as PDF

Page ID: 197906

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices suivants, évaluez les intégrales linéaires en appliquant le théorème de Green.

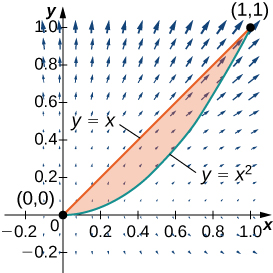
1. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, où$C$ est la trajectoire$(0, 0)$ allant de et le$(1, 1)$ long du graphe$y=x^3$ et de$(1, 1)$ à$(0, 0)$ le long du graphe d'$y=x$orienté dans le sens antihoraire

2. $\displaystyle \int_C 2xy\,dx+(x+y)\,dy$, où$C$ est la limite de la région située entre les graphes de$y=0$ et$y=4−x^2$ orientée dans le sens antihoraire

Réponse: $\displaystyle \int_C2xy\,dx+(x+y)\,dy=\frac{32}{3}$unités de travail

3. $\displaystyle \int_C 2\arctan\left(\frac{y}{x}\right)\,dx+\ln(x^2+y^2)\,dy$, où$C$ est défini par$x=4+2\cos θ,\;y=4\sin θ$ orienté dans le sens antihoraire

4. $\displaystyle \int_C \sin x\cos y\,dx+(xy+\cos x\sin y)\,dy$, où$C$ est la limite de la région située entre les graphes de$y=x$ et$y=\sqrt{x}$ orientée dans le sens antihoraire

Réponse: $\displaystyle \int_C\sin x\cos y\,dx+(xy+\cos x\sin y)\,dy=\frac{1}{12}$unités de travail

5. $\displaystyle \int_C xy\,dx+(x+y)\,dy$, où$C$ est la limite de la région située entre les graphes de$x^2+y^2=1$ et$x^2+y^2=9$ orientée dans le sens antihoraire

6. $\displaystyle ∮_C (−y\,dx+x\,dy)$, où$C$ se compose d'un segment$C_1$ de ligne allant de$(−1,0)$ à$(1, 0)$, suivi de l'arc semi-circulaire$C_2$ allant de l'$(1, 0)$arrière vers$(-1, 0)$

Réponse: $\displaystyle ∮_C (−y\,\,dx+x\,\,dy)=π$unités de travail

Pour les exercices suivants, utilisez le théorème de Green.

7. $C$Soit la courbe composée de segments de ligne allant de$(0, 0)$ à$(1, 1)$ à$(0, 1)$ et retour à$(0, 0)$. Trouvez la valeur de$\displaystyle \int_C xy\,dx+\sqrt{y^2+1}\,dy$.

8. Évaluez l'intégrale de la ligne$\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy$, où$C$ se trouve la limite de la région entre les cercles$x^2+y^2=1$ et$x^2+y^2=4$, et est une courbe orientée positivement.

Réponse: $\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy=0$unités de travail

9. Déterminez la circulation du champ dans le sens antihoraire$\vecs F(x,y)=xy\,\mathbf{\hat i}+y^2\,\mathbf{\hat j}$ autour et au-dessus de la limite de la région délimitée par des courbes$y=x^2$ et$y=x$ dans le premier quadrant et orientée dans le sens antihoraire.

$CNX_Calc_Figure_16_04_201.jpg$

10. Évaluez$\displaystyle ∮_C y^3\,dx−x^3y^2\,dy$, où$C$ se trouve le cercle de rayon orienté positivement$2$ centré sur l'origine.

Réponse: $\displaystyle ∮_C y^3\,dx−x^3y^2\,dy=−20π$unités de travail

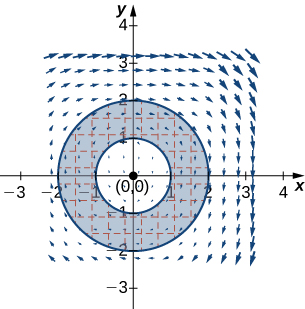
11. Evaluer$\displaystyle ∮_C y^3\,dx−x^3\,dy$, où$C$ inclut les deux cercles de rayon$2$ et de rayon$1$ centrés sur l'origine, tous deux avec une orientation positive.

$CNX_Calc_Figure_16_04_202.jpg$

12. Calculez$\displaystyle ∮_C −x^2y\,dx+xy^2\,dy$, où$C$ est un cercle de rayon$2$ centré à l'origine et orienté dans le sens antihoraire.

Réponse: $\displaystyle ∮_C −x^2y\,dx+xy^2\,dy=8π$unités de travail

13. Calculez l'intégrale$\displaystyle ∮_C 2[y+x\sin(y)]\,dx+[x^2\cos(y)−3y^2]\,dy$ le long$C$ d'un triangle avec des sommets$(0, 0), \,(1, 0)$ et$(1, 1)$, dans le sens antihoraire, en utilisant le théorème de Green.

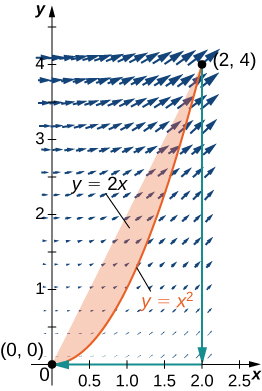
14. Évaluez l'intégrale$\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy$, où$C$ est la courbe qui suit la parabole$y=x^2$ à partir de$(0,0), \,(2,4),$ puis la droite de$(2, 4)$ à$(2, 0)$ et enfin la droite de$(2, 0)$ à$(0, 0)$.

$CNX_Calc_Figure_16_04_203.jpg$

Réponse: $\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy=0$unités de travail

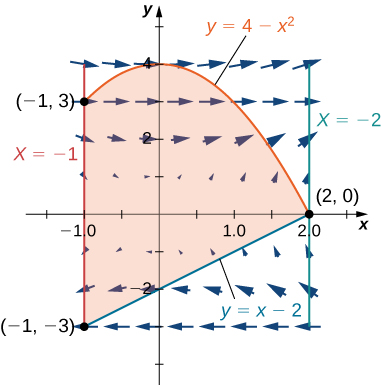
15. Évaluez l'intégrale de la ligne$\displaystyle ∮_C (y−\sin(y)\cos(y))\,dx+2x\sin^2(y)\,dy$, qui$C$ est orientée dans le sens antihoraire autour de la région délimitée par$x=−1, \,x=2, \,y=4−x^2$, et$y=x−2.$

$CNX_Calc_Figure_16_04_204.jpg$

Pour les exercices suivants, utilisez le théorème de Green pour trouver la zone.

16. Détermine l'aire entre l'ellipse$\frac{x^2}{9}+\frac{y^2}{4}=1$ et le cercle$x^2+y^2=25$.

Réponse: $A=19π\;\text{units}^2$

17. Détermine l'aire de la région délimitée par une équation paramétrique

$\vecs p(θ)=(\cos(θ)−\cos^2(θ))\,\mathbf{\hat i}+(\sin(θ)−\cos(θ)\sin(θ))\,\mathbf{\hat j}$pour$0≤θ≤2π.$

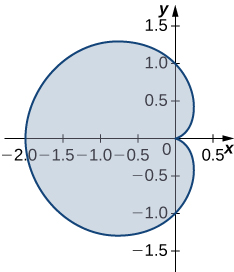
$CNX_Calc_Figure_16_04_205.jpg$

18. Trouvez la zone de la région délimitée par l'hypocycloïde$\vecs r(t)=\cos^3(t)\,\mathbf{\hat i}+\sin^3(t)\,\mathbf{\hat j}$. La courbe est paramétrée par$t∈[0,2π].$

Réponse: $A=\frac{3}{8π}\;\text{units}^2$

19. Détermine l'aire d'un pentagone avec des sommets$(0,4), \,(4,1), \,(3,0), \,(−1,−1),$ et$(−2,2)$.

20. Utilisez le théorème de Green pour évaluer$\displaystyle \int_{C^+}(y^2+x^3)\,dx+x^4\,dy$ où$C^+$ est le périmètre du carré$[0,1]×[0,1]$ orienté dans le sens antihoraire.

Réponse: $\displaystyle \int_{C^+} (y^2+x^3)\,dx+x^4\,dy=0$

21. Utilisez le théorème de Green pour prouver que l'aire d'un disque avec un rayon$a$ est$A=πa^2\;\text{units}^2$.

22. Utilisez le théorème de Green pour déterminer l'aire d'une boucle d'une rose à quatre feuilles$r=3\sin 2θ$. (Astuce :$x\,dy−y\,dx=r^2\,dθ$).

Réponse: $A=\frac{9π}{8}\;\text{units}^2$

23. Utilisez le théorème de Green pour déterminer l'aire sous une arche de la cycloïde donnée par les équations paramétriques :$x=t−\sin t,\;y=1−\cos t,\;t≥0.$

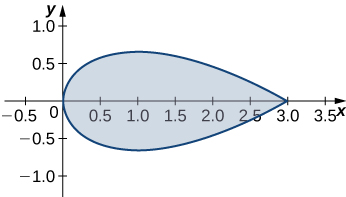
24. Utilisez le théorème de Green pour déterminer l'aire de la région délimitée par la courbe

$\vecs r(t)=t^2\,\mathbf{\hat i}+\left(\frac{t^3}{3}−t\right)\,\mathbf{\hat j},$pour$−\sqrt{3}≤t≤\sqrt{3}$.

$CNX_Calc_Figure_16_04_206.jpg$

Réponse: $A=\frac{8\sqrt{3}}{5}\;\text{units}^2$

25. [T] Évaluez le théorème de Green à l'aide d'un système d'algèbre informatique pour évaluer l'intégrale$\displaystyle \int_C xe^y\,dx+e^x\,dy$, où$C$ est le cercle donné par$x^2+y^2=4$ et est orienté dans le sens antihoraire.

26. Évaluez$\displaystyle \int_C(x^2y−2xy+y^2)\,ds$, où$C$ se trouve la limite du carré unitaire$0≤x≤1,\;0≤y≤1$, parcourue dans le sens antihoraire.

Réponse: $\displaystyle \int_C (x^2y−2xy+y^2)\,ds=3$

27. Évaluez$\displaystyle \int_C \frac{−(y+2)\,dx+(x−1)\,dy}{(x−1)^2+(y+2)^2}$, où$C$ se trouve une courbe fermée simple dont l'intérieur ne contient pas de point$(1,−2)$ parcouru dans le sens antihoraire.

28. Évaluez$\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}$, où se$C$ trouve une courbe fermée simple et lisse, par morceaux, entourant l'origine, parcourue dans le sens antihoraire.

Réponse: $\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}=2π$

Pour les exercices suivants, utilisez le théorème de Green pour calculer le travail effectué par la force$\vecs F$ sur une particule qui se déplace dans le sens antihoraire sur une trajectoire fermée$C$.

29. $\vecs F(x,y)=xy\,\mathbf{\hat i}+(x+y)\,\mathbf{\hat j}, \quad C:x^2+y^2=4$

30. $\vecs F(x,y)=(x^{3/2}−3y)\,\mathbf{\hat i}+(6x+5\sqrt{y})\,\mathbf{\hat j}, \quad C$: boundary of a triangle with vertices $(0, 0), \,(5, 0),$ and $(0, 5)$

Answer: $W=\frac{225}{2}$ units of work

31. Evaluate $\displaystyle \int_C (2x^3−y^3)\,dx+(x^3+y^3)\,dy$, where $C$ is a unit circle oriented in the counterclockwise direction.

32. A particle starts at point $(−2,0)$, moves along the $x$-axis to $(2, 0)$, and then travels along semicircle $y=\sqrt{4−x^2}$ to the starting point. Use Green’s theorem to find the work done on this particle by force field $\vecs F(x,y)=x\,\mathbf{\hat i}+(x^3+3xy^2)\,\mathbf{\hat j}$.

Answer: $W=12π$ units of work

33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius $2$ in a counterclockwise direction. Sandra skates once around a circle of radius $3$, also in the counterclockwise direction. Suppose the force of the wind at point $(x,y)$ is $\vecs F(x,y)=(x^2y+10y)\,\mathbf{\hat i}+(x^3+2xy^2)\,\mathbf{\hat j}$. Use Green’s theorem to determine who does more work.

34. Use Green’s theorem to find the work done by force field $\vecs F(x,y)=(3y−4x)\,\mathbf{\hat i}+(4x−y)\,\mathbf{\hat j}$ when an object moves once counterclockwise around ellipse $4x^2+y^2=4.$

Answer: $W=2π$ units of work

35. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C e^{2x}\sin 2y\,dx+e^{2x}\cos 2y\,dy$, where $C$ is ellipse $9(x−1)^2+4(y−3)^2=36$ oriented counterclockwise.

36. Evaluate line integral $\displaystyle ∮_C y^2\,dx+x^2\,dy$, where $C$ is the boundary of a triangle with vertices $(0,0), \,(1,1)$, and $(1,0)$, with the counterclockwise orientation.

Answer: $\displaystyle ∮_C y^2\,dx+x^2\,dy=\frac{1}{3}$ units of work

37. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \vecs h·d\vecs r$ if $\vecs h(x,y)=e^y\,\mathbf{\hat i}−\sin πx\,\mathbf{\hat j}$, where $C$ is a triangle with vertices $(1, 0), \,(0, 1),$ and $(−1,0),$ traversed counterclockwise.

38. Use Green’s theorem to evaluate line integral $\displaystyle \int_C\sqrt{1+x^3}\,dx+2xy\,dy$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 3)$ oriented clockwise.

Answer: $\displaystyle \int_C \sqrt{1+x^3}\,dx+2xy\,dy=3$ units of work

39. Use Green’s theorem to evaluate line integral $\displaystyle \int_C x^2y\,dx−xy^2\,dy$ where $C$ is a circle $x^2+y^2=4$ oriented counterclockwise.

40. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy$ where $C$ is circle $x^2+y^2=9$ oriented in the counterclockwise direction.

Answer: $\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy=36π$ units of work

41. Use Green’s theorem to evaluate line integral $\displaystyle \int_C (3x−5y)\,dx+(x−6y)\,dy$, where $C$ is ellipse $\frac{x^2}{4}+y^2=1$ and is oriented in the counterclockwise direction.

$A horizontal oval oriented counterclockwise with vertices at (-2,0), (0,-1), (2,0), and (0,1). The region enclosed is shaded.$

42. Let $C$ be a triangular closed curve from $(0, 0)$ to $(1, 0)$ to $(1, 1)$ and finally back to $(0, 0).$ Let $\vecs F(x,y)=4y\,\mathbf{\hat i}+6x^2\,\mathbf{\hat j}.$ Use Green’s theorem to evaluate $\displaystyle ∮_C\vecs F·d\vecs r.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=2$ units of work

43. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C y\,dx−x\,dy$, where $C$ is circle $x^2+y^2=a^2$ oriented in the clockwise direction.

44. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy,$ where $C$ is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy=0$ units of work

45. Use Green’s theorem to evaluate line integral $\displaystyle ∮_C \left(y−\ln(x^2+y^2)\right)\,dx+\left(2\arctan \frac{y}{x}\right)\,dy,$ where $C$ is the positively oriented circle $(x−2)^2+(y−3)^2=1.$

46. Use Green’s theorem to evaluate $\displaystyle ∮_C xy\,dx+x^3y^3\,dy,$ where $C$ is a triangle with vertices $(0, 0), \,(1, 0),$ and $(1, 2)$ with positive orientation.

Answer: $\displaystyle ∮_C xy\,dx+x^3y^3\,dy=2221$ units of work

47. Use Green’s theorem to evaluate line integral $\displaystyle \int_C \sin y\,dx+x\cos y\,dy,$ where $C$ is ellipse $x^2+xy+y^2=1$ oriented in the counterclockwise direction.

48. Let $\vecs F(x,y)=\left(\cos(x^5)−13y^3\right)\,\mathbf{\hat i}+13x^3\,\mathbf{\hat j}.$ Find the counterclockwise circulation $\displaystyle ∮_C\vecs F·d\vecs r,$ where $C$ is a curve consisting of the line segment joining $(−2,0)$ and $(−1,0),$ half circle $y=\sqrt{1−x^2},$ the line segment joining $(1, 0)$ and $(2, 0),$ and half circle $y=\sqrt{4−x^2}.$

Answer: $\displaystyle ∮_C\vecs F·d\vecs r=15π^4$ units of work

49. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \sin(x^3)\,dx+2ye^{x^2}\,dy,$ where $C$ is a triangular closed curve that connects the points $(0, 0), \,(2, 2),$ and $(0, 2)$ counterclockwise.

50. Let $C$ be the boundary of square $0≤x≤π,\;0≤y≤π,$ traversed counterclockwise. Use Green’s theorem to find $\displaystyle ∫_C \sin(x+y)\,dx+\cos(x+y)\,dy.$

Answer: $\displaystyle \int_C\sin(x+y)\,dx+\cos(x+y)\,dy=4$ units of work

51. Use Green’s theorem to evaluate line integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and $C$ is a triangle bounded by $y=0,\;x=3,$ and $y=x,$ oriented counterclockwise.

52. Use Green’s Theorem to evaluate integral $\displaystyle ∫_C \vecs F·d\vecs r,$ where $\vecs F(x,y)=(xy^2)\,\mathbf{\hat i}+x\,\mathbf{\hat j},$ and $C$ is a unit circle oriented in the counterclockwise direction.

Answer: $\displaystyle ∫_C \vecs F·d\vecs r=π$ units of work

53. Use Green’s theorem in a plane to evaluate line integral $\displaystyle ∮_C (xy+y^2)\,dx+x^2\,dy,$ where $C$ is a closed curve of a region bounded by $y=x$ and $y=x^2$ oriented in the counterclockwise direction.

54. Calculate the outward flux of $\vecs F(x,y)=−x\,\mathbf{\hat i}+2y\,\mathbf{\hat j}$ over a square with corners $(±1,\,±1),$ where the unit normal is outward pointing and oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C\vecs F·\vecs N \,ds=4$

55. [T] Let $C$ be circle $x^2+y^2=4$ oriented in the counterclockwise direction. Evaluate $\displaystyle ∮_C \left[\left(3y−e^{\arctan x})\,dx+(7x+\sqrt{y^4+1}\right)\,dy\right]$ using a computer algebra system.

56. Find the flux of field $\vecs F(x,y)=−x\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ across $x^2+y^2=16$ oriented in the counterclockwise direction.

Answer: $\displaystyle ∮_C \vecs F·\vecs N\,ds=32π$

57. Let $\vecs F=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},$ and let $C$ be a triangle bounded by $y=0, \,x=3,$ and $y=x$ oriented in the counterclockwise direction. Find the outward flux of $\vecs F$ through $C$.

58. [T] Let $C$ be unit circle $x^2+y^2=1$ traversed once counterclockwise. Evaluate $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy$ by using a computer algebra system.

Answer: $\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy=4.7124$ units of work

59. [T] Find the outward flux of vector field $\vecs F(x,y)=xy^2\,\mathbf{\hat i}+x^2y\,\mathbf{\hat j}$ across the boundary of annulus $R=\big\{(x,y):1≤x^2+y^2≤4\big\}=\big\{(r,θ):1≤r≤2,\,0≤θ≤2π\big\}$ using a computer algebra system.

60. Consider region $R$ bounded by parabolas $y=x^2$ and $x=y^2.$ Let $C$ be the boundary of $R$ oriented counterclockwise. Use Green’s theorem to evaluate $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy.$

Answer: $\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy=13$ units of work

Contributors

Template:contribopenstaxcalc