16.5 : Divergence et courbure
- Page ID
- 197872
- Déterminez la divergence par rapport à la formule pour un champ vectoriel donné.
- Déterminez la courbure à partir de la formule pour un champ vectoriel donné.
- Utilisez les propriétés de courbure et de divergence pour déterminer si un champ vectoriel est conservateur.
Dans cette section, nous examinons deux opérations importantes sur un champ vectoriel : la divergence et la courbure. Ils sont importants dans le domaine du calcul pour plusieurs raisons, notamment l'utilisation de la courbure et de la divergence pour développer certaines versions plus dimensionnelles du théorème fondamental du calcul. De plus, la courbure et la divergence apparaissent dans les descriptions mathématiques de la mécanique des fluides, de l'électromagnétisme et de la théorie de l'élasticité, qui sont des concepts importants en physique et en ingénierie. Nous pouvons également appliquer la courbure et la divergence à d'autres concepts que nous avons déjà explorés. Par exemple, dans certaines conditions, un champ vectoriel est conservateur si et seulement si sa courbure est nulle.
En plus de définir la courbure et la divergence, nous examinons certaines interprétations physiques de celles-ci et montrons leur relation avec des champs vectoriels conservateurs et sans source.
Différence
La divergence est une opération sur un champ vectoriel qui nous indique comment le champ se comporte en direction ou en s'éloignant d'un point. Localement, la divergence d'un champ\(\vecs{F}\) vectoriel\(\mathbb{R}^3\) à l'intérieur\(\mathbb{R}^2\) ou à un point particulier\(P\) est une mesure de la « capacité de sortie » du champ vectoriel à\(P\). Si\(\vecs{F}\) représente la vitesse d'un fluide, alors la divergence de\(\vecs{F}\) at\(P\) mesure le taux net de variation par rapport au temps de la quantité de fluide qui s'écoule\(P\) (tendance du fluide à s'écouler « hors » de P). En particulier, si la quantité de fluide entrant\(P\) est identique à la quantité sortant, alors la divergence à\(P\) est nulle.
S'il s'\(\vecs{F} = \langle P,Q,R \rangle\)agit d'un champ vectoriel dans\(\mathbb{R}^3\)\(P_x, \, Q_y, \) et que\(R_z\) tout existe, alors la divergence de\(\vecs{F}\) est définie par
\[\begin{align} \text{div}\, F &= P_x + Q_y + R_z \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}. \end{align} \nonumber \]
Notez que la divergence d'un champ vectoriel n'est pas un champ vectoriel, mais une fonction scalaire. En termes d'opérateur de gradient
\[\vecs \nabla = \langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \rangle \nonumber \]
la divergence peut être écrite symboliquement sous la forme d'un produit scalaire
\[\text{div}\, \vecs F = \vecs \nabla \cdot \vecs{F}. \nonumber \]
Notez qu'il s'agit simplement d'une notation utile, car le produit scalaire d'un vecteur d'opérateurs et d'un vecteur de fonctions n'est pas défini de manière significative compte tenu de notre définition actuelle du produit scalaire.
S'il s'\(\vecs{F} = \langle P,Q \rangle\)agit d'un champ vectoriel dans\(\mathbb{R}^2\)\(P_x\) et\(Q_y\) que les deux existent, alors la divergence de\(\vecs{F}\) est définie de la même manière que
\[\begin{align*} \text{div}\, \vecs{F} &= P_x + Q_y \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \\[4pt] &= \vecs \nabla \cdot \vecs{F}. \end{align*}\]
Pour illustrer ce point, considérez les deux champs vectoriels de la figure\(\PageIndex{1}\). À tout moment, la quantité entrante est la même que la quantité sortant, de sorte qu'à chaque point, la « capacité de sortie » du champ est nulle. Par conséquent, nous nous attendons à ce que la divergence des deux champs soit nulle, et c'est bien le cas, car
\[\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0 \nonumber \]
et
\[\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0. \nonumber \]
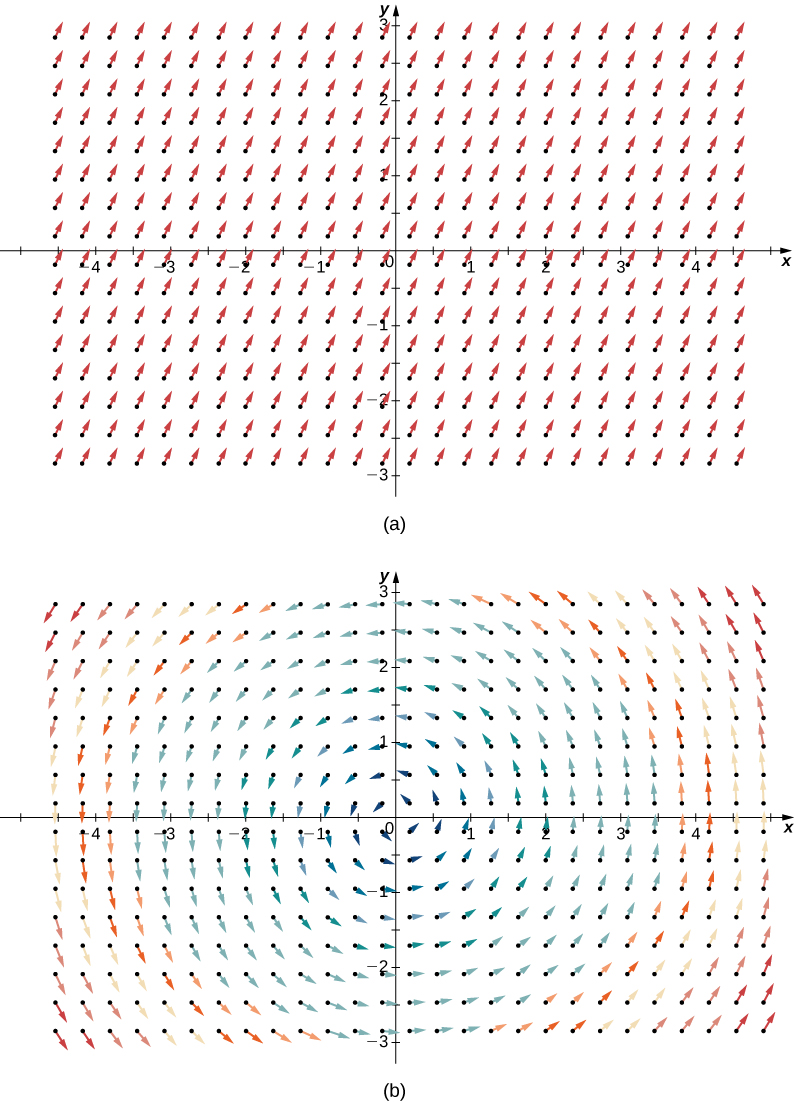
En revanche, considérez le champ vectoriel radial\(\vecs{R} (x,y) = \langle -x, -y \rangle\) dans la figure\(\PageIndex{2}\). À tout moment donné, plus de fluide entre qu'il n'en sort, et par conséquent, la « sortie » du champ est négative. Nous nous attendons à ce que la divergence de ce champ soit négative, et c'est bien le cas, car
\[\text{div}(\vecs{R}) = \dfrac{\partial}{\partial x} (-x) + \dfrac{\partial}{\partial y} (-y) = -2. \nonumber \]
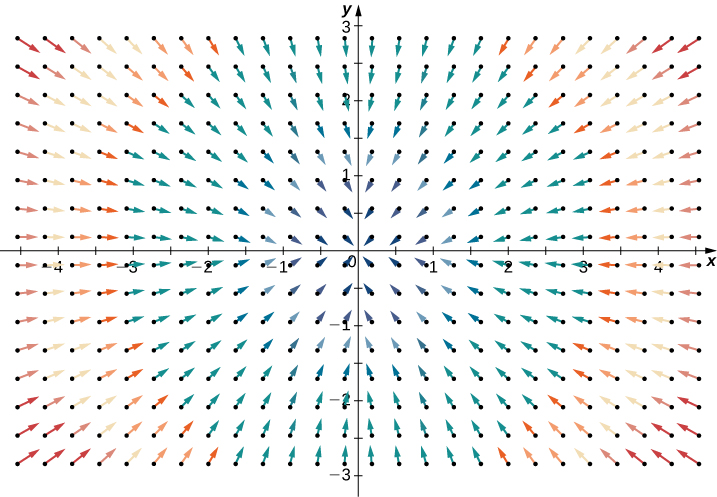
Pour avoir une idée globale de ce que la divergence nous indique, supposons qu'un champ vectoriel\(\mathbb{R}^2\) représente la vitesse d'un fluide. Imaginez prendre un cercle élastique (un cercle dont la forme peut être modifiée par le champ vectoriel) et le déposer dans un fluide. Si le cercle conserve sa surface exacte lorsqu'il traverse le fluide, la divergence est nulle. Cela se produirait pour les deux champs vectoriels de la figure\(\PageIndex{1}\). En revanche, si la forme du cercle est déformée de telle sorte que sa surface se rétrécit ou s'élargit, la divergence n'est pas nulle. Imaginez que vous déposez un tel cercle élastique dans le champ vectoriel radial de la Figure\(\PageIndex{2}\) afin que le centre du cercle atterrisse au point\((3, 3)\). Le cercle se dirigeait vers l'origine et, ce faisant, l'avant du cercle se déplaçait plus lentement que l'arrière, ce qui provoquait un « froissement » du cercle et une perte de surface. C'est ainsi que vous pouvez voir une divergence négative.
Si\(\vecs{F}(x,y,z) = e^x \hat{i} + yz \hat{j} - yz^2 \hat{k}\), alors trouvez la divergence de\(\vecs{F}\) at\((0,2,-1)\).
Solution
La divergence de\(\vecs{F}\) est
\[\dfrac{\partial}{\partial x} (e^x) + \dfrac{\partial}{\partial y}(yz) - \dfrac{\partial}{\partial z} (y z^2) = e^x + z - 2yz. \nonumber \]
Par conséquent, la divergence à\((0,2,-1)\) est\(e^0 - 1 + 4 = 4\). Si\(\vecs{F}\) représente la vitesse d'un fluide, alors plus de liquide s'écoule qu'il n'entre en un point\((0,2,-1)\).
Trouvez\(\text{div}\, \vecs{F}\) pour
\[\vecs{F}(x,y,z) = \langle xy, \, 5-z^2, \, x^2 + y^2 \rangle \nonumber. \nonumber \]
- Allusion
-
Suivez l'exemple\(\PageIndex{1}\).
- Réponse
-
\(\text{div}\, \vecs{F} = y \)
Une autre application de la divergence consiste à détecter si un champ est exempt de source. Rappelez-vous qu'un champ sans source est un champ vectoriel doté d'une fonction de flux ; de manière équivalente, un champ sans source est un champ dont le flux est nul le long d'une courbe fermée. Les deux théorèmes suivants indiquent que, dans certaines conditions, les champs vectoriels sans source sont précisément les champs vectoriels à divergence nulle.
S'il s'\(\vecs{F} = \langle P,Q \rangle\)agit d'un champ vectoriel continu sans source avec des fonctions de composants différenciables, alors\(\text{div}\, \vecs{F} = 0\).
Comme il\(\vecs{F}\) est sans source, il existe une fonction\(g(x,y)\) avec\(g_y = P\) et\(-g_x = Q\). Donc,\(\vecs{F} = \langle g_y, -g_x \rangle\) et\(\text{div}\, \vecs{F} = g_{yx} - g_{xy} = 0\) selon le théorème de Clairaut.
\(\square\)
L'inverse de la divergence d'un champ vectoriel sans source est vrai sur des régions simplement connectées, mais la preuve est trop technique pour être incluse ici. Ainsi, nous avons le théorème suivant, qui permet de tester si un champ vectoriel\(\mathbb{R}^2\) est exempt de source.
\(\vecs{F} = \langle P,Q \rangle \)Soit un champ vectoriel continu avec des fonctions de composants différenciables avec un domaine simplement connecté. Alors,\(\text{div}\, \vecs{F} = 0\) si et seulement si\(\vecs{F}\) c'est sans source.
Est-ce que Field\(\vecs{F} (x,y) = \langle x^2 y, \, 5 - xy^2 \rangle\) Source est gratuit ?
Solution
Notez que le domaine\(\mathbb{R}^2\) de\(\vecs{F}\) est simplement connecté. En outre,\(\vecs{F}\) est continu avec des fonctions de composants différenciables. Par conséquent, nous pouvons utiliser le test de divergence pour les champs vectoriels sans source pour analyser\(\vecs{F}\). La divergence de\(\vecs{F}\) est
\[\dfrac{\partial}{\partial x} (x^2 y) + \dfrac{\partial}{\partial y} (5 - xy^2 ) = 2xy - 2xy = 0. \nonumber \]
Par conséquent,\(\vecs{F}\) est exempt de source selon le test de divergence pour les champs vectoriels sans source.
\(\vecs{F} (x,y) = \langle -ay, bx \rangle\)Soit un champ de rotation où\(a\) et\(b\) sont des constantes positives. La\(\vecs{F}\) source est-elle gratuite ?
- Allusion
-
Calculez la divergence.
- Réponse
-
Oui
Rappelons que la forme de flux du théorème de Green indique que
\[\oint_C \vecs F \cdot \vecs N \; ds = \iint_D P_x + Q_y \;dA, \nonumber \]
où\(C\) est une simple courbe fermée et\(D\) est la région délimitée par\(C\). Depuis\(P_x + Q_y = \text{div}\,\vecs F\), le théorème de Green est parfois écrit comme
\[\oint_C \vecs F \cdot \vecs N\; ds = \iint_D \text{div}\, \vecs F \;dA. \nonumber \]
Par conséquent, le théorème de Green peut être écrit en termes de divergence. Si nous considérons la divergence comme une sorte de dérivée, alors le théorème de Green dit que la « dérivée » d'\(\vecs{F}\)une région peut être traduite en une droite intégrale\(\vecs{F}\) le long de la limite de la région. Ceci est analogue au théorème fondamental du calcul, dans lequel la dérivée d'une fonction\(f\) sur un segment de ligne\([a,b]\) peut être traduite en une déclaration\(f\) sur la limite de\([a,b]\). En utilisant la divergence, nous pouvons voir que le théorème de Green est un analogue dimensionnel supérieur du théorème fondamental du calcul.
Nous pouvons utiliser tout ce que nous avons appris en matière d'application de la divergence. \(\vecs{v}\)Soit un champ vectoriel modélisant la vitesse d'un fluide. Puisque la divergence d'\(\vecs{v}\)au point\(P\) mesure le « débit sortant » du fluide à\(P\),\(\text{div}\, v(P) > 0\) cela implique qu'il y a plus de liquide qui sort\(P\) que de liquide entre. De même,\(\text{div}\, v(P) < 0\) cela implique\(P\) que plus il y a de liquide entrant qu'il n'en sort, et\(\text{div}\, \vecs{v}(P) = 0\) implique que la même quantité de fluide entre et sort.
Supposons qu'il\(\vecs{v}(x,y) = \langle -xy,y \rangle, \, y > 0\) modélise l'écoulement d'un fluide. Y a-t-il plus de liquide qui entre dans le point\((1,4)\) qu'il n'en sort ?
Solution
Pour déterminer si plus de liquide entre\((1,4)\) qu'il n'en sort, nous calculons la divergence de\(\vecs v\) at\((1,4)\) :
\[div(\vecs{v}) = \dfrac{\partial}{\partial x} (-xy) + \dfrac{\partial}{\partial y} (y) = -y + 1. \nonumber \]
Pour trouver la divergence,\((1,4)\) remplacez le point par la divergence :\(-4 + 1 = -3\). Comme la divergence de\(\vecs v\) at\((1,4)\) est négative, plus de liquide entre qu'il n'en sort (Figure\(\PageIndex{4}\)).

Pour le champ vectoriel\(\vecs{v}(x,y) = \langle -xy, y \rangle , \, y > 0\), trouvez tous les points de\(P\) telle sorte que la quantité de fluide entrant\(P\) soit égale à la quantité de fluide sortant\(P\).
- Allusion
-
Déterminez où la divergence est nulle.
- Réponse
-
Tous les points sont en ligne\(y = 1\).
Boucle
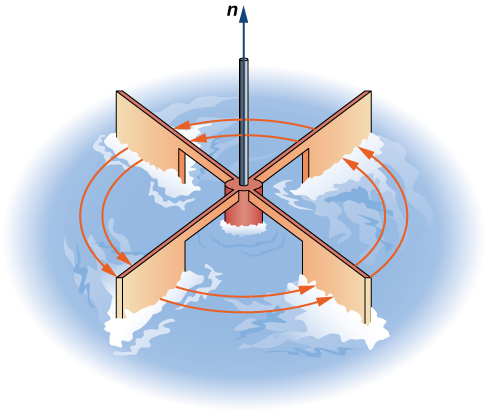
La deuxième opération sur un champ vectoriel que nous examinons est la boucle, qui mesure l'étendue de la rotation du champ autour d'un point. Supposons que cela\(\vecs{F}\) représente le champ de vitesse d'un fluide. Ensuite, la courbure d'\(\vecs{F}\)un point\(P\) est un vecteur qui mesure la tendance des particules proches de\(P\) tourner autour de l'axe qui pointe dans la direction de ce vecteur. L'amplitude du vecteur de courbure à\(P\) mesure la rapidité avec laquelle les particules tournent autour de cet axe. En d'autres termes, la courbure en un point est une mesure du « spin » du champ vectoriel à ce point. Visuellement, imaginez placer une roue à aubes dans un fluide à\(P\), avec l'axe de la roue à aubes aligné sur le vecteur de courbure (Figure\(\PageIndex{5}\)). La courbure mesure la tendance de la roue à aubes à tourner.
Examinez les champs vectoriels de la figure\(\PageIndex{1}\). Dans la partie (a), le champ vectoriel est constant et il n'y a aucun spin en aucun point. Par conséquent, nous nous attendons à ce que la courbure du champ soit nulle, et c'est bien le cas. La partie (b) montre un champ de rotation, de sorte que le champ a une rotation. En particulier, si vous placez une roue à aubes dans un champ en tout point de telle sorte que son axe soit perpendiculaire à un plan, la roue pivote dans le sens antihoraire. Par conséquent, nous nous attendons à ce que la courbure du champ soit différente de zéro, et c'est bien le cas (la boucle l'est\(2\,\mathbf{\hat k}\)).
Pour voir ce que la courbure mesure globalement, imaginez laisser tomber une feuille dans le liquide. Lorsque la feuille se déplace avec le flux de fluide, la courbure mesure la tendance de la feuille à tourner. Si la courbure est nulle, la feuille ne tourne pas lorsqu'elle se déplace dans le fluide.
S'il s'\(\vecs{F} = \langle P,Q,R \rangle\)agit d'un champ vectoriel dans et\(\mathbb{R}^3\)\(P_x, \, Q_y\), et que\(R_z\) tout existe, alors la boucle de\(\vecs{F}\) est définie par
\ [\ begin {align} \ text {curl} \, \ vecs {F} &= (R_y - Q_z) \, \ mathbf {\ hat i} + (P_z - R_x) \, \ mathbf {\ hat j} + (Q_x - P_y) \, \ mathbf {\ hat k} \ \ [4pt]
&= \ left (\ dfrac {\ partial R} {\ partial y} - \ dfrac {\ partial Q} {\ partial z} \ right) \, \ mathbf {\ hat i} + \ left (\ dfrac {\ partial P} {\ partial z} - \ dfrac {\ partial R} {\ partial x} \ right) \, \ mathbf {\ hat j} + \ left (\ dfrac {\ partial Q} {\ partial x} - \ dfrac {\ partial P} {\ partial y} \ right) \, \ mathbf {\ hat k}. \ end {align} \ nonnumber \]
Notez que la courbure d'un champ vectoriel est un champ vectoriel, contrairement à la divergence.
La définition de la boucle peut être difficile à retenir. Pour vous aider à nous en souvenir, nous utilisons la notation\(\vecs \nabla \times \vecs{F}\) pour désigner un « déterminant » qui donne la formule de la boucle :
\[\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \]
Le déterminant de cette matrice est
\[(R_y - Q_z) \,\mathbf{\hat i} - (R_x - P_z) \,\mathbf{\hat j} + (Q_x - P_y) \,\mathbf{\hat k} = (R_y - Q_z) \,\mathbf{\hat i} + (P_z - R_x) \,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} = \text{curl}\, \vecs{F}. \nonumber \]
Ainsi, cette matrice est un moyen d'aider à se souvenir de la formule de la boucle. Gardez toutefois à l'esprit que le mot déterminant est utilisé de manière très vague. Un déterminant n'est pas vraiment défini sur une matrice dont les entrées sont trois vecteurs, trois opérateurs et trois fonctions.
S'il s'\(\vecs{F} = \langle P,Q \rangle\)agit d'un champ vectoriel dans\(\mathbb{R}^2\), alors la boucle de\(\vecs{F}\), par définition, est
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right)\,\mathbf{\hat k}. \nonumber \]
Trouvez la boucle de\(\vecs{F}(P,Q,R) = \langle x^2 z, e^y + xz, xyz \rangle\).
Solution
La boucle est
\[\begin{align*} \text{curl}\, f &= \vecs\nabla \times \vecs{F} \\ &= \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \partial/\partial x & \partial/\partial y & \partial / \partial z \\ P & Q & R \end{vmatrix} \\ &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\ &= (xz - x)\,\mathbf{\hat i} + (x^2 - yz)\,\mathbf{\hat j} + z \,\mathbf{\hat k}. \end{align*}\]
Trouvez la boucle d'\(\vecs{F} = \langle \sin x \, \cos z, \, \sin y \, \sin z, \, \cos x \, \cos y \rangle \)un point\(\left(0, \dfrac{\pi}{2}, \dfrac{\pi}{2} \right)\).
- Allusion
-
Détermine le déterminant de la matrice\(\vecs \nabla \times \vecs{F}\).
- Réponse
-
\(-\hat{i}\)
Trouvez la boucle de\(\vecs{F} = \langle P,Q \rangle = \langle y,0\rangle\).
Solution
Notez que ce champ vectoriel est composé de vecteurs qui sont tous parallèles. En fait, chaque vecteur du champ est parallèle à l'axe X. Ce fait pourrait nous amener à la conclusion que le champ n'a pas de spin et que la courbure est nulle. Pour tester cette théorie, notez que
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = -\,\mathbf{\hat k} \neq \vecs 0. \nonumber \]
Par conséquent, ce champ vectoriel possède un spin. Pour comprendre pourquoi, imaginez placer une roue à aubes à n'importe quel point du premier quadrant (Figure\(\PageIndex{6}\)). Les magnitudes plus grandes des vecteurs situés en haut de la roue entraînent la rotation de la roue. La roue tourne dans le sens des aiguilles d'une montre (négatif), ce qui fait que le coefficient de la boucle est négatif.
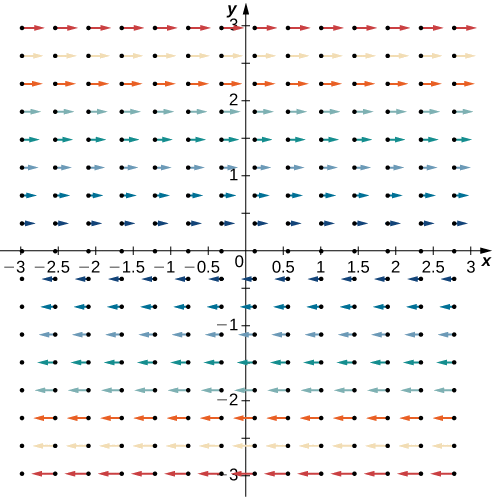
Notez que s'il s'\(\vecs{F} = \langle P,Q\rangle\)agit d'un champ vectoriel dans un plan, alors\(\text{curl}\, \vecs{F} \cdot \mathbf{\hat k} = (Q_x - P_y)\,\mathbf{\hat k} \cdot \mathbf{\hat k} = Q_x - P_y\). Par conséquent, la forme de circulation du théorème de Green est parfois écrite comme
\[\oint_C \vecs{F} \cdot d\vecs{r} = \iint_D \text{curl}\, \vecs F \cdot \,\mathbf{\hat k}\,dA, \nonumber \]
où\(C\) est une simple courbe fermée et\(D\) est la région délimitée par\(C\). Par conséquent, la forme circulatoire du théorème de Green peut être écrite en termes de boucle. Si nous considérons la courbure comme une sorte de dérivée, alors le théorème de Green dit que la « dérivée » d'\(\vecs{F}\)une région peut être traduite en une droite intégrale\(\vecs{F}\) le long de la limite de la région. Ceci est analogue au théorème fondamental du calcul, dans lequel la dérivée d'une fonction\(f\) sur un segment de ligne\([a,b]\) peut être traduite en une déclaration\(f\) sur la limite de\([a,b]\). En utilisant curl, nous pouvons voir que la forme de circulation du théorème de Green est un analogue dimensionnel supérieur du théorème fondamental du calcul.
Nous pouvons maintenant utiliser ce que nous avons appris sur la courbure pour montrer que les champs gravitationnels n'ont aucune « rotation ». Supposons qu'il y ait un objet à l'origine avec une masse\(m_1\) à l'origine et un objet avec une masse\(m_2\). Rappelons que la force gravitationnelle que l'objet 1 exerce sur l'objet 2 est donnée par champ.
\[ \vecs{F}(x,y,z) = - Gm_1m_2 \left\langle \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\right\rangle. \nonumber \]
Montrez qu'un champ gravitationnel n'a pas de spin.
Solution
Pour montrer qu'il n'\(\vecs{F}\)a pas de spin, nous calculons sa courbure. Laissez
- \(P(x,y,z) = \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}\),
- \(Q(x,y,z) = \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}\), et
- \(R(x,y,z) = \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\).
Ensuite,
\ [\ begin {align*} \ text {curl} \, \ vecs {F} &= - GM_1m_2 [(R_y - Q_z) \ mathbf {\ hat i} + (P_z - R_x) \ mathbf {\ hat j} + (Q_x - P_y) \ mathbf {\ hat k}] \ \ [4pt]
&= - GM_1m_2 \ begin {pmatrix} \ left (\ dfrac {-3yz} {(x^2 + y^2 + z^2) ^ {5/2}} - \ left (\ dfrac {-3yz} {(x^2 + y^2 + y^2 + z^2) ^ {5/2}} \ right) \ mathbf {\ hat i} \ nonumber \ \ [4pt]
+ \ left (\ dfrac {-3xz} {(x^2 + y^2 + z^2) ^ {5/2}} - \ left (\ dfrac {-3xz} {(x^2 + y^2 + y^2 + z^2) ^ {5/2}} \ right) \ mathbf {\ hat j} \ nonumber \ \ [4pt]
+ \ left (\ dfrac {-3xy} {(x^2 + y^2 + z^2) ^ {5/2}} - \ left (\ dfrac {-3xy} {(x^2 + y^2 + y^2 + z^2) ^ {5/2}} \ droite) \ droite) \ mathbf {\ hat k} \ end {pmatrix} \ \ [4 points]
&= \ vecs 0. \ end {align*} \]
Comme la courbure du champ gravitationnel est nulle, le champ n'a pas de spin.
Field\(\vecs{v}(x,y) = \langle - \dfrac{y}{x^2+y^2}, \dfrac{x}{x^2+y^2} \rangle \) modélise l'écoulement d'un fluide. Montrez que si vous déposez une feuille dans ce fluide, la feuille ne pivote pas au fil du temps.
- Allusion
-
Calculez la boucle.
- Réponse
-
\(\text{curl}\, \vecs{v} = \vecs 0\)
Utiliser Divergence et Curl
Maintenant que nous avons compris les concepts de base de divergence et de courbure, nous pouvons discuter de leurs propriétés et établir des relations entre elles et des champs vectoriels conservateurs.
S'il s'\(\vecs{F}\)agit d'un champ vectoriel\(\mathbb{R}^3\), alors la boucle de\(\vecs{F}\) est également un champ vectoriel dans\(\mathbb{R}^3\). Par conséquent, nous pouvons prendre la divergence d'une boucle. Le théorème suivant indique que le résultat est toujours nul. Ce résultat est utile car il nous permet de montrer que certains champs vectoriels ne sont pas la courbe d'un autre champ. Pour donner à ce résultat une interprétation physique, rappelons que la divergence d'un champ de vitesse\(\vecs{v}\) à un point\(P\) mesure la tendance du fluide correspondant à s'écouler\(P\). Puisque\(\text{div}(\text{curl}\,\vecs v) = 0\), le débit net dans le champ vectoriel en\(\text{curl}\;\vecs v\) tout point est nul. Le fait de prendre la courbe du champ vectoriel\(\vecs{F}\) élimine toute divergence présente dans\(\vecs{F}\).
\(\vecs{F} = \langle P,Q,R \rangle \)Soit un champ vectoriel de\(\mathbb{R}^3\) telle sorte que les fonctions des composants aient toutes des dérivées partielles continues du second ordre. Ensuite,
\[\text{div}(\text{curl}\, \vecs{F}) = \vecs\nabla \cdot (\vecs \nabla \times \vecs F) = 0. \nonumber \]
Selon les définitions de la divergence et de la courbure, et selon le théorème de Clairaut,
\[\begin{align*} \text{div}(\text{curl}\, \vecs{F}) = \text{div}[(R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k}] \\ = R_{yx} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy}\\ = 0. \end{align*}\]
\(\Box\)
Afficher que ce n'\(\vecs{F}(x,y,z) = e^x\,\mathbf{\hat i}+ yz\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\)est pas la courbure d'un autre champ vectoriel. C'est-à-dire, montrez qu'il n'y a pas d'autre vecteur\(\vecs{G}\) avec\(\text{curl} \, \vecs G = \vecs F\).
Solution
Notez que le domaine de\(\vecs{F}\) est entièrement\(\mathbb{R}^3\) et que les partiels de second ordre de\(\vecs{F}\) sont tous continus. Par conséquent, nous pouvons appliquer le théorème précédent à\(\vecs{F}\).
La divergence de\(\vecs{F}\) est\(e^x + z + 2xz\). Si\(\vecs{F}\) c'était la boucle du champ vectoriel\(\vecs{G}\), alors\(\text{div}\, \vecs F = \text{div}(\text{curl} \,\vecs G) = 0\). Mais la divergence de n'\(\vecs{F}\)est pas nulle et n'\(\vecs{F}\)est donc pas la courbure d'un autre champ vectoriel.
Est-il possible\(\vecs G(x,y,z) = \langle \sin x, \, \cos y, \, \sin (xyz)\rangle \) d'être la boucle d'un champ vectoriel ?
- Allusion
-
Trouvez la divergence de\(\vecs{G}\).
- Réponse
-
Non.
Avec les deux théorèmes suivants, nous montrons que s'il s'\(\vecs{F}\)agit d'un champ vectoriel conservateur, sa courbure est nulle, et si le domaine de\(\vecs{F}\) est simplement connecté, alors l'inverse est également vrai. Cela nous donne un autre moyen de vérifier si un champ vectoriel est conservateur.
C'\(\vecs{F} = \langle P,Q,R\rangle\)est conservateur, alors\(\text{curl} \, \vecs{F} = \vecs 0\).
Puisque les champs vectoriels conservateurs satisfont à la propriété des partiels croisés, tous les champs interpartiels de\(\vecs F\) sont égaux. Par conséquent,
\[\begin{align*} \text{curl}\, \vecs{F} &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\[4pt] &= \vecs 0. \end{align*}\]
\(\Box\)
Le même théorème est vrai pour les champs vectoriels dans un plan.
Comme un champ vectoriel conservateur est le gradient d'une fonction scalaire, le théorème précédent indique cela\(\text{curl}\, (\vecs \nabla f) = \vecs 0\) pour n'importe quelle fonction scalaire\(f\). En termes de notation de nos boucles,\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\). Cette équation est logique car le produit croisé d'un vecteur avec lui-même est toujours le vecteur zéro. Parfois, l'équation\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\) est simplifiée en tant que\(\vecs \nabla \times \vecs \nabla = \vecs 0\).
\(\vecs{F} = \langle P,Q,R\rangle\)Soit un champ vectoriel dans l'espace sur un domaine simplement connecté. Si\(\text{curl}\;\vecs F = \vecs 0\), alors\(\vecs{F}\) c'est conservateur.
Depuis\(\text{curl}\, \vecs F = \vecs 0\), nous avons ça\(R_y = Q_z, \, P_z = R_x\), et\(Q_x = P_y\). Par conséquent,\(\vecs{F}\) satisfait à la propriété interpartielle sur un domaine simplement connecté, et la propriété transversale des champs conservateurs implique que\(\vecs{F}\) c'est conservateur.
\(\Box\)
Le même théorème est également vrai dans un plan. Par conséquent, s'il s'\(\vecs{F}\)agit d'un champ vectoriel dans un plan ou dans l'espace et que le domaine est simplement connecté, alors\(\vecs{F}\) est conservateur si et seulement si\(\text{curl}\, \vecs F = \vecs 0\).
Utilisez la boucle pour déterminer si elle\(\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle\) est conservatrice.
Solution
Notez que le domaine de\(\vecs{F}\)\(\mathbb{R}^3\) est entièrement connecté (Figure\(\PageIndex{7}\)). Par conséquent, nous pouvons tester si elle\(\vecs{F}\) est conservatrice en calculant sa courbure.
La boucle de\(\vecs{F}\) c'est
\[\left(\dfrac{\partial}{\partial y}xy - \dfrac{\partial}{\partial z} xz \right) \,\mathbf{\hat i} + \left(\dfrac{\partial}{\partial y}yz - \dfrac{\partial}{\partial z} xy \right) \,\mathbf{\hat j} + \left(\dfrac{\partial}{\partial y}xz - \dfrac{\partial}{\partial z} yz \right)\,\mathbf{\hat k}= (x - x)\,\mathbf{\hat i} + (y - y)\,\mathbf{\hat j} + (z - z)\,\mathbf{\hat k} = \vecs 0. \nonumber \]
Donc,\(\vecs{F}\) c'est conservateur.
Nous avons vu que la courbure d'un dégradé est nulle. Qu'est-ce que la divergence d'un gradient ? C'\(f\)est une fonction de deux variables, alors\(\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy}\). Nous abrégeons ce « produit à double point » en\(\vecs \nabla^2\). Cet opérateur est appelé opérateur de Laplace, et dans cette notation, l'équation de Laplace devient\(\vecs \nabla^2 f = 0\). Par conséquent, une fonction harmonique est une fonction qui devient nulle après avoir pris la divergence d'un gradient.
De même, si\(f\) c'est une fonction de trois variables alors
\[\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy} + f_{zz}. \nonumber \]
En utilisant cette notation, nous obtenons l'équation de Laplace pour les fonctions harmoniques de trois variables :
\[\vecs \nabla^2 f = 0. \nonumber \]
Les fonctions harmoniques apparaissent dans de nombreuses applications. Par exemple, la fonction potentielle d'un champ électrostatique dans une région de l'espace dépourvue de charge statique est harmonique.
Est-il possible qu'il\(f(x,y) = x^2 + x - y\) s'agisse de la fonction potentielle d'un champ électrostatique situé dans une région\(\mathbb{R}^2\) exempte de charge statique ?
Solution
Si\(f\) c'était une telle fonction potentielle,\(f\) elle serait harmonique. Notez cela\(f_{xx} = 2\) et\(f_{yy} = 0\), et ainsi de suite\(f_{xx} + f_{yy} \neq 0\). Par conséquent, n'\(f\)est pas harmonique et\(f\) ne peut pas représenter un potentiel électrostatique.
Est-il possible que la fonction\(f(x,y) = x^2 - y^2 + x\) soit la fonction potentielle d'un champ électrostatique situé dans une région\(\mathbb{R}^2\) exempte de charge statique ?
- Allusion
-
Déterminez si la fonction est harmonique.
- Réponse
-
Oui.
Concepts clés
- La divergence d'un champ vectoriel est une fonction scalaire. La divergence mesure le « débit sortant » d'un champ vectoriel. Si\(\vecs{v}\) est le champ de vitesse d'un fluide, alors la divergence d'\(\vecs{v}\)en un point est la sortie du fluide moins le débit entrant au point.
- La courbure d'un champ vectoriel est un champ vectoriel. La courbure d'un champ vectoriel en un point\(P\) mesure la tendance des particules\(P\) à tourner autour de l'axe qui pointe dans la direction de la courbure\(P\).
- Un champ vectoriel avec un domaine simplement connecté est conservateur si et seulement si sa courbure est nulle.
Équations clés
- Boucler
\[\vecs \nabla \times \vecs{F} = (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \nonumber \]
- divergence
\[\vecs \nabla \cdot \vecs{F} = P_x + Q_y + R_z\nonumber \]
- La divergence de la boucle est nulle
\[\vecs \nabla \cdot (\vecs \nabla \times \vecs F) = 0\nonumber \]
- La courbure d'un dégradé est le vecteur zéro
\[\vecs \nabla \times (\vecs \nabla f) = 0 \nonumber \]
Lexique
- boucle
- la boucle du champ vectoriel\(\vecs{F}=⟨P,Q,R⟩\), désignée\(\vecs ∇× \vecs{F}\) est le « déterminant » de la matrice\[\begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \] et est donnée par l'expression\((R_y−Q_z)\,\mathbf{\hat i} +(P_z−R_x)\,\mathbf{\hat j} +(Q_x−P_y)\,\mathbf{\hat k} \) ; elle mesure la tendance des particules à tourner autour de l'axe qui pointe dans la direction de la courbure au point
- divergence
- la divergence d'un champ vectoriel\(\vecs{F}=⟨P,Q,R⟩\), notée\(\vecs ∇× \vecs{F}\)\(P_x+Q_y+R_z\), est : elle mesure le « débit sortant » d'un champ vectoriel



L'une des applications de la divergence se trouve en physique, lorsque l'on travaille avec des champs magnétiques. Un champ magnétique est un champ vectoriel qui modélise l'influence des courants électriques et des matériaux magnétiques. Les physiciens utilisent la divergence dans la loi de Gauss pour le magnétisme, selon laquelle s'il s'\(\vecs{B}\)agit d'un champ magnétique, alors\(\vecs \nabla \cdot \vecs{B} = 0\) ; en d'autres termes, la divergence d'un champ magnétique est nulle.
Exemple\(\PageIndex{2}\): Determining Whether a Field Is Magnetic
Est-il possible que ce\(\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle \) soit un champ magnétique ?
Solution
Si elle\(\vecs{F}\) était magnétique, sa divergence serait nulle. La divergence de\(\vecs{F}\) est
\[\dfrac{\partial}{\partial x} (x^2y) + \dfrac{\partial}{\partial y} (y - xy^2) = 2 xy + 1 - 2 xy = 1 \nonumber \]
et\(\vecs{F}\) ne peut donc pas modéliser un champ magnétique (Figure\(\PageIndex{3}\)).