Skip to main content
Global

16,5E : Exercices pour la section 16.5

  1. Last updated
  2. Save as PDF
  • Page ID
    197888

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pour les exercices suivants, déterminez si l'énoncé est vrai ou faux.

    1. Si les fonctions de coordonnées de\(\vecs F : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) ont des dérivées partielles secondes continues,\(\text{curl} \, (\text{div} \,\vecs F)\) alors vaut zéro.

    2. \(\vecs\nabla \cdot (x \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z \,\mathbf{\hat k} ) = 1\).

    Réponse
    Faux

    3. Tous les champs vectoriels du formulaire\(\vecs F(x,y,z) = f(x)\,\mathbf{\hat i} + g(y)\,\mathbf{\hat j} + h(z)\,\mathbf{\hat k}\) sont conservateurs.

    4. Si\(\text{curl} \, \vecs F = \vecs 0\), alors\(\vecs F\) c'est conservateur.

    Réponse
    Vrai

    5. C'\(\vecs F\)est un champ vectoriel constant alors\(\text{div} \,\vecs F = 0\).

    6. C'\(\vecs F\)est un champ vectoriel constant alors\(\text{curl} \,\vecs F =\vecs 0\).

    Réponse
    Vrai

    Pour les exercices suivants, trouvez la boucle de\(\vecs F\).

    7. \(\vecs F(x,y,z) = xy^2z^4\,\mathbf{\hat i} + (2x^2y + z)\,\mathbf{\hat j} + y^3 z^2\,\mathbf{\hat k}\)

    8. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x\,\mathbf{\hat j} + (y + 2z)\,\mathbf{\hat k}\)

    Réponse
    \(\text{curl} \,\vecs F = \,\mathbf{\hat i} + x^2\,\mathbf{\hat j} + y^2\,\mathbf{\hat k}\)

    9. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z\,\mathbf{\hat j} + xe^{2z}\,\mathbf{\hat k}\)

    10. \(\vecs F(x,y,z) = x^2 yz\,\mathbf{\hat i} + xy^2 z\,\mathbf{\hat j} + xyz^2\,\mathbf{\hat k}\)

    Réponse
    \(\text{curl} \, \vecs F = (xz^2 - xy^2)\,\mathbf{\hat i} + (x^2 y - yz^2)\,\mathbf{\hat j} + (y^2z - x^2z)\,\mathbf{\hat k}\)

    11. \(\vecs F(x,y,z) = (x \, \cos y)\,\mathbf{\hat i} + xy^2\,\mathbf{\hat j}\)

    12. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z)\,\mathbf{\hat j} + (z - x)\,\mathbf{\hat k}\)

    Réponse
    \(\text{curl }\, \vecs F = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)

    13. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2 \,\mathbf{\hat j} + y^2z^3 \,\mathbf{\hat k}\)

    14. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz \,\mathbf{\hat j} + xz \,\mathbf{\hat k}\)

    Réponse
    \(\text{curl }\, \vecs F = - y\,\mathbf{\hat i} - z \,\mathbf{\hat j} - x \,\mathbf{\hat k}\)

    15. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)

    16. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\)pour les constantes\(a, \,b, \,c\).

    Réponse
    \(\text{curl }\, \vecs F = \vecs 0\)

    Pour les exercices suivants, trouvez la divergence de\(\vecs F\).

    17. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x \,\mathbf{\hat j} + (y + 2z) \,\mathbf{\hat k}\)

    18. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z \,\mathbf{\hat j} + xe^2 \,\mathbf{\hat k}\)

    Réponse
    \(\text{div}\,\vecs F = 3yz^2 + 2y \, \sin z + 2xe^{2z}\)

    19. \(\vecs{F}(x,y) = (\sin x)\,\mathbf{\hat i} + (\cos y) \,\mathbf{\hat j}\)

    20. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)

    Réponse
    \(\text{div}\,\vecs F = 2(x + y + z)\)

    21. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z) \,\mathbf{\hat j} + (z - x) \,\mathbf{\hat k}\)

    22. \(\vecs{F}(x,y) = \dfrac{x}{\sqrt{x^2+y^2}}\,\mathbf{\hat i} + \dfrac{y}{\sqrt{x^2+y^2}}\,\mathbf{\hat j}\)

    Réponse
    \(\text{div}\,\vecs F = \dfrac{1}{\sqrt{x^2+y^2}}\)

    23. \(\vecs{F}(x,y) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j}\)

    24. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\)pour les constantes\(a, \,b, \,c\).

    Réponse
    \(\text{div}\,\vecs F = a + b\)

    25. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2\,\mathbf{\hat j} + y^2z^3\,\mathbf{\hat k}\)

    26. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\)

    Réponse
    \(\text{div}\,\vecs F = x + y + z\)

    Pour les exercices 27 et 28, déterminez si chacune des fonctions scalaires données est harmonique.

    27. \(u(x,y,z) = e^{-x} (\cos y - \sin y)\)

    28. \(w(x,y,z) = (x^2 + y^2 + z^2)^{-1/2}\)

    Réponse
    harmonique

    29. Si\(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) et\(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), trouvez\(\text{curl} \, (\vecs F \times \vecs G)\).

    30. Si\(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) et\(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), trouvez\(\text{div} \, (\vecs F \times \vecs G)\).

    Réponse
    \(\text{div} \, (\vecs F \times \vecs G) = 2z + 3x\)

    31. \(\text{div} \,\vecs F\)Trouve, étant donné cela\(\vecs F = \vecs \nabla f\), où\(f(x,y,z) = xy^3z^2\).

    32. Détermine la divergence de\(\vecs F\) pour le champ vectoriel\(\vecs F(x,y,z) = (y^2 + z^2) (x + y) \,\mathbf{\hat i} + (z^2 + x^2)(y + z) \,\mathbf{\hat j} + (x^2 + y^2)(z + x) \,\mathbf{\hat k}\).

    Réponse
    \(\text{div}\,\vecs F = 2r^2\)

    33. Détermine la divergence de\(\vecs F\) pour le champ vectoriel\(\vecs F(x,y,z) = f_1(y,z)\,\mathbf{\hat i} + f_2 (x,z) \,\mathbf{\hat j} + f_3 (x,y) \,\mathbf{\hat k}\).

    Pour les exercices 34 à 36, utilisez\(r = |\vecs r|\) et\(\vecs r(x,y,z) = \langle x,y,z\rangle\).

    34. Trouvez le\(\text{curl} \, \vecs r\)

    Réponse
    \(\text{curl} \, \vecs r = \vecs 0\)

    35. Trouvez le\(\text{curl}\, \dfrac{\vecs r}{r}\).

    36. Trouvez le\(\text{curl}\, \dfrac{\vecs r}{r^3}\).

    Réponse
    \(\text{curl}\, \dfrac{\vecs r}{r^3} = \vecs 0\)

    37. \(\vecs{F}(x,y) = \dfrac{-y\,\mathbf{\hat i}+x\,\mathbf{\hat j}}{x^2+y^2}\)Let, où\(\vecs F\) est défini sur\(\big\{(x,y) \in \mathbb{R} | (x,y) \neq (0,0) \big\}\). Trouvez\(\text{curl}\, \vecs F\).

    Pour les exercices suivants, utilisez un système d'algèbre informatique pour trouver la courbure des champs vectoriels donnés.

    38. [T]\(\vecs F(x,y,z) = \arctan \left(\dfrac{x}{y}\right)\,\mathbf{\hat i} + \ln \sqrt{x^2 + y^2} \,\mathbf{\hat j}+ \,\mathbf{\hat k}\)

    Réponse
    \(\text{curl }\, \vecs F = \dfrac{2x}{x^2+y^2}\,\mathbf{\hat k}\)

    39. [T]\(\vecs F(x,y,z) = \sin (x - y)\,\mathbf{\hat i} + \sin (y - z) \,\mathbf{\hat j} + \sin (z - x) \,\mathbf{\hat k}\)

    Pour les exercices suivants, trouvez la divergence de\(\vecs F\) au point donné.

    40. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)à\((2, -1, 3)\)

    Réponse
    \(\text{div}\,\vecs F = 0\)

    41. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\)à\((1, 2, 3)\)

    42. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\)à\((3, 2, 0)\)

    Réponse
    \(\text{div}\,\vecs F = 2 - 2e^{-6}\)

    43. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\)à\((1, 2, 1)\)

    44. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \)à\((0, 0, 3)\)

    Réponse
    \(\text{div}\,\vecs F = 0\)

    Pour les exercices 45 à 49, trouvez la boucle de\(\vecs F\) l'endroit indiqué.

    45. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)à\((2, -1, 3)\)

    46. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\)à\((1, 2, 3)\)

    Réponse
    \(\text{curl }\, \vecs F = \mathbf{\hat j} - 3\,\mathbf{\hat k}\)

    47. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\)à\((3, 2, 0)\)

    48. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\)à\((1, 2, 1)\)

    Réponse
    \(\text{curl }\, \vecs F = 2\,\mathbf{\hat j} - \,\mathbf{\hat k}\)

    49. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \)à\((0, 0, 3)\)

    50. Laissez\(\vecs F(x,y,z) = (3x^2 y + az) \,\mathbf{\hat i} + x^3\,\mathbf{\hat j} + (3x + 3z^2)\,\mathbf{\hat k}\). Pour quelle valeur de\(a\) est\(\vecs F\) conservatrice ?

    Réponse
    \(a = 3\)

    51. Le champ vectoriel étant donné\(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle -y,x\rangle\) sur le domaine\(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}} = \big\{(x,y) \in \mathbb{R}^2 |(x,y) \neq (0,0) \big\}\), est-ce\(\vecs F\) prudent ?

    52. Le champ vectoriel étant donné\(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle x,y\rangle\) sur le domaine\(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}}\), est-ce\(\vecs F\) prudent ?

    Réponse
    \(\vecs F\)est conservateur.

    53. Trouvez le travail effectué par champ\(\vecs{F}(x,y) = e^{-y}\,\mathbf{\hat i} - xe^{-y}\,\mathbf{\hat j}\) de force pour déplacer un objet de\(P(0, 1)\) à\(Q(2, 0)\). Le champ de force est-il conservateur ?

    54. Calculez la divergence\(\vecs F(x,y,z) = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\)

    Réponse
    \(\text{div}\,\vecs F = \cosh x + \sinh y - xy\)

    55. Calculer\(\text{curl }\, \vecs F = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\).

    Pour les exercices suivants, considérez un corps rigide qui tourne autour de l'\(x\)axe Y dans le sens antihoraire avec une vitesse angulaire constante\(\vecs \omega = \langle a,b,c \rangle\). S'il s'\(P\)agit d'un point du corps situé à\(\vecs r = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\), la vitesse à\(P\) est donnée par un champ vectoriel\(\vecs F = \vecs \omega \times \vecs r\).

    . The object is roughly a sphere with pointed ends on the x axis, which cuts it in half. An arrow r is drawn from (0,0,0) to P(x,y,z) and down from P(x,y,z) to the x axis." data-type="media" id="fs-id1167793480282">Schéma tridimensionnel d'un objet tournant autour de l'axe x dans le sens antihoraire avec une vitesse angulaire constante w = <a, b, c. L'objet est à peu près une sphère dont les extrémités sont pointues sur l'axe x, ce qui la coupe en deux. Une flèche r est tracée de (0,0,0) à P (x, y, z) et vers le bas de P (x, y, z) jusqu'à l'axe x." src="https://math.libretexts.org/@api/dek...16_05_201.jpeg">

    56. Express\(\vecs F\) in terms of \(\,\mathbf{\hat i},\;\,\mathbf{\hat j},\) and \(\,\mathbf{\hat k}\) vectors.

    Answer
    \(\vecs F = (bz - cy)\,\mathbf{\hat i}+(cx - az)\,\mathbf{\hat j} + (ay - bx)\,\mathbf{\hat k}\)

    57. Find \(\text{div} \, F\).

    58. Find \(\text{curl} \, F\)

    Answer
    \(\text{curl }\, \vecs F = 2\vecs\omega\)

    In the following exercises, suppose that \(\vecs \nabla \cdot \vecs F = 0\) and \(\vecs \nabla \cdot \vecs G = 0\).

    59. Does \(\vecs F + \vecs G\) necessarily have zero divergence?

    60. Does \(\vecs F \times \vecs G\) necessarily have zero divergence?

    Answer
    \(\vecs F \times \vecs G\) does not have zero divergence.

    In the following exercises, suppose a solid object in \(\mathbb{R}^3\) has a temperature distribution given by \(T(x,y,z)\). The heat flow vector field in the object is \(\vecs F = - k \vecs \nabla T\), where \(k > 0\) is a property of the material. The heat flow vector points in the direction opposite to that of the gradient, which is the direction of greatest temperature decrease. The divergence of the heat flow vector is \(\vecs \nabla \cdot \vecs F = -k \vecs \nabla \cdot \vecs \nabla T = - k \vecs \nabla^2 T\).

    61. Compute the heat flow vector field.

    62. Compute the divergence.

    Answer
    \(\vecs \nabla \cdot \vecs F = -200 k [1 + 2(x^2 + y^2 + z^2)] e^{-x^2+y^2+z^2}\)

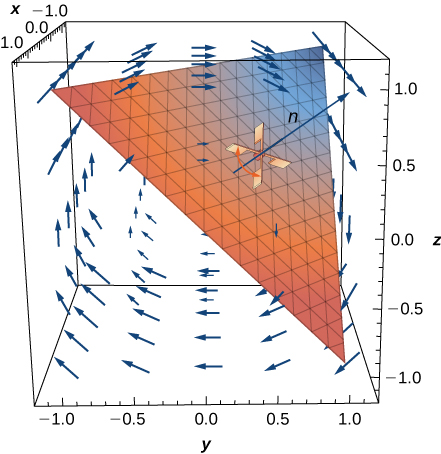
    63. [T] Consider rotational velocity field \(\vecs v = \langle 0,10z, -10y \rangle\). If a paddlewheel is placed in plane \(x + y + z = 1\) with its axis normal to this plane, using a computer algebra system, calculate how fast the paddlewheel spins in revolutions per unit time.

    A three dimensional diagram of a rotational velocity field. The arrows are showing a rotation in a clockwise manner. A paddlewheel is shown in plan x + y + z = 1 with n extended out perpendicular to the plane.