16.6 : Intégrales de surface
- Page ID
- 197805
- Trouvez les représentations paramétriques d'un cylindre, d'un cône et d'une sphère.
- Décrivez l'intégrale de surface d'une fonction à valeur scalaire sur une surface paramétrique.
- Utilisez une intégrale de surface pour calculer l'aire d'une surface donnée.
- Expliquez la signification d'une surface orientée, en donnant un exemple.
- Décrivez l'intégrale de surface d'un champ vectoriel.
- Utilisez des intégrales de surface pour résoudre les problèmes appliqués.
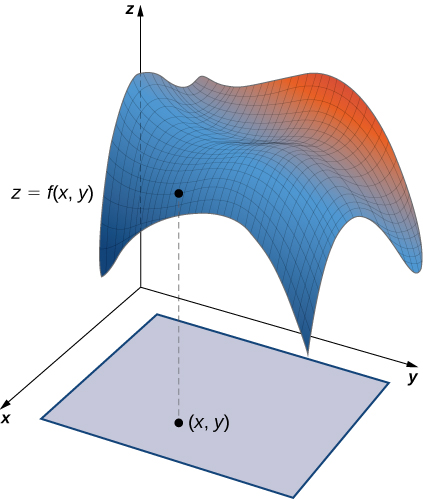
Nous avons vu qu'une intégrale linéaire est une intégrale au-dessus d'une trajectoire dans un plan ou dans l'espace. Cependant, si nous souhaitons intégrer sur une surface (un objet bidimensionnel) plutôt que sur un chemin (un objet unidimensionnel) dans l'espace, nous avons besoin d'un nouveau type d'intégrale capable de gérer l'intégration sur des objets de dimensions supérieures. Nous pouvons étendre le concept d'une ligne intégrale à une intégrale de surface pour nous permettre de réaliser cette intégration.
Les intégrales de surface sont importantes pour les mêmes raisons que les intégrales linéaires. Ils ont de nombreuses applications en physique et en génie, et ils nous permettent de développer des versions dimensionnelles supérieures du théorème fondamental du calcul. En particulier, les intégrales de surface nous permettent de généraliser le théorème de Green à des dimensions plus élevées, et elles apparaissent dans certains théorèmes importants que nous aborderons dans les sections suivantes.
Surfaces paramétriques
Une intégrale de surface est similaire à une intégrale linéaire, sauf que l'intégration se fait sur une surface plutôt que sur une trajectoire. En ce sens, les intégrales de surface élargissent notre étude des intégrales linéaires. Tout comme pour les intégrales linéaires, il existe deux types d'intégrales de surface : une intégrale de surface d'une fonction à valeur scalaire et une intégrale de surface d'un champ vectoriel.
Cependant, avant de pouvoir intégrer sur une surface, nous devons prendre en compte la surface elle-même. Rappelons que pour calculer une intégrale scalaire ou vectorielle sur une courbe\(C\), nous devons d'abord paramétrer\(C\). De la même manière, pour calculer une surface intégrale sur la surface\(S\), il faut paramétrer\(S\). C'est-à-dire que nous avons besoin d'un concept fonctionnel d'une surface paramétrée (ou d'une surface paramétrique), de la même manière que nous avons déjà un concept de courbe paramétrée.
Une surface paramétrée est donnée par une description de la forme
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
Notez que ce paramétrage implique deux paramètres\(u\) et\(v\), comme une surface est bidimensionnelle, deux variables sont donc nécessaires pour tracer la surface. Les paramètres\(u\) et\(v\) varient sur une région appelée domaine des paramètres, ou espace des paramètres, c'est-à-dire l'ensemble des points du\(uv\) plan dans lesquels il est possible de les remplacer\(\vecs r\). Chaque choix de\(u\) et\(v\) dans le domaine des paramètres donne un point sur la surface, tout comme chaque choix d'un paramètre\(t\) donne un point sur une courbe paramétrée. La surface entière est créée en faisant tous les choix possibles pour\(u\) et\(v\) sur le domaine des paramètres.
Compte tenu d'un paramétrage de la surface
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
le domaine paramétrique de la paramétrisation est l'ensemble des points du\(uv\) plan qui peuvent être remplacés par\(\vecs r\).
Décrire la surface\(S\) paramétrée par
\[\vecs{r}(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, -\infty < u < \infty, \, -\infty < v < \infty. \nonumber \]
Solution
Pour avoir une idée de la forme de la surface, nous tracons d'abord quelques points. Comme le domaine des paramètres est complet\(\mathbb{R}^2\), nous pouvons choisir n'importe quelle valeur pour u et v et tracer le point correspondant. Si\(u = v = 0\), alors\(\vecs r(0,0) = \langle 1,0,0 \rangle\), le point (1, 0, 0) est activé\(S\). De même, les points\(\vecs r(\pi, 2) = (-1,0,2)\) et\(\vecs r \left(\dfrac{\pi}{2}, 4\right) = (0,1,4)\) les points sont activés\(S\).
Bien que le traçage des points puisse nous donner une idée de la forme de la surface, nous avons généralement besoin de quelques points pour voir la forme. Comme il faut du temps pour tracer des dizaines ou des centaines de points, nous utilisons une autre stratégie. Pour les visualiser\(S\), nous visualisons deux familles de courbes qui se trouvent sur elles\(S\). Dans la première famille de courbes, nous maintenons\(u\) une constante ; dans la seconde famille de courbes, nous maintenons\(v\) une constante. Cela nous permet de construire un « squelette » de la surface et de se faire une idée de sa forme.
- Supposons que ce\(u\) soit une constante\(K\). La courbe tracée par le paramétrage est alors\(\langle \cos K, \, \sin K, \, v \rangle \), ce qui donne une ligne verticale passant par un point\((\cos K, \sin K, v \rangle\) dans le\(xy\) plan.
- Supposons que ce\(v\) soit une constante\(K\). La courbe tracée par le paramétrage est alors\(\langle \cos u, \, \sin u, \, K \rangle \), ce qui donne un cercle dans un plan\(z = K\) de rayon 1 et de centre\((0, 0, K)\).
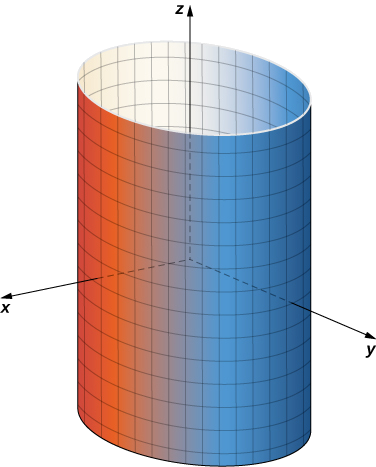
Si elle\(u\) est maintenue constante, alors nous obtenons des lignes verticales ; si elle\(v\) est maintenue constante, alors nous obtenons des cercles de rayon 1 centrés autour de la ligne verticale qui passe par l'origine. La surface tracée par le paramétrage est donc cylindrique\(x^2 + y^2 = 1\) (Figure\(\PageIndex{1}\)).
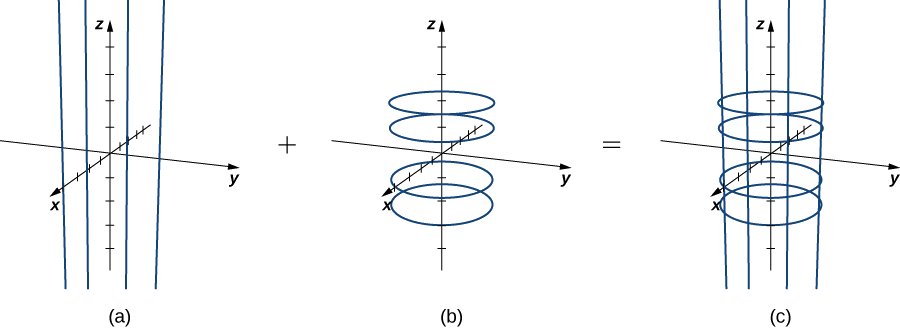
Remarquez que si\(x = \cos u\) et alors\(y = \sin u\)\(x^2 + y^2 = 1\), les points en provenance de S se trouvent effectivement sur le cylindre. Inversement, chaque point du cylindre est contenu dans un cercle\(\langle \cos u, \, \sin u, \, k \rangle \) pour certains\(k\), et donc chaque point du cylindre est contenu dans la surface paramétrée (Figure\(\PageIndex{2}\)).
Analyse
Notez que si nous changeons le domaine des paramètres, nous pourrions obtenir une surface différente. Par exemple, si nous limitions le domaine à\(0 \leq u \leq \pi, \, -\infty < v < 6\), la surface serait un demi-cylindre de hauteur 6.
Décrire la surface avec paramétrage
\[\vecs{r} (u,v) = \langle 2 \, \cos u, \, 2 \, \sin u, \, v \rangle, \, 0 \leq u \leq 2\pi, \, -\infty < v < \infty \nonumber \]
- Allusion
-
Maintenez la\(v\) constante\(u\) et voyez le type de courbes qui en résultent.
- Réponse
-
cylindre\(x^2 + y^2 = 4\)
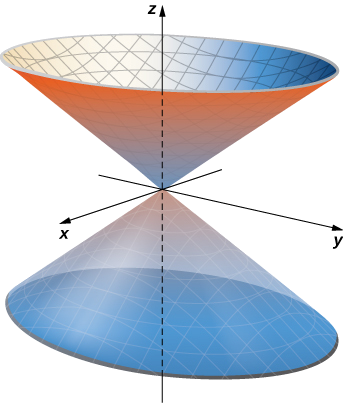
Donnez un paramétrage du cône\(x^2 + y^2 = z^2\) situé sur ou au-dessus du plan\(z = -2\).
Solution
La section transversale horizontale du cône en hauteur\(z = u\) est circulaire\(x^2 + y^2 = u^2\). Par conséquent, un point situé en hauteur sur le cône\(u\) possède\((u \, \cos v, \, u \, \sin v, \, u)\) des coordonnées d'angle\(v\). Par conséquent, un paramétrage du cône est\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle \). Comme nous ne nous intéressons pas à l'ensemble du cône, mais uniquement à la partie située sur ou au-dessus du plan\(z = -2\), le domaine des paramètres est donné par\(-2 < u < \infty, \, 0 \leq v < 2\pi\) (Figure\(\PageIndex{4}\)).
Donnez un paramétrage pour la portion de cône\(x^2 + y^2 = z^2\) située dans le premier octant.
- Allusion
-
Considérez le domaine des paramètres de cette surface.
- Réponse
-
\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 < u < \infty, \, 0 \leq v < \dfrac{\pi}{2}\)
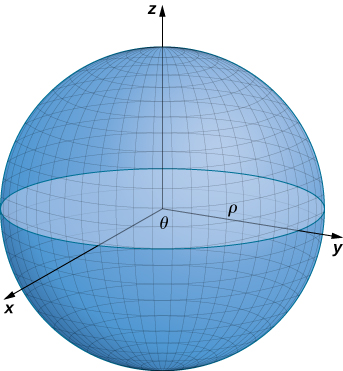
Nous avons discuté des paramétrisations de différentes surfaces, mais deux types importants de surfaces nécessitent une discussion séparée : les sphères et les graphes de fonctions à deux variables. Pour paramétrer une sphère, il est plus facile d'utiliser des coordonnées sphériques. La sphère de rayon\(\rho\) centrée à l'origine est donnée par le paramétrage
\(\vecs r(\phi,\theta) = \langle \rho \, \cos \theta \, \sin \phi, \, \rho \, \sin \theta \, \sin \phi, \, \rho \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi.\)
L'idée de ce paramétrage est qu'en\(\phi\) balayant vers le bas à partir de\(z\) l'axe positif, un cercle de rayon\(\rho \, \sin \phi\) est tracé en laissant\(\theta\) courir de 0 à\(2\pi\). Pour voir cela,\(\phi\) soyons corrigés. Alors
\ [\ begin {align*} x^2 + y^2 &= (\ rho \, \ cos \ thêta \, \ sin \ phi) ^2 + (\ rho \, \ sin \ thêta \, \ sin \ phi) ^2 \ \ [4 points]
&= \ rho^2 \ sin^2 \ phi (\ cos^2 \ thêta + \ sin^2 \ thêta) \ [4 points]
&= \ rho^2 \, \ sin^2 \ phi \ \ [4 points]
&= (\ rho \, \ sin \ phi) ^2. \ end {align*} \]
Cela donne le cercle souhaité (Figure\(\PageIndex{5}\)).
Enfin, pour paramétrer le graphe d'une fonction à deux variables, on laisse d'abord\(z = f(x,y)\) être une fonction de deux variables. Le paramétrage le plus simple du graphe de\(f\) est\(\vecs r(x,y) = \langle x,y,f(x,y) \rangle\) où\(x\) et\(y\) varie sur le domaine de\(f\) (Figure\(\PageIndex{6}\)). Par exemple, le graphe de\(f(x,y) = x^2 y\) peut être paramétré par\(\vecs r(x,y) = \langle x,y,x^2y \rangle\), où les paramètres\(x\) et\(y\) varient sur le domaine de\(f\). Si nous ne nous intéressons qu'à une partie du\(f\) graphe, par exemple la partie du graphique au-dessus d'un rectangle\([ 1,3] \times [2,5]\), nous pouvons restreindre le domaine des paramètres pour donner cette partie de la surface :
\[\vecs r(x,y) = \langle x,y,x^2y \rangle, \, 1 \leq x \leq 3, \, 2 \leq y \leq 5. \nonumber \]
De même, s'il s'\(S\)agit d'une surface donnée par une équation\(x = g(y,z)\) ou une équation\(y = h(x,z)\), alors une paramétrisation de\(S\) est\(\vecs r(y,z) = \langle g(y,z), \, y,z\rangle\) ou\(\vecs r(x,z) = \langle x,h(x,z), z\rangle\), respectivement. Par exemple, le graphe du paraboloïde\(2y = x^2 + z^2\) peut être paramétré par\(\vecs r(x,y) = \left\langle x, \dfrac{x^2+z^2}{2}, z \right\rangle, \, 0 \leq x < \infty, \, 0 \leq z < \infty\). Notez que nous n'avons pas besoin de varier sur l'ensemble du domaine\(y\) car\(x\) et\(z\) sont au carré.
Généralisons maintenant les notions de douceur et de régularité à une surface paramétrique. N'oubliez pas que le paramétrage de la courbe\(\vecs r(t), \, a \leq t \leq b\) est régulier (ou fluide), même s'il\(\vecs r'(t) \neq \vecs 0\) est\(t\) intégré\([a,b]\). Pour une courbe, cette condition garantit que l'image de\(\vecs r\) vraiment est une courbe, et pas simplement un point. Par exemple, considérez le paramétrage des courbes\(\vecs r(t) = \langle 1,2\rangle, \, 0 \leq t \leq 5\). L'image de ce paramétrage est simplement ponctuelle\((1,2)\), ce qui n'est pas une courbe. Remarquez également que\(\vecs r'(t) = \vecs 0\). Le fait que la dérivée soit le vecteur zéro indique que nous ne sommes pas réellement en train de regarder une courbe.
De même, nous aimerions avoir une notion de régularité (ou de douceur) pour les surfaces afin qu'un paramétrage de surface trace réellement une surface. Pour motiver la définition de la régularité d'un paramétrage de surface, considérez le paramétrage
\[\vecs r(u,v) = \langle 0, \, \cos v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq \pi. \nonumber \]
Bien que ce paramétrage semble être le paramétrage d'une surface, notez que l'image est en fait une ligne (Figure\(\PageIndex{7}\)). Comment éviter de tels paramétrages ? Des paramétrages qui ne donnent pas de surface réelle ? Notez que\(\vecs r_u = \langle 0,0,0 \rangle\) et\(\vecs r_v = \langle 0, -\sin v, 0\rangle\), et le produit croisé correspondant est zéro. L'analogue de la condition\(\vecs r'(t) = \vecs 0\) est qu'il n'\(\vecs r_u \times \vecs r_v\)est pas égal à zéro pour un point\((u,v)\) dans le domaine des paramètres, ce qui correspond à un paramétrage normal.
Le paramétrage\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) est un paramétrage normal s'il n'\(\vecs r_u \times \vecs r_v\)est pas égal à zéro pour un point\((u,v)\) dans le domaine du paramètre.
Si le paramétrage\(\vec{r}\) est régulier, alors l'image de\(\vec{r}\) est un objet bidimensionnel, comme devrait l'être une surface. Tout au long de ce chapitre, les\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) paramétrages sont supposés être réguliers.
Rappelez-vous que le paramétrage de la courbe\(\vecs r(t), \, a \leq t \leq b\) est fluide s'il\(\vecs r'(t)\) est continu et\(\vecs r'(t) \neq \vecs 0\)\(t\) intégré\([a,b]\). De manière informelle, le paramétrage d'une courbe est fluide si la courbe résultante ne présente pas d'angles vifs. La définition d'un paramétrage de surface lisse est similaire. De manière informelle, le paramétrage d'une surface est fluide si la surface obtenue ne présente pas d'angles vifs.
Un paramétrage de surface\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) est fluide si le vecteur n'\(\vecs r_u \times \vecs r_v\)est pas nul pour n'importe quel choix de\(u\) et\(v\) dans le domaine des paramètres.
Une surface peut également être lisse par morceaux si elle possède des faces lisses mais aussi des emplacements où les dérivées directionnelles n'existent pas.
Laquelle des figures de la figure\(\PageIndex{8}\) est lisse ?

Solution
La surface de la figure\(\PageIndex{8a}\) peut être paramétrée par
\[\vecs r(u,v) = \langle (2 + \cos v) \cos u, \, (2 + \cos v) \sin u, \, \sin v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v < 2\pi \nonumber \]
(nous pouvons utiliser la technologie pour vérifier). Notez que les vecteurs
\[\vecs r_u = \langle - (2 + \cos v)\sin u, \, (2 + \cos v) \cos u, 0 \rangle \nonumber \]
et
\[\vecs r_v = \langle -\sin v \, \cos u, \, - \sin v \, \sin u, \, \cos v \rangle \nonumber \]
existent pour n'importe quel choix de\(u\) et\(v\) dans le domaine des paramètres, et
\[ \begin{align*} \vecs r_u \times \vecs r_v &= \begin{vmatrix} \mathbf{\hat{i}}& \mathbf{\hat{j}}& \mathbf{\hat{k}} \\ -(2 + \cos v)\sin u & (2 + \cos v)\cos u & 0\\ -\sin v \, \cos u & - \sin v \, \sin u & \cos v \end{vmatrix} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [2 + \cos v) \sin u \, \cos v] \mathbf{\hat{j}} + [(2 + \cos v)\sin v \, \sin^2 u + (2 + \cos v) \sin v \, \cos^2 u]\mathbf{\hat{k}} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [(2 + \cos v) \sin u \, \cos v]\mathbf{\hat{j}} + [(2 + \cos v)\sin v ] \mathbf{\hat{k}}. \end{align*}\]
La\(\mathbf{\hat{k}}\) composante de ce vecteur est nulle uniquement si\(v = 0\) ou\(v = \pi\). Si\(v = 0\) c'est le cas\(v = \pi\), les seuls choix pour\(u\) lesquels la\(\mathbf{\hat{j}}\) composante est nulle sont\(u = 0\) ou\(u = \pi\). Mais, ces choix de ne\(u\) font pas de la\(\mathbf{\hat{i}}\) composante zéro. Par conséquent, n'\(\vecs r_u \times \vecs r_v\)est pas nul pour tout choix de\(u\) et\(v\) dans le domaine des paramètres, et le paramétrage est fluide. Notez que la surface correspondante n'a pas d'angles vifs.
Dans la pyramide de la figure\(\PageIndex{8b}\), la netteté des angles garantit l'absence de dérivées directionnelles à ces emplacements. Par conséquent, la pyramide n'a pas de paramétrage fluide. Cependant, la pyramide se compose de quatre faces lisses, et cette surface est donc lisse par morceaux.
Le paramétrage de la surface est-il\(\vecs r(u,v) = \langle u^{2v}, v + 1, \, \sin u \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3\) fluide ?
- Allusion
-
Examinez le produit croisé\(\vecs r_u \times \vecs r_v\).
- Réponse
-
Oui
Surface d'une surface paramétrique
Notre objectif est de définir une intégrale de surface et, dans un premier temps, nous avons examiné comment paramétrer une surface. La deuxième étape consiste à définir la surface d'une surface paramétrique. La notation nécessaire pour développer cette définition est utilisée dans la suite de ce chapitre.
\(S\)Soit une surface paramétrée\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) sur un domaine de paramètres\(D\). Nous supposons ici et partout que le paramétrage de la surface\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) est continuellement dérivable, c'est-à-dire que chaque fonction constitutive possède des dérivées partielles continues. Supposons, pour des raisons de simplicité, qu'il\(D\) s'agit d'un rectangle (bien que le matériel suivant puisse être étendu pour gérer des domaines de paramètres non rectangulaires). Divisez\(D\) le rectangle en\(D_{ij}\) sous-rectangles de largeur horizontale\(\Delta u\) et de longueur verticale\(\Delta v\). Supposons que i soit compris entre 1 et m et que j soit compris entre 1 et n, de sorte qu'il\(D\) soit subdivisé en mn rectangles. Cette division\(D\) en sous-rectangles donne une division correspondante de la surface\(S\) en morceaux\(S_{ij}\). Choisissez un point\(P_{ij}\) dans chaque pièce\(S_{ij}\). Le point\(P_{ij}\) correspond\((u_i, v_j)\) au point du domaine des paramètres.
Notez que nous pouvons former une grille avec des lignes parallèles à l'\(u\)axe -et à l'\(v\)axe -dans le\(uv\) plan. Ces lignes de grille correspondent à un ensemble de courbes de grille sur une surface\(S\) paramétrée par\(\vecs r(u,v)\). Sans perte de généralité, nous supposons qu'il\(P_{ij}\) est situé au coin de deux courbes de la grille, comme dans la Figure\(\PageIndex{9}\). Si nous considérons qu'il s'agit d'une cartographie du\(uv\) plan à\(\mathbb{R}^3\), les courbes de la grille sont l'image des lignes de la grille situées en dessous\(\vecs r\).\(\vecs r\) Pour être précis, considérez les lignes de la grille qui passent par le point\((u_i, v_j)\). Une ligne est donnée par\(x = u_i, \, y = v\) ; l'autre est donnée par\(x = u, \, y = v_j\). Dans la première ligne de la grille, la composante horizontale est maintenue constante, ce qui produit une ligne verticale traversante\((u_i, v_j)\). Dans la deuxième ligne de la grille, la composante verticale est maintenue constante, ce qui produit une ligne horizontale traversante\((u_i, v_j)\). Les courbes de la grille correspondantes sont\(\vecs r(u_i, v)\)\((u, v_j)\) et ces courbes se croisent au point\(P_{ij}\).
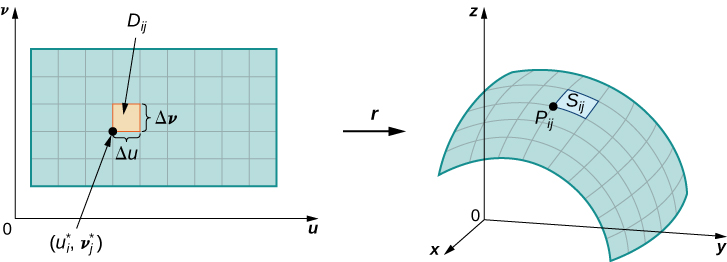
Considérons maintenant les vecteurs tangents à ces courbes de la grille. Pour une courbe de grille\(\vecs r(u_i,v)\), le vecteur tangent à\(P_{ij}\) est
\[\vecs t_v (P_{ij}) = \vecs r_v (u_i,v_j) = \langle x_v (u_i,v_j), \, y_v(u_i,v_j), \, z_v (u_i,v_j) \rangle. \nonumber \]
Pour une courbe de grille\(\vecs r(u, v_j)\), le vecteur tangent à\(P_{ij}\) est
\[\vecs t_u (P_{ij}) = \vecs r_u (u_i,v_j) = \langle x_u (u_i,v_j), \, y_u(u_i,v_j), \, z_u (u_i,v_j) \rangle. \nonumber \]
Si le vecteur\(\vecs N = \vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})\) existe et n'est pas nul, alors le plan tangent\(P_{ij}\) existe (Figure\(\PageIndex{10}\)). Si la pièce\(S_{ij}\) est suffisamment petite, le plan tangent au point\(P_{ij}\) est une bonne approximation de la pièce\(S_{ij}\).
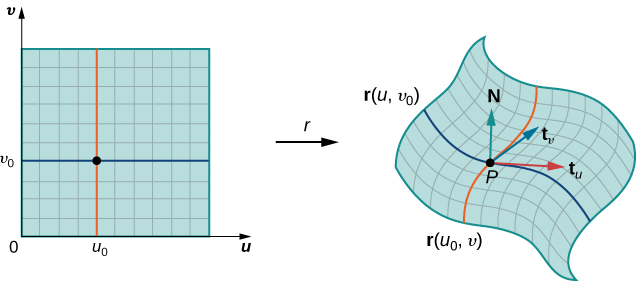
Le plan tangent at\(P_{ij}\) contient des vecteurs\(\vecs t_u(P_{ij})\)\(\vecs t_v(P_{ij})\) et donc le parallélogramme parcouru par\(\vecs t_u(P_{ij})\) et\(\vecs t_v(P_{ij})\) se trouve dans le plan tangent. Puisque le rectangle d'origine dans le\(uv\) plan -correspondant\(S_{ij}\) a une largeur\(\Delta u\) et une longueur\(\Delta v\), le parallélogramme que nous utilisons pour approximer\(S_{ij}\) est le parallélogramme parcouru par\(\Delta u \vecs t_u(P_{ij})\) et\(\Delta v \vecs t_v(P_{ij})\). En d'autres termes, nous redimensionnons les vecteurs tangents selon les constantes\(\Delta u\) et\(\Delta v\) pour qu'ils correspondent à l'échelle de la division initiale des rectangles dans le domaine des paramètres. Par conséquent, l'aire du parallélogramme utilisée pour approximer l'aire de\(S_{ij}\) est
\[\Delta S_{ij} \approx ||(\Delta u \vecs t_u (P_{ij})) \times (\Delta v \vecs t_v (P_{ij})) || = ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij}) || \Delta u \,\Delta v. \nonumber \]
La variation du point\(P_{ij}\) sur toutes les pièces\(S_{ij}\) et l'approximation précédente conduisent à la définition suivante de la surface d'une surface paramétrique (Figure\(\PageIndex{11}\)).
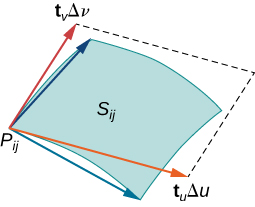
Supposons\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) que le domaine des paramètres\(D\) soit un paramétrage fluide de la surface\(S\). En outre, supposons que cela ne\(S\) soit tracé qu'une seule fois,\((u,v)\) selon les variations\(D\). La superficie de\(S\) est
\[\iint_D ||\vecs t_u \times \vecs t_v || \,dA, \label{equation1} \]
où\(\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\)
et
\[\vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Calculez la surface latérale (l'aire du « côté », base non comprise) du cône circulaire droit de hauteur h et de rayon r.
Solution
Avant de calculer la surface de ce cône à l'aide de l'équation \ ref {equation1}, nous avons besoin d'un paramétrage. Nous supposons que ce cône se trouve\(\mathbb{R}^3\) à l'intérieur et que son sommet est à l'origine (Figure\(\PageIndex{12}\)). Pour obtenir un paramétrage,\(\alpha\) soit l'angle qui est balayé en commençant par l'axe z positif et en finissant par le cône, et let\(k = \tan \alpha\). Pour une valeur de hauteur\(0 \leq v \leq h\) égale\(v\) à, le rayon du cercle formé en coupant le cône avec le plan\(z = v\) est de\(kv\). Par conséquent, un paramétrage de ce cône est
\[\vecs s(u,v) = \langle kv \, \cos u, \, kv \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h. \nonumber \]
L'idée qui sous-tend ce paramétrage est que pour une\(v\) valeur fixe, le cercle balayé en laissant\(u\) varier est le cercle en hauteur\(v\) et en rayon\(kv\). Au fur et à mesure qu'il\(v\) augmente, le paramétrage balaie une « pile » de cercles, ce qui donne le cône souhaité.
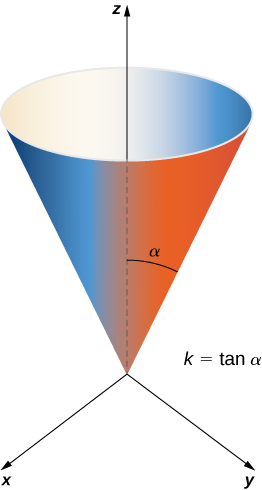
Avec un paramétrage en main, nous pouvons calculer la surface du cône à l'aide de l'équation \ ref {equation1}. Les vecteurs tangents sont\(\vecs t_u = \langle - kv \, \sin u, \, kv \, \cos u, \, 0 \rangle\) et\(\vecs t_v = \langle k \, \cos u, \, k \, \sin u, \, 1 \rangle\). Par conséquent,
\[ \begin{align*} \vecs t_u \times \vecs t_v &= \begin{vmatrix} \mathbf{\hat{i}} & \mathbf{\hat{j}} & \mathbf{\hat{k}} \\ -kv \sin u & kv \cos u & 0 \\ k \cos u & k \sin u & 1 \end{vmatrix} \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \, \sin^2 u - k^2 v \, \cos^2 u \rangle \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, - k^2 v \rangle. \end{align*}\]
L'amplitude de ce vecteur est
\[ \begin{align*} ||\langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \rangle || &= \sqrt{k^2 v^2 \cos^2 u + k^2 v^2 \sin^2 u + k^4v^2} \\[4pt] &= \sqrt{k^2v^2 + k^4v^2} \\[4pt] &= kv\sqrt{1 + k^2}. \end{align*}\]
Par l'équation \ ref {equation1}, la surface du cône est
\[ \begin{align*}\iint_D ||\vecs t_u \times \vecs t_v|| \, dA &= \int_0^h \int_0^{2\pi} kv \sqrt{1 + k^2} \,du\, dv \\[4pt] &= 2\pi k \sqrt{1 + k^2} \int_0^h v \,dv \\[4pt] &= 2 \pi k \sqrt{1 + k^2} \left[\dfrac{v^2}{2}\right]_0^h \\[4pt] \\[4pt] &= \pi k h^2 \sqrt{1 + k^2}. \end{align*}\]
Depuis\(k = \tan \alpha = r/h\),
\[ \begin{align*} \pi k h^2 \sqrt{1 + k^2} &= \pi \dfrac{r}{h}h^2 \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] &= \pi r h \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] \\[4pt] &= \pi r \sqrt{h^2 + h^2 \left(\dfrac{r^2}{h^2}\right) } \\[4pt] &= \pi r \sqrt{h^2 + r^2}. \end{align*}\]
Par conséquent, la surface latérale du cône est de\(\pi r \sqrt{h^2 + r^2}\).
AnalyseLa surface d'un cône circulaire droit avec rayon\(r\) et hauteur\(h\) est généralement donnée sous la forme\(\pi r^2 + \pi r \sqrt{h^2 + r^2}\). La raison en est que la base circulaire fait partie du cône et que, par conséquent, la surface de la base\(\pi r^2\) est ajoutée à la surface latérale\(\pi r \sqrt{h^2 + r^2}\) que nous avons trouvée.
Déterminez la surface de la surface à l'aide du paramétrage\(\vecs r(u,v) = \langle u + v, \, u^2, \, 2v \rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 2\).
- Allusion
-
Utilisez l'équation \ ref {equation1}.
- Réponse
-
\(\≈ 43.02\)
Indique que la surface de la sphère\(x^2 + y^2 + z^2 = r^2\) est de\(4 \pi r^2\).
Solution
La sphère est paramétrée
\(r \, \cos \theta \, \sin \phi, \, r \, \sin \theta \, \sin \phi, \, r \, \cos \phi \rangle, \, 0 \leq \theta < 2\pi, \, 0 \leq \phi \leq \pi.\)
Les vecteurs tangents sont
\(\vecs t_{\theta} = \langle -r \, \sin \theta \, \sin \phi, \, r \, \cos \theta \, \sin \phi, \, 0 \rangle\)
et
\(\vecs t_{\phi} = \langle r \, \cos \theta \, \cos \phi, \, r \, \sin \theta \, \cos \phi, \, -r \, \sin \phi \rangle.\)
Par conséquent,
\[ \begin{align*}\vecs t_{\phi} \times \vecs t_{\theta} &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin^2 \theta \, \sin \phi \, \cos \phi + r^2 \cos^2 \theta \, \sin \phi \, \cos \phi \rangle \\[4pt] &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin \phi \, \cos \phi \rangle. \end{align*}\]
Maintenant,
\[ \begin{align*}||\vecs t_{\phi} \times \vecs t_{\theta} || &= \sqrt{r^4\sin^4\phi \, \cos^2 \theta + r^4 \sin^4 \phi \, \sin^2 \theta + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= \sqrt{r^4 \sin^4 \phi + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= r^2 \sqrt{\sin^2 \phi} \\[4pt] &= r \, \sin \phi.\end{align*}\]
Remarquez cela\(\sin \phi \geq 0\) sur le domaine des paramètres parce que\(0 \leq \phi < \pi\), et cela justifie l'équation\(\sqrt{\sin^2 \phi} = \sin \phi\). La surface de la sphère est
\[\int_0^{2\pi} \int_0^{\pi} r^2 \sin \phi \, d\phi \,d\theta = r^2 \int_0^{2\pi} 2 \, d\theta = 4\pi r^2. \nonumber \]
Nous avons dérivé la formule familière pour la surface d'une sphère à l'aide d'intégrales de surface.
Montrez que la surface du cylindre\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\) est de\(2\pi rh\). Notez que ce cylindre ne comprend pas les cercles supérieur et inférieur.
- Allusion
-
Utilisez le paramétrage standard d'un cylindre et suivez l'exemple précédent.
- Réponse
-
Avec le paramétrage standard d'un cylindre, l'équation \ ref {equation1} indique que la surface est de\(2 \pi rh\).
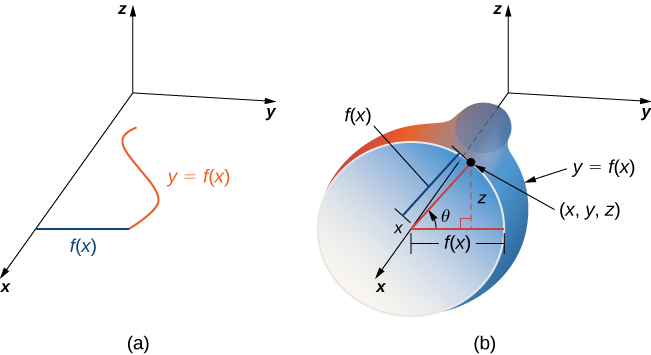
En plus de paramétrer des surfaces données par des équations ou des formes géométriques standard telles que des cônes et des sphères, nous pouvons également paramétrer des surfaces de révolution. Nous pouvons donc calculer la surface d'une surface de révolution en utilisant les mêmes techniques. \(y = f(x) \geq 0\)Soit une fonction à variable unique positive sur le domaine\(a \leq x \leq b\) et\(S\) soit la surface obtenue en tournant\(f\) autour de l'\(x\)axe (Figure\(\PageIndex{13}\)). \(\theta\)Soit l'angle de rotation. Ensuite,\(S\) peut être paramétré avec des paramètres\(x\) et\(\theta\) par
\[\vecs r(x, \theta) = \langle x, f(x) \, \cos \theta, \, f(x) \sin \theta \rangle, \, a \leq x \leq b, \, 0 \leq x \leq 2\pi. \nonumber \]
Détermine l'aire de la surface de révolution obtenue en tournant\(y = x^2, \, 0 \leq x \leq b\) autour de l'axe x (Figure\(\PageIndex{14}\)).
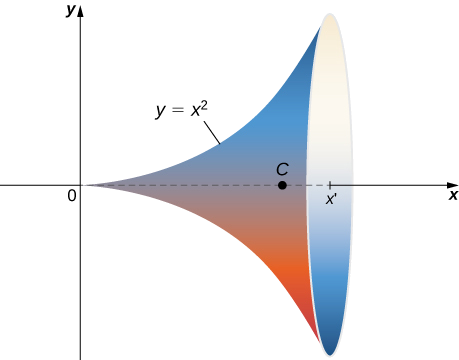
Solution
Cette surface est paramétrée\(\vecs r(x, \theta) = \langle x, \, x^2 \cos \theta, \, x^2 \sin \theta \rangle, \, 0 \leq x \leq b, \, 0 \leq x < 2\pi.\)
Les vecteurs tangents sont\( \vecs t_x = \langle 1, \, 2x \, \cos \theta, \, 2x \, \sin \theta \rangle\) et\(\vecs t_{\theta} = \langle 0, \, -x^2 \sin \theta, \, -x^2 \cos \theta \rangle\).
Par conséquent,
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \langle 2x^3 \cos^2 \theta + 2x^3 \sin^2 \theta, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \\[4pt] &= \langle 2x^3, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \end{align*}\]
et
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \sqrt{4x^6 + x^4\cos^2 \theta + x^4 \sin^2 \theta} \\[4pt] &= \sqrt{4x^6 + x^4} \\[4pt] &= x^2 \sqrt{4x^2 + 1} \end{align*}\]
L'aire de la surface de révolution est
\ [\ begin {align*} \ int_0^b \ int_0^ {2 \ pi} x^2 \ sqrt {4x^2 + 1} \, d \ theta \, dx &= 2 \ pi \ int_0^b x^2 \ sqrt {4x^2 + 1} \, dx \ \ [4 points]
&= 2 \ pi \ left [\ dfrac {1}} {64} \ left (2 \ sqrt {4x^2 + 1} (8x^3 + x) \, \ sinh^ {-1} (2x) \ right) \ right] _0^b \ \ [4pt]
&= 2 \ pi \ left [\ dfrac {1} {64} \ left (2) \ sqrt {4b^2 + 1} (8b^3 + b) \, \ sinh^ {-1} (2b) \ right) \ right]. \ end {align*} \]
Utilisez l'équation \ ref {equation1} pour trouver l'aire de la surface de révolution obtenue en faisant pivoter la courbe\(y = \sin x, \, 0 \leq x \leq \pi\) autour de l'\(x\)axe.
- Allusion
-
Utilisez le paramétrage des surfaces de révolution donné avant l'exemple\(\PageIndex{7}\).
- Réponse
-
\(2\pi (\sqrt{2} + \sinh^{-1} (1))\)
Intégrale de surface d'une fonction à valeur scalaire
Maintenant que nous pouvons paramétrer les surfaces et calculer leurs surfaces, nous sommes en mesure de définir des intégrales de surface. Examinons d'abord l'intégrale de surface d'une fonction à valeur scalaire. De manière informelle, l'intégrale de surface d'une fonction à valeur scalaire est analogue à une intégrale linéaire scalaire dans une dimension supérieure. Le domaine d'intégration d'une intégrale scalaire est une courbe paramétrée (un objet unidimensionnel) ; le domaine d'intégration d'une intégrale de surface scalaire est une surface paramétrée (un objet bidimensionnel). Par conséquent, la définition d'une intégrale de surface suit de très près la définition d'une intégrale linéaire. Pour les intégrales scalaires, nous avons découpé la courbe du domaine en petits morceaux, choisi un point dans chaque pièce, calculé la fonction à ce point et pris une limite de la somme de Riemann correspondante. Pour les intégrales de surface scalaire, nous découpons la région du domaine (qui n'est plus une courbe) en petits morceaux et procédons de la même manière.
\(S\)Soit une surface lisse par morceaux avec paramétrage\(\vecs{r}(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle \) avec un domaine de paramètres\(D\) et\(f(x,y,z)\) soit une fonction avec un domaine qui contient\(S\). Pour l'instant, supposons que le domaine des paramètres\(D\) est un rectangle, mais nous pouvons étendre la logique de base de la procédure à n'importe quel domaine de paramètres (le choix d'un rectangle consiste simplement à rendre la notation plus gérable). Divisez\(D\) le rectangle en\(D_{ij}\) sous-rectangles de largeur horizontale\(\Delta u\) et de longueur verticale\(\Delta v\). Supposons que\(i\)\(1\) la plage soit\(j\) comprise\(1\) entre\(m\) et et\(n\)\(D\) soit divisée en\(mn\) rectangles. Cette division\(D\) en sous-rectangles donne une division correspondante de\(S\) en morceaux\(S_{ij}\). Choisissez un point\(P_{ij}\) dans chaque pièce\(f\),\(S_{ij}\) évaluez\(P_{ij}\) à et multipliez par surface\(S_{ij}\) pour former la somme de Riemann.
\[\sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \, \Delta S_{ij}. \nonumber \]
Pour définir une intégrale de surface d'une fonction à valeur scalaire, nous laissons les aires des pièces\(S\) se réduire à zéro en prenant une limite.
L'intégrale de surface d'une fonction à valeur scalaire\(f\) sur une surface lisse par morceaux\(S\) est
\[\iint_S f(x,y,z) dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}. \nonumber \]
Encore une fois, remarquez les similitudes entre cette définition et la définition d'une intégrale linéaire scalaire. Lors de la définition d'une intégrale linéaire, nous découpons une courbe en morceaux, évaluons une fonction à un point de chaque pièce et laissons la longueur des pièces se réduire à zéro en prenant la limite de la somme de Riemann correspondante. Pour définir une intégrale de surface, nous découpons une surface en morceaux, évaluons une fonction à un point de chaque pièce et laissons la surface des pièces se réduire à zéro en prenant la limite de la somme de Riemann correspondante. Ainsi, une intégrale de surface est similaire à une intégrale linéaire mais dans une dimension supérieure.
La définition d'une intégrale linéaire scalaire peut être étendue à des domaines de paramètres qui ne sont pas des rectangles en utilisant la même logique que celle utilisée précédemment. L'idée de base est de découper le domaine des paramètres en petits morceaux, de choisir un point d'échantillonnage dans chaque pièce, etc. La forme exacte de chaque pièce dans le domaine de l'échantillon n'a plus aucune importance à mesure que les zones des pièces se réduisent à zéro.
Les intégrales de surface scalaires sont difficiles à calculer à partir de la définition, tout comme les intégrales de lignes scalaires le sont. Pour développer une méthode qui facilite le calcul des intégrales de surface, nous approximons les surfaces\(\Delta S_{ij}\) avec de petits morceaux d'un plan tangent, comme nous l'avons fait dans la sous-section précédente. Rappelez la définition des vecteurs\(\vecs t_u\) et\(\vecs t_v\) :
\[\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\, \text{and} \, \vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
D'après le matériel que nous avons déjà étudié, nous savons que
\[\Delta S_{ij} \approx ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})|| \,\Delta u \,\Delta v. \nonumber \]
Par conséquent,
\[\iint_S f(x,y,z) \,dS \approx \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij})|| \vecs t_u(P_{ij}) \times \vecs t_v(P_{ij}) ||\,\Delta u \,\Delta v. \nonumber \]
Cette approximation devient arbitrairement proche à\(\displaystyle \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}\) mesure que nous augmentons le nombre de pièces\(S_{ij}\) en lâchant\(m\) et en\(n\) allant à l'infini. Nous avons donc l'équation suivante pour calculer les intégrales de surface scalaires :
\[\iint_S f(x,y,z)\,dS = \iint_D f(\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA. \label{scalar surface integrals} \]
L'équation \ ref {intégrales de surface scalaires} nous permet de calculer une intégrale de surface en la transformant en une intégrale double. Cette équation pour les intégrales de surface est analogue à l'équation pour les intégrales linéaires :
\[\iint_C f(x,y,z)\,ds = \int_a^b f(\vecs r(t))||\vecs r'(t)||\,dt. \nonumber \]
Dans ce cas, le vecteur\(\vecs t_u \times \vecs t_v\) est perpendiculaire à la surface, tandis que le vecteur\(\vecs r'(t)\) est tangent à la courbe.
Calculer l'intégrale de
\[\iint_S 5 \, dS, \nonumber \]
où\(S\) est la surface avec paramétrage\(\vecs r(u,v) = \langle u, \, u^2, \, v \rangle\) pour\(0 \leq u \leq 2\) et\(0 \leq v \leq u\).
Solution
Notez que ce domaine de paramètres\(D\) est un triangle et qu'il n'est donc pas rectangulaire. Ce n'est cependant pas un problème, car l'équation \ ref {intégrales de surface scalaire} n'impose aucune restriction quant à la forme du domaine des paramètres.
Pour utiliser l'équation \ ref {intégrales de surface scalaire} pour calculer l'intégrale de surface, nous trouvons d'abord des vecteurs\(\vecs t_u\) et\(\vecs t_v\). Notez que\(\vecs t_u = \langle 1, 2u, 0 \rangle\) et\(\vecs t_v = \langle 0,0,1 \rangle\). Par conséquent,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \nonumber \\ 1 & 2u & 0 \nonumber \\ 0 & 0 & 1 \end{vmatrix} = \langle 2u, \, -1, \, 0 \rangle\ \nonumber \]
et
\[||\vecs t_u \times \vecs t_v|| = \sqrt{1 + 4u^2}. \nonumber \]
Par l'équation \ ref {intégrales de surface scalaire},
\ [\ begin {align*} \ IInt_S 5 \, dS &= 5 \ iInt_D \ sqrt {1 + 4u^2} \, dA \ \
&= 5 \ int_0^2 \ int_0^u \ sqrt {1 + 4u^2} \, dv \, du = 5 \ int_0^2 u \ sqrt {1 + 4u^2} \, du \ \
&= 5 \ left [\ dfrac {(1+4u^2) ^ {3/2}} {3} \ right] _0^2 \ \
&= \ dfrac {5 (17^ {3/2} -1)} {3} \ environ 115. 15. \ end {align*} \]
Calculez l'intégrale de surface\[\iint_S (x + y^2) \, dS, \nonumber \] où\(S\) se trouve le cylindre\(x^2 + y^2 = 4, \, 0 \leq z \leq 3\) (Figure\(\PageIndex{15}\)).
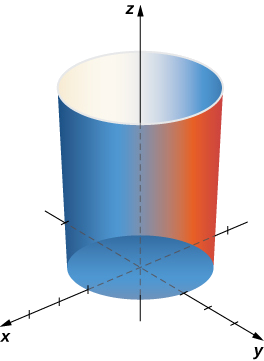
Solution
Pour calculer l'intégrale de surface, il faut d'abord paramétrer le cylindre. Un paramétrage est\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, 0 \leq u \leq 2\pi, \, 0 \leq v \leq 3.\)
Les vecteurs tangents sont\(\vecs t_u = \langle \sin u, \, \cos u, \, 0 \rangle\) et\(\vecs t_v = \langle 0,0,1 \rangle\). Ensuite,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \end{vmatrix} = \langle \cos u, \, \sin u, \, 0 \rangle \nonumber \]
et\(||\vecs t_u \times \vecs t_v || = \sqrt{\cos^2 u + \sin^2 u} = 1\). Par l'équation \ ref {intégrales de surface scalaire},
\ [\ begin {align*} \ IInt_s f (x, y, z) dS &= \ iInt_D f (\ vecs r (u, v)) || \ vecs t_u \ times \ vecs t_v|| \, dA \ \
&= \ int_0^3 \ int_0^ {2 \ pi} (\ cos u + \ sin^2 u) \, du \ d, v \ \
&= \ int_0^3 \ left [\ sin u + \ dfrac {u} {2} - \ dfrac {\ sin (2u)} {4} \ right] _0^ {2 \ pi} \, dv \ \
&= \ int_0^3 \ pi \, dv = 3 \ pi. \ end {align*} \]
Calculer\[\iint_S (x^2 - z) \,dS, \nonumber \] où\(S\) se trouve la surface avec paramétrage\(\vecs r(u,v) = \langle v, \, u^2 + v^2, \, 1 \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3.\)
- Allusion
-
Utilisez l'équation \ ref {intégrales de surface scalaire}.
- Réponse
-
24
Calculez l'intégrale de surface\[\iint_S f(x,y,z)\,dS, \nonumber \] où\(f(x,y,z) = z^2\) et\(S\) est la surface constituée du morceau de sphère\(x^2 + y^2 + z^2 = 4\) situé sur ou au-dessus du plan\(z = 1\) et du disque qui est entouré par le plan d'intersection\(z = 1\) et la sphère donnée (Figure\(\PageIndex{16}\)).
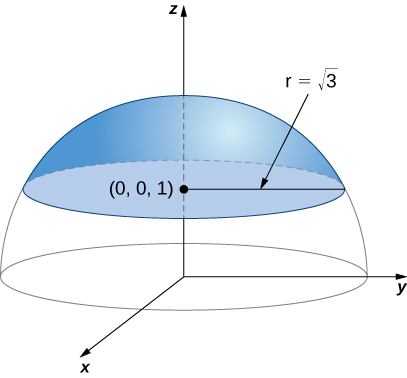
Solution
Remarquez que ce n'\(S\)est pas lisse mais qu'il est lisse par morceaux ; cela\(S\) peut être écrit comme l'union de sa base\(S_1\) et de son sommet sphérique\(S_2\), et les deux\(S_1\) et\(S_2\) sont lisses. Par conséquent, pour calculer
\[\iint_S z^2 dS, \nonumber \]
nous écrivons cette intégrale comme
\[\iint_{S_1} z^2 \,dS + \iint_{S_2} z^2 \,dS \nonumber \]
et nous calculons des intégrales
\[\iint_{S_1} z^2 \,dS \nonumber \]
et
\[\iint_{S_2}Z^2 \,dS. \nonumber \]
Tout d'abord, nous calculons\(\displaystyle \iint_{S_1} z^2 \,dS.\) Pour calculer cette intégrale, nous avons besoin d'un paramétrage de\(S_1\). Cette surface est un disque dans un plan\(z = 1\) centré sur\((0,0,1)\). Pour paramétrer ce disque, il faut connaître son rayon. Puisque le disque est formé là où le plan\(z = 1\) croise la sphère\(x^2 + y^2 + z^2 = 4\), nous pouvons le remplacer par\(z = 1\) une équation\(x^2 + y^2 + z^2 = 4\) :
\[x^2 + y^2 + 1 = 4 \Rightarrow x^2 + y^2 = 3. \nonumber \]
Par conséquent, le rayon du disque est\(\sqrt{3}\) et un paramétrage de\(S_1\) est\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq \sqrt{3}, \, 0 \leq v \leq 2\pi\). Les vecteurs tangents sont\(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) et\(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, \, 0 \rangle\), donc
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \cos v & \sin v & 0 \\ -u\sin v & u\cos v& 0 \end{vmatrix} = \langle 0, \, 0, u \, \cos^2 v + u \, \sin^2 v \rangle = \langle 0, 0, u \rangle. \nonumber \]
L'amplitude de ce vecteur est\(u\). Par conséquent,
\ [\ begin {align*} \ iint_ {S_1} z^2 \, dS &= \ int_0^ {\ sqrt {3}} \ int_0^ {2 \ pi} f (r (u, v)) ||t_u \ times t_v|| \, dv \, du \ \
&= \ int_0^ {\ sqrt {3}} \ int_0^ {\ sqrt {3}} \ int_0^ 2 \ pi} u \, dv \, du \ \
&= 2 \ pi \ int_0^ {\ sqrt {3}} u \, du \ \
&= 2 \ pi \ sqrt {3}. \ end {align*} \]
Maintenant, nous calculons
\[\iint_{S_2} \,dS. \nonumber \]
Pour calculer cette intégrale, nous avons besoin d'un paramétrage de\(S_2\). Le paramétrage de la sphère complète\(x^2 + y^2 + z^2 = 4\) est
\[\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. \nonumber \]
Comme nous ne prenons que la partie de la sphère sur ou au-dessus du plan\(z = 1\), nous devons restreindre le domaine de\(\phi\). Pour voir la distance parcourue par cet angle, notez que l'angle peut être situé dans un triangle droit, comme le montre la figure\(\PageIndex{17}\) (cela\(\sqrt{3}\) vient du fait que la base de\(S\) est un disque avec un rayon\(\sqrt{3}\)). Par conséquent, la tangente de\(\phi\) est\(\sqrt{3}\), ce qui implique que\(\phi\) c'est\(\pi / 6\). Nous avons maintenant un paramétrage de\(S_2\) :
\(\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi / 3.\)
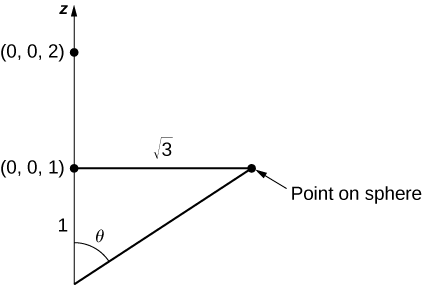
Les vecteurs tangents sont\(\vecs t_{\phi} = \langle 2 \, \cos \theta \, \cos \phi, \, 2 \, \sin \theta \,\cos \phi, \, -2 \, \sin \phi \rangle\) et\(\vecs t_{\theta} = \langle - 2 \sin \theta \sin \phi, \, u\cos \theta \sin \phi, \, 0 \rangle\), donc
\ [\ begin {align*} \ vecs t_ {\ phi} \ times \ vecs t_ {\ theta} &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ nonumber \ \ 2 \ cos \ theta \ cos \ phi & 2 \ cos \ theta \ cos \ phi & -2 \ sin \ phi \ \ -2 \ sin \ thêta \ sin \ phi et 2 \ cos \ thêta \ sin \ phi et 0 \ end {vmatrix} \ \ [4 points]
&= \ langle 4 \, \ cos \ thêta \, \ sin^2 \ phi, \, 4 \, \ sin \ thêta \, \ sin^2 \ phi, \, 4 \, \ cos^2 \ thêta \, \ cos \ phi \, \ sin \ phi + 4 \, \ sin^2 \ thêta \, \ cos \ phi \ phi \ rangle \ \ [4 pt]
&= \ langle 4 \, \ cos \ thêta \, \ sin^2 \ phi, \, 4 \, \ sin \ thêta \, \ sin^2 \ phi, \, 4 \, \ cos \ phi \, \ sin \ phi \ rangle. \ end {align*} \]
L'amplitude de ce vecteur est
\ [\ begin {align*} \ vecs t_ {\ phi} \ times \ vecs t_ {\ theta} &= \ sqrt {16 \, \ cos^2 \ thêta \, \ sin^4 \ phi + 16 \, \ sin^2 \ thêta \, \ sin^4 \ phi + 16 \, \ cos^2 \ phi \, \ sin^2 \ phi} \ [4 pt]
&= 4 \ sqrt {\ sin^4 \ phi + \ cos^2 \ phi \, \ sin^2 \ phi}. \ end {align*} \]
Par conséquent,
\ [\ begin {align*} \ iint_ {S_2} z \, dS &= \ int_0^ {\ pi/6} \ int_0^ {2 \ pi} f (\ vecs r (\ phi, \ thêta)) || \ vecs t_ {\ phi} \ times \ vecs t_ {\ thêta} || \, d \ thêta \, d \ phi \
&= \ int_0^ {\ pi/6} \ int_0^ {2 \ pi} 16 \, \ cos^2 \ phi \ sqrt {\ sin^4 \ phi + \ cos^2 \ phi \, \ sin^2 \ phi} \, d \ thêta \, d \ phi \ \
&= 32 \ pi \ int_0^ {\ pi/6} \ cos^2 \ phi \ sqrt {\ sin^4 \ phi + \ cos^2 \ phi \, \ sin^2 \ phi} \, d \ phi \ \
&= 32 \ pi \ int_0^ {\ pi/6} \ cos^2 \ phi \, \ sin \ phi \ sqrt {\ sin^2 \ phi \ cos^2 \ phi} \, d \ phi \ \
&= 32 \ pi \ int_0^ {\ pi/6} \ cos^2 \ phi \, \ sin \ phi \, d \ phi \ \
& = 32 \ pi \ left [- \ dfrac {\ cos^3 \ phi} {3} \ droite] _0^ {\ pi/6} \ \
&= 32 \ pi \ left [\ dfrac {1} {3} - \ dfrac {\ sqrt {3}}} {8} \ right] = \ dfrac {32 \ pi} {3} - 4 \ sqrt {3}. \ end {align*} \]
Depuis
\[\iint_S z^2 \,dS = \iint_{S_1}z^2 \,dS + \iint_{S_2}z^2 \,dS, \nonumber \]
nous avons
\[\iint_S z^2 \,dS = (2\pi - 4) \sqrt{3} + \dfrac{32\pi}{3}. \nonumber \]
Analyse
Dans cet exemple, nous avons divisé une intégrale de surface sur une surface par morceaux en ajoutant des intégrales de surface sur des sous-surfaces lisses. Il n'y avait que deux sous-surfaces lisses dans cet exemple, mais cette technique s'étend à un nombre limité de sous-surfaces lisses.
Calculez l'intégrale de la ligne\(\displaystyle \iint_S (x - y) \, dS,\) où\(S\) se trouve le cylindre\(x^2 + y^2 = 1, \, 0 \leq z \leq 2\), y compris le haut et le bas circulaires
- Allusion
-
Divisez l'intégrale en trois intégrales de surface distinctes.
- Réponse
-
0
Les intégrales de surface scalaire ont plusieurs applications dans le monde réel. Rappelons que les intégrales de lignes scalaires peuvent être utilisées pour calculer la masse d'un fil en fonction de sa fonction de densité. De la même manière, nous pouvons utiliser des intégrales de surface scalaires pour calculer la masse d'une feuille en fonction de sa fonction de densité. Si une fine feuille de métal a la forme de la surface\(S\) et que la densité de la feuille au point\((x,y,z)\) est égale\(\rho(x,y,z)\), alors la masse\(m\) de la feuille est
\[\displaystyle m = \iint_S \rho (x,y,z) \,dS. \label{mass} \]
Une feuille de métal plate a la forme d'une surface\(z = 1 + x + 2y\) située au-dessus du rectangle\(0 \leq x \leq 4\) et\(0 \leq y \leq 2\). Si la densité de la feuille est donnée par\(\rho (x,y,z) = x^2 yz\), quelle est la masse de la feuille ?
Solution
\(S\)Soit la surface qui décrit la feuille. Ensuite, la masse de la feuille est donnée par\(\displaystyle m = \iint_S x^2 yx \, dS.\) Pour calculer cette intégrale de surface, nous avons d'abord besoin d'un paramétrage de\(S\). Puisque\(S\) est donné par la fonction\(f(x,y) = 1 + x + 2y\), un paramétrage de\(S\) est\(\vecs r(x,y) = \langle x, \, y, \, 1 + x + 2y \rangle, \, 0 \leq x \leq 4, \, 0 \leq y \leq 2\).
Les vecteurs tangents sont\(\vecs t_x = \langle 1,0,1 \rangle\) et\(\vecs t_y = \langle 1,0,2 \rangle\). Par conséquent,\(\vecs t_x + \vecs t_y = \langle -1,-2,1 \rangle\) et\(||\vecs t_x \times \vecs t_y|| = \sqrt{6}\).
Selon la définition de l'intégrale de la ligne (Section 16.2), \ [\ begin {align*} m &= \ iInt_S x^2 yz \, dS \ \ [4pt]
&= \ sqrt {6} \ int_0^4 \ int_0^2 x^2 y (1 + x + 2y) \, dy \, dx \ \ [4pt]
&= \ sqrt {6} \ int_0^4 \ dfrac {22x^2} {3} + 2x^3 \, dx \ \ [4 points]
&= \ dfrac {2560 \ sqrt { 6}} {9} \ environ 696,74. \ end {align*} \]
Une pièce de métal a une forme modélisée par un paraboloïde\(z = x^2 + y^2, \, 0 \leq z \leq 4,\) et la densité du métal est donnée par\(\rho (x,y,z) = z + 1\). Déterminez la masse de la pièce de métal.
- Allusion
-
La masse d'une feuille est donnée par l'équation \ ref {mass}. Un paramétrage utile d'un paraboloïde a été donné dans un exemple précédent.
- Réponse
-
\(38.401 \pi \approx 120.640\)
Orientation d'une surface
Rappelons que lorsque nous avons défini une intégrale scalaire, nous n'avions pas à nous soucier de l'orientation de la courbe d'intégration. Il en était de même pour les intégrales de surface scalaires : nous n'avions pas à nous soucier d'une « orientation » de la surface d'intégration.
D'un autre côté, lorsque nous avons défini des intégrales de lignes vectorielles, la courbe d'intégration avait besoin d'une orientation. C'est-à-dire que nous avions besoin de la notion de courbe orientée pour définir une intégrale vectorielle sans ambiguïté. De même, lorsque nous définissons une intégrale de surface d'un champ vectoriel, nous avons besoin de la notion de surface orientée. Une surface orientée reçoit une orientation « vers le haut » ou « vers le bas » ou, dans le cas de surfaces telles qu'une sphère ou un cylindre, une orientation « vers l'extérieur » ou « vers l'intérieur ».
Soit S une surface lisse. À tout moment\((x,y,z)\)\(S\), nous pouvons identifier deux vecteurs normaux unitaires\(\vecs N\) et\(-\vecs N\). S'il est possible de choisir un vecteur normal unitaire\(\vecs N\) à chaque point de\(S\) manière\((x,y,z)\) à ce qu'il\(\vecs N\) varie continuellement\(S\), alors\(S\) il est « orientable ». Un tel choix de vecteur normal unitaire en chaque point donne l'orientation d'une surface\(S\). Si vous considérez que le champ normal décrit le débit d'eau, alors le côté de la surface vers lequel l'eau s'écoule est le côté « négatif » et le côté de la surface par lequel l'eau s'écoule est le côté « positif ». De manière informelle, un choix d'orientation donne\(S\) un côté « extérieur » et un côté « intérieur » (ou un côté « vers le haut » et un côté « vers le bas »), tout comme le choix de l'orientation d'une courbe donne à la courbe des directions « vers l'avant » et « vers l'arrière ».
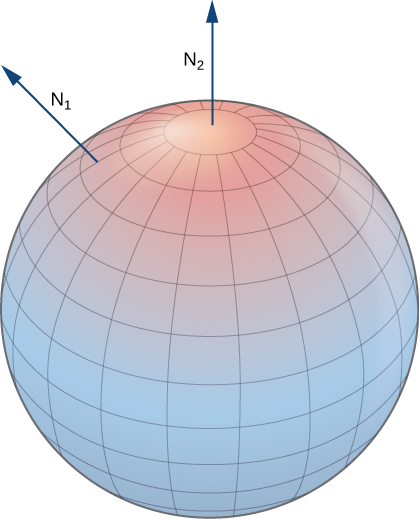
Les surfaces fermées telles que les sphères sont orientables : si nous choisissons le vecteur normal vers l'extérieur en chaque point de la surface de la sphère, les vecteurs normaux unitaires varient de façon continue. C'est ce que l'on appelle l'orientation positive de la surface fermée (Figure\(\PageIndex{18}\)). Nous pouvons également choisir le vecteur normal vers l'intérieur à chaque point pour donner une orientation « vers l'intérieur », qui est l'orientation négative de la surface.
Une partie du graphe de toute fonction lisse\(z = f(x,y)\) est également orientable. Si nous choisissons le vecteur normal unitaire qui pointe « au-dessus » de la surface à chaque point, les vecteurs normaux unitaires varient de façon continue sur la surface. Nous pouvons également choisir le vecteur normal unitaire qui pointe « sous » la surface à chaque point. Pour obtenir une telle orientation, nous paramétrons le graphe de de la\(f\) manière standard :\(\vecs r(x,y) = \langle x,\, y, \, f(x,y)\rangle\), où\(x\) et\(y\) varions sur le domaine de\(f\). Alors,\(\vecs t_x = \langle 1,0,f_x \rangle\) et donc\(\vecs t_y = \langle 0,1,f_y \rangle \), le produit croisé\(\vecs t_x \times \vecs t_y\) (qui est normal à la surface en tout point de la surface) est\(\langle -f_x, \, -f_y, \, 1 \rangle \) Puisque la\(z\) composante -de ce vecteur est un, le vecteur normal unitaire correspondant pointe « vers le haut », et le côté ascendant de la surface est choisi pour soyez le côté « positif ».
\(S\)Soit une surface lisse orientable avec paramétrage\(\vecs r(u,v)\). Pour chaque point de\(\vecs r(a,b)\) la surface, les vecteurs A\(\vecs t_u\) et\(\vecs t_v\) se situent dans le plan tangent à ce point. \(\vecs t_u \times \vecs t_v\)Le vecteur est normal au plan tangent à ce point\(\vecs r(a,b)\) et est donc normal\(S\) à ce point. Par conséquent, le choix du vecteur normal unitaire
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
donne l'orientation de la surface\(S\).
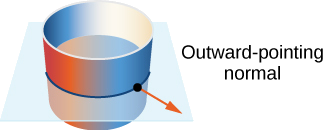
Donnez l'orientation du cylindre\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\).
Solution
Cette surface est paramétrée\(\vecs r(u,v) = \langle r \, \cos u, \, r \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h.\)
Les vecteurs tangents sont\(\vecs t_u = \langle -r \, \sin u, \, r \, \cos u, \, 0 \rangle \) et\(\vecs t_v = \langle 0,0,1 \rangle\). Pour obtenir une orientation de la surface, nous calculons le vecteur normal unitaire
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
Dans ce cas,\(\vecs t_u \times \vecs t_v = \langle r \, \cos u, \, r \, \sin u, \, 0 \rangle\) et donc
\[||\vecs t_u \times \vecs t_v|| = \sqrt{r^2 \cos^2 u + r^2 \sin^2 u} = r. \nonumber \]
L'orientation du cylindre est
\[\vecs N(u,v) = \dfrac{\langle r \, \cos u, \, r \, \sin u, \, 0 \rangle }{r} = \langle \cos u, \, \sin u, \, 0 \rangle. \nonumber \]
Notez que tous les vecteurs sont parallèles au\(xy\) plan, ce qui devrait être le cas pour les vecteurs normaux au cylindre. De plus, tous les vecteurs pointent vers l'extérieur, et il s'agit donc d'une orientation du cylindre vers l'extérieur (Figure\(\PageIndex{19}\)).
Donnez l'orientation « vers le haut » du graphique de\(f(x,y) = xy\).
- Allusion
-
Paramétrez la surface et utilisez le fait que la surface est le graphe d'une fonction.
- Réponse
-
\[\vecs{N}(x,y) = \left\langle \dfrac{-y}{\sqrt{1+x^2+y^2}}, \, \dfrac{-x}{\sqrt{1+x^2+y^2}}, \, \dfrac{1}{\sqrt{1+x^2+y^2}} \right\rangle \nonumber \]
Comme chaque courbe a une direction « vers l'avant » et « vers l'arrière » (ou, dans le cas d'une courbe fermée, une direction dans le sens des aiguilles d'une montre et dans le sens antihoraire), il est possible de donner une orientation à n'importe quelle courbe. Il est donc possible de considérer chaque courbe comme une courbe orientée. Ce n'est toutefois pas le cas pour les surfaces. Certaines surfaces ne peuvent pas être orientées ; ces surfaces sont dites non orientables. Essentiellement, une surface peut être orientée si elle possède un côté « intérieur » et un côté « extérieur », ou un côté « vers le haut » et un côté « vers le bas ». Certaines surfaces sont tordues de telle sorte qu'il n'existe aucune notion bien définie de côté « intérieur » ou « extérieur ».
L'exemple classique de surface non orientable est la bande de Möbius. Pour créer une bande de Möbius, prenez une bande de papier rectangulaire, tournez à moitié la feuille de papier et collez les extrémités ensemble (Figure\(\PageIndex{20}\)). En raison de la demi-torsion de la bande, la surface ne présente ni côté « extérieur » ni côté « intérieur ». Si vous imaginez que vous placez un vecteur normal à un point de la bande et que le vecteur se déplace tout autour de la bande, alors (à cause de la demi-torsion) le vecteur pointe dans la direction opposée lorsqu'il revient à sa position d'origine. Par conséquent, la bande n'a vraiment qu'un seul côté.

Comme certaines surfaces ne sont pas orientables, il n'est pas possible de définir une intégrale de surface vectorielle sur toutes les surfaces lisses par morceaux. Cela contraste avec les intégrales de lignes vectorielles, qui peuvent être définies sur n'importe quelle courbe lisse par morceaux.
Intégrale de surface d'un champ vectoriel
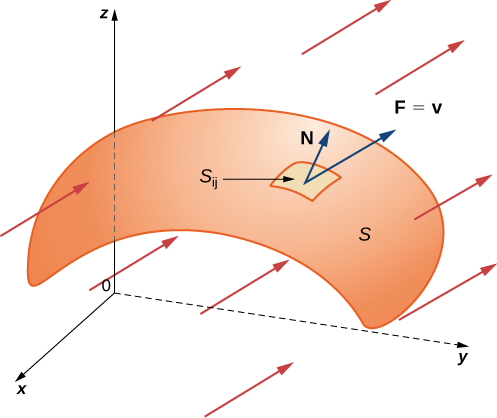
Avec l'idée de surfaces orientables en place, nous sommes maintenant prêts à définir une intégrale de surface d'un champ vectoriel. La définition est analogue à la définition du flux d'un champ vectoriel le long d'une courbe plane. Rappelez-vous que s'il s'\(\vecs{F}\)agit d'un champ vectoriel bidimensionnel et\(C\) d'une courbe plane, alors la définition du flux de\(\vecs{F}\) long\(C\) impliquait de découper\(C\) en petits morceaux, de choisir un point à l'intérieur de chaque pièce et de calculer\(\vecs{F} \cdot \vecs{N}\) au point (où se\(\vecs{N}\) trouve le unité (vecteur normal au point). La définition d'une intégrale de surface d'un champ vectoriel procède de la même manière, sauf que maintenant nous découpons la surface\(S\) en petits morceaux, choisissons un point dans la petite pièce (bidimensionnelle) et calculons\(\vecs{F} \cdot \vecs{N}\) au point.
Pour placer cette définition dans un environnement réel, supposons\(S\) une surface orientée avec un vecteur normal unitaire\(\vecs{N}\). \(\vecs{v}\)Soit le champ de vitesse d'un fluide qui s'écoule\(S\), et supposons que le fluide ait une densité\(\rho(x,y,z)\) Imaginez que le fluide circule à travers\(S\), mais qu'il\(S\) soit complètement perméable afin de ne pas gêner l'écoulement du fluide (Figure\(\PageIndex{21}\)). Le flux massique du fluide est le débit massique par unité de surface. Le flux massique est mesuré en masse par unité de temps et par unité de surface. Comment pourrions-nous calculer le flux massique du fluide à travers\(S\) ?
Le débit, mesuré en masse par unité de temps et par unité de surface, est de\(\rho \vecs N\). Pour calculer le flux massique à travers\(S\),\(S\) coupez-le en petits morceaux\(S_{ij}\). Si elle\(S_{ij}\) est suffisamment petite, elle peut être approximée par un plan tangent à un point\(P\) donné\(S_{ij}\). Par conséquent, le vecteur normal unitaire at\(P\) peut être utilisé pour obtenir une approximation\(\vecs N(x,y,z)\) sur l'ensemble de la pièce,\(S_{ij}\) car le vecteur normal d'un plan ne change pas lorsque nous nous déplaçons dans le plan. La composante du vecteur\(\rho v\) en P dans la direction de\(\vecs{N}\) est\(\rho \vecs v \cdot \vecs N\) à\(P\). Comme\(S_{ij}\) il est petit, le produit scalaire\(\rho v \cdot N\) change très peu à mesure que nous varions d'une région à l'autre\(S_{ij}\) et\(\rho \vecs v \cdot \vecs N\) peut donc être considéré comme approximativement constant à travers\(S_{ij}\). Pour approximer la masse de fluide par unité de temps s'écoulant\(S_{ij}\) (et pas seulement localement au point\(P\)), nous devons multiplier\((\rho \vecs v \cdot \vecs N) (P)\) par la surface de\(S_{ij}\). Par conséquent, la masse de fluide par unité de temps s'écoulant\(S_{ij}\) dans la direction de\(\vecs{N}\) peut être approximée par l'\((\rho \vecs v \cdot \vecs N)\Delta S_{ij}\)endroit\(\vecs{N}\)\(\rho\) et\(\vecs{v}\) est toutes évaluées à\(P\) (Figure\(\PageIndex{22}\)). Ceci est analogue au flux d'un champ vectoriel bidimensionnel à\(\vecs{F}\) travers une courbe plane\(C\), dans lequel nous avons approximé le flux sur un petit morceau de\(C\) avec l'expression\((\vecs{F} \cdot \vecs{N}) \,\Delta s\). Pour approximer le flux massique à travers\(S\), formez la somme
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
À mesure que les pièces\(S_{ij}\) deviennent plus petites, la somme
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij} \nonumber \]
se rapproche arbitrairement du flux de masse. Par conséquent, le flux massique est
\[\iint_s \rho \vecs v \cdot \vecs N \, dS = \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Il s'agit de l'intégrale de surface d'un champ vectoriel. Le fait de laisser le champ vectoriel\(\rho \vecs{v}\) être un champ vectoriel arbitraire\(\vecs{F}\) conduit à la définition suivante.
\(\vecs{F}\)Soit un champ vectoriel continu avec un domaine qui contient une surface orientée\(S\) avec un vecteur normal unitaire\(\vecs{N}\). L'intégrale de surface de\(\vecs{F}\) over\(S\) est
\[\iint_S \vecs{F} \cdot \vecs{S} = \iint_S \vecs{F} \cdot \vecs{N} \,dS. \label{surfaceI} \]
Remarquez le parallèle entre cette définition et la définition de l'intégrale d'une ligne vectorielle\(\displaystyle \int_C \vecs F \cdot \vecs N\, dS\). Une intégrale de surface d'un champ vectoriel est définie de la même manière qu'une intégrale de ligne de flux à travers une courbe, sauf que le domaine d'intégration est une surface (un objet bidimensionnel) plutôt qu'une courbe (un objet unidimensionnel). L'intégrale\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) est appelée le flux transversal\(S\),\(\vecs{F}\) tout comme l'intégrale\(\displaystyle \int_C \vecs F \cdot \vecs N\,dS\) est le flux de la courbe\(\vecs F\) transversale\(C\). Une intégrale de surface sur un champ vectoriel est également appelée intégrale de flux.
Tout comme pour les intégrales de lignes vectorielles, l'intégrale de surface\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) est plus facile à calculer une\(S\) fois la surface paramétrée. \(\vecs r(u,v)\)Soit un paramétrage de\(S\) avec un domaine de paramètres\(D\). Ensuite, le vecteur normal unitaire est donné par\(\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||}\) et, à partir de l'équation \ ref {SurfaceI}, nous avons
\ [\ begin {align*} \ Int_C \ vecs F \ cdot \ vecs N \, dS &= \ iInt_S \ vecs F \ cdot \ dfrac {\ vecs t_u \ times \ vecs t_v} {|| \ vecs t_u \ times \ vecs t_v||} \, dS \ \ [4pt]
&= \ iInt_D \ left (\ vecs t_v|| s F (\ vecs r (u, v)) \ cdot \ drac {\ vecs t_u \ times \ vecs t_v} {|| \ vecs t_u \ times \ vecs t_v||} \ right) || \ vecs t_u \ times \ vecs t_v || \, dA \ \ [4pt]
&= \ iInt_D (\ vecs F (\ vecs r (u, v)) \ cdot (\ vecs t_u \ times \ vecs t_v)) \, dA. \ end {align*} \]
Par conséquent, pour calculer une intégrale de surface sur un champ vectoriel, nous pouvons utiliser l'équation
\[\iint_S \vecs F \cdot \vecs N\, dS = \iint_D (\vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v)) \,dA. \label{equation 5} \]
Calculer l'intégrale de surface
\[\iint_S \vecs F \cdot \vecs N\,dS, \nonumber \]
où\(\vecs{F} = \langle -y,x,0\rangle\) et\(S\) est la surface avec paramétrage
\[\vecs r(u,v) = \langle u,v^2 - u, \, u + v\rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 4. \nonumber \]
Solution
Les vecteurs tangents sont\(\vecs t_u = \langle 1,-1,1\rangle\) et\(\vecs t_v = \langle 0,2v,1\rangle\). Par conséquent,
\[\vecs t_u \times \vecs t_v = \langle -1 -2v, -1, 2v\rangle. \nonumber \]
Par équation \ ref {équation 5},
\[ \begin{align*} \iint_S \vecs F \cdot dS &= \int_0^4 \int_0^3 F (\vecs r(u,v)) \cdot (\vecs t_u \times \vecs t_v) \, du \,dv \\[4pt] &= \int_0^4 \int_0^3 \langle u - v^2, \, u, \, 0\rangle \cdot \langle -1 -2v, \, -1, \, 2v\rangle \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 [(u - v^2)(-1-2v) - u] \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 (2v^3 + v^2 - 2uv - 2u) \, du\,dv \\[4pt] &= \int_0^4 \left.[2v^3u + v^2u - vu^2 - u^2]\right|_0^3 \, dv \\[4pt] &= \int_0^4 (6v^3 + 3v^2 - 9v - 9) \, dv \\[4pt] &= \left[ \dfrac{3v^4}{2} + v^3 - \dfrac{9v^2}{2} - 9v\right]_0^4\\[4pt] &= 340. \end{align*}\]
Par conséquent, le flux de\(\vecs{F}\) croix\(S\) est de 340.
Calculez l'intégrale de surface\[\iint_S \vecs F \cdot \vecs N \, dS, \nonumber \] où\(\vecs F = \langle 0, -z, y \rangle\) et\(S\) est la partie de la sphère unitaire dans le premier octant orientée vers l'extérieur.
- Allusion
-
Utilisez l'équation \ ref {équation 5}.
- Réponse
-
0
\(\vecs v(x,y,z) = \langle 2x, \, 2y, \, z\rangle\)Représentent un champ de vitesse (en unités de mètres par seconde) d'un fluide de densité constante de 80 kg/m 3. \(S\)Soit un hémisphère\(x^2 + y^2 + z^2 = 9\) avec un\(z \leq 0\) tel qui\(S\) est orienté vers l'extérieur. Déterminez le débit massique du fluide traversant\(S\).
Solution
Un paramétrage de la surface est
\[\vecs r(\phi, \theta) = \langle 3 \, \cos \theta \, \sin \phi, \, 3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi/2. \nonumber \]
Comme dans l'exemple, les vecteurs tangents sont\(\vecs t_{\theta} = \langle -3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \theta \, \sin \phi, \, 0 \rangle \)\( \vecs t_{\phi} = \langle 3 \, \cos \theta \, \cos \phi, \, 3 \, \sin \theta \, \cos \phi, \, -3 \, \sin \phi \rangle,\) et leur produit croisé est
\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle. \nonumber \]
Notez que chaque composante du produit croisé est positive et que, par conséquent, ce vecteur donne l'orientation vers l'extérieur. Par conséquent, nous utilisons l'orientation
\(\vecs N = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle \)
pour la sphère.
Par \ label {SurfaceI},
\ [\ begin {align*} \ iInt_S \ rho v \ cdot \, dS &= 80 \ int_0^ {2 \ pi} \ int_0^ {\ pi/2} v (r (\ phi, \ thêta)) \ cdot (t_ {\ phi} \ times t_ {\ theta}) \, d \ phi \, d \ thêta \ \
&= 80 \ int_0^ {2 \ pi} \ int_0^ {\ pi/2} \ angle 6 \, \ cos \ thêta \, \ sin \ phi, \, 6 \, \ sin \ thêta \, \ sin \ phi, \, 3 \, \ cos \ phi \ rangle \ cdot \ langle 9 \, \ cos \ thêta \, \ sin^2 \ phi, \, 9 \, \ sin \ thêta \, \ sin^2 \ phi, \ 9 \, \ sin \ phi \, \ cos \ phi \ rangle \, d \ phi \, d \ thêta \ \
&= 80 \ int_0^ {2 \ pi} \ int_0^ {\ pi} \ int_0^ {\ pi/2} 54 \, \ sin^3 \ phi + 27 \, \ cos^2 \ phi \, \ sin \ phi \, d \ phi \, d \ thêta \ \
&= 80 \ int_0^ {2 \ pi} \ int_0^ {\ pi/2} 54 (1 - \ cos^2 \ phi) \, \ sin \ phi + 27 \ cos^2 \ phi \, \ sin \ phi \, d \ phi \, d \ thêta \ \
&= 80 \ int_0^ {2 \ pi} \ int_0^ {\ pi/2} 54 \, \ sin \ phi - 27 \, \ cos^2 \ phi \, \ sin \ phi \, d \ phi \, d \ thêta \ \
&= 80 \ int_0^ {2 \ pi} \ Big [-54 \, \ cos \ phi + 9 \, \ cos^3 \ phi \ Big] _ {\ phi =0} ^ {\ phi=2 \ pi} \, d \ thêta \ \
&=80 \ int_0^ {2 \ pi} 45 \, d \ thêta \ \
&= 7200 \ pi. \ end {align*} \ nonumber \]
Par conséquent, le débit massique est de\(7200\pi \, \text{kg/sec/m}^2\).
Soit\(\vecs v(x,y,z) = \langle x^2 + y^2, \, z, \, 4y \rangle\) m/sec un champ de vitesse d'un fluide de densité constante de 100 kg/m 3. \(S\)Soit le demi-cylindre\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) orienté vers l'extérieur. Calculez le flux massique du fluide à travers\(S\).
- Allusion
-
Utilisez \ label {SurfaceI}.
- Réponse
-
400 kg/sec/m
Dans l'exemple\(\PageIndex{14}\), nous avons calculé le flux massique, qui est le débit massique par unité de surface. Si nous voulons plutôt trouver le débit (mesuré en volume par temps), nous pouvons utiliser l'intégrale du flux
\[\iint_S \vecs v \cdot \vecs N \, dS, \nonumber \]
ce qui ne tient pas compte de la densité. Le débit d'un fluide étant mesuré en volume par unité de temps, le débit ne prend pas en compte la masse. Nous avons donc la caractérisation suivante du débit d'un fluide avec sa vitesse\(\vecs v\) sur une surface\(S\) :
\[\text{Flow rate of fluid across S} = \iint_S \vecs v \cdot dS. \nonumber \]
Pour calculer le débit du fluide dans l'exemple, il suffit de supprimer la constante de densité, qui donne un débit de\(90 \pi \, m^3/sec\).
Le flux massique et le débit sont tous deux importants en physique et en ingénierie. Le flux massique mesure la quantité de masse qui s'écoule sur une surface ; le débit mesure le volume de fluide qui s'écoule sur une surface.
En plus de modéliser le flux de fluide, les intégrales de surface peuvent être utilisées pour modéliser le flux de chaleur. Supposons que la température d'un point\((x,y,z)\) dans un objet soit\(T(x,y,z)\). Le flux de chaleur est alors un champ vectoriel proportionnel au gradient de température négatif dans l'objet. Pour être précis, le flux de chaleur est défini comme un champ vectoriel\(F = - k \nabla T\), où la constante k est la conductivité thermique de la substance à partir de laquelle l'objet est fabriqué (cette constante est déterminée expérimentalement). Le débit de chaleur à travers la surface S de l'objet est donné par l'intégrale du flux
\[\iint_S \vecs F \cdot dS = \iint_S -k \vecs \nabla T \cdot dS. \nonumber \]
Un cylindre plein en fonte est donné par les inégalités\(x^2 + y^2 \leq 1, \, 1 \leq z \leq 4\). La température au point\((x,y,z)\) dans une région contenant le cylindre est de\(T(x,y,z) = (x^2 + y^2)z\). Étant donné que la conductivité thermique de la fonte est de 55, déterminez le flux de chaleur à travers la limite du solide si cette limite est orientée vers l'extérieur.
Solution
\(S\)Dénotons la limite de l'objet. Pour déterminer le flux de chaleur, nous devons calculer l'intégrale du flux.\[\iint_S -k\vecs \nabla T \cdot dS. \nonumber \] Remarquez qu'il ne\(S\) s'agit pas d'une surface lisse mais lisse par morceaux, puisqu'\(S\)il s'agit de l'union de trois surfaces lisses (le haut et le bas circulaires et le côté cylindrique). Par conséquent, nous calculons trois intégrales distinctes, une pour chaque partie lisse de\(S\). Avant de calculer des intégrales, notez que le gradient de température est\(\vecs \nabla T = \langle 2xz, \, 2yz, \, x^2 + y^2 \rangle\).
Nous considérons d'abord le fond circulaire de l'objet, que nous désignons\(S_1\). Nous pouvons voir qu'il\(S_1\) s'agit d'un cercle de rayon 1 centré sur un point\((0,0,1)\) situé dans le plan\(z = 1\). Cette surface est paramétrée\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 1 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Par conséquent,
\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\)et\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle\), et\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0, \, 0, -v \rangle\).
Comme la surface est orientée vers l'extérieur et\(S_1\) constitue le bas de l'objet, il est logique que ce vecteur pointe vers le bas. Par équation, le flux de chaleur à travers\(S_1\) est
\[ \begin{align*}\iint_{S_1} -k \vecs \nabla T \cdot dS &= - 55 \int_0^{2\pi} \int_0^1 \vecs \nabla T(u,v) \cdot (\vecs t_u \times \vecs t_v) \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2 \cos^2 u + v^2 \sin^2 u \rangle \cdot \langle 0,0, -v\rangle \, dv \,du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2\rangle \cdot \langle 0, 0, -v \rangle \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 -v^3 \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} -\dfrac{1}{4} du \\[4pt] &= \dfrac{55\pi}{2}.\end{align*}\]
Considérons maintenant le sommet circulaire de l'objet, que nous désignons\(S_2\). Nous voyons qu'il\(S_2\) s'agit d'un cercle de rayon 1 centré en un point\((0,0,4)\), situé dans le plan\(z = 4\). Cette surface est paramétrée\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 4 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Donc,\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\) et\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle \), et\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0,0,-v\rangle\).
Puisque la surface est orientée vers l'extérieur et\(S_1\) constitue le sommet de l'objet, nous prenons plutôt un vecteur\(\vecs t_v \times \vecs t_u = \langle 0,0,v\rangle\). Par équation, le flux de chaleur à travers\(S_1\) est
\ [\ begin {align*} \ iint_ {S_2} -k \ vecs \ nabla T \ cdot dS &= - 55 \ int_0^ {2 \ pi} \ int_0^1 \ vecs \ nabla T (u, v) \ cdot \, (\ vecs t_u \ times \ vecs t_v) \, dv \, du \ \ [4pt]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 \ langle 8v \, \ cos u, \, 8v \, \ sin u, \, v^2 \ cos^2 u + v^2 \ sin^2 u \ rangle \ cdot \ langle 0,0, -v \ rangle \, dv \, du \ \ [4pt]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 \ angle 8v \, \ cos u, \, 8v \, \ sin u, \, v^2 \ rangle \ cdot \ langle 0, 0, -v \ rangle \, \, dv \, du \ \ [4 pt]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 -v^3 \, dv \, du = - 55 \ int_0^ {2 \ pi} - \ dfrac {1} {4} \, du = - \ dfrac {55 \ pi} {2}. \ end {align*} \]
Enfin, considérons le côté cylindrique de l'objet. Cette surface est paramétrée\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 1 \leq v \leq 4\). Par exemple, nous le savons\(\vecs t_u \times \vecs t_v = \langle \cos u, \, \sin u, \, 0 \rangle\). Par équation,
\ [\ begin {align*} \ iint_ {S_3} -k \ vecs \ nabla T \ cdot dS &= - 55 \ int_0^ {2 \ pi} \ int_1^4 \ vecs \ nabla T (u, v) \ cdot (\ vecs t_u \ times \ vecs t_v) \, dv \, du \ \ [4 points]
&= - 55 \ int_0^ {2 \ pi} \ int_1^4 \ langle 2v \, \ cos u, \, 2v \, \ sin u, \ cos^2 u + \ sin^2 u \ rangle \ cdot \ langle \ cos u, \, \ sin u, \, 0 \ rangle \, dv \, du \ \ [4pt]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 \ angle 2v \, \ cos^2 u, \, 2v \, \ sin u, \, 1 \ rangle \ cdot \ langle \ cos u, \, \ sin u, \, 0 \ rangle \, dv \, \, du \ \ [4 points]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 (2v \, \ cos^2 u + 2v \, \ sin^2 u) \, dv \, du \ \ [4 points]
&= - 55 \ int_0^ {2 \ pi} \ int_0^1 2v \, dv \, du \ \ [4 points]
&= -55 \ int_0^ {2 \ pi} du \ \ [4 points]
&= -110 \ pi. \ end {align*} \]
Par conséquent, le débit de chaleur à travers\(S\) est
\[\dfrac{55\pi}{2} - \dfrac{55\pi}{2} - 110\pi = -110\pi. \nonumber \]
Une boule solide en fonte est donnée par l'inégalité\(x^2 + y^2 + z^2 \leq 1\). La température en un point d'une région contenant la balle est de\(T(x,y,z) = \dfrac{1}{3}(x^2 + y^2 + z^2)\). Déterminez le flux de chaleur à travers la limite du solide si cette limite est orientée vers l'extérieur.
- Allusion
-
Suivez les étapes de l'exemple\(\PageIndex{15}\).
- Réponse
-
\(-\dfrac{440\pi}{3}\)
Concepts clés
- Les surfaces peuvent être paramétrées, tout comme les courbes peuvent être paramétrées. En général, les surfaces doivent être paramétrées avec deux paramètres.
- Les surfaces peuvent parfois être orientées, tout comme les courbes. Certaines surfaces, comme une bande de Möbius, ne peuvent pas être orientées.
- Une intégrale de surface est comme une intégrale linéaire dans une dimension supérieure. Le domaine d'intégration d'une intégrale de surface est une surface dans un plan ou un espace, plutôt qu'une courbe dans un plan ou un espace.
- L'entier d'une intégrale de surface peut être une fonction scalaire ou un champ vectoriel. Pour calculer une intégrale de surface avec un integrand qui est une fonction, utilisez l'équation. Pour calculer une intégrale de surface avec un integrand qui est un champ vectoriel, utilisez l'équation.
- S'il s'\(S\)agit d'une surface, alors la surface de\(S\) est\[\iint_S \, dS. \nonumber \]
Équations clés
- Une surface scalaire intégrale
\[\iint_S f(x,y,z) \,dS = \iint_D f (\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA \nonumber \]
- Flux intégral
\[\iint_S \vecs F \cdot \vecs N \, dS = \iint_S \vecs F \cdot dS = \iint_D \vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \nonumber \]
Lexique
- flux intégral
- un autre nom pour l'intégrale de surface d'un champ vectoriel ; terme préféré en physique et en ingénierie
- courbes du quadrillage
- courbes sur une surface qui sont parallèles aux lignes de la grille dans un plan de coordonnées
- flux de chaleur
- un champ vectoriel proportionnel au gradient de température négatif dans un objet
- flux de masse
- le débit massique d'un fluide par unité de surface, mesuré en masse par unité de temps par unité de surface
- orientation d'une surface
- si une surface possède un côté « intérieur » et un côté « extérieur », alors une orientation est un choix entre le côté intérieur ou le côté extérieur ; la surface peut également avoir des orientations « vers le haut » et « vers le bas »
- domaine des paramètres (espace des paramètres)
- la région du\(uv\) plan sur laquelle les paramètres\(u\) et B\(v\) varient pour le paramétrage\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\)
- surface paramétrée (surface paramétrique)
- une surface donnée par une description de la forme\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\), où les paramètres\(u\) et D\(v\) varient sur un domaine de paramètres dans le\(uv\) plan
- paramétrage régulier
- paramétrage\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\) tel qu'il ne\(r_u \times r_v\) soit pas nul pour un point\((u,v)\) dans le domaine du paramètre
- superficie
- l'aire de surface\(S\) donnée par l'intégrale de surface\[\iint_S \,dS \nonumber \]
- surface intégrale
- intégrale d'une fonction sur une surface
- intégrale de surface d'une fonction à valeur scalaire
- une intégrale de surface dans laquelle l'integrand est une fonction scalaire
- intégrale de surface d'un champ vectoriel
- une intégrale de surface dans laquelle l'integrand est un champ vectoriel



Il ressort de l'exemple\(\PageIndex{1}\) que nous pouvons paramétrer tous les cylindres du formulaire\(x^2 + y^2 = R^2\). Si S est un cylindre donné par une équation\(x^2 + y^2 = R^2\), alors un paramétrage de\(S\) est\(\vecs r(u,v) = \langle R \, \cos u, \, R \, \sin u, \, v \rangle, \, 0 \leq u \leq 2 \pi, \, -\infty < v < \infty.\)
Nous pouvons également trouver différents types de surfaces en fonction de leur paramétrage, ou nous pouvons trouver un paramétrage lorsque l'on nous donne une surface.
Exemple\(\PageIndex{2}\): Describing a Surface
Décrire la surface\(S\) paramétrée par\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u^2 \rangle, \, 0 \leq u < \infty, \, 0 \leq v < 2\pi\).
Solution
Notez que si elle\(u\) est maintenue constante, la courbe résultante est un cercle de rayon\(u\) dans le plan\(z = u\). Par conséquent, à mesure qu'il\(u\) augmente, le rayon du cercle résultant augmente. Si elle\(v\) est maintenue constante, la courbe résultante est une parabole verticale. Par conséquent, nous nous attendons à ce que la surface soit un paraboloïde elliptique. Pour confirmer cela, notez que
\[\begin{align*} x^2 + y^2 &= (u \, \cos v)^2 + (u \, \sin v)^2 \\[4pt] &= u^2 \cos^2 v + u^2 sin^2 v \\[4pt] &= u^2 \\[4pt] &=z\end{align*}\]
La surface est donc le paraboloïde elliptique\(x^2 + y^2 = z\) (Figure\(\PageIndex{3}\)).
Exercice\(\PageIndex{2}\)
Décrivez la surface paramétrée par\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, - \infty < u < \infty, \, 0 \leq v < 2\pi\).
Maintenez la\(u\) constante et voyez le type de courbes qui en résulte. Imaginez ce qui se passe lorsque vous\(u\) augmentez ou diminuez.
Cône\(x^2 + y^2 = z^2\)