Skip to main content
Global

16.6E : Exercices pour la section 16.6

  1. Last updated
  2. Save as PDF
  • Page ID
    197819

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 4, déterminez si les déclarations sont vraies ou fausses.

    1. Si la surface\(S\) est donnée par\(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}\), alors\(\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx \, dy.\)

    Réponse
    Vrai

    2. Si la surface\(S\) est donnée par\(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}\), alors\(\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx \, dy.\)

    3. La surface\(\vecs r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle,\) pour\( 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) est la même surface\(\vecs r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle,\) pour\( 0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4\).

    Réponse
    Vrai

    4. Compte tenu du paramétrage standard d'une sphère,\(t_u \times t_v\) les vecteurs normaux sont des vecteurs normaux sortants.

    Dans les exercices 5 à 10, trouvez des descriptions paramétriques pour les surfaces suivantes.

    5. Avion\(3x - 2y + z = 2\)

    Réponse
    \(\vecs r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle \)pour\(-\infty \leq u < \infty\) et\( - \infty \leq v < \infty\).

    6. Paraboloïde\(z = x^2 + y^2\), pour\(0 \leq z \leq 9\).

    7. Avion\(2x - 4y + 3z = 16\)

    Réponse
    \(\vecs r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle \)pour\(|u| < \infty\) et\(|v| < \infty\).

    8. Le tronc de cône\(z^2 = x^2 + y^2\), pour\(2 \leq z \leq 8\)

    9. La partie du cylindre\(x^2 + y^2 = 9\) dans le premier octant, pour\(0 \leq z \leq 3\)

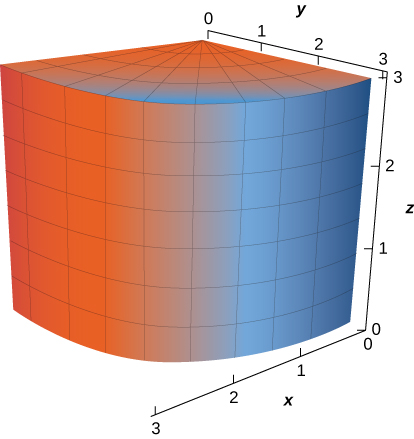
    Schéma en trois dimensions d'une section d'un cylindre de rayon 3. Le centre de son sommet circulaire est (0,0,3). La section existe pour x, y et z entre 0 et 3.

    Réponse
    \(\vecs r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle \) for \(0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3\)

    10. A cone with base radius \(r\) and height \(h,\) where \(r\) and \(h\) are positive constants.

    For exercises 11 - 12, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.

    11. [T] Half cylinder \(\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}\)

    Answer
    \(A = 87.9646\)

    12. [T] Plane \(z = 10 - z - y\) above square \(|x| \leq 2, \, |y| \leq 2\)

    In exercises 13 - 15, let \(S\) be the hemisphere \(x^2 + y^2 + z^2 = 4\), with \(z \geq 0\), and evaluate each surface integral, in the counterclockwise direction.

    13. \(\displaystyle \iint_S z\, dS\)

    Answer
    \(\displaystyle \iint_S z \, dS = 8\pi\)

    14. \(\displaystyle \iint_S (x - 2y) \, dS\)

    15. \(\displaystyle \iint_S (x^2 + y^2) \, dS\)

    Answer
    \(\displaystyle \iint_S (x^2 + y^2) \, dS = 16 \pi\)

    In exercises 16 - 18, evaluate \(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS\) for vector field \(\vecs F\) where \(\vecs N\) is an outward normal vector to surface \(S.\)

    16. \(\vecs F(x,y,z) = x\,\mathbf{\hat i}+ 2y\,\mathbf{\hat j} = 3z\,\mathbf{\hat k}\), and \(S\) is that part of plane \(15x - 12y + 3z = 6\) that lies above unit square \(0 \leq x \leq 1, \, 0 \leq y \leq 1\).

    17. \(\vecs F(x,y) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j}\), and \(S\) is hemisphere \(z = \sqrt{1 - x^2 - y^2}\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{4\pi}{3}\)

    18. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}\), and \(S\) is the portion of plane \(z = y + 1\) that lies inside cylinder \(x^2 + y^2 = 1\).

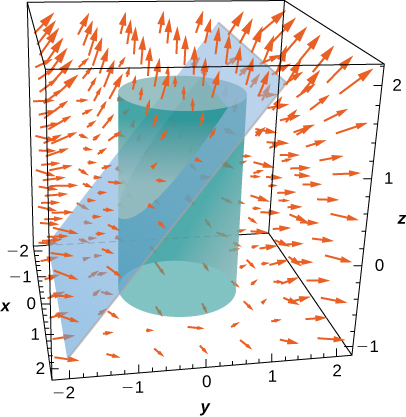
    A cylinder and an intersecting plane shown in three-dimensions. S is the portion of the plane z = y + 1 inside the cylinder x^2 + y ^2 = 1.

    Dans les exercices 19 à 20, approximez la masse de la lame homogène ayant la forme d'une surface donnée.\(S.\) Arrondissez à quatre décimales.

    19. [T]\(S\) est une surface\(z = 4 - x - 2y\), avec\(z \geq 0, \, x \geq 0, \, y \geq 0; \, \xi = x.\)

    Réponse
    \(m \approx 13.0639\)

    20. [T]\(S\) est une surface\(z = x^2 + y^2\), avec\(z \leq 1; \, \xi = z\).

    21. [T]\(S\) est une surface\(x^2 + y^2 + x^2 = 5\), avec\(z \geq 1; \, \xi = \theta^2\).

    Réponse
    \(m \approx 228.5313\)

    22. Évaluez\(\displaystyle \iint_S (y^2 z\,\mathbf{\hat i}+ y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}) \cdot dS,\) où\(S\) se trouve la surface du cube\(-1 \leq x \leq 1, \, -1 \leq y \leq 1\), et\(0 \leq z \leq 2\) dans le sens antihoraire.

    23. Évaluez l'intégrale de surface\(\displaystyle \iint_S g \, dS,\) où\(g(x,y,z) = xz + 2x^2 - 3xy\) et\(S\) est la partie du plan\(2x - 3y + z = 6\) située au-dessus de l'unité carrée\(R: 0 \leq x \leq 1, \, 0 \leq y \leq 1\).

    Réponse
    \(\displaystyle \iint_S g\,dS = 3 \sqrt{4}\)

    24. Évaluez\(\displaystyle \iint_S (x + y + z)\, dS,\) où\(S\) se trouve la surface définie paramétriquement par\(\vecs R(u,v) = (2u + v)\,\mathbf{\hat i} + (u - 2v)\,\mathbf{\hat j} + (u + 3v)\,\mathbf{\hat k}\) for\(0 \leq u \leq 1\) et\(0 \leq v \leq 2\).

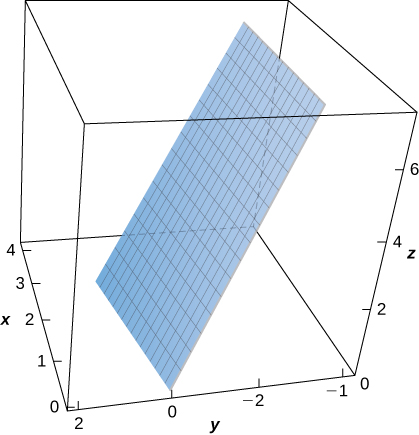
    Diagramme tridimensionnel de la surface donnée, qui semble être un plan fortement incliné s'étendant à travers le plan (x, y).

    25. [T] Évaluer\(\displaystyle \iint_S (x - y^2 + z)\, dS,\) where \(S\) is the surface defined parametrically by \(\vecs R(u,v) = u^2\,\mathbf{\hat i} + v\,\mathbf{\hat j} + u\,\mathbf{\hat k}\) for \(0 \leq u \leq 1, \, 0 \leq v \leq 1\).

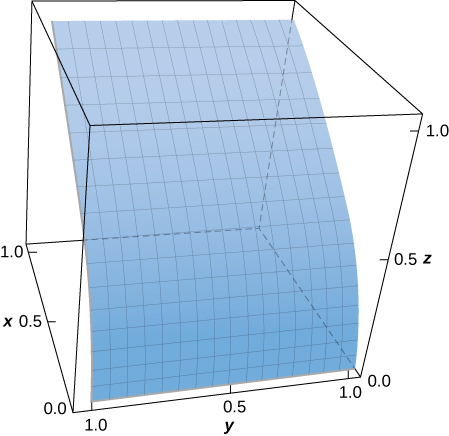
    A three-dimensional diagram of the given surface, which appears to be a curve with edges parallel to the y-axis. It increases in x components and decreases in z components the further it is from the y axis.

    Réponse
    \(\displaystyle \iint_S (x^2 + y - z) \, dS \approx 0.9617\)

    26. [T] Évaluez où\(S\) se trouve la surface définie par\(\vecs R(u,v) = u\,\mathbf{\hat i} - u^2\,\mathbf{\hat j} + v\,\mathbf{\hat k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1\) for\(0 \leq u \leq 1, \, 0 \leq v \leq 2\).

    27. Évaluez\(\displaystyle \iint_S (x^2 + y^2) \, dS,\) où\(S\) se trouve la surface délimitée au-dessus de l'hémisphère\(z = \sqrt{1 - x^2 - y^2}\) et en dessous par le plan\(z = 0\).

    Réponse
    \(\displaystyle \iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}\)

    28. Évaluez\(\displaystyle \iint_S (x^2 + y^2 + z^2) \, dS,\) où\(S\) se trouve la partie du plan située à l'intérieur du cylindre\(x^2 + y^2 = 1\).

    29. [T] Évaluez\(\displaystyle \iint_S x^2 z \, dS,\) où\(S\) se trouve la partie du cône\(z^2 = x^2 + y^2\) située entre les plans\(z = 1\) et\(z = 4\).

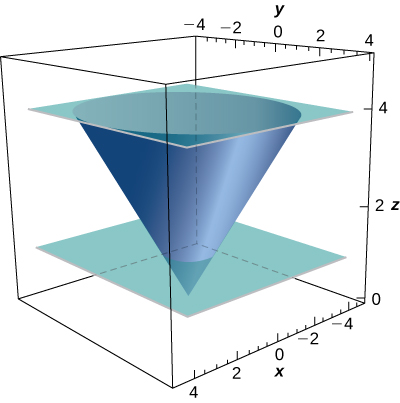
    Schéma du cône s'ouvrant vers le haut donné en trois dimensions. Le cône est coupé par les plans z=1 et z=4.

    Réponse
    \(\text{div}\,\vecs F = a + b\)

    \(\displaystyle \iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}\)

    30. [T] Evaluate \(\displaystyle \iint_S \frac{xz}{y} \, dS,\) where \(S\) is the portion of cylinder \(x = y^2\) that lies in the first octant between planes \(z = 0, \, z = 5\), and \(y = 4\).

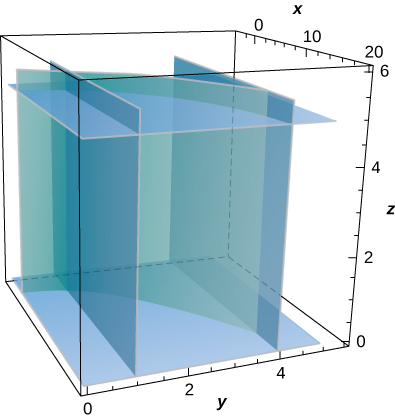
    A diagram of the given cylinder in three-dimensions. It is cut by the planes z=0, z=5, y=1, and y=4.

    31. [T] Évaluez\(\displaystyle \iint_S (z + y) \, dS,\) où se\(S\) trouve la partie du graphe située\( z = \sqrt{1 - x^2}\) dans le premier octant entre le\(xy\) plan et le plan\(y = 3\).

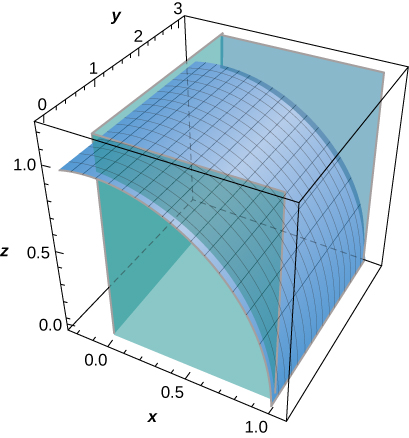
    Un diagramme de la surface donnée en trois dimensions dans le premier octant entre le plan xz et le plan y=3. Le graphe donné de z= la racine carrée de (1-x^2) s'étend vers le bas dans une courbe descendante concave allant du long (0, y,1) au long (1, y,0). Il ressemble à une partie d'un cylindre horizontal avec une base le long du plan xz et une hauteur le long de l'axe y.

    Réponse
    \(\displaystyle \iint_S (z + y) \, dS \approx 10.1\)

    32. Evaluate \(\displaystyle \iint_S xyz\, dS\) if \(S\) is the part of plane \(z = x + y\) that lies over the triangular region in the \(xy\)-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).

    33. Find the mass of a lamina of density \(\xi (x,y,z) = z\) in the shape of hemisphere \(z = (a^2 - x^2 - y^2)^{1/2}\).

    Answer
    \(m = \pi a^3\)

    34. Compute \(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} - 5y\,\mathbf{\hat j} + 4z\,\mathbf{\hat k}\) and \(\vecs N\) is an outward normal vector \(S,\) where \(S\) is the union of two squares \(S_1\) : \(x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) and \(S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1\).

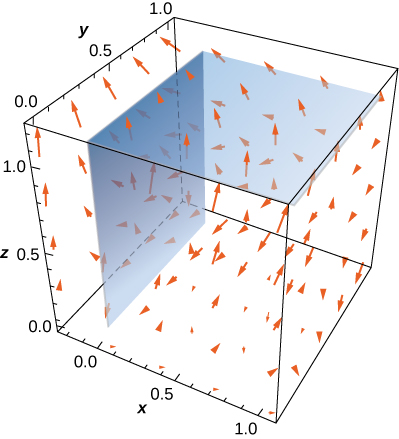
    A diagram in three dimensions. It shows the square formed by the components x=0, 0 <= y <= 1, and 0 <= z <= 1. It also shows the square formed by the components z=1, 0 <= x <= 1, and 0 <= y <= 1.

    35. Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) où\(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + z\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}\) et\(\vecs N\) est un vecteur normal vers l'extérieur\(S,\) où\(S\) est la région triangulaire coupée du plan\(x + y + z = 1\) par les axes de coordonnées positifs.

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{13}{24}\)

    36. Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) où\(\vecs F(x,y,z) = 2yz\,\mathbf{\hat i} + (\tan^{-1}xz)\,\mathbf{\hat j} + e^{xy}\,\mathbf{\hat k}\) et\(\vecs N\) est un vecteur normal vers l'extérieur\(S,\) où se\(S\) trouve la surface de la sphère\(x^2 + y^2 + z^2 = 1\).

    37. Calcule\(\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,\) où\(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + xyz\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}\) et\(\vecs N\) est un vecteur normal vers l'extérieur\(S,\) où se\(S\) trouve la surface des cinq faces du cube unitaire\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) manquante\(z = 0\).

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{3}{4}\)

    Pour les exercices 38 à 39, exprimez l'intégrale de surface sous la forme d'une intégrale double itérée en utilisant une projection\(S\) sur le\(yz\) plan.

    38. \(\displaystyle \iint_S xy^2 z^3 \, dS;\)\(S\)est la première partie octante du plan\(2x + 3y + 4z = 12\).

    39. \(\displaystyle \iint_S (x^2 - 2y + z) \, dS;\)\(S\)est la partie du graphe\(4x + y = 8\) délimitée par les plans de coordonnées et le plan\(z = 6\).

    Réponse
    \(\displaystyle \int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz \, dy\)

    Pour les exercices 40 à 41, exprimez l'intégrale de surface sous la forme d'une intégrale double itérée en utilisant une projection\(S\) sur le\(xz\) plan.

    40. \(\displaystyle \iint_S xy^2z^3 \, dS;\)\(S\)est la première partie octante du plan\(2x + 3y + 4z = 12\).

    41. \(\displaystyle \iint_S (x^2 - 2y + z) \, dS;\)est la partie du graphe\(4x + y = 8\) délimitée par les plans de coordonnées et le plan\(z = 6\).

    Réponse
    \(\displaystyle \int_0^2 \int_0^6 \big[x^2 - 2 (8 - 4x) + z\big] \sqrt{17} \, dz \, dx\)

    42. Évaluez l'intégrale de surface\(\displaystyle \iint_S yz \, dS,\) où\(S\) se trouve la première partie octante du plan\(x + y + z = \lambda\), où\(\lambda\) se trouve une constante positive.

    43. Évaluez l'intégrale de la surface\(\displaystyle \iint_S (x^2 z + y^2 z) \, dS,\) où\(S\) se trouve\(x^2 + y^2 + z^2 = a^2, \, z \geq 0.\)

    Réponse
    \(\displaystyle \iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}\)

    44. Évaluez l'intégrale de surface\(\displaystyle \iint_S z \, dA,\) où\(S\) se trouve la surface\(z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2\)

    45. Évaluez l'intégrale de la surface\(\displaystyle \iint_S x^2 yz \, dS,\) où se\(S\) trouve la partie du plan\(z = 1 + 2x + 3y\) située au-dessus du rectangle\(0 \leq x \leq 3\) et\(0 \leq y \leq 2\).

    Réponse
    \(\displaystyle \iint_S x^2 yz \, dS = 171 \sqrt{14}\)

    46. Évaluez l'intégrale de surface\(\displaystyle \iint_S yz \, dS,\) où\(S\)\(x + y + z = 1\) se trouve le plan situé dans le premier octant.

    47. Évaluez l'intégrale de surface\(\displaystyle \iint_S yz \, dS,\) où\(S\) se trouve la partie du plan\(z = y + 3\) située à l'intérieur du cylindre\(x^2 + y^2 = 1\).

    Réponse
    \(\displaystyle \iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}\)

    Pour les exercices 48 à 50, utilisez un raisonnement géométrique pour évaluer les intégrales de surface données.

    48. \(\displaystyle \iint_S \sqrt{x^2 + y^2 + z^2} \, dS,\)où se\(S\) trouve la surface\(x^2 + y^2 + z^2 = 4, \, z \geq 0\)

    49. \(\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS,\)où\(S\) est la surface\(x^2 + y^2 = 4, \, 1 \leq z \leq 3\), orientée avec des vecteurs normaux unitaires pointant vers l'extérieur

    Réponse
    \(\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS = 16 \pi\)

    50. \(\displaystyle \iint_S (z\,\mathbf{\hat k}) \cdot dS,\)où\(S\)\(x^2 + y^2 \leq 9\) le disque sur le plan est-il\(z = 4\) orienté avec les vecteurs normaux de l'unité pointant vers le

    51. Une lamelle a la forme d'une portion de sphère située à\(x^2 + y^2 + z^2 = a^2\) l'intérieur d'un cône\(z = \sqrt{x^2 + y^2}\). \(S\)Soit la coque sphérique centrée à l'origine avec le rayon a, et\(C\) soit le cône circulaire droit avec un sommet à l'origine et un axe de symétrie qui coïncide avec l'\(z\)axe. Déterminez la masse de la lame si\(\delta(x,y,z) = x^2 y^2 z\).

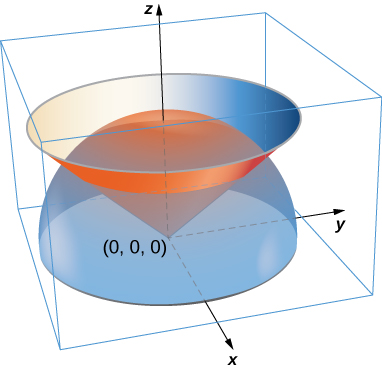
    Un schéma en trois dimensions. Un cône s'ouvre vers le haut avec un point à l'origine et un asic de symétrie qui coïncide avec l'axe Z. La moitié supérieure d'un hémisphère dont le centre est à l'origine s'ouvre vers le bas et est coupée par le plan xy.

    Réponse
    \(m = \dfrac{\pi a^7}{192}\)

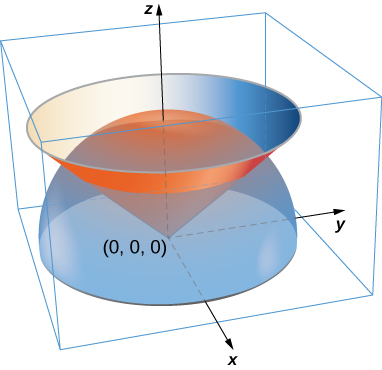
    52. A lamina has the shape of a portion of sphere \(x^2 + y^2 + z^2 = a^2\) that lies within cone \(z = \sqrt{x^2 + y^2}\). Let \(S\) be the spherical shell centered at the origin with radius a, and let \(C\) be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is \(\phi_0\), with \(0 \leq \phi_0 < \dfrac{\pi}{2}\). Determine the mass of that portion of the shape enclosed in the intersection of \(S\) and \(C.\) Assume \(\delta(x,y,z) = x^2y^2z.\)

    A diagram in three dimensions. A cone opens upward with point at the origin and an asic of symmetry that coincides with the z-axis. The upper half of a hemisphere with center at the origin opens downward and is cut off by the xy-plane.

    53. Un gobelet en papier a la forme d'un cône circulaire droit inversé d'une hauteur de 6 pouces et d'un rayon de 3 pouces en haut. Si la tasse est pleine d'eau pesée\(62.5 \, lb/ft^3\), déterminez l'ampleur de la force totale exercée par l'eau sur la surface intérieure de la tasse.

    Réponse
    \(F \approx 4.57 \, lb\)

    Pour les exercices 54 à 55, le champ vectoriel du flux thermique pour les objets conducteurs i\(\vecs F = - k\vecs\nabla T\), où\(T(x,y,z)\) est la température de l'objet et\(k > 0\) est une constante qui dépend du matériau. Déterminez le flux sortant\(\vecs F\) à travers les surfaces suivantes\(S\) pour les distributions de température données et supposez\(k = 1\).

    54. \(T(x,y,z) = 100 e^{-x-y}\);\(S\) se compose des faces d'un cube\(|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1\).

    55. \(T(x,y,z) = - \ln (x^2 + y^2 + z^2)\);\(S\) est une sphère\(x^2 + y^2 + z^2 = a^2\).

    Réponse
    \(8\pi a\)

    Pour les exercices 56 à 57, considérez les champs radiaux\(\vecs F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{\dfrac{p}{2}}} = \dfrac{r}{|r|^p}\), où\(p\) se trouve un nombre réel. \(S\)Constituées de sphères\(A\) et\(B\) centrées à l'origine avec des rayons\(0 < a < b\). Le flux sortant total à travers\(S\) se compose du flux sortant à travers la sphère extérieure\(B\) moins le flux entrant dans\(S\) la sphère intérieure.\(A.\)

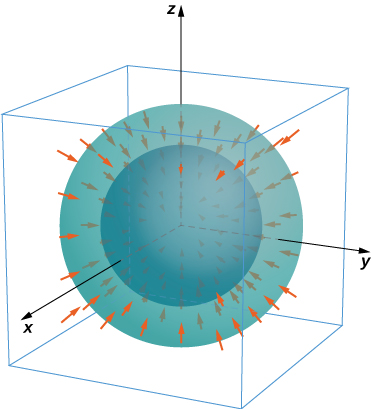
    Schéma en trois dimensions de deux sphères, l'une contenue complètement dans l'autre. Leurs centres en sont tous deux à l'origine. Les flèches pointent vers l'origine depuis l'extérieur des deux sphères.

    56. Trouvez le flux total à travers

    Template:ContribOpenStaxCalc