6.7: מעריכי מספרים שלמים וסימון מדעי

מטרות למידה

בסוף פרק זה תוכל:

• השתמש בהגדרה של מעריך שלילי
• פשט ביטויים עם מעריכי מספרים שלמים
• המר מסימון עשרוני לסימון מדעי
• המרת סימון מדעי לצורה עשרונית
• הכפל וחלק באמצעות סימון מדעי

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

1. מהו ערך המקום של 6 במספר 64891?
   אם פספסת בעיה זו, עיין בתרגיל 1.2.1.
2. תן שם לעשרוני: 0.0012.
   אם פספסת בעיה זו, עיין בתרגיל 1.8.1.
3. חיסור: 5− (-3).
   אם פספסת בעיה זו, סקור את תרגיל 1.4.33.

השתמש בהגדרה של מעריך שלילי

ראינו שלמאפיין המנה למעריכים שהוצג מוקדם יותר בפרק זה יש שתי צורות, תלוי אם המעריך גדול יותר במונה או במכנה.

נכס מנה למעריכים

אם a הוא מספר ממשי\(a\neq0\), ו- m ו- n הם מספרים שלמים, אז

\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]

ו

\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]

מה אם רק נחסר אקספונסנטים ללא קשר לאיזה גדול יותר?

בואו ניקח בחשבון\(\dfrac{x^{2}}{x^{5}}\).

אנו מחסרים את המעריך במכנה מהמעריך במונה.

\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]

אנו יכולים גם לפשט \(\dfrac{x^{2}}{x^{5}}\) על ידי חלוקת גורמים משותפים:

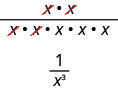
שלו מרמז על כך \(x^{-3}=\dfrac{1}{x^{3}}\) וזה מוביל אותנו להגדרה של אקספקטנט שלילי.

הגדרה: מעריך שלילי

אם n הוא מספר שלם\(a\neq 0\), ולאחר מכן \(a^{-n}=\dfrac{1}{a^{n}}\)

המעריך השלילי אומר לנו שנוכל לכתוב מחדש את הביטוי על ידי לקיחת ההדדיות של הבסיס ואז שינוי הסימן של המעריך.

כל ביטוי שיש לו אקספוננטים שליליים אינו נחשב בצורה הפשוטה ביותר. נשתמש בהגדרה של אקספוננט שלילי ותכונות אחרות של אקספונסנטים כדי לכתוב את הביטוי עם אקספוננטים חיוביים בלבד.

לדוגמה, אם לאחר פישוט ביטוי אנו בסופו של דבר עם הביטוי\(x^{-3}\), נעשה צעד נוסף ונכתוב\(\dfrac{1}{x^{3}}\). התשובה נחשבת בצורה הפשוטה ביותר כאשר יש לה רק אקספונסנטים חיוביים.

תרגיל \(\PageIndex{1}\)

פשט:

1. \(4^{-2}\)
2. \(10^{-3}\)

תשובה

1. \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
2. \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)

תרגיל \(\PageIndex{2}\)

פשט:

1. \(2^{-3}\)
2. \(10^{-7}\)

תשובה

1. \(\dfrac{1}{8}\)
2. \(\dfrac{1}{10^{7}}\)

תרגיל \(\PageIndex{3}\)

פשט:

1. \(3^{-2}\)
2. \(10^{-4}\)

תשובה

1. \(\dfrac{1}{9}\)
2. \(\dfrac{1}{10,000}\)

בתרגיל \(\PageIndex{1}\) העלינו מספר שלם למעריך שלילי. מה קורה כשאנחנו מעלים שבריר למעריך שלילי? נתחיל בבחינת מה קורה לשבר שהמונה שלו הוא אחד והמכנה שלו הוא מספר שלם שהועלה למעריך שלילי.

\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)

זה מוביל לנכס של אקספונסנטים שליליים.

תכונה של אקספונסנטים שליליים

אם n הוא מספר שלם\(a\neq 0\), ולאחר מכן\(\dfrac{1}{a^{-n}}=a^{n}\).

תרגיל \(\PageIndex{4}\)

פשט:

1. \(\dfrac{1}{y^{-4}}\)
2. \(\dfrac{1}{3^{-2}}\)

תשובה

1. \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
2. \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)

תרגיל \(\PageIndex{5}\)

פשט:

1. \(\dfrac{1}{p^{-8}}\)
2. \(\dfrac{1}{4^{-3}}\)

תשובה

1. \(p^{8}\)
2. 64

תרגיל \(\PageIndex{6}\)

פשט:

1. \(\dfrac{1}{q^{-7}}\)
2. \(\dfrac{1}{2^{-4}}\)

תשובה

1. \(q^{7}\)
2. 16

נניח שעכשיו יש לנו שבר שהועלה למעריך שלילי. בואו נשתמש בהגדרה שלנו של אקספונסנטים שליליים כדי להוביל אותנו לנכס חדש.

\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)

כדי להגיע מהשבר המקורי שהועלה למעריך שלילי לתוצאה הסופית, לקחנו את ההדדיות של הבסיס - השבר - ושינינו את סימן המעריך.

זה מוביל אותנו למנה לנכס כוח שלילי.

מנה לנכס אקספוננט שלילי

אם \(a\) \(b\) והם מספרים ממשיים, \(a \neq 0, b \neq 0,\) \(n\) והוא מספר שלם, אז \(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)

תרגיל \(\PageIndex{7}\)

פשט:

1. \(\left(\dfrac{5}{7}\right)^{-2}\)
2. \(\left(-\dfrac{2 x}{y}\right)^{-3}\)

תשובה

1. \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
2. \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)

תרגיל \(\PageIndex{8}\)

פשט:

1. \(\left(\dfrac{2}{3}\right)^{-4}\)
2. \(\left(-\dfrac{6 m}{n}\right)^{-2}\)

תשובה

1. \(\dfrac{81}{16} \)
2. \(\dfrac{n^{2}}{36 m^{2}}\)

תרגיל \(\PageIndex{9}\)

פשט:

1. \(\left(\dfrac{3}{5}\right)^{-3}\)
2. \(\left(-\dfrac{a}{2 b}\right)^{-4}\)

תשובה

1. \(\dfrac{125}{27}\)
2. \(\dfrac{16 b^{4}}{a^{4}}\)

כאשר מפשטים ביטוי עם אקספונסנטים, עלינו להקפיד לזהות נכון את הבסיס.

תרגיל \(\PageIndex{10}\)

פשט:

1. \((-3)^{-2}\)
2. \(-3^{-2}\)
3. \(\left(-\dfrac{1}{3}\right)^{-2}\)
4. \(-\left(\dfrac{1}{3}\right)^{-2}\)

תשובה

1. כאן המעריך חל על הבסיס -3. \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
2. הביטוי \(-3^{-2}\) פירושו "למצוא את ההפך מ\(3^{-2}\)". כאן המעריך חל על בסיס 3. \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
3. כאן המעריך חל על הבסיס\(\left(-\dfrac{1}{3}\right)\). \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
4. הביטוי \(-\left(\dfrac{1}{3}\right)^{-2}\) פירושו "למצוא את ההפך מ\(\left(\dfrac{1}{3}\right)^{-2}\)". כאן המעריך חל על הבסיס\(\left(\dfrac{1}{3}\right)\). \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)

תרגיל \(\PageIndex{11}\)

פשט:

1. \((-5)^{-2}\)
2. \(-5^{-2}\)
3. \(\left(-\dfrac{1}{5}\right)^{-2}\)
4. \(-\left(\dfrac{1}{5}\right)^{-2}\)

תשובה

1. \(\dfrac{1}{25}\)
2. \(-\dfrac{1}{25}\)
3. 25
4. −25

תרגיל \(\PageIndex{12}\)

פשט:

1. \((-7)^{-2}\)
2. \(-7^{-2}\)
3. \(\left(-\dfrac{1}{7}\right)^{-2}\)
4. \(-\left(\dfrac{1}{7}\right)^{-2}\)

תשובה

1. \(\dfrac{1}{49}\)
2. \(-\dfrac{1}{49}\)
3. 49
4. -49

עלינו להקפיד על ביצוע סדר הפעולות. בדוגמה הבאה, חלקים (א) ו- (ב) נראים דומים, אך התוצאות שונות.

תרגיל \(\PageIndex{13}\)

פשט:

1. 4 \(\cdot 2^{-1}\)
2. \((4 \cdot 2)^{-1}\)

תשובה

1. \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
2. \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)

תרגיל \(\PageIndex{14}\)

פשט:

1. 6 \(\cdot 3^{-1}\)
2. \((6 \cdot 3)^{-1}\)

תשובה

1. 2
2. \(\dfrac{1}{18}\)

תרגיל \(\PageIndex{15}\)

פשט:

1. 8 \(\cdot 2^{-2}\)
2. \((8 \cdot 2)^{-2}\)

תשובה

1. 2
2. \(\dfrac{1}{256}\)

כאשר משתנה מועלה למעריך שלילי, אנו מיישמים את ההגדרה באותה צורה שעשינו עם מספרים. נניח שכל המשתנים אינם אפס.

תרגיל \(\PageIndex{16}\)

פשט:

1. \(x^{-6}\)
2. \(\left(u^{4}\right)^{-3}\)

תשובה

1. \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
2. \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)

תרגיל \(\PageIndex{17}\)

פשט:

1. \(y^{-7}\)
2. \(\left(z^{3}\right)^{-5}\)

תשובה

1. \(\dfrac{1}{y^{7}}\)
2. \(\dfrac{1}{z^{15}}\)

תרגיל \(\PageIndex{18}\)

פשט:

1. \(p^{-9}\)
2. \(\left(q^{4}\right)^{-6}\)

תשובה

1. \(\dfrac{1}{p^{9}}\)
2. \(\dfrac{1}{q^{24}}\)

כשיש מוצר ומעריך עלינו להקפיד ליישם את האקספקטנט על הכמות הנכונה. על פי סדר הפעולות, אנו מפשטים ביטויים בסוגריים לפני החלת אקספונסנטים. נראה איך זה עובד בדוגמה הבאה.

תרגיל \(\PageIndex{19}\)

פשט:

1. 5 \(y^{-1}\)
2. \((5 y)^{-1}\)
3. \((-5 y)^{-1}\)

תשובה

1. \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
2. \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
3. \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)

תרגיל \(\PageIndex{20}\)

פשט:

1. 8 \(p^{-1}\)
2. \((8 p)^{-1}\)
3. \((-8 p)^{-1}\)

תשובה

1. \(\dfrac{8}{p}\)
2. \(\dfrac{1}{8 p}\)
3. \(-\dfrac{1}{8 p}\)

תרגיל \(\PageIndex{21}\)

פשט:

1. 11 \(q^{-1}\)
2. \((11 q)^{-1}-(11 q)^{-1}\)
3. \((-11 q)^{-1}\)

תשובה

1. \(\dfrac{11}{1 q}\)
2. \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
3. \(-\dfrac{1}{11 q}\)

עם אקספונסנטים שליליים, כלל המנה זקוק לצורה \(\dfrac{a^{m}}{a^{n}}=a^{m-n},\) אחת בלבד עבור 0. \(a \neq 0\) כאשר המעריך במכנה גדול מהמעריך במונה, מעריך המנה יהיה שלילי.

פשט ביטויים עם מעריכים שלמים

כל המאפיינים המעריכים שפיתחנו מוקדם יותר בפרק עם מעריכי מספר שלם חלים גם על מעריכי מספרים שלמים. אנו משחזרים אותם כאן לעיון.

סיכום מאפייני המעריך

אם \(a\) \(b\) והם מספרים ממשיים, \(m\) \(n\) והם מספרים שלמים, אז

\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)

תרגיל \(\PageIndex{22}\)

פשט:

1. \(x^{-4} \cdot x^{6}\)
2. \(y^{-6} \cdot y^{4}\)
3. \(z^{-5} \cdot z^{-3}\)

תשובה

1. \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
2. \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
3. \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)

תרגיל \(\PageIndex{23}\)

פשט:

1. \(x^{-3} \cdot x^{7}\)
2. \(y^{-7} \cdot y^{2}\)
3. \(z^{-4} \cdot z^{-5}\)

תשובה

1. \(x^{4}\)
2. \(\dfrac{1}{y^{5}}\)
3. \(\dfrac{1}{z^{9}}\)

תרגיל \(\PageIndex{24}\)

פשט:

1. \(a^{-1} \cdot a^{6}\)
2. \(b^{-8} \cdot b^{4}\)
3. \(c^{-8} \cdot c^{-7}\)

תשובה

1. \(a^{5}\)
2. \(\dfrac{1}{b^{4}}\)
3. \(\dfrac{1}{c^{15}}\)

בשתי הדוגמאות הבאות, נתחיל בשימוש במאפיין הקומוטטיבי כדי לקבץ את אותם משתנים יחד. זה מקל על זיהוי הבסיסים הדומים לפני השימוש במאפיין המוצר.

תרגיל \(\PageIndex{25}\)

פשט: \(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)

תשובה

\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)

תרגיל \(\PageIndex{26}\)

פשט: \(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)

תשובה

\(\frac{1}{p^3 q^3}\)

תרגיל \(\PageIndex{27}\)

פשט: \(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)

תשובה

\(\frac{1}{r^2 s^8}\)

אם למונומיאלים יש מקדמים מספריים, אנו מכפילים את המקדמים, בדיוק כמו שעשינו קודם.

תרגיל \(\PageIndex{28}\)

פשט: \(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)

תשובה

\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)

תרגיל \(\PageIndex{29}\)

פשט: \(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)

תשובה

\(-\frac{12v^5}{u}\)

תרגיל \(\PageIndex{30}\)

פשט: \(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)

תשובה

\(\frac{30d^3}{c^8}\)

בשתי הדוגמאות הבאות, נשתמש במאפיין הכוח ובמוצר לנכס כוח.

תרגיל \(\PageIndex{31}\)

פשט: \(\left(6 k^{3}\right)^{-2}\)

תשובה

\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)

תרגיל \(\PageIndex{32}\)

פשט: \(\left(-4 x^{4}\right)^{-2}\)

תשובה

\(\frac{1}{16x^8}\)

תרגיל \(\PageIndex{33}\)

פשט: \(\left(2 b^{3}\right)^{-4}\)

תשובה

\(\frac{1}{16b^{12}}\)

תרגיל \(\PageIndex{34}\)

פשט: \(\left(5 x^{-3}\right)^{2}\)

תשובה

\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)

תרגיל \(\PageIndex{35}\)

פשט: \(\left(8 a^{-4}\right)^{2}\)

תשובה

\(\frac{64}{a^8}\)

תרגיל \(\PageIndex{36}\)

פשט: \(\left(2 c^{-4}\right)^{3}\)

תשובה

\(\frac{8}{c^{12}}\)

כדי לפשט שבר, אנו משתמשים במאפיין Quotient ומחסירים את המעריכים.

תרגיל \(\PageIndex{37}\)

פשט: \(\dfrac{r^{5}}{r^{-4}}\)

תשובה

\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)

תרגיל \(\PageIndex{38}\)

פשט: \(\dfrac{x^{8}}{x^{-3}}\)

תשובה

\(x^{11}\)

תרגיל \(\PageIndex{39}\)

פשט: \(\dfrac{y^{8}}{y^{-6}}\)

תשובה

\(y^{14}\)

המר מסימון עשרוני לסימון מדעי

זוכר עבודה עם ערך מקום עבור מספרים שלמים עשרוניים? מערכת המספרים שלנו מבוססת על סמכויות של 10. אנו משתמשים בעשרות, מאות, אלפים וכן הלאה. המספרים העשרוניים שלנו מבוססים גם על כוחות של עשיריות - עשיריות, מאיות, אלפיות וכן הלאה. שקול את המספרים 4,000 ו 0.004. אנו יודעים כי 4,000 פירושו \(4 \times 1,000\) 0.004 פירושו\(4 \times \dfrac{1}{1,000}\).

אם נכתוב את 1000 ככוח של עשרה בצורה מעריכית, נוכל לשכתב את המספרים האלה בדרך זו:

\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]

כאשר מספר כתוב כתוצר של שני מספרים, כאשר הגורם הראשון הוא מספר גדול או שווה לאחד אך פחות מ -10, והגורם השני הוא כוח של 10 שנכתב בצורה מעריכית, אומרים שהוא נמצא בסימון מדעי.

סימון מדעי

מספר בא לידי ביטוי בסימון מדעי כאשר הוא בצורה

\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]

נהוג בסימון מדעי להשתמש כסימן \(\times\) הכפל, למרות שאנו נמנעים משימוש בסימן זה במקומות אחרים באלגברה.

אם נסתכל על מה שקרה לנקודה העשרונית, נוכל לראות שיטה להמרה בקלות מסימון עשרוני לסימון מדעי.

בשני המקרים, העשרוני הועבר 3 מקומות כדי לקבל את הגורם הראשון בין 1 ל -10.

\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)

תרגיל \(\PageIndex{40}\): HOW TO CONVERT FROM DECIMAL NOTATION TO SCIENTIFIC NOTATION

כתוב בסימון מדעי: 37000.

תשובה

תרגיל \(\PageIndex{41}\)

כתוב בסימון מדעי: 96000.

תשובה

\(9.6 \times 10^{4}\)

תרגיל \(\PageIndex{42}\)

כתוב בסימון מדעי: 48300.

תשובה

\(4.83 \times 10^{4}\)

כיצד: המר מסימון עשרוני לסימון מדעי

1. שלב 1. הזז את הנקודה העשרונית כך שהגורם הראשון יהיה גדול או שווה ל- 1 אך פחות מ- 10.
2. שלב 2. ספר את מספר המקומות העשרוניים, n, שהנקודה העשרונית הועברה.
3. שלב 3. כתוב את המספר כמוצר עם כוח של 10.
   אם המספר המקורי הוא:
   • גדול מ 1, את הכוח של 10 יהיה 10 ⁿ.
   • בין 0 ל -1, ההספק של 10 יהיה 10 ⁻ⁿ.
4. שלב 4. בדוק.

תרגיל \(\PageIndex{43}\)

כתוב בסימון מדעי: 0.0052.

תשובה

המספר המקורי, 0.0052, הוא בין 0 ל -1 כך שיהיה לנו כוח שלילי של 10.

הזז את הנקודה העשרונית כדי לקבל 5.2, מספר בין 1 ל -10.
ספור את מספר המקומות העשרוניים שהנקודה הועברה.
כתוב כמוצר עם כוח של 10.
בדוק.
\(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\)
0.0052

תרגיל \(\PageIndex{44}\)

כתוב בסימון מדעי: 0.0078

תשובה

\(7.8 \times 10^{-3}\)

תרגיל \(\PageIndex{45}\)

כתוב בסימון מדעי: 0.0129

תשובה

\(1.29 \times 10^{-2}\)

המרת סימון מדעי לצורה עשרונית

כיצד נוכל להמיר מסימון מדעי לצורה עשרונית? בואו נסתכל על שני מספרים שנכתבו בסימון מדעי ונראה.

\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]

אם נסתכל על המיקום של הנקודה העשרונית, נוכל לראות שיטה קלה להמיר מספר מסימון מדעי לצורה עשרונית.

\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]

בשני המקרים הנקודה העשרונית עברה 4 מקומות. כאשר המעריך היה חיובי, העשרוני עבר ימינה. כאשר המעריך היה שלילי, הנקודה העשרונית עברה שמאלה.

תרגיל \(\PageIndex{46}\)

המר לצורה עשרונית: \(6.2 \times 10^{3}\)

תשובה

תרגיל \(\PageIndex{47}\)

המר לצורה עשרונית: \(1.3 \times 10^{3}\)

תשובה

\(1,300\)

תרגיל \(\PageIndex{48}\)

המר לצורה עשרונית: \(9.25 \times 10^{4}\)

תשובה

\(92,500\)

השלבים מסוכמים להלן.

איך

המרת סימון מדעי לצורה עשרונית.

כדי להמיר סימון מדעי לצורה עשרונית:

1. שלב 1. קבע את המעריך,\(n\), על הגורם\(10\).
2. שלב 2. הזז את \(n\) המקומות העשרוניים, הוסף אפסים במידת הצורך.
   • אם המעריך חיובי, הזז את נקודות הנקודה \(n\) העשרונית ימינה.
   • אם המעריך שלילי, הזז את נקודות הנקודה \(|n|\) העשרונית שמאלה.
3. שלב 3. בדוק.

תרגיל \(\PageIndex{49}\)

המר לצורה עשרונית: \(8.9\times 10^{-2}\)

תשובה

קבע את המעריך,\(n\), על הגורם\(10\).
מכיוון שהמעריך שלילי, הזז את הנקודה העשרונית 2 מקומות שמאלה.
הוסף אפסים לפי הצורך עבור מצייני מיקום.

תרגיל \(\PageIndex{50}\)

המר לצורה עשרונית: \(1.2 \times 10^{-4}\)

תשובה

\(0.00012\)

תרגיל \(\PageIndex{51}\)

המר לצורה עשרונית: \(7.5 \times 10^{-2}\)

תשובה

\(0.075\)

הכפל וחלק באמצעות סימון מדעי

אסטרונומים משתמשים במספרים גדולים מאוד כדי לתאר מרחקים ביקום וגילאים של כוכבים וכוכבי לכת. כימאים משתמשים במספרים קטנים מאוד כדי לתאר את גודל האטום או המטען על אלקטרון. כאשר מדענים מבצעים חישובים עם מספרים גדולים מאוד או קטנים מאוד, הם משתמשים בסימון מדעי. סימון מדעי מספק דרך לביצוע החישובים מבלי לכתוב הרבה אפסים. נראה כיצד משתמשים בתכונות של אקספוננטים כדי להכפיל ולחלק מספרים בסימון מדעי.

תרגיל \(\PageIndex{52}\)

להכפיל. כתוב תשובות בצורה עשרונית: \(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)

תשובה

\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)

תרגיל \(\PageIndex{53}\)

להכפיל\((3\times 10^{6})(2\times 10^{-8})\). כתוב תשובות בצורה עשרונית.

תשובה

\(0.06\)

תרגיל \(\PageIndex{54}\)

להכפיל\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\). כתוב תשובות בצורה עשרונית.

תשובה

\(0.009\)

תרגיל \(\PageIndex{55}\)

לחלק. כתוב תשובות בצורה עשרונית: \(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)

תשובה

\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)

תרגיל \(\PageIndex{56}\)

חלק \(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\) כתוב תשובות בצורה עשרונית.

תשובה

\(400,000\)

תרגיל \(\PageIndex{57}\)

חלק \(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\) כתוב תשובות בצורה עשרונית.

תשובה

\(20,000\)

גישה למדיה למשאבים מקוונים נוספים

גש למשאבים מקוונים אלה להדרכה ותרגול נוספים עם מעריכים שלמים וסימון מדעי:

• אקספונסנטים שליליים
• סימון מדעי
• סימון מדעי 2

מושגי מפתח

• רכוש של אקספוננטים שליליים
  • אם \(n\) הוא מספר שלם חיובי\(a \ne 0\), ולאחר מכן \(\dfrac{1}{a^{−n}}=a^n\)
    
• מנה למעריך שלילי
  • אם \(a\) \(b\) והם מספרים ממשיים, \(b \ne 0\) \(n\) והוא מספר שלם, אז \(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
    
• כדי להמיר סימון מדעי לצורה עשרונית:
  1. קבע את המעריך, \(n\) על הגורם\(10\).
  2. הזז את \(n\) המקומות העשרוניים, הוסף אפסים במידת הצורך.
     • אם המעריך חיובי, הזז את נקודות הנקודה \(n\) העשרונית ימינה.
     • אם המעריך שלילי, הזז את נקודות הנקודה \(|n|\) העשרונית שמאלה.
  3. בדוק.
     
• כדי להמיר עשרוני לסימון מדעי:
  1. הזז את הנקודה העשרונית כך שהגורם הראשון יהיה גדול או שווה ל- \(1\) אך פחות מ\(10\).
  2. ספור את מספר המקומות העשרוניים, \(n\) שהנקודה העשרונית הועברה.
  3. כתוב את המספר כמוצר עם כוח של\(10\). אם המספר המקורי הוא:
     • גדול מ\(1\), כוחו של \(10\) הרצון יהיה \(10^n\)
     • בין \(0\) לבין\(1\), כוחו של \(10\) הרצון \(10^{−n}\)
  4. בדוק.

רשימת מילים

אקספקטנט שלילי

אם \(n\) הוא מספר שלם חיובי\(a \neq 0\), ולאחר מכן\(a^{-n}=\dfrac{1}{a^{n}}\).

סימון מדעי

מספר מתבטא בסימון מדעי כאשר הוא מהצורה \(a \times 10^{n}\) שבה \(a \geq 1\) ו- a <10 \(n\) והוא מספר שלם.