10.5: Graphing Quadratic equations

Last updated

Nov 1, 2022
Page ID
177462
Save as PDF
- 10.4E: Mazoezi
- 10.5E: Mazoezi

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Tambua grafu ya equation ya quadratic katika vigezo viwili
Pata mhimili wa ulinganifu na vertex ya parabola
Find intercepts ya parabola
Grafu equations quadratic katika vigezo viwili
Tatua maombi ya kiwango cha juu na cha chini

Kuwa tayari

Kabla ya kuanza, fanya jaribio hili la utayari.

Grafu equation $y=3x−5$ kwa pointi njama.
Ikiwa umekosa tatizo hili, tathmini [kiungo].
Tathmini $2x^2+4x−1$ wakati $x=−3$
Kama amekosa tatizo hili, mapitio [kiungo].
Tathmini $−\frac{b}{2a}$ wakati $a=13$ na b= $\frac{5}{6}$
Ikiwa umekosa tatizo hili, tathmini [kiungo].

Tambua Grafu ya Equation ya Quadratic katika Vigezo viwili

Tuna graphed equations ya fomu $Ax+By=C$ . Sisi kuitwa equations kama equations hii linear kwa sababu grafu yao ni mistari moja kwa moja.

Sasa, sisi grafu equations ya fomu $y=ax^2+bx+c$ . Tunaita aina hii ya equation equation quadratic katika vigezo mbili.

ufafanuzi: QUADRATIC EQUATION KATIKA VIGEZO MBILI

equation quadratic katika vigezo mbili, ambapo a, b, na c ni namba halisi na $a\neq 0$ , ni equation ya fomu

$y=ax^2+bx+c \nonumber$

Tu kama sisi kuanza graphing equations linear na pointi njama, tutafanya hivyo kwa equations quadratic.

Hebu tuangalie kwanza kwenye kuchora equation ya quadratic $y=x^2$ . Tutachagua maadili integer ya x kati ya -1 na 2 na kupata maadili yao y. Angalia Jedwali.

$y=x^2$
x	y
0	0
1	1
$−1$	1
2	4
$−2$	4

Taarifa wakati sisi basi $x=1$ na $x=−1$ , tulipata thamani sawa kwa y.

$\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}$

Kitu kimoja kilichotokea wakati sisi basi $x=2$ na $x=−2$ .

Sasa, tutapanga pointi ili kuonyesha grafu ya $y=x^2$ . Angalia Kielelezo.

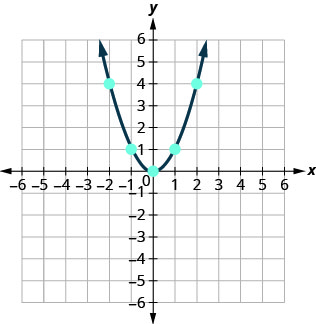
Takwimu hii inaonyesha upward-ufunguzi u umbo Curve graphed juu ya x y-kuratibu ndege. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. hatua ya chini kabisa juu ya Curve ni katika hatua (0, 0). Vipengele vingine kwenye safu ziko kwenye (-2, 4), (-1, 1), (1, 1) na (2, 4).

Grafu sio mstari. Takwimu hii inaitwa parabola. Kila equation quadratic ina grafu inayoonekana kama hii.

Katika Mfano utakuwa mazoezi graphing parabola kwa kupanga pointi chache.

Mfano $\PageIndex{1}$

$y=x^2-1$

Jibu

Tutaweka graph equation kwa pointi za kupanga.

Chagua maadili integers kwa x, badala yao katika equation na kutatua kwa y.
Rekodi maadili ya jozi zilizoamriwa kwenye chati.		$.$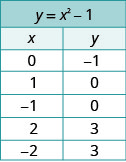
Panda pointi, kisha uunganishe na safu ya laini. Matokeo yake yatakuwa grafu ya equation $y=x^2−1$		$.$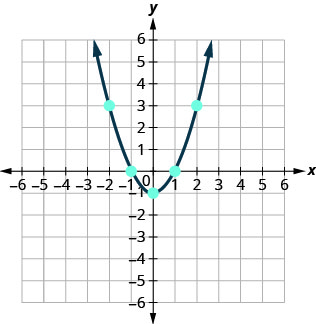

Mfano $\PageIndex{2}$

Grafu $y=−x^2$ .

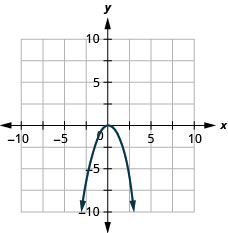
Jibu: $Takwimu hii inaonyesha chini-kufungua u umbo Curve graphed juu ya x y-kuratibu ndege. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. hatua ya juu juu ya Curve ni katika hatua (0, 0). Vipengele vingine kwenye safu ziko kwenye (-2, -4), (-1, -1), (1, -1) na (2, -4).$

Mfano $\PageIndex{3}$

Grafu $y=x^2+1$ .

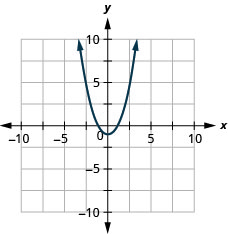
Jibu: $Takwimu hii inaonyesha upward-ufunguzi u umbo Curve graphed juu ya x y-kuratibu ndege. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. hatua ya chini kabisa juu ya Curve ni katika hatua (0, 1). Vipengele vingine kwenye safu ziko kwenye (-2, 5), (-1, 2), (1, 2) na (2, 5).$

Jinsi ya kufanya equations $y=x^2$ na $y=x^2−1$ differ? What is the difference between their graphs? How are their graphs the same?

Vipengele vyote vya fomu $y=ax^2+bx+c$ hufungua juu au chini. Angalia Kielelezo.

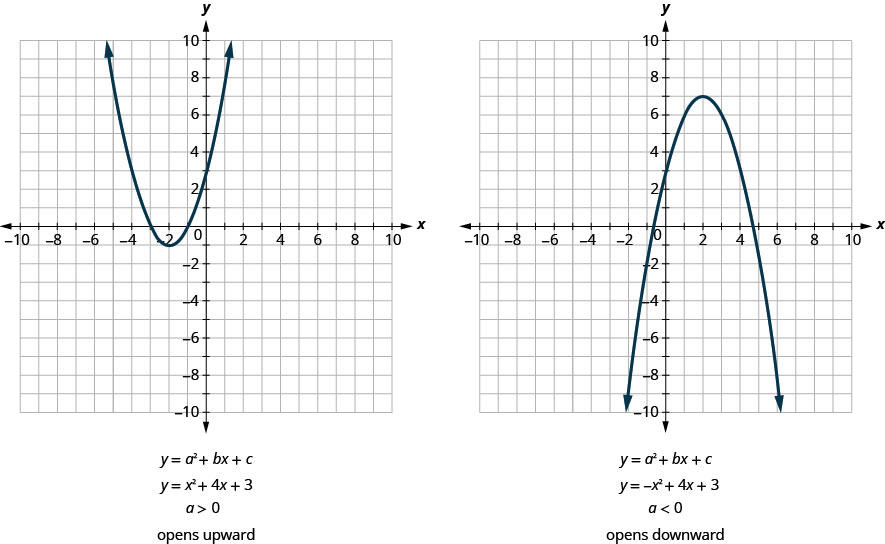
Takwimu hii inaonyesha grafu mbili kwa upande. Grafu upande wa kushoto inaonyesha safu ya juu ya kufungua u iliyofunikwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hatua ya chini kabisa kwenye safu iko kwenye hatua (-2, -1). Vipengele vingine kwenye safu ziko kwenye (-3, 0), na (-1, 0). Chini ya grafu ni equation y sawa na squared pamoja b x plus c Chini hiyo ni equation ya grafu, y sawa x squared pamoja 4 x plus 3. Chini hiyo ni ukosefu wa usawa mkubwa kuliko 0 ambayo inamaanisha parabola inafungua zaidi. Grafu upande wa kulia inaonyesha curve ya chini ya kufungua u iliyofunikwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. hatua ya juu juu ya Curve ni katika hatua (2, 7). Vipengele vingine kwenye pembe ziko kwenye (0, 3), na (4, 3). Chini ya grafu ni equation y sawa na squared pamoja b x plus c Chini hiyo ni equation ya grafu, y sawa na hasi x squared pamoja 4 x pamoja 3. Chini hiyo ni usawa chini ya 0 ambayo inamaanisha parabola inafungua chini.

Kumbuka kwamba tofauti tu katika equations mbili ni ishara hasi kabla ya $x^2$ katika equation ya grafu ya pili katika Kielelezo. Wakati $x^2$ neno ni chanya, parabola inafungua juu, na wakati $x^2$ neno ni hasi, parabola inafungua chini.

Ufafanuzi: PARABOLA ORIEN

Kwa equation quadratic $y=ax^2+bx+c$ , kama:

$Picha inaonyesha kauli mbili. Taarifa ya kwanza inasoma “kubwa kuliko 0, parabola inafungua juu”. Kauli hii inafuatiwa na picha ya parabola ya ufunguzi wa juu. Taarifa ya pili inasoma “chini ya 0, parabola inafungua chini”. Kauli hii inafuatiwa na picha ya parabola ya ufunguzi wa chini.$

Mfano $\PageIndex{4}$

Kuamua kama kila parabola inafungua juu au chini:

$y=−3x^2+2x−4$
$y=6x^2+7x−9$

Jibu

$.$

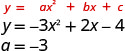
Kwa kuwa “a” ni hasi, parabola itafungua chini.

$.$

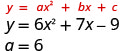
Kwa kuwa “a” ni chanya, parabola itafungua juu.

Mfano $\PageIndex{5}$

Kuamua kama kila parabola inafungua juu au chini:

$y=2x^2+5x−2$
$y=−3x^2−4x+7$

Jibu

juu
chini

Mfano $\PageIndex{6}$

Kuamua kama kila parabola inafungua juu au chini:

$y=−2x^2−2x−3$
$y=5x^2−2x−1$

Jibu

chini
juu

Kupata Axis ya Ulinganifu na Vertex ya Parabola

Angalia tena kwenye Kielelezo. Je, unaweza kuona kwamba tunaweza mara kila parabola katika nusu na kwamba upande mmoja ingekuwa uongo juu ya nyingine? 'Mstari wa fold' ni mstari wa ulinganifu. Tunaiita mhimili wa ulinganifu wa parabola.

Tunaonyesha grafu mbili sawa tena na mhimili wa ulinganifu katika nyekundu. Angalia Kielelezo.

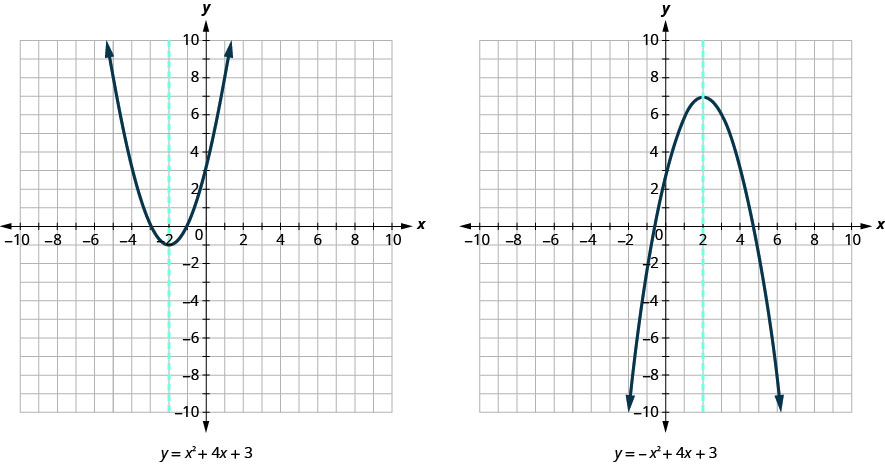
Takwimu hii inaonyesha grafu mbili kwa upande. Grafu upande wa kushoto inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hatua ya chini kabisa kwenye safu iko kwenye hatua (-2, -1). Vipengele vingine kwenye safu ziko kwenye (-3, 0), na (-1, 0). Pia kwenye grafu ni mstari wa wima uliopigwa ambao hupitia katikati ya parabola kwenye hatua (-2, -1). Chini ya grafu ni equation ya grafu, y sawa x squared pamoja 4 x plus 3. Grafu upande wa kulia inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. hatua ya juu juu ya Curve ni katika hatua (2, 7). Vipengele vingine kwenye pembe ziko kwenye (0, 3), na (4, 3). Pia kwenye grafu ni mstari wa wima uliopigwa ambao hupitia katikati ya parabola kwenye hatua (2, 7). Chini ya grafu ni equation ya grafu, y sawa na hasi x squared pamoja 4 x pamoja 3.

Ulinganisho wa mhimili wa ulinganifu unaweza kupatikana kwa kutumia Mfumo wa Quadratic. Tutaondoa derivation hapa na kuendelea moja kwa moja kutumia matokeo. Equation ya mhimili wa ulinganifu wa grafu ya $y=ax^2+bx+c$ ni x= $−\frac{b}{2a}$ .

Hivyo, ili kupata equation ya ulinganifu wa kila moja ya parabolas sisi graphed hapo juu, sisi badala katika formula x = $−\frac{b}{2a}$ .

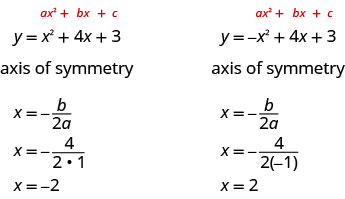
Takwimu inaonyesha hatua za kupata mhimili wa ulinganifu kwa parabolas mbili. Kwenye upande wa kushoto fomu ya kiwango cha equation ya quadratic ambayo ni y sawa na x squared plus b x plus c imeandikwa juu ya equation iliyotolewa y sawa x squared pamoja 4 x plus 3. Mhimili wa ulinganifu ni equation x sawa hasi b kugawanywa na wingi mara mbili a kuziba katika maadili ya a na b kutoka equation quadratic formula inakuwa x sawa hasi 4 kugawanywa na wingi mara 2 1, ambayo simplifies kwa x sawa hasi 2. Kwenye upande wa kulia fomu ya kiwango cha equation ya quadratic ambayo ni y sawa na x squared pamoja b x plus c imeandikwa juu ya equation iliyotolewa y sawa x squared pamoja 4 x plus 3. Mhimili wa ulinganifu ni equation x sawa hasi b kugawanywa na wingi mara mbili a kuziba katika maadili ya a na b kutoka equation quadratic formula inakuwa x sawa hasi 4 kugawanywa na wingi mara 2 -1, ambayo simplifies kwa x sawa 2. — Kielelezo. Je, haya ni equations ya mistari nyekundu iliyopigwa?

Hatua juu ya parabola ambayo ni juu ya mhimili wa ulinganifu ni hatua ya chini au ya juu juu juu ya parabola, kulingana na kama parabola inafungua juu au chini. Hatua hii inaitwa vertex ya parabola.

Tunaweza kupata urahisi kuratibu ya vertex, kwa sababu tunajua ni juu ya mhimili wa ulinganifu. Hii ina maana yake x -kuratibu ni $−\frac{b}{2a}$ . Ili kupata y -kuratibu ya vertex, sisi badala ya thamani ya x -kuratibu katika equation quadratic.

$Takwimu inaonyesha hatua za kupata vertex kwa parabolas mbili. Kwenye upande wa kushoto ni equation kupewa y sawa x squared pamoja 4 x plus 3. Chini ya equation ni kauli “mhimili wa ulinganifu ni x sawa -2”. Chini hiyo ni kauli “kipeo ni” karibu na taarifa ni jozi iliyoamriwa na x-thamani ya -2, sawa na mhimili wa ulinganifu, na thamani ya y ni tupu. Chini ya kuwa equation ya awali imeandikwa upya. Chini ya equation ni equation na -2 imechomekwa kwa thamani x ambayo ni y sawa -2 squared pamoja mara 4 -2 pamoja 3. Hii simplifies kwa y sawa -1. Chini ya hii ni taarifa “vertex ni (-2, -1)”. Kwenye upande wa kulia ni equation kupewa y sawa hasi x squared pamoja 4 x plus 3. Chini ya equation ni kauli “mhimili wa ulinganifu ni x sawa 2”. Chini hiyo ni kauli “kipeo ni” karibu na taarifa ni jozi iliyoamriwa na x-thamani ya 2, sawa na mhimili wa ulinganifu, na thamani ya y ni tupu. Chini ya kuwa equation ya awali imeandikwa upya. Chini equation ni equation na 2 imechomekwa kwa thamani x ambayo ni y sawa hasi wingi 2 squared, pamoja 4 mara 2 pamoja 3. Hii simplifies kwa y sawa 7. Chini ya hii ni kauli “vertex ni (2, 7)”.$

Ufafanuzi: AXIS YA ULINGANIFU NA VERTEX YA PARABOLA

Kwa parabola na equation $y=ax^2+bx+c$ :

Mhimili wa ulinganifu wa parabola ni mstari x= $−\frac{b}{2a}$ .
Vertex iko kwenye mhimili wa ulinganifu, hivyo x -kuratibu yake ni $−\frac{b}{2a}$ .

Ili kupata y -kuratibu ya vertex, sisi badala x= $−\frac{b}{2a}$ katika equation quadratic.

Mfano $\PageIndex{7}$

Kwa parabola $y=3x^2−6x+2$ kupata:

mhimili wa ulinganifu na
kipeo.

Jibu

1.		$.$
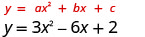
Mhimili wa ulinganifu ni mstari x= $−\frac{b}{2a}$		$.$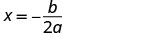
Badilisha maadili ya a, b katika equation.		$.$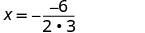
Rahisisha		x=1
		Mhimili wa ulinganifu ni mstari x=1
2.		$.$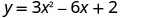
Vertex iko kwenye mstari wa ulinganifu, hivyo x -kuratibu yake itakuwa x=1
Mbadala x=1 katika equation na kutatua kwa y.		$.$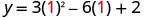
Rahisisha		$.$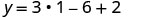
Hii ni y -kuratibu.		y=-1 Kipeo ni (1, -1).

Mfano $\PageIndex{8}$

Kwa parabola $y=2x^2−8x+1$ kupata:

mhimili wa ulinganifu na
kipeo.

Jibu

x=2
(2, -7)

Mfano $\PageIndex{9}$

Kwa parabola $y=2x^2−4x−3$ kupata:

mhimili wa ulinganifu na
kipeo.

Jibu

x=1
(1, -5)

Kupata Intercepts ya Parabola

Wakati sisi graphed equations linear, sisi mara nyingi kutumika x - na y -intercepts kutusaidia graph mistari. Kupata kuratibu za intercepts itatusaidia grafu parabolas, pia.

Kumbuka, katika y -intercept thamani ya x ni sifuri. Hivyo, ili kupata y -intercept, sisi badala x = 0 katika equation.

Hebu tupate y -intercepts ya parabolas mbili inavyoonekana katika takwimu hapa chini.

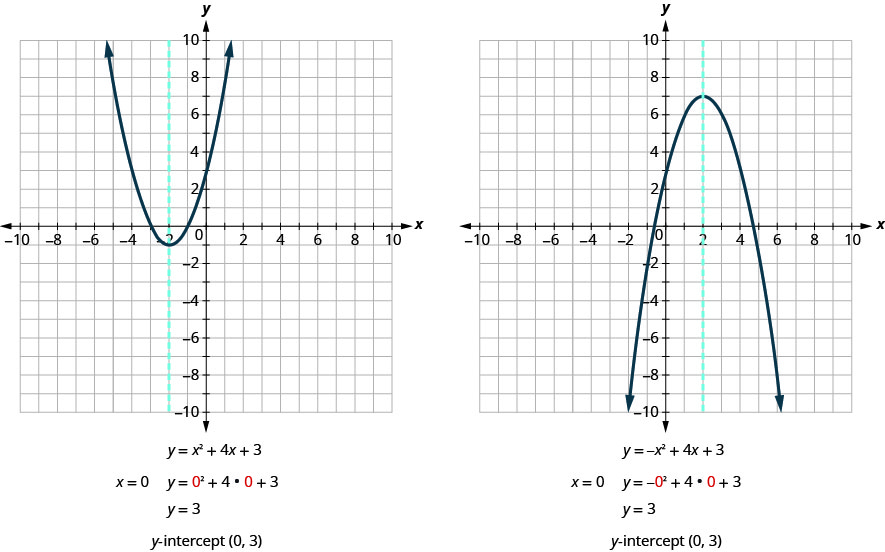
Katika x -intercept, thamani ya y ni sifuri. Ili kupata x -intercept, sisi badala $y=0$ katika equation. Kwa maneno mengine, tutahitaji kutatua equation $0=ax^2+bx+c$ kwa x.

$\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}$

Lakini kutatua equations quadratic kama hii ni nini hasa tumefanya mapema katika sura hii.

Sasa tunaweza kupata x -intercepts ya parabolas mbili inavyoonekana katika Kielelezo.

Kwanza, tutapata x -intercepts ya parabola na equation $y=x^2+4x+3$ .

		$.$
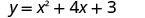Hebu y=0		$.$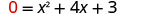
Sababu.		$.$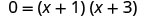
Tumia mali ya bidhaa ya sifuri.		$.$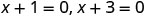
Kutatua.		$.$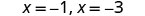
		Vipindi vya x ni (-1,0) na (-3,0).

Sasa, tutapata x -intercepts ya parabola na equation $y=−x^2+4x+3$ .

		$.$
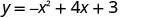Hebu y=0		$.$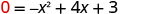
Quadratic hii haina sababu, kwa hiyo tunatumia Mfumo wa Quadratic.		$.$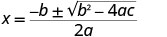
a=-1, b=4, c=3.		$.$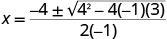
Kurahisisha.		$.$ $.$ $.$ $.$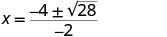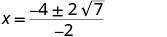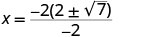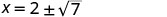
		Ya x intercepts ni $(2+\sqrt{7},0)$ na $(2−\sqrt{7},0)$

Tutatumia makadirio decimal ya x-intercepts, ili tuweze Machapisho pointi hizi kwenye grafu.

$\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}$

Je, matokeo haya yanakubaliana na grafu zetu? Angalia Kielelezo.

Ufafanuzi: FIND INTERCEPTS YA PARABOLA

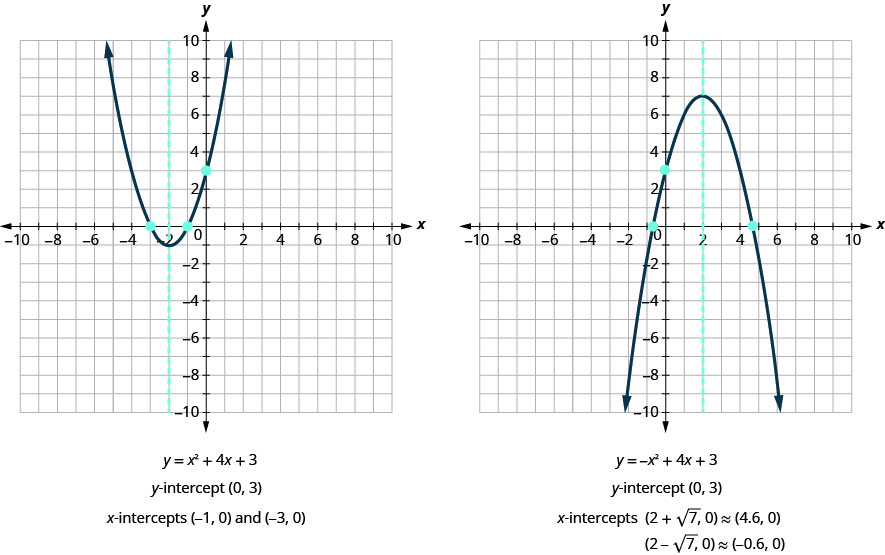
Ili kupata intercepts ya parabola na equation $y=ax^2+bx+c$ :

$\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}$

Mfano $\PageIndex{10}$

Find intercepts ya parabola $y=x^2−2x−8$ .

Jibu

		$.$
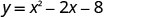
Ili kupata y -intercept, basi x = 0 na kutatua kwa y.		$.$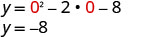
		Wakati x=0, basi y=-8. Y-intercept ni uhakika (0, -8).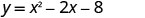
		$.$
Ili kupata x -intercept, basi y = 0 na kutatua kwa x.		$.$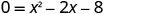
Kutatua kwa factoring.		$.$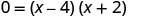
		$.$

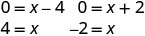
Wakati y=0, basi x=4 au x=-2. Ya x -intercepts ni pointi (4,0) na (-2,0).

Mfano $\PageIndex{11}$

Find intercepts ya parabola $y=x^2+2x−8$ .

Jibu: y: (0, -8); x: (-4,0), (2,0)

Mfano $\PageIndex{12}$

Find intercepts ya parabola $y=x^2−4x−12$ .

Jibu: y: (0, -12); x: (6,0), (-2,0)

Katika sura hii, tumekuwa tunatatua equations quadratic ya fomu $ax^2+bx+c=0$ . Sisi kutatuliwa kwa xx na matokeo yalikuwa ufumbuzi wa equation.

Sasa tunaangalia equations quadratic katika vigezo viwili vya fomu $y=ax^2+bx+c$ . Grafu ya equations hizi ni parabolas. Ya x -intercepts ya parabolas hutokea ambapo y=0.

Kwa mfano:

$\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}$

Ufumbuzi wa equation ya quadratic ni maadili x ya x -intercepts.

Mapema, tuliona kwamba equations quadratic ina 2, 1, au 0 ufumbuzi. Grafu hapa chini zinaonyesha mifano ya parabolas kwa kesi hizi tatu. Kwa kuwa ufumbuzi wa equations hutoa x -intercepts ya grafu, idadi ya x -intercepts ni sawa na idadi ya ufumbuzi.

Hapo awali, tulitumia ubaguzi kuamua idadi ya ufumbuzi wa equation quadratic ya fomu $ax^2+bx+c=0$ . Sasa, tunaweza kutumia ubaguzi kutuambia wangapi x -intercepts kuna kwenye grafu.

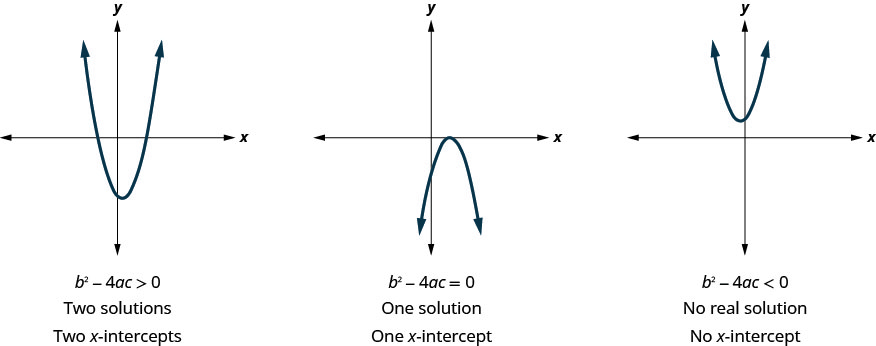
$Takwimu hii inaonyesha grafu tatu kwa upande. Grafu ya kushoto inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Vertex ya parabola iko katika quadrant ya chini ya kulia. Chini ya grafu ni usawa b squared minus 4 c kubwa kuliko 0. Chini hiyo ni taarifa “Ufumbuzi mbili”. Chini ya hayo ni taarifa “Mbili x-intercepts”. Grafu ya kati inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Vertex ya parabola iko kwenye x-axis. Chini ya grafu ni equation b squared minus 4 c sawa 0. Chini hiyo ni taarifa “Suluhisho moja”. Chini ya hiyo ni taarifa “Moja x-intercept”. Grafu ya kulia zaidi inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Vertex ya parabola iko katika quadrant ya juu kushoto. Chini ya grafu ni usawa b squared minus 4 c chini ya 0. Chini hiyo ni taarifa “Hakuna ufumbuzi halisi”. Chini hiyo ni taarifa “Hakuna x-intercept”.$

Kabla ya kuanza kutatua equation quadratic kupata maadili ya x -intercepts, unaweza kutaka kutathmini ubaguzi ili kujua jinsi wengi ufumbuzi kutarajia.

Mfano $\PageIndex{13}$

Find intercepts ya parabola $y=5x^2+x+4$ .

Jibu

		$.$
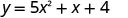
Ili kupata y -intercept, basi x = 0 na kutatua kwa y.	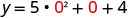	$.$ $.$ Wakati x=0, basi y=4. Y-intercept ni uhakika (0,4).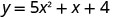
		$.$
Ili kupata x -intercept, basi y = 0 na kutatua kwa x.		$.$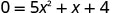
Pata thamani ya wabaguzi kutabiri idadi ya ufumbuzi na hivyo x -intercepts.		b ^ 2,14ac 1^2,1454 1,180 -79
Kwa kuwa thamani ya ubaguzi ni hasi, hakuna ufumbuzi halisi wa equation.		Hakuna x -intercepts.

Mfano $\PageIndex{14}$

Find intercepts ya parabola $y=3x^2+4x+4$ .

Jibu: y: (0,4); x: hakuna

Mfano $\PageIndex{15}$

Find intercepts ya parabola $y=x^2−4x−5$ .

Jibu: y: (0, -5); x: (5,0) (-1,0)

Mfano $\PageIndex{16}$

Find intercepts ya parabola $y=4x^2−12x+9$ .

Jibu

		$.$
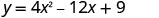
Ili kupata y -intercept, basi x = 0 na kutatua kwa y.		$.$ $.$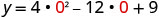
		Wakati x=0, basi y=9. Y-intercept ni uhakika (0,9).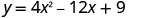
		$.$
Ili kupata x -intercept, basi y = 0 na kutatua kwa x.		$.$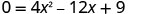
Pata thamani ya wabaguzi kutabiri idadi ya ufumbuzi na hivyo x -intercepts.		b ^ 2,14ac 12^2,1449 144-144 0
		Kwa kuwa thamani ya ubaguzi ni 0, hakuna ufumbuzi halisi wa equation. Kwa hiyo kuna moja x -intercept.
Kutatua equation kwa factoring kamili mraba trinomial.		$.$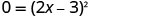
Tumia mali ya Bidhaa ya Zero.		$.$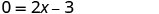
Kutatua kwa x.		$.$ $.$
		Wakati y=0, kisha $\frac{3}{2}$ =x.
		The x -intercept ni uhakika $(\frac{3}{2},0)$ .

Mfano $\PageIndex{17}$

Find intercepts ya parabola $y=−x^2−12x−36.$ .

Jibu: y: (0, -36); x: (-6,0)

Mfano $\PageIndex{18}$

Find intercepts ya parabola $y=9x^2+12x+4$ .

Jibu: y: (0,4); x: $(−\frac{2}{3},0)$

Grafu Ulinganifu wa Quadratic katika Vigezo viwili

Sasa, tuna vipande vyote tunahitaji ili graph equation quadratic katika vigezo mbili. Tunahitaji tu kuwaweka pamoja. Katika mfano unaofuata, tutaona jinsi ya kufanya hivyo.

Jinsi ya Grafu Equation Quadratic katika Vigezo viwili

Mfano $\PageIndex{19}$

Grafu $y=x2−6x+8$ .

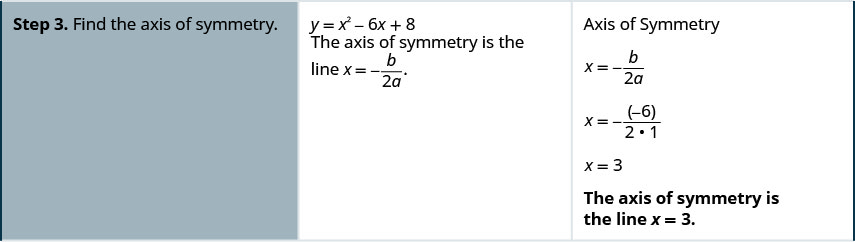
Jibu: $Picha inaonyesha hatua za grafu equation quadratic y sawa x squared minus 6 x plus 8. Hatua ya 1 ni kuandika equation quadratic na y upande mmoja. Equation hii ina y upande mmoja tayari. Thamani ya a ni moja, thamani ya b ni -6 na thamani ya c ni 8.$ $Hatua ya 2 ni kuamua kama parabola inafungua juu au chini. Kwa kuwa ni chanya, parabola inafungua zaidi.$ $Hatua ya 3 ni kupata mhimili wa ulinganifu. mhimili wa ulinganifu ni mstari x sawa hasi b kugawanywa na wingi 2 a kuziba katika maadili ya b na formula inakuwa x sawa hasi -6 kugawanywa na wingi 2 mara 1 ambayo simplifies kwa x sawa 3. Mhimili wa ulinganifu ni mstari x sawa na 3.$ $Hatua ya 4 ni kupata vertex. Vertex iko kwenye mhimili wa ulinganifu. Mbadala x sawa 3 katika equation na kutatua kwa y. equation ni y sawa x squared bala 6 x plus 8. Kubadilisha x na 3 inakuwa y sawa na 3 squared bala mara 6 3 pamoja na 8 ambayo simplifies kwa y sawa -1. Vertex ni (3, -1).$ $Hatua ya 5 ni kupata y-intercept na kupata uhakika ulinganifu kwa y-intercept katika mhimili wa ulinganifu. Sisi badala x sawa 0 katika equation. equation ni y sawa x squared minus 6 x pamoja 8. Kubadilisha x na 0 inakuwa y sawa na 0 squared bala mara 6 0 pamoja 8 ambayo simplifies kwa y sawa 8. Y-intercept ni (0, 8). Tunatumia mhimili wa ulinganifu ili kupata uhakika ulinganifu kwa y-intercept. Y-intercept ni vitengo 3 vya kushoto vya mhimili wa ulinganifu, x sawa na 3. uhakika 3 vitengo na haki ya mhimili wa ulinganifu ina x sawa 6. Hatua ya ulinganifu kwa y-intercept ni (6, 8).$ $Hatua ya 6 ni kupata x-intercepts. Sisi badala y sawa 0 katika equation. equation inakuwa 0 sawa x squared minus 6 x pamoja 8. Tunaweza kutatua equation quadratic kwa factoring kupata 0 sawa na wingi x minus mara 2 kiasi x minus 4. Kutatua kila equation kupata x sawa 2 na x sawa 4. Ya x-intercepts ni (2, 0) na (4, 0).$ $Hatua ya 7 ni grafu parabola. Sisi grafu vertex, intercepts, na uhakika ulinganifu kwa y-intercept. Tunaunganisha pointi hizi tano ili mchoro wa parabola. Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -2 hadi 10. Mhimili wa y wa ndege unatoka -3 hadi 10. Vertex iko kwenye hatua (3, -1). Pointi nne zimepangwa kwenye pembe (0, 8), (6, 8), (2, 0) na (4, 0). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari hupitia kipeo katika x sawa na 3.$

Mfano $\PageIndex{20}$

Graph parabola $y=x^2+2x−8$ .

Jibu: y: (0, -8); x: (2,0), (-4,0);
mhimili: x=-1; vertex: (-1, -9);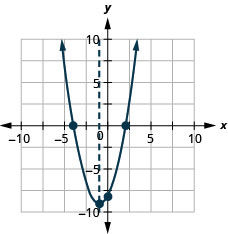
$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -10 hadi 10. Mhimili wa y wa ndege unatoka -10 hadi 10. Vertex iko kwenye hatua (-1, -9). Vipengele vitatu vinapangwa kwenye pembe (0, -8), (2, 0) na (-4, 0). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari unaendelea kupitia vertex saa x sawa -1.$

Mfano $\PageIndex{21}$

Grafu parabola $y=x^2−8x+12$ .

Jibu: y: (0,12); x: (2,0), (6,0);
mhimili: x=4; kipeo :( 4, -4);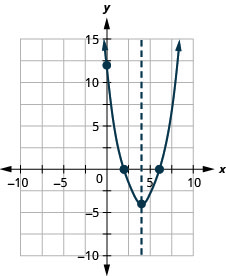
$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -10 hadi 10. Mhimili wa y wa ndege unatoka -10 hadi 10. Vertex iko kwenye hatua (4, -4). Vipengele vitatu vinapangwa kwenye pembe (0, 12), (2, 0) na (6, 0). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. line huenda kwa njia ya kipeo katika x sawa 4.$

Ufafanuzi: GRAPH EQUATION QUADRATIC KATIKA VIGEZO MBILI.

Andika equation quadratic na yy upande mmoja.
Kuamua kama parabola inafungua juu au chini.
Pata mhimili wa ulinganifu.
Pata vertex.
Pata y -intercept. Pata hatua ya ulinganifu kwa y -intercept katika mhimili wa ulinganifu.
Kupata x -intercepts.
Grafu parabola.

Tuliweza kupata x -intercepts katika mfano wa mwisho kwa factoring. Tunapata x -intercepts katika mfano unaofuata kwa kuzingatia, pia.

Mfano $\PageIndex{22}$

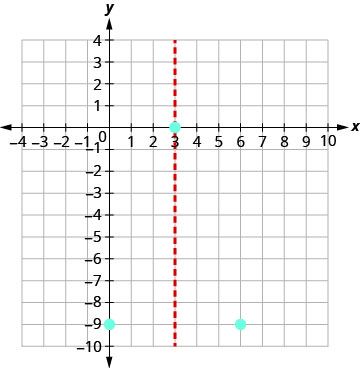
Grafu $y=−x^2+6x−9$ .

Jibu

Equation y ina upande mmoja.		$.$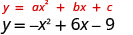
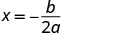
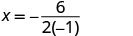
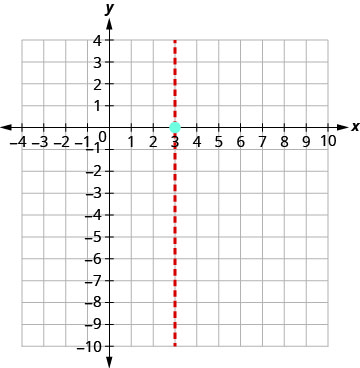
Kwa kuwa ni -1, parabola inafungua chini. Ili kupata mhimili wa ulinganifu, tafuta $x=−\frac{b}{2a}$ .	$.$	$.$ $.$ $.$ Mhimili wa ulinganifu ni x=3. Vertex iko kwenye mstari x=3. $.$
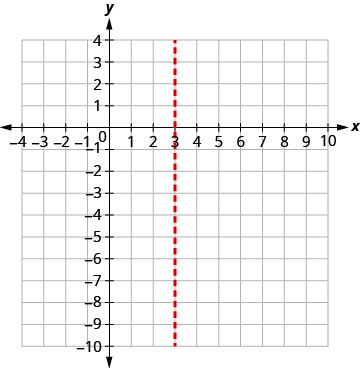
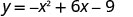
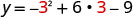
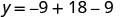
Kupata y wakati x=3.		$.$ $.$ $.$ $.$ Kipeo ni (3,0). $.$
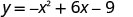
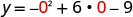
Y-intercept hutokea wakati x=0. Mbadala x=0. Kurahisisha. Hatua (0, -9) ni vitengo vitatu upande wa kushoto wa mstari wa ulinganifu. Hatua ya vitengo vitatu kwa haki ya mstari wa ulinganifu ni (6, -9). Point symmetric kwa y- intercept ni (6, -9)		$.$ $.$ $.$ (0, -9). $.$
Kuzuia x hutokea wakati y=0.		$.$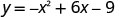
Mbadala y=0.		$.$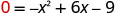
Sababu ya GCF.		$.$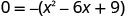
Sababu ya trinomial.		$.$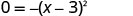
Kutatua kwa x.		$.$
Unganisha pointi kwa graph parabola.		$.$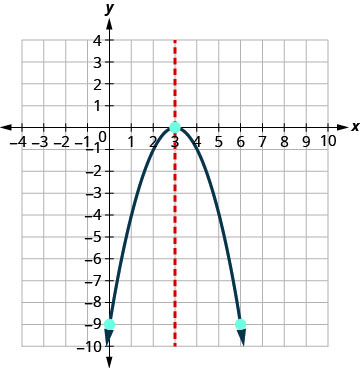

Mfano $\PageIndex{23}$

Grafu parabola $y=−3x^2+12x−12$ .

Jibu

y: (0, -12); x: (2,0);
mhimili: x=2; vertex :( 2,0);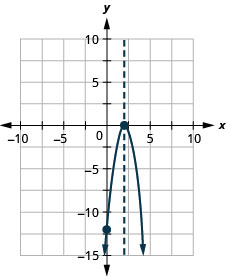

$Grafu inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -10 hadi 10. Mhimili wa y wa ndege unatoka -1 hadi 10. Vertex iko kwenye hatua (2, 0). Hatua nyingine moja ni njama juu ya Curve saa (0, -12). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. line huenda kwa njia ya kipeo katika x sawa 2.$

Mfano $\PageIndex{24}$

Grafu parabola $y=25x^2+10x+1$ .

Jibu

y: (0,1); x: (-15,0);
mhimili: x=-15; kipeo :( -15,0);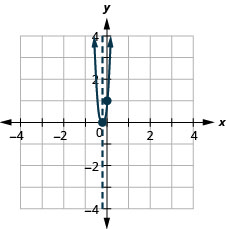

$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -5 hadi 5. Mhimili wa y wa ndege unatoka -5 hadi 10. Vertex iko katika hatua (-1 tano, 0). Moja hatua nyingine ni njama juu ya Curve katika (0, 1). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari unaendelea kupitia vertex saa x sawa -1 tano.$

Kwa grafu ya $y=−x^2+6x−9$ the vertex and the x -intercept walikuwa hatua sawa. Kumbuka jinsi wabaguzi huamua idadi ya ufumbuzi wa equation quadratic? Ubaguzi wa equation $0=−x^2+6x−9$ is 0, so there is only one solution. That means there is only one x -intercept, na ni vertex ya parabola.

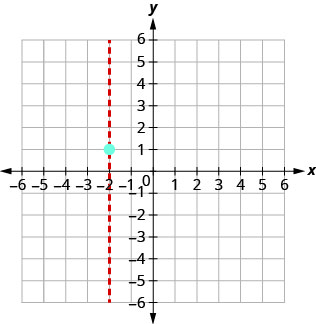
Wangapi x -intercepts ungependa kutarajia kuona kwenye grafu ya $y=x^2+4x+5$ ?

Mfano $\PageIndex{25}$

Grafu $y=x^2+4x+5$ .

Jibu

Equation ina y upande mmoja.		$.$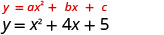
Kwa kuwa ni 1, parabola inafungua zaidi.		$.$
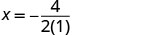
$x=−\frac{b}{2a}$ .		$.$ $.$ $.$ x=π-2. $.$
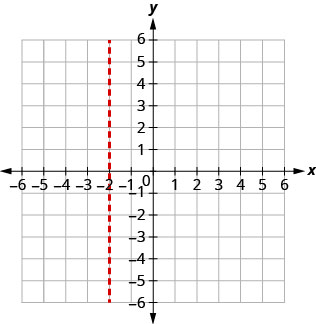
Kipeo kiko kwenye mstari x=-1 2.
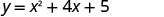
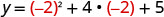
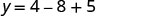
Pata y wakati x=-2.		$.$ $.$ $.$ $.$ (-2,1). $.$
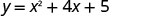
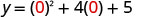
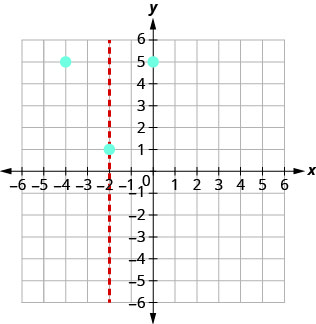
Y-intercept hutokea wakati x=0. Mbadala x=0. Kurahisisha. Hatua (0,5) ni vitengo viwili kwa haki ya mstari wa ulinganifu. Hatua ya vitengo viwili upande wa kushoto wa mstari wa ulinganifu ni (-4,5).		$.$ $.$ $.$ (0,5). $.$ (-4,5)
Kipindi cha x - kinachotokea wakati y=0.
Mbadala y=0. Mtihani ubaguzi.		$.$ $.$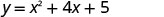
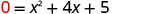
		$b^2−4ac$ $42−4⋅15$ $16−20$ $−4$
Kwa kuwa thamani ya wabaguzi ni hasi, hakuna suluhisho na hivyo hakuna x- intercept. Unganisha pointi kwa graph parabola. Unaweza kutaka kuchagua pointi mbili zaidi kwa usahihi zaidi.		$.$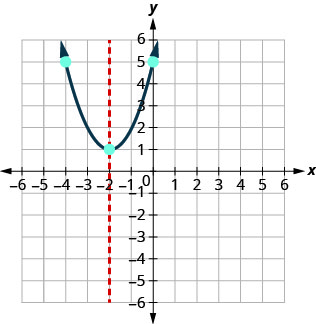

Mfano $\PageIndex{26}$

Grafu parabola $y=2x^2−6x+5$ .

Jibu

y: (0,5); x:hakuna;
mhimili: $x=\frac{3}{2}$ ; vertex: $(\frac{3}{2},\frac{1}{2})$ ;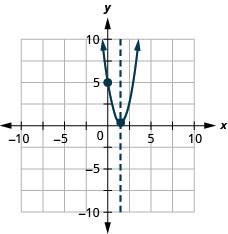

$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -5 hadi 5. Mhimili wa y wa ndege unatoka -5 hadi 10. Vertex iko kwenye hatua (3 halves, nusu 1). Moja hatua nyingine ni njama juu ya Curve katika (0, 5). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari unaendelea kupitia vertex saa x sawa na nusu 3.$

Mfano $\PageIndex{27}$

Grafu parabola $y=−2x^2−1$ .

Jibu

y: (0, -1); x: hakuna;
mhimili: x=0; kipeo :( 0, -1);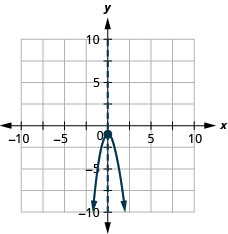

$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -10 hadi 10. Mhimili wa y wa ndege unatoka -10 hadi 10. Vertex iko kwenye hatua (0, -1). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari hupitia kipeo katika x sawa na 0.$

Kutafuta y -intercept kwa kubadilisha x = 0 katika equation ni rahisi, sivyo? Lakini tulihitaji kutumia Mfumo wa Quadratic ili kupata x -intercepts katika Mfano. Tutatumia Mfumo wa Quadratic tena katika mfano unaofuata.

Mfano $\PageIndex{28}$

Grafu $y=2x^2−4x−3$ .

Jibu

$.$

Equation y ina upande mmoja.
Kwa kuwa ni 2, parabola inafungua zaidi.

$.$

Ili kupata mhimili wa ulinganifu, tafuta

$x=−\frac{b}{2a}$

$.$
$.$
$.$
Kipeo ni x=1

Vertex kwenye mstari x=1.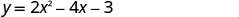

$.$

Pata y wakati x=1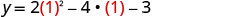

$.$
$.$
$.$
(1, -5)

Y-intercept hutokea wakati x=0.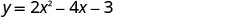

$.$

Mbadala x=0.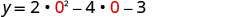

$.$

Kurahisisha.

$.$
Kuzuia y- ni (0, -3)

Hatua (0, -3) ni kitengo kimoja upande wa kushoto wa mstari wa ulinganifu.
Hatua moja kitengo kwa haki ya mstari wa ulinganifu ni (2, -3)

Hatua ya ulinganifu kwa y- intercept ni (2, -3).

Kuzuia x hutokea wakati y=0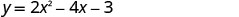

$.$

Mbadala y=0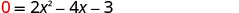

$.$

Tumia Mfumo wa Quadratic.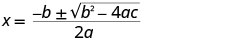

$.$

Mbadala katika maadili ya a, b, c.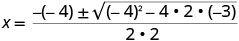

$.$

Kurahisisha.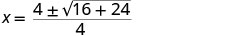

$.$

Kurahisisha ndani ya radical.

$.$

Kurahisisha radical.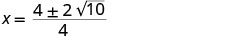

$.$

Sababu ya GCF.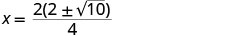

$.$

Ondoa mambo ya kawaida.

$.$

Andika kama equations mbili.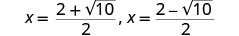

$.$

Takriban maadili.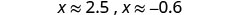

$.$

Maadili ya takriban ya x- intercepts ni (2.5,0) na (-0.6,0).

Grafu parabola kwa kutumia pointi zilizopatikana.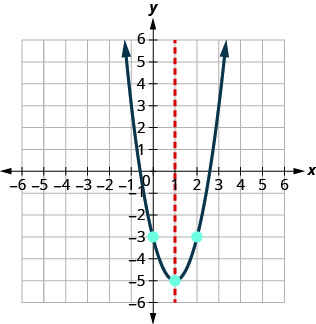

$.$

Mfano $\PageIndex{29}$

Grafu parabola $y=5x^2+10x+3$ .

Jibu

y: (0,3); x: (-1.6,0), (-0.4,0);
mhimili: x = -1; kipeo :( -1, -2);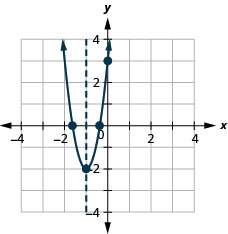

$Grafu inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -5 hadi 5. Mhimili wa y wa ndege unatoka -5 hadi 5. Vertex iko kwenye hatua (-1, -2). Vipengele vingine vitatu vinapangwa kwenye pembe (0, 3), (-1.6, 0), (-0.4, 0). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari unaendelea kupitia vertex saa x sawa -1.$

Mfano $\PageIndex{30}$

Grafu parabola $y=−3x^2−6x+5$ .

Jibu

y: (0,5); x: (0.6,0), (-2.6,0);
mhimili: x = -1; vertex :( -1,8);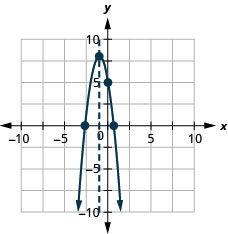

$Grafu inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka -10 hadi 10. Mhimili wa y wa ndege unatoka -10 hadi 10. Vertex iko kwenye hatua (-1, 8). Vipengele vingine vitatu vinapangwa kwenye pembe (0, 5), (0.6, 0) na (-2.6, 0). Pia kwenye grafu ni mstari wa wima uliopigwa unaowakilisha mhimili wa ulinganifu. Mstari unaendelea kupitia vertex saa x sawa -1.$

Tatua Maombi ya kiwango cha juu na cha chini

Kujua kwamba vertex ya parabola ni hatua ya chini au ya juu ya parabola inatupa njia rahisi ya kuamua thamani ya chini au ya juu ya equation quadratic. Kuratibu y ya kipeo ni kiwango cha chini y -thamani ya parabola inayofungua zaidi. Ni upeo y -thamani ya parabola inayofungua chini. Angalia Kielelezo.

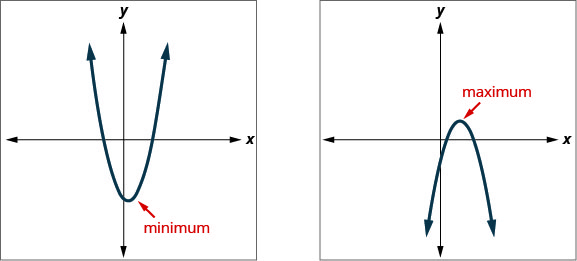
Takwimu hii inaonyesha grafu mbili kwa upande. Grafu ya kushoto inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Vertex ya parabola iko katika quadrant ya juu ya kulia. Vertex inaitwa “kiwango cha juu”. Grafu ya haki inaonyesha parabola ya ufunguzi wa juu iliyopigwa kwenye ndege ya kuratibu x y. Vertex ya parabola iko katika quadrant ya chini ya kulia. Vertex inaitwa “kiwango cha chini”.

Ufafanuzi: MAADILI YA CHINI AU MAXIMUM YA equation quadratic

Kuratibu y ya vertex ya grafu ya equation quadratic ni

thamani ya chini ya equation quadratic kama parabola kufungua zaidi.
upeo thamani ya equation quadratic kama parabola kufungua chini.

Mfano $\PageIndex{31}$

Pata thamani ya chini ya equation ya quadratic $y=x^2+2x−8$ .

Jibu

		$.$
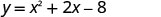
Kwa kuwa ni chanya, parabola inafungua zaidi.
Equation quadratic ina kiwango cha chini.
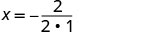
Pata mhimili wa ulinganifu.		$.$ $.$ $.$ x=-1
Kipeo kiko kwenye mstari x=-1.		$.$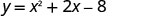
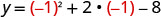
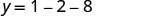
Pata y wakati x=-1.		$.$ $.$ $.$ (-1, -9)
Kwa kuwa parabola ina kiwango cha chini, y- kuratibu ya vertex ni kiwango cha chini y- thamani ya equation quadratic.
Thamani ya chini ya quadratic ni -9 na inatokea wakati x=-1.
Onyesha grafu ili kuthibitisha matokeo.		$.$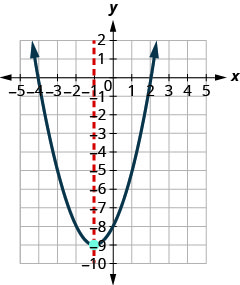

Mfano $\PageIndex{32}$

Pata thamani ya juu au ya chini ya equation ya quadratic $y=x^2−8x+12$ .

Jibu: Thamani ya chini ni -4 wakati x=4.

Mfano $\PageIndex{33}$

Pata thamani ya juu au ya chini ya equation ya quadratic $y=−4x^2+16x−11$ .

Jibu: Thamani ya juu ni 5 wakati x=2.

Tumetumia formula

$\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}$

kuhesabu urefu kwa miguu, h, ya kitu kilichopigwa juu ndani ya hewa na kasi ya awali, $v_{0}$ , baada ya sekunde t.

Fomu hii ni equation quadratic katika tt variable, hivyo grafu yake ni parabola. Kwa kutatua kwa kuratibu za vertex, tunaweza kupata muda gani itachukua kitu kufikia urefu wake wa juu. Kisha, tunaweza kuhesabu urefu wa juu.

Mfano $\PageIndex{34}$

Equation quadratic $h=−16t^2+v_{0}t+h_{0}$ mfano urefu wa volleyball hit moja kwa moja juu na kasi 176 futi kwa sekunde kutoka urefu wa futi 4.

Je! Itachukua sekunde ngapi ya volleyball kufikia urefu wake wa juu?
Pata urefu wa juu wa volleyball.

Jibu

$h=−16t^2+176t+4$

Kwa kuwa ni hasi, parabola inafungua chini.

Equation ya quadratic ina kiwango cha juu.

1.
$\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}$

Kupata h wakati t=5.5.		$.$ $.$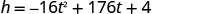
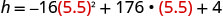
Tumia calculator ili kurahisisha.		$.$
		Kipeo ni (5.5,488)
Kwa kuwa parabola ina kiwango cha juu, h- kuratibu ya vertex ni upeo y -thamani ya equation quadratic.		Thamani ya juu ya quadratic ni futi 488 na hutokea wakati t=sekunde 5.5.

Mfano $\PageIndex{35}$

Equation quadratic $h=−16t^2+128t+32$ hutumiwa kupata urefu wa jiwe kutupwa juu kutoka kimo cha futi 32 kwa kiwango cha 128 ft/sec. Itachukua muda gani kwa jiwe kufikia urefu wake wa juu? Urefu wa juu ni nini? Majibu ya pande zote kwa kumi ya karibu.

Jibu: Itachukua sekunde 4 kufikia urefu wa juu wa miguu 288.

Mfano $\PageIndex{36}$

roketi toy risasi zaidi kutoka ardhini kwa kiwango cha 208 ft/sec ina equation quadratic ya $h=−16t^2+208t$ . Je, roketi itafikia lini urefu wake wa juu? Je! Urefu wa juu utakuwa nini? Majibu ya pande zote kwa kumi ya karibu.

Jibu: Itachukua sekunde 6.5 kufikia urefu wa juu wa futi 676.

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na ufanyie mazoezi ya usawa wa quadratic:

Graphing Quadratic Kazi
Je! Unawezaje kuchora kazi ya quadratic?
Graphing Quadratic Equations

Dhana muhimu

Grafu ya kila equation quadratic ni parabola.
Parabola Mwelekeo Kwa equation quadratic $y=ax^2+bx+c$ , kama
- a> 0, parabola kufungua zaidi.
- a<0, parabola inafungua chini.
Mhimili wa Ulinganifu na Vertex ya Parabola Kwa parabola na equation $y=ax^2+bx+c$ :
- Mhimili wa ulinganifu wa parabola ni mstari $x=−\frac{b}{2a}$ .
- Vertex iko kwenye mhimili wa ulinganifu, hivyo x -kuratibu yake ni $−\frac{b}{2a}$ .
- Ili kupata y -kuratibu ya vertex sisi badala $x=−\frac{b}{2a}$ katika equation quadratic.
Find Intercepts ya Parabola Kupata intercepts ya parabola na equation $y=ax^2+bx+c$ :
$\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}$
Kwa Grafu Equation Quadratic katika Vigezo viwili
1. Andika equation quadratic na yy upande mmoja.
2. Kuamua kama parabola inafungua juu au chini.
3. Pata mhimili wa ulinganifu.
4. Pata vertex.
5. Pata y -intercept. Pata hatua ya ulinganifu kwa y -intercept katika mhimili wa ulinganifu.
6. Kupata x -intercepts.
7. Grafu parabola.
Kiwango cha chini au Maadili ya Upeo wa Quadratic
- Kuratibu y - ya vertex ya grafu ya equation quadratic ni
- thamani ya chini ya equation quadratic kama parabola kufungua zaidi.
- upeo thamani ya equation quadratic kama parabola kufungua chini.

faharasa

mhimili wa ulinganifu: Mhimili wa ulinganifu ni mstari wa wima unaopita katikati ya parabola $y=ax^2+bx+c$ .

parabola: Grafu ya equation quadratic katika vigezo viwili ni parabola.

equation quadratic katika vigezo viwili: Equation quadratic katika vigezo mbili, ambapo a, b, na c ni namba halisi na $a \ge 0$ ni equation ya fomu $y=ax^2+bx+c$ .

vertex: Nambari juu ya parabola iliyo kwenye mhimili wa ulinganifu inaitwa kipeo cha parabola; ni hatua ya chini au ya juu juu juu ya parabola, kulingana na iwapo parabola inafungua juu au chini.

x -intercepts ya parabola: x -intercepts ni pointi juu ya parabola ambapo $y=0$ .

y -intercept ya parabola: y -intercept ni uhakika juu ya parabola ambapo $x=0$ .

Malengo ya kujifunza

Kuwa tayari

Tambua Grafu ya Equation ya Quadratic katika Vigezo viwili

ufafanuzi: QUADRATIC EQUATION KATIKA VIGEZO MBILI

Mfano10.5.1\PageIndex{1}

Mfano10.5.2\PageIndex{2}

Mfano10.5.3\PageIndex{3}

Ufafanuzi: PARABOLA ORIEN

Mfano10.5.4\PageIndex{4}

Mfano10.5.5\PageIndex{5}

Mfano10.5.6\PageIndex{6}

Kupata Axis ya Ulinganifu na Vertex ya Parabola

Ufafanuzi: AXIS YA ULINGANIFU NA VERTEX YA PARABOLA

Mfano10.5.7\PageIndex{7}

Mfano10.5.8\PageIndex{8}

Mfano10.5.9\PageIndex{9}

Kupata Intercepts ya Parabola

Ufafanuzi: FIND INTERCEPTS YA PARABOLA

Mfano10.5.10\PageIndex{10}

Mfano10.5.11\PageIndex{11}

Mfano10.5.12\PageIndex{12}

Mfano10.5.13\PageIndex{13}

Mfano10.5.14\PageIndex{14}

Mfano10.5.15\PageIndex{15}

Mfano10.5.16\PageIndex{16}

Mfano10.5.17\PageIndex{17}

Mfano10.5.18\PageIndex{18}

Grafu Ulinganifu wa Quadratic katika Vigezo viwili

Mfano10.5.19\PageIndex{19}

Mfano10.5.20\PageIndex{20}

Mfano10.5.21\PageIndex{21}

Ufafanuzi: GRAPH EQUATION QUADRATIC KATIKA VIGEZO MBILI.

Mfano10.5.22\PageIndex{22}

Mfano10.5.23\PageIndex{23}

Mfano10.5.24\PageIndex{24}

Mfano10.5.25\PageIndex{25}

Mfano10.5.26\PageIndex{26}

Mfano10.5.27\PageIndex{27}

Mfano10.5.28\PageIndex{28}

Mfano10.5.29\PageIndex{29}

Mfano10.5.30\PageIndex{30}

Tatua Maombi ya kiwango cha juu na cha chini

Ufafanuzi: MAADILI YA CHINI AU MAXIMUM YA equation quadratic

Mfano10.5.31\PageIndex{31}

Mfano10.5.32\PageIndex{32}

Mfano10.5.33\PageIndex{33}

Mfano10.5.34\PageIndex{34}

Mfano10.5.35\PageIndex{35}

Mfano10.5.36\PageIndex{36}

Dhana muhimu

faharasa

Mfano $\PageIndex{1}$

Mfano $\PageIndex{2}$

Mfano $\PageIndex{3}$

Mfano $\PageIndex{4}$

Mfano $\PageIndex{5}$

Mfano $\PageIndex{6}$

Mfano $\PageIndex{7}$

Mfano $\PageIndex{8}$

Mfano $\PageIndex{9}$

Mfano $\PageIndex{10}$

Mfano $\PageIndex{11}$

Mfano $\PageIndex{12}$

Mfano $\PageIndex{13}$

Mfano $\PageIndex{14}$

Mfano $\PageIndex{15}$

Mfano $\PageIndex{16}$

Mfano $\PageIndex{17}$

Mfano $\PageIndex{18}$

Mfano $\PageIndex{19}$

Mfano $\PageIndex{20}$

Mfano $\PageIndex{21}$

Mfano $\PageIndex{22}$

Mfano $\PageIndex{23}$

Mfano $\PageIndex{24}$

Mfano $\PageIndex{25}$

Mfano $\PageIndex{26}$

Mfano $\PageIndex{27}$

Mfano $\PageIndex{28}$

Mfano $\PageIndex{29}$

Mfano $\PageIndex{30}$

Mfano $\PageIndex{31}$

Mfano $\PageIndex{32}$

Mfano $\PageIndex{33}$

Mfano $\PageIndex{34}$

Mfano $\PageIndex{35}$

Mfano $\PageIndex{36}$