9.7: Mizizi ya Juu

Last updated

Nov 1, 2022
Page ID
177421
Save as PDF
- 9.6E: Mazoezi
- 9.7E: Mazoezi

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Punguza maneno na mizizi ya juu
Tumia Mali ya Bidhaa ili kurahisisha maneno na mizizi ya juu
Tumia Mali ya Quotient ili kurahisisha maneno na mizizi ya juu
Ongeza na uondoe mizizi ya juu

Kumbuka

Kurahisisha: $y^{5}y^{4}$ .
Ikiwa umekosa tatizo hili, tathmini Mfano 6.2.7.
Kurahisisha: $(n^2)^6$ .
Kama amekosa tatizo hili, mapitio Mfano 6.2.19.
Kurahisisha: $\frac{x^8}{x^3}$ .
Ikiwa umekosa tatizo hili, kagua Mfano 6.5.1.

Rahisisha Maneno na Mizizi ya Juu

Hadi sasa, katika sura hii tumefanya kazi na mraba na mizizi ya mraba. Sasa tutaongeza kazi yetu ili kujumuisha mamlaka ya juu na mizizi ya juu.

Hebu tuchunguze msamiati fulani kwanza.

$\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}$

Neno 'squared' na 'cubed' linatokana na formula kwa eneo la mraba na kiasi cha mchemraba.

Itakuwa na manufaa kuwa na meza ya nguvu za integers kutoka -5to5. Angalia Kielelezo $\PageIdnex{1}$ .

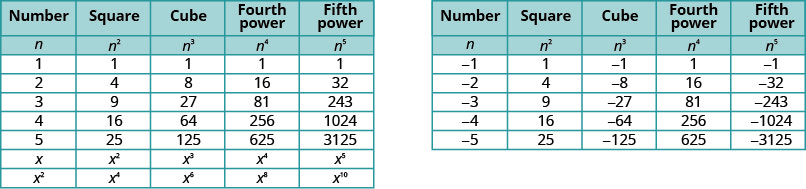
Takwimu hii ina meza mbili. Jedwali la kwanza linaonyesha matokeo ya kuongeza namba 1, 2, 3, 4, 5, x, na x mraba kwa nguvu ya pili, ya tatu, ya nne, na ya tano. Jedwali la pili linaonyesha matokeo ya kuongeza namba hasi moja kwa njia ya tano hasi hadi nguvu ya pili, ya tatu, ya nne, na ya tano. Jedwali la kwanza lina nguzo tano na safu tisa. Ya pili ina nguzo tano na safu saba. Nguzo katika meza zote mbili zimeandikwa, “Nambari,” “Square”, “Cube”, “Nguvu ya Nne,” “Nguvu ya Tano,” hakuna kitu, “Nambari,” “Mraba,” “Cube”, “Nguvu ya Nne,” na “Nguvu ya Tano.” Katika meza zote mbili, mstari unaofuata unasoma: n, n mraba, n cubed, n kwa nguvu ya nne, n kwa nguvu ya tano, hakuna, n, n mraba, n cubed, n kwa nguvu ya nne, na n kwa nguvu ya tano. Katika meza ya kwanza, 1 mraba, 1 cubed, 1 hadi nguvu ya nne, na 1 hadi nguvu ya tano zote zinaonyeshwa kuwa 1. Katika mstari uliofuata, 2 mraba ni 4, 2 cubed ni 8, 2 hadi nguvu ya nne ni 16, na 2 hadi nguvu ya tano ni 32. Katika mstari uliofuata, mraba 3 ni 9, 3 cubed ni 27, 3 hadi nguvu ya nne ni 81, na 3 hadi nguvu ya tano ni 243. Katika mstari uliofuata, mraba 4 ni 16, 4 cubed ni 64, 4 hadi nguvu ya nne ni 246, na 4 hadi nguvu ya tano ni 1024. Katika mstari uliofuata, mraba 5 ni 25, 5 cubed ni 125, 5 hadi nguvu ya nne ni 625, na 5 hadi nguvu ya tano ni 3125. Katika mstari uliofuata, x mraba, x cubed, x kwa nguvu ya nne, na x hadi nguvu ya tano zimeorodheshwa. Katika mstari unaofuata, x mraba mraba ni x kwa nguvu ya nne, x cubed mraba ni x kwa nguvu ya tano, x mraba kwa nguvu ya nne ni x kwa nguvu ya nane, na x mraba kwa nguvu ya tano ni x kwa nguvu ya kumi. Katika meza ya pili, hasi 1 mraba ni 1, hasi 1 cubed ni hasi 1, hasi 1 hadi nguvu ya nne ni 1, na hasi 1 hadi nguvu ya tano ni hasi 1. Katika mstari unaofuata, hasi 2 mraba ni 4, hasi 2 cubed ni hasi 8, hasi 2 hadi nguvu ya nne ni 16, na hasi 2 hadi nguvu ya tano ni hasi 32. Katika mstari unaofuata, hasi 4 mraba ni 16, hasi 4 cubed ni hasi 64, hasi 4 hadi nguvu ya nne ni 256, na hasi 4 hadi nguvu ya tano ni hasi 1024. Katika mstari uliofuata, hasi 5 mraba ni 25, hasi 5 cubed ni hasi 125, hasi 5 hadi nguvu ya nne ni 625, na hasi 5 hadi nguvu ya tano ni hasi 3125. — Kielelezo $\PageIndex{1}$ : Kwanza kupitia nguvu ya tano ya integers kutoka -5 hadi 5.

Angalia ishara katika Kielelezo $\PageIndex{1}$ . Nguvu zote za idadi nzuri ni chanya, bila shaka. Lakini wakati tuna idadi hasi, hata nguvu ni chanya na nguvu isiyo ya kawaida ni hasi. Tutakapiga mstari kwa nguvu za -1 hapa chini ili kukusaidia kuona hili.

$Takwimu hii ina nguzo tano na safu mbili. Mstari wa kwanza huandika kila safu: n, n mraba, n cubed, n kwa nguvu ya nne, na n kwa nguvu ya tano. Mstari wa pili unasoma: hasi 2, 4, hasi 8, 16, na hasi 32.$

Mapema katika sura hii tulifafanua mizizi ya mraba ya namba.

Ikiwa $n^2=m$ , basi n ni mizizi ya mraba ya m.

Na tumetumia nukuu $\sqrt{m}$ kuashiria mizizi kuu ya mraba. Hivyo $\sqrt{m} \ge 0$ daima.

Sasa tutapanua ufafanuzi kwa mizizi ya juu.

Ufafanuzi: N TH ROOT YA NUMBER

Ikiwa $b^n=a$ , basi b ni mtu kwenye mizizi ya namba a.

Mkuu juu ya mizizi ya a imeandikwa $\sqrt[n]{a}=b$

n inaitwa index ya radical.

Hatuandiki index kwa mizizi ya mraba. Tu kama sisi kutumia neno 'cubed' kwa $b^3$ , sisi kutumia neno 'mchemraba mzizi' kwa ajili ya $\sqrt[3]{a}$ .

Sisi rejea Kielelezo $\PageIndex{1}$ kutusaidia kupata mizizi ya juu.

$\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}$

Je, tunaweza kuwa na mizizi hata ya idadi hasi? Hapana. Tunajua kwamba mizizi ya mraba ya namba hasi sio namba halisi. Vile vile ni kweli kwa mizizi yoyote hata. Hata mizizi ya idadi hasi si namba halisi. Mizizi isiyo ya kawaida ya idadi hasi ni namba halisi.

Ufafanuzi: PROPERTIES YA $\sqrt[n]{a}$

Wakati n ni hata idadi na

$a\ge 0$ , basi $\sqrt[n]{a}$ ni idadi halisi
$a < 0$ , basi $\sqrt[n]{a}$ si idadi halisi

Wakati n ni idadi isiyo ya kawaida, $\sqrt[n]{a}$ ni idadi halisi kwa maadili yote ya.

Mfano $\PageIndex{1}$

Kurahisisha:

$\sqrt[3]{8}$
$\sqrt[4]{81}$
$\sqrt[5]{32}$ .

Jibu

1.	$\sqrt[3]{8}$
Tangu $(2)^3=8$ .	2
2.	$\sqrt[4]{81}$
Tangu $(3)^4=81$ .	3
3.	$\sqrt[5]{32}$
Tangu $(2)^5=32$ .	2

Mfano $\PageIndex{2}$

Kurahisisha:

$\sqrt[3]{27}$
$\sqrt[4]{256}$
$\sqrt[5]{243}$ .

Jibu

Mfano $\PageIndex{3}$

Kurahisisha:

$\sqrt[3]{1000}$
$\sqrt[4]{16}$
$\sqrt[5]{32}$ .

Jibu

Mfano $\PageIndex{4}$

Kurahisisha:

$\sqrt[3]{−64}$
$\sqrt[4]{−16}$
$\sqrt[5]{−243}$ .

Jibu

1.	$\sqrt[3]{−64}$
Tangu $(−4)^3=−64$ .	-4
2.	$\sqrt[4]{−16}$
Fikiria, $(?)^4=−16$ .Hakuna idadi halisi iliyoinuliwa kwa nguvu ya nne ni chanya.	Si idadi halisi.
3.	$\sqrt[5]{−243}$
Tangu $(−3)^5=−243$ .	1-3

Mfano $\PageIndex{5}$

Kurahisisha:

$\sqrt[3]{−125}$
$\sqrt[4]{−16}$
$\sqrt[5]{−32}$ .

Jibu

-5
si kweli
-2

Mfano $\PageIndex{6}$

Kurahisisha:

$\sqrt[3]{−216}$
$\sqrt[4]{−81}$
$\sqrt[5]{−1024}$ .

Jibu

-6
si kweli
-4

Tulipofanya kazi na mizizi ya mraba iliyokuwa na vigezo katika radicand, tulizuia vigezo kwa maadili yasiyo ya hasi. Sasa tutaondoa kizuizi hiki.

Mzizi usio wa kawaida wa namba unaweza kuwa chanya au hasi. Tumeona kwamba $\sqrt[3]{−64}=−4$ .

Lakini hata mizizi ya nambari isiyo ya hasi daima sio hasi, kwa sababu tunachukua mkuu katika mizizi.

Tuseme sisi kuanza na =-5.

$\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}$

Tunawezaje kuhakikisha mzizi wa nne wa -5 uliofufuliwa kwa nguvu ya nne, $(−5)^4$ ni 5? Tutaona katika mali zifuatazo.

Ufafanuzi: KURAHISISHA ODD NA EVEN ROOTS

Kwa integer yoyote $n \ge 2$ ,

$\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}$

Ni lazima kutumia thamani kamili ishara wakati sisi kuchukua hata mizizi ya kujieleza na variable katika radical.

Mfano $\PageIndex{7}$

Kurahisisha:

$\sqrt{x^2}$
$\sqrt[3]{n^3}$
$\sqrt[4]{p^4}$
$\sqrt[5]{y^5}$ .

Jibu

Tunatumia thamani kamili ili uhakikishe kupata mizizi nzuri.

1.	$\sqrt{x^2}$
Tangu $(x)^2=x^2$ na tunataka mizizi chanya.	\|x\|
2.	$\sqrt[3]{n^3}$
Tangu $(n)^3=n^3$ . Ni mizizi isiyo ya kawaida kwa hiyo hakuna haja ya ishara ya thamani kamili.	n
3.	$\sqrt[4]{p^4}$
Tangu $(p)^4=p^4$ na tunataka mizizi chanya.	\|p\|
4.	$\sqrt[5]{y^5}$
Tangu $(y)^5=y^5$ . Ni mizizi isiyo ya kawaida kwa hiyo hakuna haja ya ishara ya thamani kamili.	y

Mfano $\PageIndex{8}$

Kurahisisha:

$\sqrt{b^2}$
$\sqrt[3]{w^3}$
$\sqrt[4]{m^4}$
$\sqrt[5]{q^5}$ .

Jibu

Mfano $\PageIndex{9}$

Kurahisisha:

$\sqrt{y^2}$
$\sqrt[3]{p^3}$
$\sqrt[4]{z^4}$
$\sqrt[5]{q^5}$

Jibu

Mfano $\PageIndex{10}$

Kurahisisha:

$\sqrt[3]{y^{18}}$
$\sqrt[4]{z^8}$ .

Jibu

1.	$\sqrt[3]{y^{18}}$
Tangu $(y^6)^3=y^18$ .	$\sqrt[3]{(y^6)^3}$
	$y^6$
2.	$\sqrt[4]{z^8}$
Tangu $(z^2)^4=z^8$ .	$\sqrt[4]{(z^2)^4}$
Kwa kuwa $z^2$ ni chanya, hatuhitaji ishara ya thamani kamili.	$z^2$

Mfano $\PageIndex{11}$

Kurahisisha:

$\sqrt[4]{u^{12}}$
$\sqrt[3]{v^{15}}$ .

Jibu

$u^3$
$v^5$

Mfano $\PageIndex{12}$

Kurahisisha:

$\sqrt[5]{c^{20}}$
$\sqrt[6]{d^{24}}$ .

Jibu

$c^4$
$d^4$

Mfano $\PageIndex{13}$

Kurahisisha:

$\sqrt[3]{64p^6}$
$\sqrt[4]{16q^{12}}$ .

Jibu

1.	$\sqrt[3]{64p^6}$
Andika upya $64p^6$ kama $(4p^2)^3$ .	$\sqrt[3]{(4p^2)^3}$
Chukua mizizi ya mchemraba.	$4p^2$
2.	$\sqrt[4]{16q^{12}}$
Andika upya radicand kama nguvu ya nne.	$\sqrt[4]{(2q^3)^4}$
Chukua mizizi ya nne.	$2\|q^3\|$

Mfano $\PageIndex{14}$

Kurahisisha:

$\sqrt[3]{27x^{27}}$
$\sqrt[4]{81q^{28}}$ .

Jibu

$3x^9$
$3∣q^7∣$

Mfano $\PageIndex{15}$

Kurahisisha:

$\sqrt[3]{125p^9}$
$\sqrt[5]{243q^{25}}$

Jibu

$5p^3$
$3q^5$

Tumia Mali ya Bidhaa ili kurahisisha Maneno na Mizizi ya Juu

Sisi kurahisisha maneno na mizizi ya juu kwa njia sawa sawa na sisi rahisi maneno na mizizi ya mraba. Na juu ya mizizi inachukuliwa kuwa rahisi ikiwa haina sababu za $m^n$ .

Ufafanuzi: KILICHORAHISISHWA KATIKA MI

$\sqrt[n]{a}$ inachukuliwa kilichorahisishwa kama hana sababu za $m^n$ .

Tutazalisha Mali ya Bidhaa ya Mizizi ya Mraba ili kuingiza mizizi yoyote ya integer $n \ge 2$ .

Ufafanuzi: PRODUCT PROPERTY YA N TH ROOTS

$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ na $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$

wakati $\sqrt[n]{a}$ na $\sqrt[n]{b}$ ni namba halisi na kwa integer yoyote $n \ge 2$

Mfano $\PageIndex{16}$

Kurahisisha:

$\sqrt[3]{x^4}$
$\sqrt[4]{x^7}$ .

Jibu

1.	$\sqrt[3]{x^4}$
Andika upya radicna kama bidhaa kwa kutumia sababu kubwa zaidi ya mchemraba.	$\sqrt[3]{x^3·x}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[3]{x^3}·\sqrt[3]{x}$
Kurahisisha.	$x\sqrt[3]{x}$
2.	$\sqrt[4]{x^7}$
Andika upya radicna kama bidhaa kwa kutumia nguvu kubwa zaidi ya nne ya nguvu.	$\sqrt[4]{x^4·x^3}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[4]{x^4}·\sqrt[4]{x^3}$
Kurahisisha.	$\|x\|\sqrt[4]{x^3}$

Mfano $\PageIndex{17}$

Kurahisisha:

$\sqrt[4]{y^6}$
$\sqrt[3]{z^5}$ .

Jibu

$|y∣\sqrt[4]{y^2}$
$z\sqrt[3]{z^2}$

Mfano $\PageIndex{18}$

Kurahisisha:

$\sqrt[5]{p^8}$
$\sqrt[6]{q^{13}}$ .

Jibu

$p\sqrt[5]{p^3}$
$q^2\sqrt[6]{q}$

Mfano $\PageIndex{19}$

Kurahisisha:

$\sqrt[3]{16}$
$\sqrt[4]{243}$ .

Jibu

1.	$\sqrt[3]{16}$
	$\sqrt[3]{2^4}$
Andika upya radicna kama bidhaa kwa kutumia sababu kubwa zaidi ya mchemraba.	$\sqrt[3]{2^3·2}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[3]{2^3}·\sqrt[3]{2}$
Kurahisisha.	$2\sqrt[3]{2}$
2.	$\sqrt[4]{243}$
	$\sqrt[4]{3^5}$
Andika upya radicna kama bidhaa kwa kutumia nguvu kubwa zaidi ya nne ya nguvu.	$\sqrt[4]{3^4·3}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[4]{3^4}·\sqrt[4]{3}$
Kurahisisha.	$3\sqrt[4]{3}$

Mfano $\PageIndex{20}$

Kurahisisha:

$\sqrt[3]{81}$
$\sqrt[4]{64}$ .

Jibu

$3\sqrt[3]{3}$
$2\sqrt[4]{4}$

Mfano $\PageIndex{21}$

Kurahisisha:

$\sqrt[3]{625}$
$\sqrt[4]{729}$ .

Jibu

$5\sqrt[3]{5}$
$3\sqrt[4]{9}$

Usisahau kutumia ishara ya thamani kamili wakati wa kuchukua hata mizizi ya kujieleza na kutofautiana katika radical.

Mfano $\PageIndex{22}$

Kurahisisha:

$\sqrt[3]{24x^7}$
$\sqrt[4]{80y^{14}}$ .

Jibu

1.	$\sqrt[3]{24x^7}$
Andika upya radicand kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\sqrt[3]{2^{3}x^{6}·3x}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}$
Andika upya radicand kwanza kama $(2x^2)^3$	$\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}$
Kurahisisha.	$2x^2\sqrt[3]{3x}$
2.	$\sqrt[4]{80y^{14}}$
Andika upya radicna kama bidhaa kwa kutumia mambo kamili ya nne ya nguvu.	$\sqrt[4]{2^{4}y^{12}·5y^2}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}$
Andika upya radicand kwanza kama $(2y^3)^4$	$\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}$
Kurahisisha.	$2\|y^3\|\sqrt[4]{5y^2}$

Mfano $\PageIndex{23}$

Kurahisisha:

$\sqrt[3]{54p^[10}]$
$\sqrt[4]{64q^{10}}$ .

Jibu

$3p^3\sqrt[3]{2p}$
$2q^2\sqrt[4]{4q^2}$

Mfano $\PageIndex{24}$

Kurahisisha:

$\sqrt[3]{128m^{11}}$
$\sqrt[4]{162n^7}$ .

Jibu

$4m^3\sqrt[3]{2m^2}$
$3|n|\sqrt[4]{2n^3}$

Mfano $\PageIndex{25}$

Kurahisisha:

$\sqrt[3]{−27}$
$\sqrt[4]{−16}$ .

Jibu

1.	$\sqrt[3]{−27}$
Andika upya radicand kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\sqrt[3]{(−3)^3}$
Chukua mizizi ya mchemraba.	1-3
2.	$\sqrt[4]{−16}$
Hakuna idadi halisi n ambapo $n^4=−16$ .	Si idadi halisi.

Mfano $\PageIndex{26}$

Kurahisisha:

$\sqrt[3]{−108}$
$\sqrt[4]{−48}$ .

Jibu

$−3\sqrt[3]{4}$
si kweli

Mfano $\PageIndex{27}$

Kurahisisha:

$\sqrt[3]{−625}$
$\sqrt[4]{−324}$ .

Jibu

$−5\sqrt[3]{5}$
si kweli

Tumia Mali ya Quotient ili kurahisisha Maneno na Mizizi ya Juu

Tunaweza kurahisisha mizizi ya juu na quotients kwa njia ile ile tuliyorahisisha mizizi ya mraba. Kwanza sisi kurahisisha sehemu yoyote ndani ya radical.

Mfano $\PageIndex{28}$

Kurahisisha:

$\sqrt[3]{\frac{a^8}{a^5}}$
$\sqrt[4]{\frac{a^{10}}{a^2}}$ .

Jibu

1.	$\sqrt[3]{\frac{a^8}{a^5}}$
Kurahisisha sehemu chini ya radical kwanza.	$\sqrt[3]{a^3}$
Kurahisisha.	a
2.	$\sqrt[4]{\frac{a^{10}}{a^2}}$
Kurahisisha sehemu chini ya radical kwanza.	$\sqrt[4]{a^8}$
Andika upya radicna kutumia mambo kamili ya nne ya nguvu.	$\sqrt[4]{(a^2)^4}$
Kurahisisha.	$a^2$

Mfano $\PageIndex{29}$

Kurahisisha:

$\sqrt[4]{\frac{x^7}{x^3}}$
$\sqrt[4]{\frac{y^{17}}{y^5}}$ .

Jibu

|x|
$y^3$

Mfano $\PageIndex{30}$

Kurahisisha:

$\sqrt[3]{\frac{m^{13}}{m^7}}$
$\sqrt[5]{\frac{n^{12}}{n^2}}$ .

Jibu

$m^2$
$n^2$

Hapo awali, tulitumia Mali ya Quotient 'katika reverse' ili kurahisisha mizizi ya mraba. Sasa tutazalisha formula ili kuingiza mizizi ya juu.

Ufafanuzi: QUOTIENT PROPERTY YA N THE ROOTS

$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ na $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

lini $\sqrt[n]{a}$ and $\sqrt[n]{b}$ are real numbers, $b \ne 0$ , and for any integer $n \ge 2$

Zoezi $\PageIndex{31}$

Kurahisisha:

$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$

Jibu

1.	$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
Wala radicand ni mchemraba kamilifu, kwa hiyo tumia Mali ya Quotient kuandika kama radical moja.	$\sqrt[3]{\frac{−108}{2}}$
Kurahisisha sehemu chini ya radical.	$\sqrt[3]{−54}$
Andika upya radicand kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\sqrt[3]{(−3)^3·2}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[3]{(−3)^3}·\sqrt[3]{2}$
Kurahisisha.	$−3\sqrt[3]{2}$
2.	$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$
Wala radicand ni nguvu kamili ya nne, hivyo tumia Mali ya Quotient kuandika kama radical moja	$\sqrt[4]{\frac{96x^7}{3x^2}}$
Kurahisisha sehemu chini ya radical.	$\sqrt[4]{32x^5}$
Andika upya radicna kama bidhaa kwa kutumia mambo kamili ya nne ya nguvu.	$\sqrt[4]{2^{4}x^4·2x}$
Andika upya radical kama bidhaa ya radicals mbili.	$\sqrt[4]{(2x)^4}·\sqrt[4]{2x}$
Kurahisisha.	$2\|x\|\sqrt[4]{2x}$

Mfano $\PageIndex{32}$

Kurahisisha:

$\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}$
$\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}$

Jibu

si kweli
$3|m|\sqrt[4]{2m^2}$

Mfano $\PageIndex{33}$

Kurahisisha:

$\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}$
$\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}$ .

Jibu

-4
$3|n|\sqrt[4]{2}$

Ikiwa sehemu ndani ya radical haiwezi kuwa rahisi, tunatumia fomu ya kwanza ya Mali ya Quotient kuandika upya usemi kama quotient ya radicals mbili.

Mfano $\PageIndex{34}$

Kurahisisha:

$\sqrt[3]{\frac{24x^7}{y^3}}$
$\sqrt[4]{\frac{48x^{10}}{y^8}}$ .

Jibu

1.	$\sqrt[3]{\frac{24x^7}{y^3}}$
Sehemu katika radicand haiwezi kuwa rahisi. Tumia Mali ya Quotient kuandika kama radicals mbili.	$\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}$
Andika upya kila radicna kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}$
Andika upya namba kama bidhaa ya radicals mbili.	$\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}$
Kurahisisha.	$\frac{2x^2\sqrt[3]{3x}}{y}$
2.	$\sqrt[4]{\frac{48x^{10}}{y^8}}$
Sehemu katika radicand haiwezi kuwa rahisi. Tumia Mali ya Quotient kuandika kama radicals mbili.	$\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}$
Andika upya kila radicna kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}$
Andika upya namba kama bidhaa ya radicals mbili.	$\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}$
Kurahisisha.	$\frac{2x^2\sqrt[4]{3x^2}}{y^2}$

Mfano $\PageIndex{35}$

Kurahisisha:

$\sqrt[3]{\frac{108c^{10}}{d^6}}$
$\sqrt[4]{\frac{80x^{10}}{y^5}}$ .

Jibu

$\frac{3c^3\sqrt[3]{4c}}{d^2}$
$\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}$

Mfano $\PageIndex{36}$

Kurahisisha:

$\sqrt[3]{\frac{40r^3}{s}}$
$\sqrt[4]{\frac{162m^{14}}{n^{12}}}$

Jibu

$r\sqrt[3]{\frac{40}{s}}$
$\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}$

Ongeza na Ondoa Mizizi ya Juu

Tunaweza kuongeza na kuondoa mizizi ya juu kama tulivyoongeza na kuondokana na mizizi ya mraba. Kwanza tunatoa ufafanuzi rasmi wa radicals kama.

Ufafanuzi: KAMA radicals

Radicals na index sawa na radicand sawa huitwa kama radicals.

Kama radicals wana index sawa na radicand sawa.

$9\sqrt[4]{42x}$ na $−2\sqrt[4]{42x}$ ni kama radicals.
$5\sqrt[3]{125x}$ na $6\sqrt[3]{125y}$ si kama radicals. Radicands ni tofauti.
$2\sqrt[5]{1000q}$ na $−4\sqrt[4]{1000q}$ si kama radicals. Fahirisi ni tofauti.

Sisi kuongeza na Ondoa kama radicals kwa njia ile ile sisi kuongeza na Ondoa kama maneno. Tunaweza kuongeza $9\sqrt[4]{42x}+(−2\sqrt[4]{42x})$ na matokeo ni $7\sqrt[4]{42x}$ .

Mfano $\PageIndex{37}$

Kurahisisha:

$\sqrt[3]{4x}+\sqrt[3]{4x}$
$4\sqrt[4]{8}−2\sqrt[4]{8}$

Jibu

1.	$\sqrt[3]{4x}+\sqrt[3]{4x}$
radicals ni kama, hivyo sisi kuongeza coefficients	$2\sqrt[3]{4x}$
2.	$4\sqrt[4]{8}−2\sqrt[4]{8}$
Radicals ni kama, hivyo sisi Ondoa coefficients.	$2\sqrt[4]{8}$

Mfano $\PageIndex{38}$

Kurahisisha:

$\sqrt[5]{3x}+\sqrt[5]{3x}$
$3\sqrt[3]{9}−\sqrt[3]{9}$

Jibu

$2\sqrt[5]{3x}$
$2\sqrt[3]{9}$

Mfano $\PageIndex{39}$

Kurahisisha:

$\sqrt[4]{10y}+\sqrt[4]{10y}$
$5\sqrt[6]{32}−3\sqrt[6]{32}$ .

Jibu

$2\sqrt[4]{10y}$
$2\sqrt[6]{32}$

Wakati usemi hauonekani kuwa kama radicals, sisi kurahisisha kila radical kwanza. Wakati mwingine hii inasababisha kujieleza na radicals kama.

Mfano $\PageIndex{40}$

Kurahisisha:

$\sqrt[3]{54}−\sqrt[3]{16}$
$\sqrt[4]{48}+\sqrt[4]{243}$ .

Jibu

1.	$\sqrt[3]{54}−\sqrt[3]{16}$
Andika upya kila radicna kutumia mambo kamili ya mchemraba.	$\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}$
Andika upya cubes kamilifu.	$\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}$
Kurahisisha radicals iwezekanavyo.	$3\sqrt[3]{2}−2\sqrt[3]{2}$
Kuchanganya kama radicals.	$\sqrt[3]{2}$
2.	$\sqrt[4]{48}+\sqrt[4]{243}$
Andika upya kwa kutumia mambo kamili ya nne ya nguvu.	$\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}$
Andika upya kila radicna kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}$
Andika upya namba kama bidhaa ya radicals mbili.	$2\sqrt[4]{3}+3\sqrt[4]{3}$
Kurahisisha.	$5\sqrt[4]{3}$

Mfano $\PageIndex{41}$

Kurahisisha:

$\sqrt[3]{192}−\sqrt[3]{81}$
$\sqrt[4]{32}+\sqrt[4]{512}$ .

Jibu

$\sqrt[3]{3}$
$6\sqrt[4]{2}$

Mfano $\PageIndex{42}$

Kurahisisha:

$\sqrt[3]{108}−\sqrt[3]{250}$
$\sqrt[5]{64}+\sqrt[5]{486}$ .

Jibu

$−\sqrt[3]{2}$
$5\sqrt[5]{2}$

Mfano $\PageIndex{43}$

Kurahisisha:

$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
$\sqrt[4]{162y^9}+\sqrt[4]{512y^5}$ .

Jibu

1.	$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
Andika upya kila radicna kutumia mambo kamili ya mchemraba.	$\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}$
Andika upya cubes kamilifu.	$\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}$
Kurahisisha radicals iwezekanavyo.	$2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})$
2.	$\sqrt[4]{162y^9}+\sqrt[4]{516y^5}$
Andika upya kwa kutumia mambo kamili ya nne ya nguvu.	$\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}$
Andika upya kila radicna kama bidhaa kwa kutumia mambo kamili ya mchemraba.	$\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}$
Andika upya namba kama bidhaa ya radicals mbili.	$3y^2\sqrt[4]{2y}+4\|y\|\sqrt[4]{2y}$

Mfano $\PageIndex{44}$

Kurahisisha:

$\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}$
$\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}$ .

Jibu

$2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}$
$3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}$

Mfano $\PageIndex{45}$

Kurahisisha:

$\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}$
$\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}$ .

Jibu

$2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}$
$2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}$

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kurahisisha mizizi ya juu.

Kurahisisha Mizizi ya Juu
Ongeza/Ondoa mizizi na Fahirisi za Juu

Dhana muhimu

Mali ya
$\sqrt[n]{a}$ wakati n ni idadi hata na
- $a \ge 0$ , basi $\sqrt[n]{a}$ ni idadi halisi
- $a < 0$ , basi $\sqrt[n]{a}$ si idadi halisi
- Wakati n ni idadi isiyo ya kawaida, $\sqrt[n]{a}$ ni idadi halisi kwa maadili yote ya.
- Kwa integer yoyote $n \ge 2$ , wakati n ni isiyo ya kawaida $\sqrt[n]{a^n}=a$
- Kwa integer yoyote $n \ge 2$ , wakati n ni hata $\sqrt[n]{a^n}=|a|$
$\sqrt[n]{a}$ inachukuliwa kilichorahisishwa kama hana sababu za $m^n$ .
$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ na $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$
$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ na $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
Ili kuchanganya kama radicals, tu kuongeza au kuondoa coefficients wakati kuweka radical sawa.

faharasa

Katika mizizi ya idadi: Ikiwa $b^n=a$ , basi b ni mtu katika mizizi ya a.

mkuu juu ya mizizi: Mkuu juu ya mizizi ya a imeandikwa $\sqrt[n]{a}$ .

index: $\sqrt[n]{a}$ n inaitwa index ya radical.

kama radicals: Radicals na index sawa na radicand sawa huitwa kama radicals.

Malengo ya kujifunza

Kumbuka

Rahisisha Maneno na Mizizi ya Juu

Ufafanuzi: N TH ROOT YA NUMBER

Ufafanuzi: PROPERTIES YAn√a\sqrt[n]{a}

Mfano9.7.1\PageIndex{1}

Mfano9.7.2\PageIndex{2}

Mfano9.7.3\PageIndex{3}

Mfano9.7.4\PageIndex{4}

Mfano9.7.5\PageIndex{5}

Mfano9.7.6\PageIndex{6}

Ufafanuzi: KURAHISISHA ODD NA EVEN ROOTS

Mfano9.7.7\PageIndex{7}

Mfano9.7.8\PageIndex{8}

Mfano9.7.9\PageIndex{9}

Mfano9.7.10\PageIndex{10}

Mfano9.7.11\PageIndex{11}

Mfano9.7.12\PageIndex{12}

Mfano9.7.13\PageIndex{13}

Mfano9.7.14\PageIndex{14}

Mfano9.7.15\PageIndex{15}

Tumia Mali ya Bidhaa ili kurahisisha Maneno na Mizizi ya Juu

Ufafanuzi: KILICHORAHISISHWA KATIKA MI

Ufafanuzi: PRODUCT PROPERTY YA N TH ROOTS

Mfano9.7.16\PageIndex{16}

Mfano9.7.17\PageIndex{17}

Mfano9.7.18\PageIndex{18}

Mfano9.7.19\PageIndex{19}

Mfano9.7.20\PageIndex{20}

Mfano9.7.21\PageIndex{21}

Mfano9.7.22\PageIndex{22}

Mfano9.7.23\PageIndex{23}

Mfano9.7.24\PageIndex{24}

Mfano9.7.25\PageIndex{25}

Mfano9.7.26\PageIndex{26}

Mfano9.7.27\PageIndex{27}

Tumia Mali ya Quotient ili kurahisisha Maneno na Mizizi ya Juu

Mfano9.7.28\PageIndex{28}

Mfano9.7.29\PageIndex{29}

Mfano9.7.30\PageIndex{30}

Ufafanuzi: QUOTIENT PROPERTY YA N THE ROOTS

Zoezi9.7.31\PageIndex{31}

Mfano9.7.32\PageIndex{32}

Mfano9.7.33\PageIndex{33}

Mfano9.7.34\PageIndex{34}

Mfano9.7.35\PageIndex{35}

Mfano9.7.36\PageIndex{36}

Ongeza na Ondoa Mizizi ya Juu

Ufafanuzi: KAMA radicals

Mfano9.7.37\PageIndex{37}

Mfano9.7.38\PageIndex{38}

Mfano9.7.39\PageIndex{39}

Mfano9.7.40\PageIndex{40}

Mfano9.7.41\PageIndex{41}

Mfano9.7.42\PageIndex{42}

Mfano9.7.43\PageIndex{43}

Mfano9.7.44\PageIndex{44}

Mfano9.7.45\PageIndex{45}

Dhana muhimu

faharasa

Ufafanuzi: PROPERTIES YA $\sqrt[n]{a}$

Mfano $\PageIndex{1}$

Mfano $\PageIndex{2}$

Mfano $\PageIndex{3}$

Mfano $\PageIndex{4}$

Mfano $\PageIndex{5}$

Mfano $\PageIndex{6}$

Mfano $\PageIndex{7}$

Mfano $\PageIndex{8}$

Mfano $\PageIndex{9}$

Mfano $\PageIndex{10}$

Mfano $\PageIndex{11}$

Mfano $\PageIndex{12}$

Mfano $\PageIndex{13}$

Mfano $\PageIndex{14}$

Mfano $\PageIndex{15}$

Mfano $\PageIndex{16}$

Mfano $\PageIndex{17}$

Mfano $\PageIndex{18}$

Mfano $\PageIndex{19}$

Mfano $\PageIndex{20}$

Mfano $\PageIndex{21}$

Mfano $\PageIndex{22}$

Mfano $\PageIndex{23}$

Mfano $\PageIndex{24}$

Mfano $\PageIndex{25}$

Mfano $\PageIndex{26}$

Mfano $\PageIndex{27}$

Mfano $\PageIndex{28}$

Mfano $\PageIndex{29}$

Mfano $\PageIndex{30}$

Zoezi $\PageIndex{31}$

Mfano $\PageIndex{32}$

Mfano $\PageIndex{33}$

Mfano $\PageIndex{34}$

Mfano $\PageIndex{35}$

Mfano $\PageIndex{36}$

Mfano $\PageIndex{37}$

Mfano $\PageIndex{38}$

Mfano $\PageIndex{39}$

Mfano $\PageIndex{40}$

Mfano $\PageIndex{41}$

Mfano $\PageIndex{42}$

Mfano $\PageIndex{43}$

Mfano $\PageIndex{44}$

Mfano $\PageIndex{45}$