9.7E: Mazoezi
- Page ID
- 177438
Mazoezi hufanya kamili
Rahisisha Maneno na Mizizi ya Juu
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[3]{216}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{32}\)
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{243}\)
- Jibu
-
- 3
- 2
- 3
- \(\sqrt[3]{512}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{1}\)
- \(\sqrt[5]{125}\)
- \(\sqrt[4]{1296}\)
- \(\sqrt[5]{1024}\)
- Jibu
-
- 5
- 6
- 4
- \(\sqrt[3]{−8}\)
- \(\sqrt[4]{−81}\)
- \(\sqrt[5]{−32}\)
- \(\sqrt[3]{−64}\)
- \(\sqrt[4]{−16}\)
- \(\sqrt[5]{−243}\)
- Jibu
-
- -4
- si kweli
- 1-3
- \(\sqrt[3]{−125}\)
- \(\sqrt[4]{−1296}\)
- \(\sqrt[5]{−1024}\)
- \(\sqrt[3]{−512}\)
- \(\sqrt[4]{−81}\)
- \(\sqrt[5]{−1}\)
- Jibu
-
- -8
- si idadi halisi
- -1
- \(\sqrt[5]{u^5}\)
- \(\sqrt[8]{v^8}\)
- \(\sqrt[3]{a^3}\)
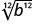
- Jibu
-
- a
- |b|
- \(\sqrt[4]{y^4}\)
- \(\sqrt[7]{m^7}\)
- \(\sqrt[8]{k^8}\)
- \(\sqrt[6]{p^6}\)
- Jibu
-
- |k|
- p
- \(\sqrt[3]{x^9}\)
- \(\sqrt[4]{y^{12}}\)
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- Jibu
-
- \(a^2\)
- \(b^9\)
- \(\sqrt[4]{m^8}\)
- \(\sqrt[5]{n^{20}}\)
- \(\sqrt[6]{r^{12}}\)
- \(\sqrt[3]{s^{30}}\)
- Jibu
-
- \(r^2\)
- \(s^{10}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- \(\sqrt[3]{−8c^9}\)
- \(\sqrt[3]{125d^{15}}\)
- Jibu
-
- \(−2c^3\)
- \(5d^5\)
- \(\sqrt[3]{216a^6}\)
- \(\sqrt[5]{32b^{20}}\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
- Jibu
-
- \(2r^2\)
- \(3s^6\)
Tumia Mali ya Bidhaa ili kurahisisha Maneno na Mizizi ya Juu
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[3]{r^5}\)
- \(\sqrt[4]{s^{10}}\)
- \(\sqrt[5]{u^7}\)
- \(\sqrt[6]{v^{11}}\)
- Jibu
-
- \(u\sqrt[5]{u^2}\)
- \(v\sqrt[6]{v^5}\)
- \(\sqrt[4]{m^5}\)
- \(\sqrt[8]{n^{10}}\)
- \(\sqrt[5]{p^8}\)
- \(\sqrt[3]{q^8}\)
- Jibu
-
- \(p\sqrt[5]{p^3}\)
- \(q^2\sqrt[3]{q^2}\)
- \(\sqrt[4]{32}\)
- \(\sqrt[5]{64}\)
- \(\sqrt[3]{625}\)
- \(\sqrt[6]{128}\)
- Jibu
-
- \(5\sqrt[3]{5}\)
- \(2\sqrt[6]{2}\)
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{256}\)
- \(\sqrt[4]{3125}\)
- \(\sqrt[3]{81}\)
- Jibu
-
- \(5\sqrt[4]{5}\)
- \(3\sqrt[3]{3}\)
- \(\sqrt[3]{108x^5}\)
- \(\sqrt[4]{48y^6}\)
- \(\sqrt[5]{96a^7}\)
- \(\sqrt[3]{375b^4}\)
- Jibu
-
- \(2a\sqrt[5]{3a^2}\)
- \(5b\sqrt[3]{3b}\)
- \(\sqrt[4]{405m^{10}}\)
- \(\sqrt[5]{160n^8}\)
- \(\sqrt[3]{512p^5}\)
- \(\sqrt[4]{324q^7}\)
- Jibu
-
- \(8p\sqrt[3]{p^2}\)
- \(3q\sqrt[4]{4q^3}\)
- \(\sqrt[3]{−864}\)
- \(\sqrt[4]{−256}\)
- \(\sqrt[5]{−486}\)
- \(\sqrt[6]{−64}\)
- Jibu
-
- \(−3\sqrt[5]{2}\)
- si kweli
- \(\sqrt[5]{−32}\)
- \(\sqrt[8]{−1}\)
- \(\sqrt[3]{−8}\)
- \(\sqrt[4]{−16}\)
- Jibu
-
- -2
- si kweli
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[3]{\frac{p^{11}}{p^2}}\)
- \(\sqrt[4]{\frac{q^{17}}{q^{13}}}\)
- \(\sqrt[5]{\frac{d^{12}}{d^7}}\)
- \(\sqrt[8]{\frac{m^{12}}{m^4}}\)
- Jibu
-
- d
- |m|
- \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
- \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
- \(\sqrt[3]{\frac{r^{14}}{r^5}}\)
- \(\sqrt[4]{\frac{c^{21}}{c^9}}\)
- Jibu
-
- \(r^2\)
- \(∣c^3∣\)
- \(\frac{\sqrt[4]{64}}{\sqrt[4]{2}}\)
- \(\frac{\sqrt[5]{128x^8}}{\sqrt[5]{2x^2}}\)
- \(\frac{\sqrt[3]{−625}}{\sqrt[3]{5}}\)
- \(\frac{\sqrt[4]{80m^7}}{\sqrt[4]{5m}}\)
- Jibu
-
- -5
- \(4m\sqrt[4]{m^2}\)
- \(\sqrt[3]{\frac{1050}{2}}\)
- \(\sqrt[4]{\frac{486y^9}{2y^3}}\)
- \(\sqrt[3]{\frac{162}{6}}\)
- \(\sqrt[4]{\frac{160r^{10}}{5r^3}}\)
- Jibu
-
- \(3\sqrt[3]{6}\)
- \(2|r|\sqrt[4]{2r^3}\)
- \(\sqrt[3]{\frac{54a^8}{b^3}}\)
- \(\sqrt[4]{\frac{64c^5}{d^2}}\)
- \(\sqrt[5]{\frac{96r^{11}}{s^{3}}}\)
- \(\sqrt[6]{\frac{128u^7}{v^3}}\)
- Jibu
-
- \(\frac{2r^2\sqrt[5]{3r}}{s^3}\)
- \(\frac{2u\sqrt[6]{2uv^3}}{v}\)
- \(\sqrt[3]{\frac{81s^8}{t^3}}\)
- \(\sqrt[4]{\frac{64p^{15}}{q^{12}}}\)
- \(\sqrt[3]{\frac{625u^{10}}{v^3}}\)
- \(\sqrt[4]{\frac{729c^{21}}{d^8}}\)
- Jibu
-
- \(\frac{5u^3\sqrt[3]{5u}}{v}\)
- \(\frac{3c^5\sqrt[4]{9c}}{d^2}\)
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[7]{8p}+\sqrt[7]{8p}\)
- \(3\sqrt[3]{25}−\sqrt[3]{25}\)
- \(\sqrt[3]{15q}+\sqrt[3]{15q}\)
- \(2\sqrt[4]{27}−6\sqrt[4]{27}\)
- Jibu
-
- \(2\sqrt[3]{15q}\)
- \(−4\sqrt[4]{27}\)
- \(3\sqrt[5]{9x}+7\sqrt[5]{9x}\)
- \(8\sqrt[7]{3q}−2\sqrt[7]{3q}\)
1.
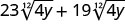
2.
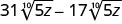
- Jibu
-
1.
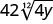
2.
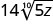
- \(\sqrt[3]{81}−\sqrt[3]{192}\)
- \(\sqrt[4]{512}−\sqrt[4]{32}\)
- \(\sqrt[3]{250}−\sqrt[3]{54}\)
- \(\sqrt[4]{243}−\sqrt[4]{1875}\)
- Jibu
-
- \(5\sqrt[3]{5}−3\sqrt[3]{2}\)
- \(−2\sqrt[4]{3}\)
- \(\sqrt[3]{128}+\sqrt[3]{250}\)
- \(\sqrt[5]{729}+\sqrt[5]{96}\)
- \(\sqrt[4]{243}+\sqrt[4]{1250}\)
- \(\sqrt[3]{2000}+\sqrt[3]{54}\)
- Jibu
-
- \(3\sqrt[4]{3}+5\sqrt[4]{2}\)
- \(13\sqrt[3]{2}\)
- \(\sqrt[3]{64a^{10}}−\sqrt[3]{−216a^{12}}\)
- \(\sqrt[4]{486u^7}+\sqrt[4]{768u^3}\)
- \(\sqrt[3]{80b^5}−\sqrt[3]{−270b^3}\)
- \(\sqrt[4]{160v^{10}}−\sqrt[4]{1280v^3}\)
- Jibu
-
- \(2b\sqrt[3]{10b^2}+3b\sqrt[3]{10}\)
- \(2v^2\sqrt[4]{10v^2}−4\sqrt[4]{5v^3}\)
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt[4]{16}\)
\(\sqrt[6]{64}\)
- Jibu
-
2
\(\sqrt[3]{a^3}\)
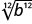
- Jibu
-
|b|
\(\sqrt[3]{−8c^9}\)
\(\sqrt[3]{125d^{15}}\)
- Jibu
-
\(5d^5\)
\(\sqrt[3]{r^5}\)
\(\sqrt[4]{s^{10}}\)
- Jibu
-
\(s^2\sqrt[4]{s^2}\)
\(\sqrt[3]{108x^5}\)
\(\sqrt[4]{48y^6}\)
- Jibu
-
\(2y\sqrt[4]{3y^2}\)
\(\sqrt[5]{−486}\)
\(\sqrt[6]{−64}\)
- Jibu
-
si kweli
\(\frac{\sqrt[4]{64}}{\sqrt[4]{2}}\)
\(\frac{\sqrt[5]{128x^8}}{\sqrt[5]{2x^2}}\)
- Jibu
-
\(2x\sqrt[5]{2x}\)
\(\sqrt[5]{\frac{96r^{11}}{s^3}}\)
\(\sqrt[6]{\frac{128u^7}{v^3}}\)
- Jibu
-
\(\frac{2u^3\sqrt[6]{2uv^3}}{v}\)
\(\sqrt[3]{81}−\sqrt[3]{192}\)
\(\sqrt[4]{512}−\sqrt[4]{32}\)
- Jibu
-
\(4\sqrt[4]{2}\)
\(\sqrt[3]{64a^{10}}−\sqrt[3]{−216a^{12}}\)
\(\sqrt[4]{486u^7}+\sqrt[4]{768u^3}\)
- Jibu
-
\(3u\sqrt[4]{6u^3}+4\sqrt[4]{3u^3}\)
kila siku Math
Ukuaji wa idadi ya watu\(10·x^n\) mifano ya kujieleza ukuaji wa idadi ya watu mold baada ya vizazi n. Kulikuwa na spores 10 mwanzoni, na kila mmoja alikuwa na watoto wa x. Hivyo\(10·x^n\) ni idadi ya watoto katika kizazi cha tano. Katika kizazi cha tano kulikuwa na watoto 10,240. \(\sqrt[5]{\frac{10,240}{10}}\)Kurahisisha maneno ili kuamua idadi ya watoto wa kila spore.
Kuenea kwa virusi Maneno ya\(3·x^n\) kujieleza kuenea kwa virusi baada ya mizunguko n. Kulikuwa na watu watatu awali walioambukizwa na virusi, na kila mmoja wao aliambukizwa x watu. Hivyo\(3·x^4\) ni idadi ya watu walioambukizwa kwenye mzunguko wa nne. Katika mzunguko wa nne watu 1875 waliambukizwa. Kurahisisha usemi\(\sqrt[4]{\frac{1875}{3}}\) ili kuamua idadi ya watu kila mtu aliyeambukizwa.
- Jibu
-
5
Mazoezi ya kuandika
Eleza jinsi unavyojua hilo\(\sqrt[5]{x^{10}}=x^2\).
Eleza\(\sqrt[4]{−64}\) kwa nini si idadi halisi lakini\(\sqrt[3]{−64}\) ni.
- Jibu
-
Majibu yanaweza kutofautiana.
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
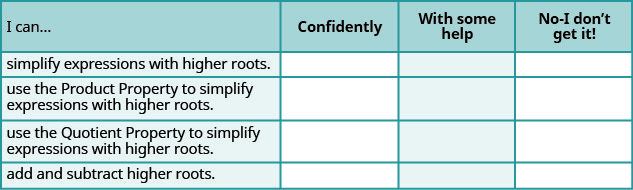
ⓑ Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?


