6.7: Integer Exponents na Nukuu ya kisayansi
- Page ID
- 177782
Mwishoni mwa sehemu hii, utaweza:
- Tumia ufafanuzi wa exponent hasi
- Kurahisisha maneno na exponents integer
- Badilisha kutoka notation decimal kwa notation kisayansi
- Badilisha notation ya kisayansi kwa fomu ya decimal
- Kuzidisha na ugawanye kwa kutumia nukuu
Kabla ya kuanza, fanya jaribio hili la utayari.
- ni thamani ya mahali ya 6 katika idadi 64891 nini?
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.2.1. - Jina la decimal: 0.0012.
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.8.1. - Ondoa: 5- (-3).
Kama amekosa tatizo hili, kupitia Zoezi 1.4.33.
Tumia Ufafanuzi wa Mtazamaji Mbaya
Tuliona kwamba Quotient Mali kwa Exponents ilianzisha mapema katika sura hii, ina aina mbili kulingana na kama exponent ni kubwa katika kadiri au denominator.
Kama ni idadi halisi,\(a\neq0\), na m na n ni idadi nzima, basi
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]
na
\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Nini kama sisi tu Ondoa exponents bila kujali ambayo ni kubwa?
Hebu fikiria\(\dfrac{x^{2}}{x^{5}}\).
Sisi Ondoa exponent katika denominator kutoka exponent katika nambari.
\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]
Tunaweza pia kurahisisha\(\dfrac{x^{2}}{x^{5}}\) kwa kugawa mambo ya kawaida:
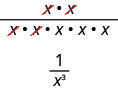
yake ina maana kwamba\(x^{-3}=\dfrac{1}{x^{3}}\) na inatuongoza kwa ufafanuzi wa exponent hasi.
Ikiwa n ni integer na\(a\neq 0\), basi\(a^{-n}=\dfrac{1}{a^{n}}\)
Mtazamaji hasi anatuambia tunaweza kuandika tena maneno kwa kuchukua usawa wa msingi na kisha kubadilisha ishara ya exponent.
Maneno yoyote ambayo ina vielelezo hasi hayakufikiriwa kuwa katika fomu rahisi. Sisi kutumia ufafanuzi wa exponent hasi na mali nyingine ya exponents kuandika kujieleza na exponents chanya tu.
Kwa mfano, ikiwa baada ya kurahisisha kujieleza tunakaribia na maneno\(x^{-3}\), tutachukua hatua moja zaidi na kuandika\(\dfrac{1}{x^{3}}\). Jibu linachukuliwa kuwa katika fomu rahisi wakati ina maonyesho mazuri tu.
Kurahisisha:
- \(4^{-2}\)
- \(10^{-3}\)
- Jibu
-
- \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
- \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)
Kurahisisha:
- \(2^{-3}\)
- \(10^{-7}\)
- Jibu
-
- \(\dfrac{1}{8}\)
- \(\dfrac{1}{10^{7}}\)
Kurahisisha:
- \(3^{-2}\)
- \(10^{-4}\)
- Jibu
-
- \(\dfrac{1}{9}\)
- \(\dfrac{1}{10,000}\)
Katika Zoezi\(\PageIndex{1}\) sisi alimfufua integer kwa exponent hasi. Nini kinatokea wakati sisi kuongeza sehemu kwa exponent hasi? Tutaanza kwa kuangalia nini kinatokea kwa sehemu ambayo nambari ni moja na ambaye denominator ni integer alimfufua kwa exponent hasi.
\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)
Hii inasababisha Mali ya Exponents Hasi.
Ikiwa n ni integer na\(a\neq 0\), basi\(\dfrac{1}{a^{-n}}=a^{n}\).
Kurahisisha:
- \(\dfrac{1}{y^{-4}}\)
- \(\dfrac{1}{3^{-2}}\)
- Jibu
-
- \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
- \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)
Kurahisisha:
- \(\dfrac{1}{p^{-8}}\)
- \(\dfrac{1}{4^{-3}}\)
- Jibu
-
- \(p^{8}\)
- 64
Kurahisisha:
- \(\dfrac{1}{q^{-7}}\)
- \(\dfrac{1}{2^{-4}}\)
- Jibu
-
- \(q^{7}\)
- 16
Tuseme sasa tuna sehemu alimfufua kwa exponent hasi. Hebu kutumia ufafanuzi wetu wa exponents hasi kutuongoza mali mpya.
\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)
Ili kupata kutoka sehemu ya awali alimfufua kwa exponent hasi kwa matokeo ya mwisho, sisi alichukua usawa wa msingi-sehemu - na iliyopita ishara ya exponent.
Hii inatuongoza kwa Quotient kwa Nguvu Nguvu Mali.
Ikiwa\(a\) na\(b\) ni namba halisi,\(a \neq 0, b \neq 0,\) na\(n\) ni integer, basi\(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)
Kurahisisha:
- \(\left(\dfrac{5}{7}\right)^{-2}\)
- \(\left(-\dfrac{2 x}{y}\right)^{-3}\)
- Jibu
-
- \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
- \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)
Kurahisisha:
- \(\left(\dfrac{2}{3}\right)^{-4}\)
- \(\left(-\dfrac{6 m}{n}\right)^{-2}\)
- Jibu
-
- \(\dfrac{81}{16} \)
- \(\dfrac{n^{2}}{36 m^{2}}\)
Kurahisisha:
- \(\left(\dfrac{3}{5}\right)^{-3}\)
- \(\left(-\dfrac{a}{2 b}\right)^{-4}\)
- Jibu
-
- \(\dfrac{125}{27}\)
- \(\dfrac{16 b^{4}}{a^{4}}\)
Wakati kurahisisha kujieleza na exponents, ni lazima kuwa makini kwa usahihi kutambua msingi.
Kurahisisha:
- \((-3)^{-2}\)
- \(-3^{-2}\)
- \(\left(-\dfrac{1}{3}\right)^{-2}\)
- \(-\left(\dfrac{1}{3}\right)^{-2}\)
- Jibu
-
- Hapa exponent inatumika kwa msingi -3. \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
- Maneno\(-3^{-2}\) yanamaanisha “kupata kinyume cha\(3^{-2}\)”. Hapa exponent inatumika kwa msingi 3. \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
- Hapa exponent inatumika kwa msingi\(\left(-\dfrac{1}{3}\right)\). \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
- Maneno\(-\left(\dfrac{1}{3}\right)^{-2}\) yanamaanisha “kupata kinyume cha\(\left(\dfrac{1}{3}\right)^{-2}\)”. Hapa exponent inatumika kwa msingi\(\left(\dfrac{1}{3}\right)\). \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)
Kurahisisha:
- \((-5)^{-2}\)
- \(-5^{-2}\)
- \(\left(-\dfrac{1}{5}\right)^{-2}\)
- \(-\left(\dfrac{1}{5}\right)^{-2}\)
- Jibu
-
- \(\dfrac{1}{25}\)
- \(-\dfrac{1}{25}\)
- 25
- -25
Kurahisisha:
- \((-7)^{-2}\)
- \(-7^{-2}\)
- \(\left(-\dfrac{1}{7}\right)^{-2}\)
- \(-\left(\dfrac{1}{7}\right)^{-2}\)
- Jibu
-
- \(\dfrac{1}{49}\)
- \(-\dfrac{1}{49}\)
- 49
- -49
Lazima tuwe makini kufuata Amri ya Uendeshaji. Katika mfano unaofuata, sehemu (a) na (b) zinaonekana sawa, lakini matokeo ni tofauti.
Kurahisisha:
- 4\(\cdot 2^{-1}\)
- \((4 \cdot 2)^{-1}\)
- Jibu
-
- \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
- \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)
Kurahisisha:
- 6\(\cdot 3^{-1}\)
- \((6 \cdot 3)^{-1}\)
- Jibu
-
- 2
- \(\dfrac{1}{18}\)
Kurahisisha:
- 8\(\cdot 2^{-2}\)
- \((8 \cdot 2)^{-2}\)
- Jibu
-
- 2
- \(\dfrac{1}{256}\)
Wakati variable ni alimfufua kwa exponent hasi, sisi kuomba ufafanuzi njia ile ile tulivyofanya na idadi. Sisi kudhani vigezo vyote ni yasiyo ya sifuri.
Kurahisisha:
- \(x^{-6}\)
- \(\left(u^{4}\right)^{-3}\)
- Jibu
-
- \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
- \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)
Kurahisisha:
- \(y^{-7}\)
- \(\left(z^{3}\right)^{-5}\)
- Jibu
-
- \(\dfrac{1}{y^{7}}\)
- \(\dfrac{1}{z^{15}}\)
Kurahisisha:
- \(p^{-9}\)
- \(\left(q^{4}\right)^{-6}\)
- Jibu
-
- \(\dfrac{1}{p^{9}}\)
- \(\dfrac{1}{q^{24}}\)
Wakati kuna bidhaa na exponent tunapaswa kuwa makini kutumia exponent kwa kiasi sahihi. Kwa mujibu wa Utaratibu wa Uendeshaji, sisi kurahisisha maneno katika mabano kabla ya kutumia exponents. Tutaona jinsi hii inafanya kazi katika mfano unaofuata.
Kurahisisha:
- 5\(y^{-1}\)
- \((5 y)^{-1}\)
- \((-5 y)^{-1}\)
- Jibu
-
- \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
- \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
- \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)
Kurahisisha:
- 8\(p^{-1}\)
- \((8 p)^{-1}\)
- \((-8 p)^{-1}\)
- Jibu
-
- \(\dfrac{8}{p}\)
- \(\dfrac{1}{8 p}\)
- \(-\dfrac{1}{8 p}\)
Kurahisisha:
- 11\(q^{-1}\)
- \((11 q)^{-1}-(11 q)^{-1}\)
- \((-11 q)^{-1}\)
- Jibu
-
- \(\dfrac{11}{1 q}\)
- \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
- \(-\dfrac{1}{11 q}\)
Kwa vielelezo hasi, Utawala wa Quotient unahitaji fomu moja tu\(\dfrac{a^{m}}{a^{n}}=a^{m-n},\) ya\(a \neq 0\) 0. Wakati exponent katika denominator ni kubwa kuliko exponent katika nambari, exponent ya quotient itakuwa hasi.
Kurahisisha Maneno na Exponents Integer
Yote ya mali exponent sisi maendeleo mapema katika sura na idadi nzima exponents kuomba exponents integer, pia. Sisi restate yao hapa kwa ajili ya kumbukumbu.
Kama\(a\) na\(b\) ni idadi halisi,\(m\) na\(n\) ni integers, basi
\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)
Kurahisisha:
- \(x^{-4} \cdot x^{6}\)
- \(y^{-6} \cdot y^{4}\)
- \(z^{-5} \cdot z^{-3}\)
- Jibu
-
- \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
- \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
- \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)
Kurahisisha:
- \(x^{-3} \cdot x^{7}\)
- \(y^{-7} \cdot y^{2}\)
- \(z^{-4} \cdot z^{-5}\)
- Jibu
-
- \(x^{4}\)
- \(\dfrac{1}{y^{5}}\)
- \(\dfrac{1}{z^{9}}\)
Kurahisisha:
- \(a^{-1} \cdot a^{6}\)
- \(b^{-8} \cdot b^{4}\)
- \(c^{-8} \cdot c^{-7}\)
- Jibu
-
- \(a^{5}\)
- \(\dfrac{1}{b^{4}}\)
- \(\dfrac{1}{c^{15}}\)
Katika mifano miwili ijayo, tutaweza kuanza kwa kutumia Mali Commutative kwa kundi vigezo sawa pamoja. Hii inafanya kuwa rahisi kutambua besi kama kabla ya kutumia Mali ya Bidhaa.
Kurahisisha:\(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)
- Jibu
-
\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)
Kurahisisha:\(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)
- Jibu
-
\(\frac{1}{p^3 q^3}\)
Kurahisisha:\(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)
- Jibu
-
\(\frac{1}{r^2 s^8}\)
Ikiwa monomials zina coefficients za namba, tunazidisha coefficients, kama tulivyofanya mapema.
Kurahisisha:\(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)
- Jibu
-
\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)
Kurahisisha:\(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)
- Jibu
-
\(-\frac{12v^5}{u}\)
Kurahisisha:\(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)
- Jibu
-
\(\frac{30d^3}{c^8}\)
Katika mifano miwili ijayo, tutatumia Mali ya Nguvu na Bidhaa kwa Mali ya Nguvu.
Kurahisisha:\(\left(6 k^{3}\right)^{-2}\)
- Jibu
-
\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)
Kurahisisha:\(\left(-4 x^{4}\right)^{-2}\)
- Jibu
-
\(\frac{1}{16x^8}\)
Kurahisisha:\(\left(2 b^{3}\right)^{-4}\)
- Jibu
-
\(\frac{1}{16b^{12}}\)
Kurahisisha:\(\left(5 x^{-3}\right)^{2}\)
- Jibu
-
\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)
Kurahisisha:\(\left(8 a^{-4}\right)^{2}\)
- Jibu
-
\(\frac{64}{a^8}\)
Kurahisisha:\(\left(2 c^{-4}\right)^{3}\)
- Jibu
-
\(\frac{8}{c^{12}}\)
Ili kurahisisha sehemu, sisi kutumia Quotient Mali na Ondoa exponents.
Kurahisisha:\(\dfrac{r^{5}}{r^{-4}}\)
- Jibu
-
\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)
Kurahisisha:\(\dfrac{x^{8}}{x^{-3}}\)
- Jibu
-
\(x^{11}\)
Kurahisisha:\(\dfrac{y^{8}}{y^{-6}}\)
- Jibu
-
\(y^{14}\)
Badilisha kutoka Nukuu ya Decimal hadi Uthibitishaji wa kisayansi
Kumbuka kufanya kazi na thamani ya mahali kwa idadi nzima na decimals? Mfumo wetu wa nambari unategemea nguvu za 10. Tunatumia makumi, mamia, maelfu, na kadhalika. Nambari zetu za decimal pia zinategemea nguvu za kumi na kumi, hundredths, thousandths, na kadhalika. Fikiria idadi 4,000 na 0.004. Tunajua kwamba 4,000 ina maana\(4 \times 1,000\) na 0.004 ina maana\(4 \times \dfrac{1}{1,000}\).
Kama sisi kuandika 1000 kama nguvu ya kumi katika fomu kielelezo, tunaweza kuandika upya namba hizi kwa njia hii:
\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]
Nambari inapoandikwa kama bidhaa ya namba mbili, ambapo sababu ya kwanza ni namba kubwa kuliko au sawa na moja lakini chini ya 10, na sababu ya pili ni nguvu ya 10 iliyoandikwa kwa umbo la kielelezo, inasemekana kuwa katika nukuu ya kisayansi.
Nambari inaelezwa katika nukuu ya kisayansi wakati ni ya fomu
\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]
Ni desturi katika nukuu ya kisayansi kutumia kama ishara ya\(\times\) kuzidisha, ingawa tunaepuka kutumia ishara hii mahali pengine katika algebra.
Kama sisi kuangalia nini kilichotokea kwa uhakika decimal, tunaweza kuona njia ya kubadilisha kwa urahisi kutoka notation decimal kwa notation kisayansi.
Katika matukio hayo yote, decimal ilihamishwa maeneo 3 ili kupata sababu ya kwanza kati ya 1 na 10.
\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)
Andika katika nukuu ya kisayansi: 37000.
- Jibu
-
Andika katika nukuu ya kisayansi: 96000.
- Jibu
-
\(9.6 \times 10^{4}\)
Andika katika nukuu ya kisayansi: 48300.
- Jibu
-
\(4.83 \times 10^{4}\)
- Hatua ya 1. Hoja uhakika decimal ili sababu ya kwanza ni kubwa kuliko au sawa na 1 lakini chini ya 10.
- Hatua ya 2. Hesabu idadi ya maeneo ya decimal, n, kwamba hatua ya decimal ilihamishwa.
- Hatua ya 3. Andika namba kama bidhaa yenye nguvu ya 10.
Ikiwa nambari ya awali ni:- zaidi ya 1, nguvu ya 10 itakuwa 10 n.
- kati ya 0 na 1, nguvu ya 10 itakuwa 10 -n.
- Hatua ya 4. Angalia.
Andika katika nukuu ya kisayansi: 0.0052.
- Jibu
-
Nambari ya awali, 0.0052, ni kati ya 0 na 1 hivyo tutakuwa na nguvu hasi ya 10.
Hoja uhakika decimal kupata 5.2, idadi kati ya 1 na 10. Hesabu idadi ya maeneo ya decimal hatua ilihamishwa. Andika kama bidhaa yenye nguvu ya 10. Angalia. \(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\) 0.0052
Andika katika nukuu ya kisayansi: 0.0078
- Jibu
-
\(7.8 \times 10^{-3}\)
Andika katika nukuu ya kisayansi: 0.0129
- Jibu
-
\(1.29 \times 10^{-2}\)
Badilisha Nukuu ya kisayansi kwa Fomu ya Decima
Tunawezaje kubadilisha kutoka kwa nukuu ya kisayansi hadi fomu ya decimal? Hebu tuangalie namba mbili zilizoandikwa katika nukuu ya kisayansi na uone.
\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]
Ikiwa tunaangalia eneo la uhakika wa decimal, tunaweza kuona njia rahisi ya kubadilisha nambari kutoka kwa nukuu ya kisayansi hadi fomu ya decimal.
\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]
Katika matukio hayo yote hatua ya decimal ilihamia maeneo 4. Wakati exponent alikuwa chanya, decimal wakiongozwa na haki. Wakati kielelezo kilikuwa hasi, hatua ya decimal ilihamia upande wa kushoto.
Badilisha kwenye fomu ya decimal:\(6.2 \times 10^{3}\)
- Jibu
-
Badilisha kwenye fomu ya decimal:\(1.3 \times 10^{3}\)
- Jibu
-
\(1,300\)
Badilisha kwenye fomu ya decimal:\(9.25 \times 10^{4}\)
- Jibu
-
\(92,500\)
Hatua hizi zimefupishwa hapa chini.
Badilisha notation ya kisayansi kwa fomu ya decimal.
Ili kubadilisha notation ya kisayansi kwa fomu ya decimal:
- Hatua ya 1. Kuamua exponent\(n\),, juu ya sababu\(10\).
- Hatua ya 2. Hoja\(n\) maeneo ya decimal, uongeze zero ikiwa inahitajika.
- Kama exponent ni chanya, hoja decimal uhakika\(n\) maeneo ya haki.
- Kama exponent ni hasi, hoja decimal uhakika\(|n|\) maeneo kwa upande wa kushoto.
- Hatua ya 3. Angalia.
Badilisha kwenye fomu ya decimal:\(8.9\times 10^{-2}\)
- Jibu
-
Kuamua exponent\(n\),, juu ya sababu\(10\). Tangu exponent ni hasi, hoja decimal uhakika 2 maeneo upande wa kushoto. Kuongeza zeros kama inahitajika kwa ajili ya placeholders.
Badilisha kwenye fomu ya decimal:\(1.2 \times 10^{-4}\)
- Jibu
-
\(0.00012\)
Badilisha kwenye fomu ya decimal:\(7.5 \times 10^{-2}\)
- Jibu
-
\(0.075\)
Kuzidisha na Gawanya Kutumia Notation ya
Wanaastronomia hutumia idadi kubwa sana kuelezea umbali katika ulimwengu na umri wa nyota na sayari. Wanakemia hutumia namba ndogo sana kuelezea ukubwa wa atomu au chaji kwenye elektroni. Wanasayansi wanapofanya mahesabu kwa idadi kubwa sana au ndogo sana, hutumia notation ya kisayansi. Nukuu ya kisayansi hutoa njia ya mahesabu kufanywa bila kuandika zero nyingi. Tutaona jinsi Mali ya Watazamaji hutumiwa kuzidisha na kugawanya idadi katika nukuu ya kisayansi.
Kuzidisha. Andika majibu katika fomu ya decimal:\(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)
- Jibu
-
\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)
Kuzidisha\((3\times 10^{6})(2\times 10^{-8})\). Andika majibu katika fomu ya decimal.
- Jibu
-
\(0.06\)
Kuzidisha\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\). Andika majibu katika fomu ya decimal.
- Jibu
-
\(0.009\)
Gawanya. Andika majibu katika fomu ya decimal:\(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)
- Jibu
-
\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)
Gawanya\(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\) Andika majibu katika fomu ya decimal.
- Jibu
-
\(400,000\)
Gawanya\(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\) Andika majibu katika fomu ya decimal.
- Jibu
-
\(20,000\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na exponents integer na nukuu kisayansi:
- Watetezi hasi
- Nukuu ya kisayansi
- Nukuu ya kisayansi 2
Dhana muhimu
- Mali ya Watazamaji Hasi
- Ikiwa\(n\) ni integer chanya na\(a \ne 0\), basi\(\dfrac{1}{a^{−n}}=a^n\)
- Ikiwa\(n\) ni integer chanya na\(a \ne 0\), basi\(\dfrac{1}{a^{−n}}=a^n\)
- Quotient kwa Exponent Hasi
- Ikiwa\(a\) na\(b\) ni namba halisi,\(b \ne 0\) na\(n\) ni integer, basi\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Ikiwa\(a\) na\(b\) ni namba halisi,\(b \ne 0\) na\(n\) ni integer, basi\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Ili kubadilisha notation ya kisayansi kwa fomu ya decimal:
- Kuamua exponent,\(n\) kwa sababu\(10\).
- Hoja\(n\) maeneo ya decimal, uongeze zero ikiwa inahitajika.
- Kama exponent ni chanya, hoja decimal uhakika\(n\) maeneo ya haki.
- Kama exponent ni hasi, hoja decimal uhakika\(|n|\) maeneo kwa upande wa kushoto.
- Angalia.
- Ili kubadilisha decimal kwa notation ya kisayansi:
- Hoja uhakika decimal ili sababu ya kwanza ni kubwa kuliko au sawa na\(1\) lakini chini ya\(10\).
- Hesabu idadi ya maeneo ya decimal,\(n\) kwamba hatua ya decimal ilihamishwa.
- Andika namba kama bidhaa yenye nguvu ya\(10\). Ikiwa nambari ya awali ni:
- kubwa kuliko\(1\), nguvu ya\(10\) itakuwa\(10^n\)
- kati\(0\) na\(1\), nguvu ya\(10\) itakuwa\(10^{−n}\)
- Angalia.
faharasa
- mtetezi hasi
- Ikiwa\(n\) ni integer nzuri na\(a \neq 0\), basi\(a^{-n}=\dfrac{1}{a^{n}}\).
- nukuu ya kisayansi
- Nambari inaonyeshwa katika nukuu ya kisayansi wakati ni ya fomu\(a \times 10^{n}\) wapi\(a \geq 1\) na<10 na\(n\) ni integer.


