6.4E: Mazoezi

Last updated
Save as PDF

Page ID: 177888

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Mazoezi hufanya kamili

Mraba Binomial Kutumia Mipangilio ya Mraba ya Binomial

Katika mazoezi yafuatayo, mraba kila binomial kwa kutumia Pattern ya Mraba ya Binomial.

Zoezi 1

$(w+4)^2$

Zoezi la 2

$(q+12)^2$

Jibu: $q^2+24q+144$

Zoezi la 3

$(y+14)^2$

Zoezi la 4

$(x+\frac{2}{3})^2$

Jibu: $x^2+\frac{4}{3}x+\frac{4}{9}$

Zoezi 5

$(b−7)^2$

Zoezi la 6

$(y−6)^2$

Jibu: $y^2−12y+36$

Zoezi la 7

$(m−15)^2$

Zoezi la 8

$(p−13)^2$

Jibu: $p^2−26p+169$

Zoezi la 9

$(3d+1)^2$

Zoezi la 10

$(4a+10)^2$

Jibu: $16a^2+80a+100$

Zoezi 11

$(2q+13)^2$

Zoezi 12

$(3z+15)^2$

Jibu: $9z^2+65z+125$

Zoezi 13

$(3x−y)^2$

Zoezi 14

$(2y−3z)^2$

Jibu: $4y^2−12yz+9z^2$

Zoezi 15

$(15x−17y)^2$

Zoezi 16

$(18x−19y)^2$

Jibu: $164x^2−136xy+181y^2$

Zoezi 17

$(3x2+2)^2$

Zoezi 18

$(5u^2+9)^2$

Jibu: $25u^4+90u^2+81$

Zoezi la 19

$(4y^3−2)^2$

Zoezi la 20

$(8p^3−3)^2$

Jibu: $64p^6−48p^3+9$

Kuzidisha conjugates Kutumia Bidhaa ya Conjugates Pattern

Katika mazoezi yafuatayo, kuzidisha kila jozi ya conjugates kwa kutumia Bidhaa ya Conjugates Pattern.

Zoezi 21

$(m−7)(m+7)$

Zoezi la 22

$(c−5)(c+5)$

Jibu: $c^2−25$

Zoezi 23

$(x+34)(x−34)$

Zoezi 24

$(b+\frac{6}{7})(b−\frac{6}{7})$

Jibu: $b^2−\frac{36}{49}$

Zoezi 25

$(5k+6)(5k−6)$

Zoezi 26

$(8j+4)(8j−4)$

Jibu: $64j^2−16$

Zoezi 27

$(11k+4)(11k−4)$

Zoezi 28

$(9c+5)(9c−5)$

Jibu: $81c^2−25$

Zoezi 29

$(11−b)(11+b)$

Zoezi 30

$(13−q)(13+q)$

Jibu: $169−q^2$

Zoezi 31

$(5−3x)(5+3x)$

Zoezi 32

$(4−6y)(4+6y)$

Jibu: $16−36y^2$

Zoezi la 33

$(9c−2d)(9c+2d)$

Zoezi 34

$(7w+10x)(7w−10x)$

Jibu: $49w^2−100x^2$

Zoezi 35

$(m+\frac{2}{3}n)(m−\frac{2}{3}n)$

Zoezi 36

$(p+\frac{4}{5}q)(p−\frac{4}{5}q)$

Jibu: $p^2−\frac{16}{25}q^2$

Zoezi 37

$(ab−4)(ab+4)$

Zoezi 38

$(xy−9)(xy+9)$

Jibu: $x^{2}y^2−81$

Zoezi 39

$(uv−\frac{3}{5})(uv+\frac{3}{5})$

Zoezi 40

$(rs−\frac{2}{7})(rs+\frac{2}{7})$

Jibu: $r^{2}s^2−\frac{4}{49}$

Zoezi 41

$(2x^2−3y^4)(2x^2+3y^4)$

Zoezi 42

$(6m^3−4n^5)(6m^3+4n^5)$

Jibu: $36m^6−16n^{10}$

Zoezi 43

$(12p^3−11q^2)(12p^3+11q^2)$

Zoezi 44

$(15m^2−8n^4)(15m^2+8n^4)$

Jibu: $225m^4−64n^8$

Tambua na Tumia Pattern maalum ya Bidhaa

Katika mazoezi yafuatayo, tafuta kila bidhaa.

Zoezi 45

a.$(p−3)(p+3)$

b.$(t−9)^2$

c.$(m+n)^2$

d.$(2x+y)(x−2y)$

Zoezi 46

a.$(2r+12)^2$

b.$(3p+8)(3p−8)$

c.$(7a+b)(a−7b)$

d.$(k−6)^2$

Jibu

a.$4r^2+48r+144$

b.$9p^2−64$

c.$7a^2−48ab−7b^2$

d.$k^2−12k+36$

Zoezi 47

a.$(a^5−7b)^2$

b.$(x^2+8y)(8x−y^2)$

c.$(r^6+s^6)(r^6−s^6)$

d.$(y^4+2z)^2$

Zoezi 48

a.$(x^5+y^5)(x^5−y^5)$

b.$(m^3−8n)^2$

c.$(9p+8q)^2$

d.$(r^2−s^3)(r^3+s^2)$

Jibu: a.$x^{10}−y^{10}$

b.$m^6−16m^{3}n+64n^2$

c.$81p^2+144pq+64q^2$

d.$r^5+r^{2}s^2−r^{3}s^3−s^5$

kila siku Math

Zoezi 49

Math ya akili Unaweza kutumia bidhaa za muundo wa conjugates kuzidisha idadi bila calculator. Sema unahitaji kuzidisha mara 47 53. Fikiria 47 kama 50—3 na 53 kama 50+3

Kuzidisha (50—3) (50+3) kwa kutumia bidhaa ya muundo wa conjugates,$(a−b)(a+b)=a^2−b^2$
Kuzidisha 47·53 bila kutumia calculator.
Njia ipi ni rahisi kwako? Kwa nini?

Zoezi 50

Hesabu ya akili Unaweza kutumia muundo wa mraba wa binomial kuzidisha idadi bila calculator. Sema unahitaji mraba 65. Fikiria 65 kama 60+5.

Kuzidisha$(60+5)^2$ kwa kutumia muundo wa mraba wa binomial,$(a+b)^2=a^2+2ab+b^2$
Mraba 65 bila kutumia calculator.
Njia ipi ni rahisi kwako? Kwa nini?

Jibu

4,225
4,225
Majibu yatatofautiana.

Mazoezi ya kuandika

Zoezi 51

Je, unaamuaje muundo gani wa kutumia?

Zoezi 52

Kwa nini$(a+b)^2$ husababisha trinomial, lakini (a-b) (a+b) husababisha binomial?

Jibu: Majibu yatatofautiana.

Zoezi 53

Marta alifanya kazi zifuatazo kwenye karatasi yake ya nyumbani:

\[\begin{array}{c} {(3−y)^2}\\ {3^2−y^2}\\ {9−y^2}\\ \nonumber \end{array}\]

Eleza ni nini kibaya na kazi ya Marta.

Zoezi 54

Tumia utaratibu wa shughuli ili kuonyesha kuwa$(3+5)^2$ ni 64, halafu utumie mfano huo wa namba ili kuelezea kwa nini$(a+b)^2 \ne a^2+b^2$

Jibu: Majibu yatatofautiana.

Self Check

ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

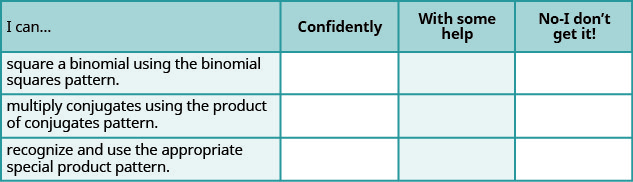
$Hii ni meza ambayo ina safu nne na nguzo nne. Katika mstari wa kwanza, ambayo ni mstari wa kichwa, seli zinasoma kutoka kushoto kwenda kulia “Ninaweza...,” “Kwa ujasiri,” “Kwa msaada fulani,” na “Hakuna-Siipati!” Safu ya kwanza chini ya “I can...” inasomeka “mraba binomial kwa kutumia muundo wa mraba wa binomial,” “kuzidisha conjugates kwa kutumia bidhaa za muundo wa conjugates,” na “kutambua na kutumia muundo sahihi wa bidhaa maalum.” Wengine wa seli ni tupu.$

ⓑ Kwa kiwango cha 1-10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?