Skip to main content
Global

6.4: Bidhaa maalum

  1. Last updated
  2. Save as PDF
  • Page ID
    177869

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Mraba, binomial kwa kutumia Pattern ya Mraba ya Binomial
    • Kuzidisha conjugates kwa kutumia Bidhaa ya Conjugates Pattern
    • Kutambua na kutumia muundo sahihi wa bidhaa maalum
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    Kurahisisha: a.\(9^2\) b.\((−9)^2\) c\(−9^2\).

    Ikiwa umekosa tatizo hili, tathmini Zoezi 1.5.13.

    Mraba Binomial Kutumia Mipangilio ya Mraba ya Binomial

    Wataalamu wa hisabati wanapenda kutafuta ruwaza ambazo zitafanya kazi yao iwe rahisi. Mfano mzuri wa hii ni mraba wa binomials. Wakati unaweza daima kupata bidhaa kwa kuandika binomial mara mbili na kutumia njia za sehemu ya mwisho, kuna kazi ndogo ya kufanya ikiwa unajifunza kutumia mfano.

    \[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]

    Angalia matokeo haya. Je! Unaona mwelekeo wowote?

    Nini kuhusu idadi ya maneno? Katika kila mfano sisi squared binomial na matokeo ilikuwa trinomial.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Sasa angalia muda wa kwanza katika kila matokeo. Ilitoka wapi?

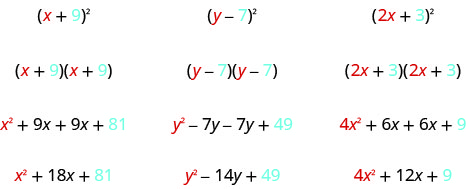
    Takwimu hii ina nguzo tatu. Safu ya kwanza ina maneno x pamoja na 9, katika mabano, mraba. Chini hii ni bidhaa ya x plus 9 na x plus 9. Chini hii ni x squared pamoja 9x pamoja 9x pamoja na 81. Chini hii ni x squared pamoja na 18x pamoja na 81. Safu ya pili ina maneno y minus 7, katika mabano, mraba. Chini ya hii ni bidhaa ya y minus 7 na y minus 7. Chini ya hii ni y squared minus 7y minus 7y pamoja na 49. Chini ya hii ni maneno y squared minus 14y pamoja na 49. Safu ya tatu ina maneno 2x pamoja na 3, katika mabano, mraba. Chini hii ni bidhaa ya 2x pamoja na 3 na 2x pamoja 3. Chini hii ni 4x squared pamoja 6x pamoja 6x pamoja na 9. Chini hii ni 4x squared pamoja na 12x pamoja 9.

    Neno la kwanza ni bidhaa ya maneno ya kwanza ya kila binomial. Kwa kuwa binomials ni sawa, ni mraba wa muda wa kwanza!

    \[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Ili kupata muda wa kwanza wa bidhaa, mraba mrefu wa kwanza.

    Muda wa mwisho ulitoka wapi? Angalia mifano na upate mfano.

    Muda wa mwisho ni bidhaa ya maneno ya mwisho, ambayo ni mraba wa muda wa mwisho.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]

    Ili kupata muda wa mwisho wa bidhaa, mraba muda wa mwisho.

    Hatimaye, angalia muda wa kati. Angalia ilitoka kwa kuongeza maneno ya “nje” na “ndani” ambayo ni sawa! Hivyo muda wa kati ni mara mbili ya bidhaa ya maneno mawili ya binomial.

    \[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]

    \[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]

    Ili kupata muda wa kati wa bidhaa, kuzidisha maneno na bidhaa zao mara mbili.

    Kuweka yote pamoja:

    Binomial Square Pattern

    Ikiwa\(a\) na\(b\) ni namba halisi, muundo wa mraba wa binomial ni

    \[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2}  +  \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]

    Kutumia hii kwa aina mbili za binomial:

    \[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]

    Kwa mraba binomial:

    1. mraba - muda wa kwanza
    2. mraba - muda wa mwisho
    3. mara mbili ya bidhaa zao

    Mfano wa nambari husaidia kuthibitisha muundo.

    \(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)

    Ili kuzidisha\((10+4)^2\) kawaida ungependa kufuata Amri ya Uendeshaji.

    \[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]

    mfano kazi!

    Mfano\(\PageIndex{1}\)

    \(\text { Multiply: }(x+5)^{2}\)

    Suluhisho:

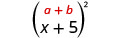      x pamoja na 5, katika mabano, mraba. Zaidi ya maneno ni formula ya jumla pamoja na b, katika mabano, mraba.
    Square muda wa kwanza. x mraba pamoja na tupu pamoja na tupu. Zaidi ya maneno ni fomu ya jumla ya mraba pamoja na 2 b pamoja na b squared.
    Square muda wa mwisho. x mraba pamoja na tupu plus 5 squared.
    Mara mbili ya bidhaa. x squared pamoja na mara 2 x mara 5 pamoja na 5 squared. Zaidi ya maneno haya ni formula ya jumla ya mraba pamoja na mara 2 kwa mara b pamoja na b squared.
    Kurahisisha. \(x^{2}+10 x+25\)
    Jaribu! \(\PageIndex{1}\)

    Kuzidisha:\((x+9)^{2}\)

    Jibu

    \(x^{2}+18 x+81\)

    Jaribu! \(\PageIndex{2}\)

    Kuzidisha:\((y+11)^{2}\)

    Jibu

    \(y^{2}+22 y+121\)

    Mfano\(\PageIndex{2}\)

    Kuzidisha:\((y-3)^{2}\)

    Suluhisho:

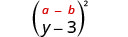      y minus 3, katika mabano, mraba. Zaidi ya maneno ni formula ya jumla ya b, katika mabano, mraba.
    Square muda wa kwanza. y squared minus tupu pamoja na tupu. Zaidi ya maneno ni fomu ya jumla ya mraba pamoja na 2 b pamoja na b squared.
    Square muda wa mwisho. y squared minus tupu pamoja 3 squared.
    Mara mbili ya bidhaa. 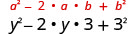y squared minus y mara y mara 3 pamoja na 3 mraba. Zaidi ya maneno haya ni formula ya jumla ya mraba pamoja na mara 2 kwa mara b pamoja na b squared.
    Kurahisisha. \(y^{2}-6 y+9\)
    Jaribu! \(\PageIndex{3}\)

    Kuzidisha:\((x-9)^{2}\)

    Jibu

    \(x^{2}-18 x+81\)

    Jaribu! \(\PageIndex{4}\)

    Kuzidisha:\((p-13)^{2}\)

    Jibu

    \(p^{2}-26 p+169\)

    Mfano\(\PageIndex{3}\)

    Kuzidisha:\((4 x+6)^{2}\)

    Suluhisho:

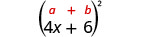      4 x pamoja na 6, katika mabano, mraba. Zaidi ya maneno ni formula ya jumla pamoja na b, katika mabano, mraba.
    Tumia mfano. 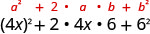4 x mraba pamoja na mara 2 4 x mara 6 pamoja na 6 mraba. Zaidi ya maneno haya ni formula ya jumla ya mraba pamoja na mara 2 kwa mara b pamoja na b squared.
    Kurahisisha. \(16 x^{2}+48 x+36\)
    Jaribu! \(\PageIndex{5}\)

    Kuzidisha:\((6 x+3)^{2}\)

    Jibu

    \(36 x^{2}+36 x+9\)

    Jaribu! \(\PageIndex{6}\)

    Kuzidisha:\((4 x+9)^{2}\)

    Jibu

    \(16 x^{2}+72 x+81\)

    Mfano\(\PageIndex{4}\)

    Kuzidisha:\((2 x-3 y)^{2}\)

    Suluhisho:

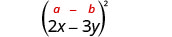      ina 2 x minus 3 y, katika mabano, mraba. Zaidi ya maneno ni formula ya jumla pamoja na b, katika mabano, mraba.
    Tumia mfano. 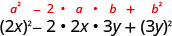2 x mraba minus 2 mara 2 x 3 y pamoja na 3 y squared. Zaidi ya maneno haya ni formula ya jumla ya mraba minus mara 2 kwa mara b pamoja na b squared.
    Kurahisisha. \(4 x^{2}-12 x y+9 y^{2}\)
    Jaribu! \(\PageIndex{7}\)

    Kuzidisha:\((2 c-d)^{2}\)

    Jibu

    \(4 c^{2}-4 c d+d^{2}\)

    Jaribu! \(\PageIndex{8}\)

    Kuzidisha:\((4 x-5 y)^{2}\)

    Jibu

    \(16 x^{2}-40 x y+25 y^{2}\)

    Mfano\(\PageIndex{5}\)

    Kuzidisha:\(\left(4 u^{3}+1\right)^{2}\)

    Suluhisho:

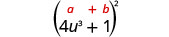      4 u cubed pamoja na 1, katika mabano, mraba. Zaidi ya maneno ni formula ya jumla pamoja na b, katika mabano, mraba.
    Tumia mfano. 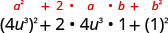4 u cubed, katika mabano, mraba, pamoja na mara 2 4 u mara cubed 1 pamoja 1 mraba. Zaidi ya maneno haya ni formula ya jumla ya mraba pamoja na mara 2 kwa mara b pamoja na b squared.
    Kurahisisha. \(16 u^{6}+8 u^{3}+1\)
    Jaribu! \(\PageIndex{9}\)

    Kuzidisha:\(\left(2 x^{2}+1\right)^{2}\)

    Jibu

    \(4 x^{4}+4 x^{2}+1\)

    Jaribu! \(\PageIndex{10}\)

    Kuzidisha:\(\left(3 y^{3}+2\right)^{2}\)

    Jibu

    \(9 y^{6}+12 y^{3}+4\)

    Kuzidisha conjugates Kutumia Bidhaa ya Conjugates Pattern

    Sisi tu kuona mfano kwa ajili ya squaring binomials kwamba tunaweza kutumia kufanya kuzidisha baadhi binomials rahisi. Vile vile, kuna mfano wa bidhaa nyingine ya binomials. Lakini kabla ya kupata hiyo, tunahitaji kuanzisha msamiati fulani.

    Unaona nini kuhusu jozi hizi za binomials?

    \[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]

    Angalia muda wa kwanza wa kila binomial katika kila jozi.

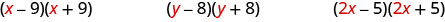
    Takwimu hii ina bidhaa tatu. Ya kwanza ni x minus 9, katika mabano, mara x pamoja na 9, katika mabano. Ya pili ni y minus 8, katika mabano, mara y pamoja na 8, katika mabano. Mwisho ni 2x minus 5, katika mabano, mara 2x pamoja na 5, katika mabano

    Angalia maneno ya kwanza ni sawa katika kila jozi.

    Angalia masharti ya mwisho ya kila binomial katika kila jozi.

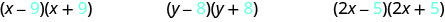
    Takwimu hii ina bidhaa tatu. Ya kwanza ni x minus 9, katika mabano, mara x pamoja na 9, katika mabano. Ya pili ni y minus 8, katika mabano, mara y pamoja na 8, katika mabano. Mwisho ni 2x minus 5, katika mabano, mara 2x pamoja na 5, katika mabano.

    Angalia maneno ya mwisho ni sawa katika kila jozi.

    Angalia jinsi kila jozi ina jumla moja na tofauti moja.

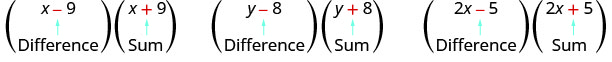
    Takwimu hii ina bidhaa tatu. Ya kwanza ni x minus 9, katika mabano, mara x pamoja na 9, katika mabano. Chini ya x minus 9 ni neno “tofauti”. Chini x pamoja na 9 ni neno “jumla”. Ya pili ni y minus 8, katika mabano, mara y pamoja na 8, katika mabano. Chini y minus 8 ni neno “tofauti”. Chini y pamoja na 8 ni neno “jumla”. Mwisho ni 2x minus 5, katika mabano, mara 2x pamoja na 5, katika mabano. Chini ya 2x minus 5 ni neno “tofauti” na chini ya 2x pamoja na 5 ni neno “jumla”.

    jozi ya binomials kwamba kila mmoja na huo wa kwanza mrefu na huo mwisho mrefu, lakini moja ni jumla na moja ni tofauti ina jina maalum. Inaitwa jozi ya conjugate na ni ya fomu (a-b), (a+b).

    Ufafanuzi: Jozi ya conjugate

    Jozi ya conjugate ni binomials mbili za fomu

    \[(a-b),(a+b)\nonumber \]

    Jozi ya binomials kila mmoja huwa na muda huo wa kwanza na mrefu huo wa mwisho, lakini binomial moja ni jumla na nyingine ni tofauti.

    Kuna mfano mzuri wa kutafuta bidhaa za conjugates. Unaweza, bila shaka, tu FOIL kupata bidhaa, lakini kutumia mfano hufanya kazi yako iwe rahisi.

    Hebu tuangalie mfano kwa kutumia FOIL ili kuzidisha jozi fulani za conjugate.

    \[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]

    Kila neno la kwanza ni bidhaa ya maneno ya kwanza ya binomials, na kwa kuwa yanafanana ni mraba wa muda wa kwanza.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]

    Muda wa mwisho ulikuja kutokana na kuzidisha masharti ya mwisho, mraba wa muda wa mwisho.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]

    Unachunguza nini kuhusu bidhaa?

    Bidhaa ya binomials mbili pia ni binomial! Bidhaa nyingi zinazosababishwa na FOIL zimekuwa za trinomials.

    Kwa nini hakuna muda wa kati? Angalia maneno mawili ya kati unayopata kutoka FOIL yanachanganya hadi 0 katika kila kesi, matokeo ya kuongeza moja na kuondoa moja.

    Bidhaa ya conjugates daima ni ya fomu\(a^2-b^2\). Hii inaitwa tofauti ya mraba.

    Hii inasababisha muundo:

    BIDHAA YA MUUNDO WA CONJUGATES

    Kama\(a\) na\(b\) ni idadi halisi,

    Takwimu hii imegawanywa katika pande mbili. Kwenye upande wa kushoto ni formula ifuatayo: bidhaa ya bala b na b pamoja ni sawa na mraba bala b squared. Kwenye upande wa kulia ni formula sawa iliyoandikwa: minus b na b pamoja ni kinachoitwa “conjugates”, mraba na b mraba ni lebo mraba na ishara ndogo kati ya mraba ni kinachoitwa “tofauti”. Kwa hiyo, bidhaa ya conjugates mbili inaitwa tofauti ya mraba.

    Bidhaa inaitwa tofauti ya mraba.

    Ili kuzidisha conjugates, mraba mrefu wa kwanza, mraba mrefu wa mwisho, na kuandika bidhaa kama tofauti ya mraba.

    Hebu tuchunguze mfano huu kwa mfano wa namba.

    \(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)

    Angalia, matokeo ni sawa!

    Mfano\(\PageIndex{6}\)

    Kuzidisha:\((x-8)(x+8)\)

    Suluhisho:

    Kwanza, kutambua hili kama bidhaa ya conjugates. Binomials zina maneno sawa ya kwanza, na maneno sawa ya mwisho, na binomial moja ni jumla na nyingine ni tofauti.

    Inafaa mfano. 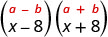Bidhaa ya x minus 8 na x pamoja na 8. Juu ya hii ni fomu ya jumla ya b, katika mabano, mara pamoja na b, katika mabano.
    Square muda wa kwanza, x. 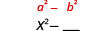x mraba minus tupu. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Square muda wa mwisho, 8. 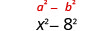x mraba minus 8 mraba.
    Bidhaa ni tofauti ya mraba. 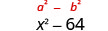x mraba minus 64.
    Jaribu! \(\PageIndex{11}\)

    Kuzidisha:\((x-5)(x+5)\)

    Jibu

    \(x^{2}-25\)

    Jaribu! \(\PageIndex{12}\)

    Kuzidisha:\((w-3)(w+3)\)

    Jibu

    \(w^{2}-9\)

    Mfano\(\PageIndex{7}\)

    Kuzidisha:\((2 x+5)(2 x-5)\)

    Suluhisho:

    Je, binomials hujiunga?

    Ni bidhaa ya conjugates. 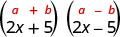Bidhaa ya 2x pamoja na 5 na 2x minus 5. Juu ya hii ni fomu ya jumla ya b, katika mabano, mara pamoja na b, katika mabano.
    Square muda wa kwanza, 2 x. 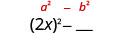2 x mraba minus tupu. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Square muda wa mwisho, 5. 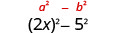2 x mraba minus 5 mraba.
    Kurahisisha. Bidhaa ni tofauti ya mraba. 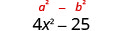4 x mraba minus 25.
    Jaribu! \(\PageIndex{13}\)

    Kuzidisha:\((6 x+5)(6 x-5)\)

    Jibu

    \(36 x^{2}-25\)

    Jaribu! \(\PageIndex{14}\)

    Kuzidisha:\((2 x+7)(2 x-7)\)

    Jibu

    \(4 x^{2}-49\)

    Binomials katika mfano unaofuata inaweza kuangalia nyuma - kutofautiana ni katika kipindi cha pili. Lakini binomials mbili bado ni conjugates, hivyo sisi kutumia mfano huo kuzidisha yao.

    Mfano\(\PageIndex{8}\)

    Pata bidhaa:\((3+5 x)(3-5 x)\)

    Suluhisho:

    Ni bidhaa ya conjugates. 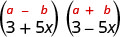Bidhaa ya 3 pamoja na 5 x na 3 minus 5 x Juu ya hii ni fomu ya jumla pamoja b, katika mabano, mara bala b, katika mabano.
    Tumia mfano. 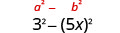3 mraba minus 5 x mraba. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Kurahisisha. \(9-25 x^{2}\)
    Jaribu! \(\PageIndex{15}\)

    Kuzidisha:\((7+4 x)(7-4 x)\)

    Jibu

    \(49-16 x^{2}\)

    Jaribu! \(\PageIndex{16}\)

    Kuzidisha:\((9-2 y)(9+2 y)\)

    Jibu

    \(81-4 y^{2}\)

    Sasa tutaweza kuzidisha conjugates kwamba kuwa na vigezo mbili.

    Mfano\(\PageIndex{9}\)

    Pata bidhaa:\((5 m-9 n)(5 m+9 n)\)

    Suluhisho:

    Hii inafaa mfano. 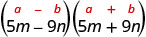5 m minus 9 n na 5 m pamoja na 9 n Juu ya hii ni fomu ya jumla pamoja na b, katika mabano, mara bala b, katika mabano.
    Tumia mfano. 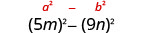5 m mraba minus 9 n squared. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Kurahisisha. \(25 m^{2}-81 n^{2}\)
    Jaribu! \(\PageIndex{17}\)

    Pata bidhaa:\((4 p-7 q)(4 p+7 q)\)

    Jibu

    \(16 p^{2}-49 q^{2}\)

    Jaribu! \(\PageIndex{18}\)

    Pata bidhaa:\((3 x-y)(3 x+y)\)

    Jibu

    \(9 x^{2}-y^{2}\)

    Mfano\(\PageIndex{10}\)

    Pata bidhaa:\((c d-8)(c d+8)\)

    Suluhisho:

    Hii inafaa mfano. 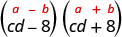Bidhaa ya c d minus 8 na c d pamoja na 8. Zaidi ya hii ni fomu ya jumla pamoja na b, katika mabano, mara bala b, katika mabano.
    Tumia mfano. 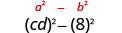c d mraba minus 8 mraba. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Kurahisisha. \(c^{2} d^{2}-64\)
    Jaribu! \(\PageIndex{19}\)

    Pata bidhaa:\((x y-6)(x y+6)\)

    Jibu

    \(x^{2} y^{2}-36\)

    Jaribu! \(\PageIndex{20}\)

    Pata bidhaa:\((a b-9)(a b+9)\)

    Jibu

    \(a^{2} b^{2}-81\)

    Mfano\(\PageIndex{11}\)

    Pata bidhaa:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)

    Suluhisho:

    Hii inafaa mfano. 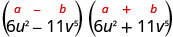Bidhaa ya 6 u squared minus 11 v kwa nguvu ya tano na 6 u squared pamoja 11 v kwa nguvu ya tano. Zaidi ya hii ni fomu ya jumla pamoja na b, katika mabano, mara bala b, katika mabano.
    Tumia mfano. 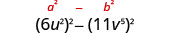6 u squared, katika mabano, mraba, bala 11 v kwa nguvu ya tano, katika mabano, mraba. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Kurahisisha. \(36 u^{4}-121 v^{10}\)
    Jaribu! \(\PageIndex{21}\)

    Pata bidhaa:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)

    Jibu

    \(9 x^{4}-16 y^{6}\)

    Jaribu! \(\PageIndex{22}\)

    Pata bidhaa:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)

    Jibu

    \(4 m^{4}-25 n^{6}\)

    Tambua na Tumia Pattern maalum ya Bidhaa

    Tulianzisha tu mifumo maalum ya bidhaa kwa Mraba ya Binomial na kwa Bidhaa ya Conjugates. Bidhaa zinaonekana sawa, kwa hiyo ni muhimu kutambua wakati ni sahihi kutumia kila moja ya mifumo hii na kutambua jinsi tofauti. Angalia mifumo miwili pamoja na uangalie kufanana na tofauti zao.

    KULINGANISHA MWELEKEO MAALUM WA BIDHAA

    \(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)

    Mfano\(\PageIndex{12}\)

    Chagua muundo unaofaa na uitumie ili kupata bidhaa:

    1. \((2 x-3)(2 x+3)\)
    2. \((8 x-5)^{2}\)
    3. \((6 m+7)^{2}\)
    4. \((5 x-6)(6 x+5)\)

    Suluhisho:

    1. \((2x−3)(2x+3)\)Hizi ni conjugates. Wana idadi sawa ya kwanza, na namba sawa za mwisho, na binomial moja ni jumla na nyingine ni tofauti. Inafaa mfano wa Bidhaa ya Conjugates.

    Hii inafaa mfano. 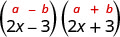Bidhaa ya 2 x minus 3 na 2 x pamoja 3. Zaidi ya hii ni fomu ya jumla pamoja na b, katika mabano, mara bala b, katika mabano.
    Tumia mfano. 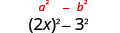2 x mraba minus 3 mraba. Juu ya hii ni fomu ya jumla ya mraba bala b squared.
    Kurahisisha. \(4 x^{2}-9\)

    2. \((8 x-5)^{2}\)Tunaulizwa mraba binomial. Inafaa muundo wa mraba wa binomial.

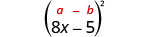      8 x minus 5, katika mabano, mraba. Zaidi ya hii ni fomu ya jumla ya b, katika mabano, mraba.
    Tumia mfano. 8 x mraba minus mara 2 8 x mara 5 pamoja na 5 squared. Zaidi ya hii ni fomu ya jumla ya mraba 2 b pamoja na b squared.
    Kurahisisha. \(64 x^{2}-80 x+25\)

    3. \((6 m+7)^{2}\)Tena, sisi mraba binomial hivyo sisi kutumia binomial mraba mfano.

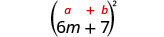      6 m pamoja na 7, katika mabano, mraba. Zaidi ya hii ni fomu ya jumla pamoja na b, katika mabano, mraba.
    Tumia mfano. 6 m mraba pamoja na mara 2 6 m mara 7 pamoja na 7 mraba. Zaidi ya hii ni fomu ya jumla ya mraba pamoja na 2 b pamoja na b squared.
    Kurahisisha. \(36 m^{2}+84 m+49\)

    4. \((5 x-6)(6 x+5)\)Bidhaa hii haifai mwelekeo, kwa hiyo tutatumia FOIL.

    \(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)

    Jaribu! \(\PageIndex{23}\)

    Chagua muundo unaofaa na uitumie ili kupata bidhaa:

    1. \((9b−2)(2b+9)\)
    2. \((9p−4)2\)
    3. \((7y+1)^2\)
    4. \((4r-3)(4r+3)\)
    Jibu
    1. FOIL;\(18 b^{2}+77 b-18\)
    2. Viwanja vya Binomial;\(81 p^{2}-72 p+16\)
    3. Viwanja vya Binomial;\(49 y^{2}+14 y+1\)
    4. Bidhaa ya Conjugates;\(16 r^{2}-9\)
    Jaribu! \(\PageIndex{24}\)

    Chagua muundo unaofaa na uitumie ili kupata bidhaa:

    1. \((6x+7)^2\)
    2. \((3x−4)(3x+4)\)
    3. \((2x−5)(5x−2)\)
    4. \((6n−1)^2\)
    Jibu
    1. Viwanja vya Binomial;\(36 x^{2}+84 x+49\)
    2. Bidhaa ya Conjugates;\(9 x^{2}-16\)
    3. FOIL;\(10 x^{2}-29 x+10\)
    4. Viwanja vya Binomial;\(36 n^{2}-12 n+1\)
    Kumbuka

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na bidhaa maalum:

    • Bidhaa Maalum

    Dhana muhimu

    • Binomial Mraba Pattern
      • Kama, b ni idadi halisi,
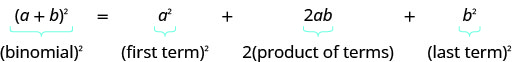
        Hakuna Nakala ya Alt
      • \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
      • \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
      • Kwa mraba binomial: mraba mrefu wa kwanza, mraba mrefu wa mwisho, mara mbili ya bidhaa zao.
    • Bidhaa ya Conjugates Pattern
      • Kama, ba, b ni idadi halisi,
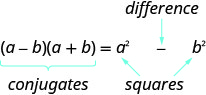
        Hakuna Nakala ya Alt
      • \((a-b)(a+b)=a^{2}-b^{2}\)
      • Bidhaa inaitwa tofauti ya mraba.
    • Ili kuzidisha conjugates:
      • mraba wa kwanza mrefu mraba mrefu wa mwisho kuandika kama tofauti ya mraba

    faharasa

    jozi conjugate
    Jozi ya conjugate ni binomials mbili za fomu\((a−b)\) na\((a+b)\); jozi ya binomials kila mmoja huwa na muda huo wa kwanza na mrefu huo wa mwisho, lakini binomial moja ni jumla na nyingine ni tofauti.