6.5: Gawanya Monomials
- Page ID
- 177805
Mwishoni mwa sehemu hii, utaweza:
- Kurahisisha maneno kwa kutumia Mali Quotient kwa Exponents
- Kurahisisha maneno na watazamaji sifuri
- Kurahisisha maneno kwa kutumia quotient kwa Power Mali
- Kurahisisha maneno kwa kutumia mali kadhaa
- Gawanya monomials
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kurahisisha:\(\dfrac{8}{24}\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.6.4. - Kurahisisha:\((2m^3)^5\).
Kama amekosa tatizo hili, kupitia Zoezi 6.2.22. - kurahisisha:\(\dfrac{12x}{12y}\)
Kama amekosa tatizo hili, kupitia Zoezi 1.6.10.
Kurahisisha Maneno Kutumia Mali ya Quotient kwa Watazamaji
Mapema katika sura hii, sisi maendeleo ya mali ya exponents kwa kuzidisha. Sisi muhtasari mali hizi hapa chini.
Ikiwa a na b ni namba halisi, na m na n ni namba nzima, basi
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Sasa tutaangalia mali exponent kwa mgawanyiko. Kumbukumbu ya haraka ya kumbukumbu inaweza kusaidia kabla ya kuanza. Umejifunza kurahisisha sehemu ndogo kwa kugawa mambo ya kawaida kutoka kwa nambari na denominator kwa kutumia Mali sawa ya FRACTIONS. Mali hii pia itakusaidia kufanya kazi na sehemu za algebraic-ambazo pia ni quotients.
Kama, b, na c ni namba nzima ambapo\(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
Kama hapo awali, tutajaribu kugundua mali kwa kuangalia mifano fulani.
\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]
Taarifa, katika kila kesi besi walikuwa sawa na sisi subtracted exponents.
Wakati exponent kubwa ilikuwa katika nambari, tuliachwa na mambo katika nambari.
Wakati exponent kubwa alikuwa katika denominator, tuliachwa na mambo katika denominator - taarifa namba ya 1.
Tunaandika:
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
Hii inasababisha Mali Quotient kwa Exponents.
Kama ni idadi halisi,\(a\neq 0\), na m na n ni idadi nzima, basi
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Mifano michache yenye namba inaweza kusaidia kuthibitisha mali hii.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Kurahisisha:
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Jibu
-
Ili kurahisisha kujieleza kwa quotient, tunahitaji kwanza kulinganisha vielelezo katika nambari na denominator.
1.
Tangu 9> 7, kuna mambo zaidi ya x katika nambari. 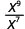
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 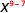
Kurahisisha. \(x^2\) 2.
Kumbuka kwamba wakati exponent kubwa ni katika nambari, sisi ni wa kushoto na mambo katika nambari.Tangu 10> 2, kuna mambo zaidi ya x katika nambari. 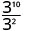
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Kurahisisha. \(3^8\)
Kurahisisha:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Jibu
-
- \(x^{5}\)
- \(6^9\)
Kurahisisha:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Jibu
-
- \(y^{6}\)
- \(10^8\)
Kurahisisha:
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Jibu
-
Ili kurahisisha kujieleza kwa quotient, tunahitaji kwanza kulinganisha vielelezo katika nambari na denominator.
1.
Tangu 12> 8, kuna mambo zaidi ya b katika denominator. 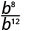
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 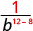
Kurahisisha. 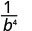
2.
Kumbuka kwamba wakati exponent kubwa ni katika denominator, sisi ni wa kushoto na mambo katika denominator.Tangu 5> 3, kuna mambo zaidi ya 3 katika denominator. 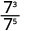
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 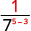
Kurahisisha. 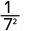
Kurahisisha. 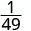
Kurahisisha:
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Jibu
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Kurahisisha:
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Jibu
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Angalia tofauti katika mifano miwili iliyopita:
- Ikiwa tunaanza na mambo zaidi katika nambari, tutaishia na mambo katika nambari.
- Ikiwa tunaanza na mambo zaidi katika denominator, tutaishia na mambo katika denominator.
Hatua ya kwanza katika kurahisisha usemi kwa kutumia Mali ya Quotient kwa Watazamaji ni kuamua kama exponent ni kubwa katika nambari au denominator.
Kurahisisha:
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Jibu
-
1. Je exponent ya kubwa katika nambari au denominator? Tangu 9> 5, kuna zaidi ya a katika denominator na hivyo tutaishia na mambo katika denominator.
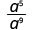
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 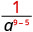
Kurahisisha. 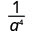
2. Angalia kuna mambo zaidi ya xx katika nambari, tangu 11> 7. Kwa hiyo tutaishia na mambo katika nambari.
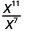
Tumia Mali ya Quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 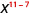
Kurahisisha. 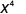
Kurahisisha:
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Jibu
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Kurahisisha:
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Jibu
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Kurahisisha Maneno na Kielelezo cha Zero
Kesi maalum ya Mali ya Quotient ni wakati maonyesho ya nambari na denominator ni sawa, kama vile kujieleza kama\(\dfrac{a^{m}}{a^{m}}\). Kutoka kwa kazi yako ya awali na sehemu ndogo, unajua kwamba:
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
Kwa maneno, idadi iliyogawanywa na yenyewe ni 1. Kwa hiyo\(\dfrac{x}{x}=1\), kwa chochote\(x(x\neq 0)\), kwa kuwa nambari yoyote iliyogawanywa na yenyewe ni 1.
Mali ya Quotient kwa Exponents inatuonyesha jinsi ya kurahisisha\(\dfrac{a^{m}}{a^{n}}\) wakati\(m>n\) na wakati\(n<m\) kwa kutoa exponents. Nini kama\(m=n\)?
Fikiria\(\dfrac{8}{8}\), ambayo tunajua ni 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Sasa sisi kurahisisha\(\dfrac{a^{m}}{a^{m}}\) kwa njia mbili kutuongoza kwa ufafanuzi wa exponent sifuri. Kwa ujumla, kwa\(a\neq 0\):
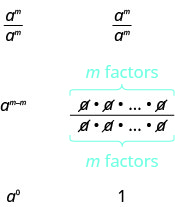
Tunaona\(\dfrac{a^{m}}{a^{m}}\) simplifies\(a^{0}\) na kwa 1. Hivyo\(a^{0} = 1\).
Ikiwa ni nambari isiyo ya sifuri, basi\(a^{0} = 1\).
Nambari yoyote isiyo ya zero iliyoinuliwa kwa nguvu ya sifuri ni 1.
Katika maandishi haya, sisi kudhani variable yoyote kwamba sisi kuongeza kwa nguvu sifuri si sifuri.
Kurahisisha:
- \(9^{0}\)
- \(n^{0}\)
- Jibu
-
Ufafanuzi anasema nambari yoyote isiyo ya sifuri iliyoinuliwa kwa nguvu ya sifuri ni 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Kurahisisha:
- \(15^{0}\)
- \(m^{0}\)
- Jibu
-
- 1
- 1
Kurahisisha:
- \(k^{0}\)
- \(29^{0}\)
- Jibu
-
- 1
- 1
Sasa kwa kuwa tuna defined exponent sifuri, tunaweza kupanua Mali yote ya Exponents ni pamoja na idadi nzima exponents.
Nini kuhusu kuinua maneno kwa nguvu ya sifuri? Hebu tuangalie\((2x)^0\). Tunaweza kutumia bidhaa kwa utawala wa nguvu ili kuandika tena maneno haya.
\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]
Hii inatuambia kwamba yoyote nonzero kujieleza kukulia kwa nguvu sifuri ni moja.
Kurahisisha:
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Jibu
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Kurahisisha:
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Jibu
-
- 1
- 1
Kurahisisha:
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Jibu
-
- 1
- 1
Kurahisisha Maneno Kutumia Quotient kwa Mali ya Nguvu
Sasa tutaangalia mfano ambao utatuongoza kwenye Quotient kwa Mali ya Nguvu.
\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]
Kumbuka kwamba exponent inatumika kwa nambari zote mbili na denominator.
\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]
Hii inasababisha Quotient kwa Power Mali kwa Exponents.
Ikiwa a na b ni namba halisi,\(b\neq 0\), na m ni namba ya kuhesabu, basi
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
Ili kuongeza sehemu kwa nguvu, ongeza nambari na denominator kwa nguvu hiyo.
Mfano na namba inaweza kukusaidia kuelewa mali hii:
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Kurahisisha:
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Jibu
-
1.
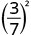
Tumia Mali ya Quotient,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 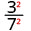
Kurahisisha. 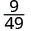
2.
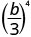
Tumia Mali ya Quotient,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 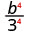
Kurahisisha. 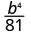
3.

Kuongeza nambari na denominator kwa nguvu ya tatu. 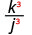
Kurahisisha:
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Jibu
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Kurahisisha:
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Jibu
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Kurahisisha Maneno kwa kutumia Mali kadhaa
Tutaweza sasa muhtasari mali yote ya exponents hivyo wote ni pamoja kwa kutaja kama sisi kurahisisha maneno kwa kutumia mali kadhaa. Kumbuka kwamba wao ni sasa defined kwa exponents idadi nzima.
Ikiwa a na b ni namba halisi, na m na n ni namba nzima, basi
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Kurahisisha:\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Jibu
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Kurahisisha:\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Jibu
-
\(m^{13}\)
Kurahisisha:\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Jibu
-
\(k^{5}\)
Kurahisisha:\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Jibu
-
\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]
Angalia kwamba baada ya sisi rahisi denominator katika hatua ya kwanza, nambari na denominator walikuwa sawa. Hivyo thamani ya mwisho ni sawa na 1.
Kurahisisha\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).
- Jibu
-
1
Kurahisisha\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).
- Jibu
-
1
Kurahisisha:\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Jibu
-
\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]
Kurahisisha:\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Jibu
-
\(r^{8}\)
Kurahisisha:\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Jibu
-
\(v^{6}\)
Kurahisisha:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Jibu
-
Hapa hatuwezi kurahisisha ndani ya mabano kwanza, kwani misingi si sawa.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Kurahisisha:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Jibu
-
\(\dfrac{a^{12}}{b^{8}}\)
Kurahisisha:\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Jibu
-
\(\dfrac{q^{21}}{r^{15}}\)
Kurahisisha:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Jibu
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Kurahisisha:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Jibu
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Kurahisisha:\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Jibu
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Kurahisisha:\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Jibu
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Kurahisisha:\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Jibu
-
\(\dfrac{1}{a^{6}}\)
Kurahisisha:\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Jibu
-
\(\dfrac{1}{p^{15}}\)
Kurahisisha:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Jibu
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Kurahisisha:\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Jibu
-
9\(r^{18}\)
Kurahisisha:\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Jibu
-
\(\dfrac{2}{x}\)
Kugawanya Monomials
Sasa umeanzishwa kwa mali zote za exponents na kuzitumia ili kurahisisha maneno. Kisha, utaona jinsi ya kutumia mali hizi kugawanya monomials. Baadaye, utazitumia kugawanya polynomials.
Pata quotient:\(56 x^{7} \div 8 x^{3}\)
- Jibu
-
\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]
Pata quotient:\(42y^{9} \div 6 y^{3}\)
- Jibu
-
\(7y^{6}\)
Pata quotient:\(48z^{8} \div 8 z^{2}\)
- Jibu
-
\(6z^{6}\)
Pata quotient:\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Jibu
-
Tunapogawanya monomials na variable zaidi ya moja, tunaandika sehemu moja kwa kila kutofautiana.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Pata quotient:\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Jibu
-
\(-\dfrac{9}{a^{5} b}\)
Pata quotient:\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Jibu
-
\(\dfrac{-9 d}{c^{4}}\)
Pata quotient:\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Jibu
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Pata quotient:\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Jibu
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Pata quotient:\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Jibu
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Mara baada ya kuwa ukoo na mchakato na umeifanya hatua kwa hatua mara kadhaa, unaweza kuwa na uwezo wa kurahisisha sehemu katika hatua moja.
Pata quotient:\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Jibu
-
Kuwa makini sana kurahisisha\(\dfrac{14}{21}\) kwa kugawa nje sababu ya kawaida, na kurahisisha vigezo kwa kutoa exponents yao.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Pata quotient:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Jibu
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Pata quotient:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Jibu
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
Katika mifano yote hadi sasa, hapakuwa na kazi ya kufanya katika nambari au denominator kabla ya kurahisisha sehemu. Katika mfano unaofuata, tutapata kwanza bidhaa za monomials mbili katika nambari kabla ya kurahisisha sehemu. Hii ifuatavyo utaratibu wa shughuli. Kumbuka, bar ya sehemu ni ishara ya makundi.
Pata quotient:\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Jibu
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Pata quotient:\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Jibu
-
\(2 a b^{2}\)
Pata quotient:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Jibu
-
\(-4 x y^{5}\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kugawa monomials:
- Maneno ya busara
- Kugawanya Monomials
- Kugawanya Monomials 2
Dhana muhimu
- Quotient Mali kwa ajili ya Exponents:
- Ikiwa ni namba halisi,\(a\neq 0\), na m, n ni namba nzima, basi:\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- sifuri exponent
- Ikiwa ni nambari isiyo ya sifuri, basi\(a^{0} =1\).
- Quotient kwa Power Mali kwa Exponents:
- Ikiwa a na b ni namba halisi,\(b\neq 0\), na mm ni namba ya kuhesabu, basi:\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- Ili kuongeza sehemu kwa nguvu, ongeza nambari na denominator kwa nguvu hiyo.
- Muhtasari wa Mali Exponent
- Ikiwa a, b ni namba halisi na m, nm, n ni namba nzima, basi\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)


