6.1E: Mazoezi
- Page ID
- 177872
Kutambua Polynomials, Monomials, Binomials, na Trinomials
Katika mazoezi yafuatayo, onyesha kama kila moja ya polynomials zifuatazo ni monomial, binomial, trinomial, au polynomial nyingine.
- \(81b^5−24b^3+1\)
- \(5c^3+11c^2−c−8\)
- \(\frac{14}{15}y+\frac{1}{7}\)
- \(5\)
- \(4y+17\)
- Jibu
-
- ya trinomial
- polynomial
- binomial
- monomial
- binomial
- \(x^2−y^2\)
- \(−13c^4\)
- \(x^2+5x−7\)
- \(x^{2}y^2−2xy+8\)
- \(19\)
- \(8−3x\)
- \(z^2−5z−6\)
- \(y^3−8y^2+2y−16\)
- \(81b^5−24b^3+1\)
- \(−18\)
- Jibu
-
- binomial
- ya trinomial
- polynomial
- ya trinomial
- monomial
- \(11y^2\)
- \(−73\)
- \(6x^2−3xy+4x−2y+y^2\)
- \(4y+17\)
- \(5c^3+11c^2−c−8\)
Kuamua Shahada ya Polynomials
Katika mazoezi yafuatayo, tambua kiwango cha kila polynomial.
- \(6a^2+12a+14\)
- \(18xy^{2}z\)
- \(5x+2\)
- \(y^3−8y^2+2y−16\)
- \(−24\)
- Jibu
-
- 2
- 4
- 1
- 3
- 0
- \(9y^3−10y^2+2y−6\)
- \(−12p^4\)
- \(a^2+9a+18\)
- \(20x^{2}y^2−10a^{2}b^2+30\)
- \(17\)
- \(14−29x\)
- \(z^2−5z−6\)
- \(y^3−8y^2+2y−16\)
- \(23ab^2−14\)
- \(−3\)
- Jibu
-
- 1
- 2
- 3
- 3
- 0
- \(62y^2\)
- \(15\)
- \(6x^2−3xy+4x−2y+y^2\)
- \(10−9x\)
- \(m^4+4m^3+6m^2+4m+1\)
Kuongeza na Ondoa Monomials
Katika mazoezi yafuatayo, ongeza au uondoe monomials.
\(7x^2+5x^2\)
- Jibu
-
\(12x^2\)
\(4y^3+6y^3\)
\(−12w+18w\)
- Jibu
-
\(6w\)
\(−3m+9m\)
\(4a−9a\)
- Jibu
-
\(−5a\)
\(−y−5y\)
\(28x−(−12x)\)
- Jibu
-
\(40x\)
\(13z−(−4z)\)
\(−5b−17b\)
- Jibu
-
\(−22b\)
\(−10x−35x\)
\(12a+5b−22a\)
- Jibu
-
\(−10a+5b\)
\(14x−3y−13x\)
\(2a^2+b^2−6a^2\)
- Jibu
-
\(−4a^2+b^2\)
\(5u^2+4v^2−6u^2\)
\(xy^2−5x−5y^2\)
- Jibu
-
\(xy^2−5x−5y^2\)
\(pq^2−4p−3q^2\)
\(a^{2}b−4a−5ab^2\)
- Jibu
-
\(a^{2}b−4a−5ab^2\)
\(x^{2}y−3x+7xy^2\)
\(12a+8b\)
- Jibu
-
\(12a+8b\)
\(19y+5z\)
Ongeza:\(4a,\,−3b,\,−8a\)
- Jibu
-
\(−4a−3b\)
Ongeza:\(4x,\,3y,\,−3x\)
Ondoa\(5x^6\) kutoka\(−12x^6\)
- Jibu
-
\(−17x^6\)
Ondoa\(2p^4\) kutoka\(−7p^4\)
Kuongeza na Ondoa Polynomials
Katika mazoezi yafuatayo, ongeza au uondoe polynomials.
\((5y^2+12y+4)+(6y^2−8y+7)\)
- Jibu
-
\(11y^2+4y+11\)
\((4y^2+10y+3)+(8y^2−6y+5)\)
\((x^2+6x+8)+(−4x^2+11x−9)\)
- Jibu
-
\(−3x^2+17x−1\)
\((y^2+9y+4)+(−2y^2−5y−1)\)
\((8x^2−5x+2)+(3x^2+3)\)
- Jibu
-
\(11x^2−5x+5\)
\((7x^2−9x+2)+(6x^2−4)\)
\((5a^2+8)+(a^2−4a−9)\)
- Jibu
-
\(6a^2−4a−1\)
\((p^2−6p−18)+(2p^2+11)\)
\((4m^2−6m−3)−(2m^2+m−7)\)
- Jibu
-
\(2m^2−7m+4\)
\((3b^2−4b+1)−(5b^2−b−2)\)
\((a^2+8a+5)−(a^2−3a+2)\)
- Jibu
-
\(11a+3\)
\((b^2−7b+5)−(b^2−2b+9)\)
\((12s^2−15s)−(s−9)\)
- Jibu
-
\(12s^2−16s+9\)
\((10r^2−20r)−(r−8)\)
Ondoa\((9x^2+2)\) kutoka\((12x^2−x+6)\)
- Jibu
-
\(3x^2−x+4\)
Ondoa\((5y^2−y+12)\) kutoka\((10y^2−8y−20)\)
Ondoa\((7w^2−4w+2)\) kutoka\((8w^2−w+6)\)
- Jibu
-
\(w^2+3w+4\)
Ondoa\((5x^2−x+12)\) kutoka\((9x^2−6x−20)\)
Kupata jumla ya\((2p^3−8)\) na\((p^2+9p+18)\)
- Jibu
-
\(2p^3+p^2+9p+10\)
Kupata jumla ya
\((q^2+4q+13)\) na\((7q^3−3)\)
Kupata jumla ya\((8a^3−8a)\) na\((a^2+6a+12)\)
- Jibu
-
\(8a^3+a^2−2a+12\)
Kupata jumla ya
\((b^2+5b+13)\) na\((4b^3−6)\)
Kupata tofauti ya
\((w^2+w−42)\)na
\((w^2−10w+24)\).
- Jibu
-
\(11w−66\)
Kupata tofauti ya
\((z^2−3z−18)\) na
\((z^2+5z−20)\)
Kupata tofauti ya
\((c^2+4c−33)\) na
\((c^2−8c+12)\)
- Jibu
-
\(12c−45\)
Kupata tofauti ya
\((t^2−5t−15)\) na
\((t^2+4t−17)\)
\((7x^2−2xy+6y^2)+(3x^2−5xy)\)
- Jibu
-
\(10x^2−7xy+6y^2\)
\((−5x^2−4xy−3y^2)+(2x^2−7xy)\)
\((7m^2+mn−8n^2)+(3m^2+2mn)\)
- Jibu
-
\(10m^2+3mn−8n^2\)
\((2r^2−3rs−2s^2)+(5r^2−3rs)\)
\((a^2−b^2)−(a^2+3ab−4b^2)\)
- Jibu
-
\(−3ab+3b^2\)
\((m^2+2n^2)−(m^2−8mn−n^2)\)
\((u^2−v^2)−(u^2−4uv−3v^2)\)
- Jibu
-
\(4uv+2v^2\)
\((j^2−k^2)−(j^2−8jk−5k^2)\)
\((p^3−3p^{2}q)+(2pq^2+4q^3) −(3p^{2}q+pq^2)\)
- Jibu
-
\(p^3−6p^{2}q+pq^2+4q^3\)
\((a^3−2a^{2}b)+(ab^2+b^3)−(3a^{2}b+4ab^2)\)
\((x^3−x^{2}y)−(4xy^2−y^3)+(3x^{2}y−xy^2)\)
- Jibu
-
\(x^3+2x^{2}y−5xy^2+y^3\)
\((x^3−2x^{2}y)−(xy^2−3y^3)−(x^{2}y−4xy^2)\)
Tathmini Polynomial kwa Thamani iliyotolewa
Katika mazoezi yafuatayo, tathmini kila polynomial kwa thamani iliyotolewa.
Tathmini\(8y^2−3y+2\) wakati:
- \(y=5\)
- \(y=−2\)
- \(y=0\)
- Jibu
-
- \(187\)
- \(46\)
- \(2\)
Tathmini\(5y^2−y−7\) wakati:
- \(y=−4\)
- \(y=1\)
- \(y=0\)
Tathmini\(4−36x\) wakati:
- \(x=3\)
- \(x=0\)
- \(x=−1\)
- Jibu
-
- \(−104\)
- \(4\)
- \(40\)
Tathmini\(16−36x^2\) wakati:
- \(x=−1\)
- \(x=0\)
- \(x=2\)
Mchoraji matone brashi kutoka\(75\) miguu jukwaa juu. Polynomial\(−16t^2+75\) inatoa urefu wa\(t\) sekunde za brashi baada ya kushuka. Pata urefu baada ya\(t=2\) sekunde.
- Jibu
-
\(11\)
Msichana hupiga mpira kwenye mwamba ndani ya bahari. Polynomial\(−16t^2+250\) inatoa urefu wa\(t\) sekunde za mpira baada ya kushuka kutoka kwenye mwamba mrefu wa mguu 250. Pata urefu baada ya\(t=2\) sekunde.
Mtengenezaji wa wasemaji wa sauti ya stereo amegundua kwamba mapato yaliyopatikana kutokana na kuuza wasemaji kwa gharama ya\(p\) dola kila mmoja hutolewa na polynomial\(−4p^2+420p\). Kupata mapato ya kupokea wakati\(p=60\) dola.
- Jibu
-
\($10,800\)
Mtengenezaji wa viatu vya hivi karibuni vya mpira wa kikapu amegundua kwamba mapato yaliyopatikana kutokana na kuuza viatu kwa gharama ya\(p\) dola kila mmoja hutolewa na polynomial\(−4p^2+420p\). Kupata mapato ya kupokea wakati\(p=90\) dola.
kila siku Math
Ufanisi wa mafuta ufanisi wa mafuta (katika maili kwa kila lita) ya gari kwenda kwa kasi ya\(x\) maili kwa saa hutolewa na polynomial\(−\frac{1}{150}x^2+\frac{1}{3}x\), ambapo\(x=30\) mph.
- Jibu
-
\(4\)
Kuacha Umbali Idadi ya miguu inachukua kwa gari kusafiri kwa\(x\) maili kwa saa kuacha juu ya kavu, kiwango halisi hutolewa na polynomial\(0.06x^2+1.1x\), ambapo\(x=40\) mph.
Gharama ya kukodisha Gharama ya kukodisha safi ya rug kwa\(d\) siku hutolewa na polynomial\(5.50d+25\). Pata gharama ya kukodisha safi kwa\(6\) siku.
- Jibu
-
\($58\)
Urefu wa Projectile Urefu (kwa miguu) wa kitu kilichopangwa juu hutolewa na polynomial\(−16t^2+60t+90\) ambapo\(t\) inawakilisha wakati kwa sekunde. Pata urefu baada ya\(t=2.5\) sekunde.
Joto Conversion Joto katika digrii Fahrenheit hutolewa na polynomial\(\frac{9}{5}c+32\) ambapo\(c\) inawakilisha joto katika digrii Celsius. Kupata joto katika digrii Fahrenheit wakati\(c=65°\).
- Jibu
-
\(149°\)F
Mazoezi ya kuandika
Kutumia maneno yako mwenyewe, kuelezea tofauti kati ya monomial, binomial, na trinomial.
Kutumia maneno yako mwenyewe, kuelezea tofauti kati ya polynomial na maneno tano na polynomial yenye shahada ya 5.
- Jibu
-
Majibu yatatofautiana.
Ariana anadhani jumla\(6y^2+5y^4\) ni\(11y^6\)
Jonathan anadhani kwamba\(\frac{1}{3}\) na wote\(\frac{1}{x}\) ni monomials. Ni nini kibaya na hoja zake?
- Jibu
-
Majibu yatatofautiana.
Self Check
Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
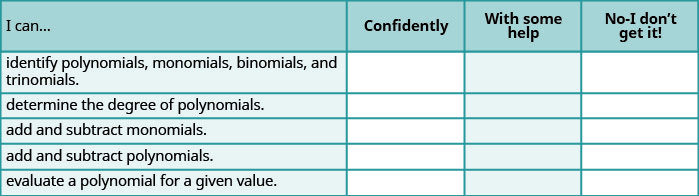
b Kama wengi wa hundi yako walikuwa:
... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.
... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha una msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?
... hapana - Siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.


