6.1: Kuongeza na Ondoa Polynomials

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Kutambua polynomials, monomials, binomials, na trinomials
• Kuamua kiwango cha polynomials
• Ongeza na uondoe monomials
• Ongeza na uondoe polynomials
• Tathmini polynomial kwa thamani iliyotolewa

Quiz

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Kurahisisha:$8x+3x$.
   Kama amekosa tatizo hili, kupitia Zoezi 1.3.37.
2. Ondoa:$(5n+8)−(2n−1)$.
   Kama amekosa tatizo hili, kupitia Zoezi 1.10.52.
3. Andika katika fomu iliyopanuliwa:$a^{5}$.
   Ikiwa umekosa tatizo hili, kagua Zoezi 1.3.7.

Kutambua Polynomials, Monomials, Binomials na Trinomials

Umejifunza kwamba neno ni mara kwa mara au bidhaa ya vigezo vya mara kwa mara na moja au zaidi. Wakati ni wa fomu$ax^{m}$, wapi$a$ mara kwa mara na$m$ ni namba nzima, inaitwa monomial. Baadhi ya mifano ya monomial ni$8,−2x^{2},4y^{3}$, na$11z^{7}$.

Ufafanuzi: Monomials

Monomial ni neno la fomu$ax^{m}$, ambapo$a$ ni mara kwa mara na$m$ ni nambari nzima.

Monomial, au monomials mbili au zaidi pamoja na kuongeza au kuondoa, ni polynomial. Baadhi ya polynomials wana majina maalum, kulingana na idadi ya maneno. Monomial ni polynomial yenye muda mmoja. Binomial ina maneno mawili, na trinomial ina maneno matatu hasa. Hakuna majina maalum ya polynomials yenye maneno zaidi ya tatu.

ufafanuzi: Polynomials

• polynomial -monomial, au monomials mbili au zaidi pamoja na kuongeza au kutoa, ni polynomial.
• monomial -polynomial na neno moja hasa inaitwa monomial.
• binomial —polynomial yenye maneno mawili hasa inaitwa binomial.
• trinomial -polynomial na maneno matatu hasa inaitwa trinomial.

Hapa ni baadhi ya mifano ya polynomials.

$$\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber$$

Angalia kwamba kila monomial, binomial, na trinomial pia ni polynomial. Wao ni wanachama maalum wa “familia” ya polynomials na hivyo wana majina maalum. Tunatumia maneno monomial, binomial, na trinomial wakati akimaanisha polynomials hizi maalum na tu wito wote polynomials wengine.

Mfano$\PageIndex{1}$

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine.

1. $4y^{2}−8y−6$
2. $−5a^{4}b^{2}$
3. $2x^{5}−5x^{3}−3x + 4$
4. $13−5m^{3}$
5. q

Jibu

$\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}$

Mfano$\PageIndex{2}$

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine:

1. 5b
2. $8 y^{3}-7 y^{2}-y-3$
3. $-3 x^{2}-5 x+9$
4. $81-4 a^{2}$
5. $-5 x^{6}$

Jibu

1. monomial
2. polynomial
3. ya trinomial
4. binomial
5. monomial

Mfano$\PageIndex{3}$

Kuamua kama kila polynomial ni monomial, binomial, trinomial, au polynomial nyingine:

1. $27 z^{3}-8$
2. $12 m^{3}-5 m^{2}-2 m$
3. $\frac{5}{6}$
4. $8 x^{4}-7 x^{2}-6 x-5$
5. $-n^{4}$

Jibu

1. binomial
2. ya trinomial
3. monomial
4. polynomial
5. monomial

Kuamua Shahada ya Polynomials

Kiwango cha polynomial na kiwango cha masharti yake ni kuamua na exponents ya variable. Monomial ambayo haina kutofautiana, tu mara kwa mara, ni kesi maalum. Kiwango cha mara kwa mara ni 0, yaani, haina kutofautiana.

Ufafanuzi: Shahada ya Polynomial

• Kiwango cha neno ni jumla ya watazamaji wa vigezo vyake.
• Kiwango cha mara kwa mara ni 0.
• Kiwango cha polynomial ni kiwango cha juu cha masharti yake yote.

Hebu tuone jinsi hii inavyofanya kazi kwa kuangalia polynomials kadhaa. Tutachukua hatua kwa hatua, kuanzia na monomials, na kisha kuendelea kwa polynomials na maneno zaidi.

Polynomial iko katika fomu ya kawaida wakati maneno ya polynomial yameandikwa katika utaratibu wa kushuka kwa digrii. Pata tabia ya kuandika neno kwa shahada ya juu kwanza.

Mfano$\PageIndex{4}$

Pata shahada ya polynomials zifuatazo.

1. 10y
2. $4 x^{3}-7 x+5$
3. -15
4. $-8 b^{2}+9 b-2$
5. $8 x y^{2}+2 y$

Jibu

1. $\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}$
2. $\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}$
3. $\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}$
4. $\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}$
5. $\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}$

Mfano$\PageIndex{5}$

Pata shahada ya polynomials zifuatazo:

1. -15b
2. $10 z^{4}+4 z^{2}-5$
3. $12 c^{5} d^{4}+9 c^{3} d^{9}-7$
4. $3 x^{2} y-4 x$
5. —9

Jibu

1. 1
2. 4
3. 12
4. 3
5. 0

Mfano$\PageIndex{6}$

Pata shahada ya polynomials zifuatazo:

1. 52
2. $a^{4} b-17 a^{4}$
3. $5 x+6 y+2 z$
4. $3 x^{2}-5 x+7$
5. $-a^{3}$

Jibu

1. 0
2. 5
3. 1
4. 2
5. 3

Kuongeza na Ondoa Monomials

Umejifunza jinsi ya kurahisisha maneno kwa kuchanganya maneno kama hayo. Kumbuka, kama maneno lazima kuwa na vigezo sawa na exponent sawa. Kwa kuwa monomials ni maneno, kuongeza na kuondoa monomials ni sawa na kuchanganya maneno kama hayo. Ikiwa monomials ni kama maneno, tunawachanganya tu kwa kuongeza au kuondoa mgawo.

Mfano$\PageIndex{7}$

Ongeza:$25 y^{2}+15 y^{2}$

Jibu

$\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}$

Mfano$\PageIndex{8}$

Ongeza:$12 q^{2}+9 q^{2}$

Jibu

21$q^{2}$

Mfano$\PageIndex{9}$

Ongeza:$-15 c^{2}+8 c^{2}$

Jibu

$-7 c^{2}$

Mfano$\PageIndex{10}$

Ondoa: 16p- (-7p)

Jibu

$\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}$

Mfano$\PageIndex{11}$

Ondoa: 8m-m (-5m).

Jibu

13m

Mfano$\PageIndex{12}$

Ondoa:$-15 z^{3}-\left(-5 z^{3}\right)$

Jibu

$-10 z^{3}$

Kumbuka kwamba kama maneno lazima kuwa na vigezo sawa na exponents sawa.

Mfano$\PageIndex{13}$

Kurahisisha:$c^{2}+7 d^{2}-6 c^{2}$

Jibu

$\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}$

Mfano$\PageIndex{14}$

Ongeza:$8 y^{2}+3 z^{2}-3 y^{2}$

Jibu

$5 y^{2}+3 z^{2}$

Mfano$\PageIndex{15}$

Ongeza:$3 m^{2}+n^{2}-7 m^{2}$

Jibu

$-4 m^{2}+n^{2}$

Mfano$\PageIndex{16}$

Kurahisisha:$u^{2} v+5 u^{2}-3 v^{2}$

Jibu

\ (\ kuanza {safu} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\\ maandishi {2}\\ Nakala {Hakuna maneno kama ya kuchanganya.} & u^ {2} v+5 u^ {2} -3 v^ {2}\ mwisho {safu}\)

Mfano$\PageIndex{17}$

Kurahisisha:$m^{2} n^{2}-8 m^{2}+4 n^{2}$

Jibu

Hakuna maneno kama hayo ya kuchanganya.

Mfano$\PageIndex{18}$

Kurahisisha:$p q^{2}-6 p-5 q^{2}$

Jibu

Hakuna maneno kama hayo ya kuchanganya.

Kuongeza na Ondoa Polynomials

Tunaweza kufikiria kuongeza na kutoa polynomials kama tu kuongeza na kutoa mfululizo wa monomials. Angalia kwa masharti kama-wale walio na vigezo sawa na exponent sawa. Mali ya Comutative inatuwezesha kupanga upya masharti ili kuweka maneno kama pamoja.

Mfano$\PageIndex{19}$

Pata jumla:$\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)$

Jibu

Tambua maneno kama hayo.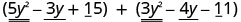
Panga upya ili kupata maneno kama hayo pamoja.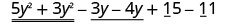
Kuchanganya kama maneno.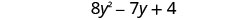

Mfano$\PageIndex{20}$

Pata jumla:$\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)$

Jibu

$8 x^{2}-11 x+1$

Mfano$\PageIndex{21}$

Pata jumla:$\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)$

Jibu

$17 y^{2}+14 y+1$

Mfano$\PageIndex{22}$

Pata tofauti:$\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)$

Jibu

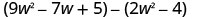
Kusambaza na kutambua maneno kama hayo.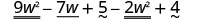
Panga upya masharti.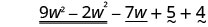
Kuchanganya kama maneno.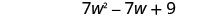

Mfano$\PageIndex{23}$

Pata tofauti:$\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)$

Jibu

$15 x^{2}+3 x-5$

Mfano$\PageIndex{24}$

Pata tofauti:$\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)$

Jibu

$6 b^{2}+3$

Mfano$\PageIndex{25}$

Ondoa:$\left(c^{2}-4 c+7\right)$ kutoka$\left(7 c^{2}-5 c+3\right)$

Jibu

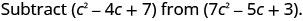
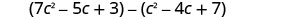
Kusambaza na kutambua maneno kama hayo.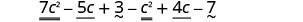
Panga upya masharti.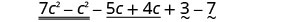
Kuchanganya kama maneno.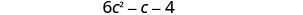

Mfano$\PageIndex{26}$

Ondoa:$\left(5 z^{2}-6 z-2\right)$ kutoka$\left(7 z^{2}+6 z-4\right)$

Jibu

$2 z^{2}+12 z-2$

Mfano$\PageIndex{27}$

Ondoa:$\left(x^{2}-5 x-8\right)$ kutoka$\left(6 x^{2}+9 x-1\right)$

Jibu

$5 x^{2}+14 x+7$

Mfano$\PageIndex{28}$

Pata jumla:$\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)$

Jibu

$\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}$

Mfano$\PageIndex{29}$

Pata jumla:$\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)$

Jibu

$5 x^{2}-5 x y+5 y^{2}$

Mfano$\PageIndex{30}$

Pata jumla:$\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)$

Jibu

$7 x^{2}-6 x y-2 y^{2}$

Mfano$\PageIndex{31}$

Pata tofauti:$\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)$

Jibu

$\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}$

Mfano$\PageIndex{32}$

Pata tofauti:$\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)$

Jibu

$-5 a b-5 b^{2}$

Mfano$\PageIndex{33}$

Pata tofauti:$\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)$

Jibu

$4 n^{2}+7 m n$

Mfano$\PageIndex{34}$

Kurahisisha:$\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)$

Jibu

$\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}$

Mfano$\PageIndex{35}$

Kurahisisha:$\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)$

Jibu

$x^{3}-y^{3}$

Mfano$\PageIndex{36}$

Kurahisisha:$\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)$

Jibu

$p^{3}-2 p^{2} q+q^{3}$

Tathmini Polynomial kwa Thamani iliyotolewa

Tayari tumejifunza jinsi ya kutathmini maneno. Kwa kuwa polynomials ni maneno, tutaweza kufuata taratibu hiyo ya kutathmini polynomial. Tutabadilisha thamani iliyotolewa kwa kutofautiana na kisha kurahisisha kutumia utaratibu wa shughuli.

Mfano$\PageIndex{37}$

Tathmini$5x^{2}−8x+4$ wakati

1. x=4
2. x=—2
3. x=0

Jibu

1. x=4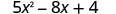
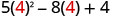
Kurahisisha watetezi.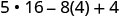
Kuzidisha.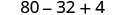
Kurahisisha.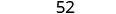

2. x=-1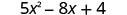
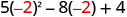
Kurahisisha watetezi.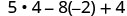
Kuzidisha.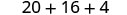
Kurahisisha.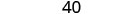

3. x=0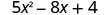
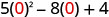
Kurahisisha watetezi.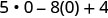
Kuzidisha.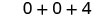
Kurahisisha.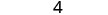

Mfano$\PageIndex{38}$

Tathmini:$3x^{2}+2x−15$ wakati

1. x=3
2. x=-5
3. x=0

Jibu

1. 18
2. 50
3. -15

Mfano$\PageIndex{39}$

Tathmini:$5z^{2}−z−4$ wakati

1. z=—2
2. z=0
3. z=2

Jibu

1. 18
2. —4
3. 14

Mfano$\PageIndex{40}$

Polynomial$−16t^{2}+250$ anatoa urefu wa mpira tt sekunde baada ya imeshuka kutoka 250 mguu mrefu jengo. Pata urefu baada ya sekunde t=2.

Jibu

$\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}$

Mfano$\PageIndex{41}$

Polynomial$−16t^{2}+250$ anatoa urefu wa mpira tt sekunde baada ya imeshuka kutoka 250 mguu mrefu jengo. Pata urefu baada ya sekunde t=0.

Jibu

250

Mfano$\PageIndex{42}$

Polynomial$−16t^{2}+250$ inatoa urefu wa mpira tt sekunde baada ya imeshuka kutoka 250 mguu mrefu jengo. Pata urefu baada ya sekunde t=3.

Jibu

106

Mfano$\PageIndex{43}$

Polynomial$6x^{2}+15xy$ inatoa gharama, kwa dola, ya kuzalisha chombo mstatili ambao juu na chini ni mraba na upande x miguu na pande za urefu y miguu. Pata gharama ya kuzalisha sanduku yenye futi x=4 na y=6y=futi 6.

Jibu

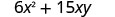
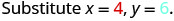
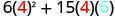
Kurahisisha.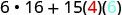
Kurahisisha.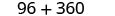
Kurahisisha.
	Gharama ya kuzalisha sanduku ni $456.

Mfano$\PageIndex{43}$

Polynomial$6x^{2}+15xy$ inatoa gharama, kwa dola, ya kuzalisha chombo mstatili ambao juu na chini ni mraba na upande x miguu na pande za urefu y miguu. Pata gharama ya kuzalisha sanduku yenye futi x=6 na y=futi 4.

Jibu

$576

Mfano$\PageIndex{44}$

Polynomial$6x^{2}+15xy$ inatoa gharama, kwa dola, ya kuzalisha chombo mstatili ambao juu na chini ni mraba na upande x miguu na pande za urefu y miguu. Pata gharama ya kuzalisha sanduku yenye futi x=5 na y=futi 8.

Jibu

$750

Dhana muhimu

• Monomials
  • Monomial ni neno la fomu$ax^{m}$, ambapo aa ni mara kwa mara na mm ni namba nzima
    
• Polynomials
  • polynomial -monomial, au monomials mbili au zaidi pamoja na kuongeza au kutoa ni polynomial.
  • monomial -polynomial na neno moja hasa inaitwa monomial.
  • binomial —polynomial yenye maneno mawili hasa inaitwa binomial.
  • trinomial -polynomial na maneno matatu hasa inaitwa trinomial.
    
• Shahada ya Polynomial
  • Kiwango cha neno ni jumla ya watazamaji wa vigezo vyake.
  • Kiwango cha mara kwa mara ni 0.
  • Kiwango cha polynomial ni kiwango cha juu cha masharti yake yote.

faharasa

binomial

Binomial ni polynomial na maneno mawili hasa.

shahada ya mara kwa mara

Kiwango cha mara kwa mara yoyote ni 0.

shahada ya polynomial

Kiwango cha polynomial ni kiwango cha juu cha masharti yake yote.

shahada ya muda

Kiwango cha neno ni kielelezo cha kutofautiana kwake.

monomial

Monomial ni neno la fomu$ax^m$, ambapo a ni mara kwa mara na m ni namba nzima; monomial ina muda mmoja hasa.

polynomial

Polynomial ni monomial, au monomials mbili au zaidi pamoja na kuongeza au kuondoa.

fomu ya kawaida

Polynomial iko katika fomu ya kawaida wakati maneno ya polynomial yameandikwa katika utaratibu wa kushuka kwa digrii.

ya trinomial

Trinomial ni polynomial na maneno matatu hasa.