Skip to main content
Global

5.6E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    177379

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Tambua Iwapo Jozi iliyoamriwa ni Suluhisho la Mfumo wa Usawa wa Mstari

    Katika mazoezi yafuatayo, onyesha kama kila jozi iliyoamriwa ni suluhisho la mfumo.

    Zoezi\(\PageIndex{1}\)

    \(\left\{\begin{array}{l}{3 x+y>5} \\ {2 x-y \leq 10}\end{array}\right.\)

    1. (3, 1-3)
    2. (7,1)
    Jibu
    1. kweli
    2. uwongo
    Zoezi\(\PageIndex{2}\)

    \(\left\{\begin{array}{l}{4 x-y<10} \\ {-2 x+2 y>-8}\end{array}\right.\)

    1. (5,-2)
    2. (-1,3)
    Zoezi\(\PageIndex{3}\)

    \(\left\{\begin{array}{l}{y>\frac{2}{3} x-5} \\ {x+\frac{1}{2} y \leq 4}\end{array}\right.\)

    1. (6, -4)
    2. (3,0)
    Jibu
    1. uwongo
    2. kweli
    Zoezi\(\PageIndex{4}\)

    \(\left\{\begin{array}{l}{y<\frac{3}{2} x+3} \\ {\frac{3}{4} x-2 y<5}\end{array}\right.\)

    1. (-4, -1)
    2. (8,3)
    Zoezi\(\PageIndex{5}\)

    \(\left\{\begin{array}{l}{7 x+2 y>14} \\ {5 x-y \leq 8}\end{array}\right.\)

    1. (2,3)
    2. (7, -1)
    Jibu
    1. kweli

    uwongo

    Zoezi\(\PageIndex{6}\)

    \(\left\{\begin{array}{l}{6 x-5 y<20} \\ {-2 x+7 y>-8}\end{array}\right.\)

    1. (1, 1-3)
    2. (-4,4)
    Zoezi\(\PageIndex{7}\)

    \(\left\{\begin{array}{l}{2 x+3 y \geq 2} \\ {4 x-6 y<-1}\end{array}\right.\)

    1. \(\left(\frac{3}{2}, \frac{4}{3}\right)\)
    2. \(\left(\frac{1}{4}, \frac{7}{6}\right)\)
    Jibu
    1. kweli
    2. kweli
    Zoezi\(\PageIndex{8}\)

    \(\left\{\begin{array}{l}{5 x-3 y<-2} \\ {10 x+6 y>4}\end{array}\right.\)

    1. \(\left(\frac{1}{5}, \frac{2}{3}\right)\)
    2. \(\left(-\frac{3}{10}, \frac{7}{6}\right)\)

    Tatua Mfumo wa Usawa wa Linear kwa Graphing

    Katika mazoezi yafuatayo, tatua kila mfumo kwa kuchora.

    Zoezi\(\PageIndex{9}\)

    \(\left\{\begin{array}{l}{y \leq 3 x+2} \\ {y>x-1}\end{array}\right.\)

    Jibu

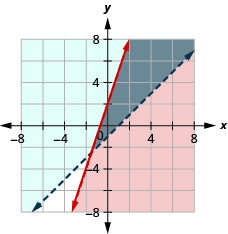
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya y ni chini ya au sawa na 3x + 2 na y ni kubwa kuliko x — 1. Eneo upande wa kushoto au kulia wa kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limevua rangi tofauti. Mstari wote ni dotted.

    Zoezi\(\PageIndex{10}\)

    \(\left\{\begin{array}{l}{y<-2 x+2} \\ {y \geq-x-1}\end{array}\right.\)

    Zoezi\(\PageIndex{11}\)

    \(\left\{\begin{array}{l}{y<2 x-1} \\ {y \leq-\frac{1}{2} x+4}\end{array}\right.\)

    Jibu

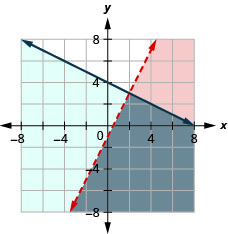
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu y y ni chini ya 2x - 1 na y ni chini ya au sawa na - (1/2) x + 4. Eneo upande wa kushoto au chini ya kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limefunika rangi tofauti. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{12}\)

    \(\left\{\begin{array}{l}{y \geq-\frac{2}{3} x+2} \\ {y>2 x-3}\end{array}\right.\)

    Zoezi\(\PageIndex{13}\)

    \(\left\{\begin{array}{l}{x-y>1} \\ {y<-\frac{1}{4} x+3}\end{array}\right.\)

    Jibu

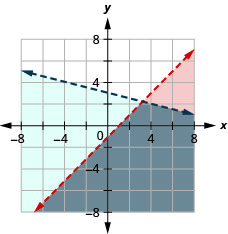
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya x — y ni kubwa kuliko 1 na y ni chini ya — (1/4) x + 3. Eneo la kulia au chini ya kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti. Mstari wote ni dotted.

    Zoezi\(\PageIndex{14}\)

    \(\left\{\begin{array}{l}{x+2 y<4} \\ {y<x-2}\end{array}\right.\)

    Zoezi\(\PageIndex{15}\)

    \(\left\{\begin{array}{l}{3 x-y \leq 6} \\ {y \geq-\frac{1}{2} x}\end{array}\right.\)

    Jibu

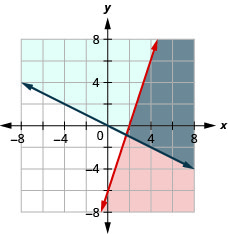
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya 3x — y ni chini ya au sawa na 6 na y ni kubwa kuliko au sawa na — (1/2) x. eneo la kulia au juu ya kila mstari ni kivuli rangi tofauti na eneo mwingiliano pia kivuli rangi tofauti.

    Zoezi\(\PageIndex{16}\)

    \(\left\{\begin{array}{l}{2 x+4 y \geq 8} \\ {y \leq \frac{3}{4} x}\end{array}\right.\)

    Zoezi\(\PageIndex{17}\)

    \(\left\{\begin{array}{l}{2 x-5 y<10} \\ {3 x+4 y \geq 12}\end{array}\right.\)

    Jibu

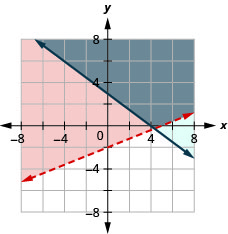
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya 2x — 5y ni chini ya 10 na 3x +4y ni kubwa kuliko au sawa na 12. Eneo la kulia juu ya kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{18}\)

    \(\left\{\begin{array}{l}{3 x-2 y \leq 6} \\ {-4 x-2 y>8}\end{array}\right.\)

    Zoezi\(\PageIndex{19}\)

    \(\left\{\begin{array}{l}{2 x+2 y>-4} \\ {-x+3 y \geq 9}\end{array}\right.\)

    Jibu

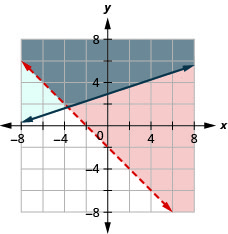
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 2x + 2y ni kubwa kuliko -4 na -x + 3y ni kubwa kuliko au sawa na 9. Eneo la kulia au juu ya kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{20}\)

    \(\left\{\begin{array}{l}{2 x+y>-6} \\ {-x+2 y \geq-4}\end{array}\right.\)

    Zoezi\(\PageIndex{21}\)

    \(\left\{\begin{array}{l}{x-2 y<3} \\ {y \leq 1}\end{array}\right.\)

    Jibu

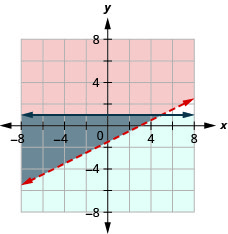
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya x — 2y ni chini ya 3 na y ni chini ya au sawa na 1. Eneo upande wa kushoto au chini ya kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limefunika rangi tofauti. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{22}\)

    \(\left\{\begin{array}{l}{x-3 y>4} \\ {y \leq-1}\end{array}\right.\)

    Zoezi\(\PageIndex{23}\)

    \(\left\{\begin{array}{l}{y \geq-\frac{1}{2} x-3} \\ {x \leq 2}\end{array}\right.\)

    Jibu

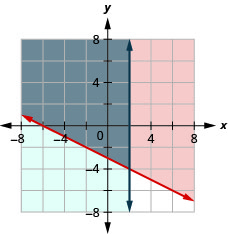
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya y y ni kubwa kuliko au sawa na (-1/2) x - 3 na x ni chini ya au sawa na 2. Eneo upande wa kushoto au kulia wa kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limevua rangi tofauti.

    Zoezi\(\PageIndex{24}\)

    \(\left\{\begin{array}{l}{y \leq-\frac{2}{3} x+5} \\ {x \geq 3}\end{array}\right.\)

    Zoezi\(\PageIndex{25}\)

    \(\left\{\begin{array}{l}{y \geq \frac{3}{4} x-2} \\ {y<2}\end{array}\right.\)

    Jibu

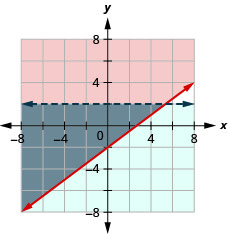
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya y y ni kubwa kuliko au sawa na (3/4) x - 2 na y ni chini ya 2. Eneo upande wa kushoto au chini ya kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limefunika rangi tofauti. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{26}\)

    \(\left\{\begin{array}{l}{y \leq-\frac{1}{2} x+3} \\ {y<1}\end{array}\right.\)

    Zoezi\(\PageIndex{27}\)

    \(\left\{\begin{array}{l}{3 x-4 y<8} \\ {x<1}\end{array}\right.\)

    Jibu

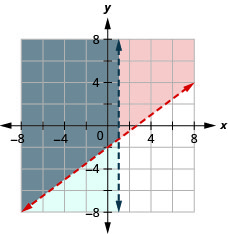
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya 3x — 4y ni chini ya 8 na x ni chini ya 1. Eneo upande wa kushoto wa kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limevua rangi tofauti. Mstari wote ni dotted.

    Zoezi\(\PageIndex{28}\)

    \(\left\{\begin{array}{l}{-3 x+5 y>10} \\ {x>-1}\end{array}\right.\)

    Zoezi\(\PageIndex{29}\)

    \(\left\{\begin{array}{l}{x \geq 3} \\ {y \leq 2}\end{array}\right.\)

    Jibu

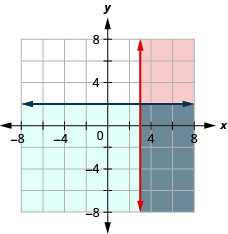
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya x ni kubwa kuliko au sawa na 3 na y chini ya au sawa na 2. Eneo la kulia au chini ya kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti.

    Zoezi\(\PageIndex{30}\)

    \(\left\{\begin{array}{l}{x \leq-1} \\ {y \geq 3}\end{array}\right.\)

    Zoezi\(\PageIndex{31}\)

    \(\left\{\begin{array}{l}{2 x+4 y>4} \\ {y \leq-\frac{1}{2} x-2}\end{array}\right.\)

    Jibu

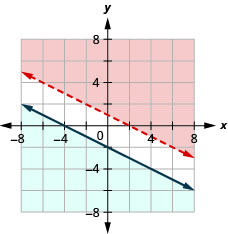
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 2x + 4y ni kubwa kuliko 4 na y ni chini ya au sawa na (-1/2) x - 2. Eneo la kushoto au kulia la kila mstari ni kivuli rangi tofauti. Hakuna eneo ambako maeneo ya kivuli yanaingiliana. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{32}\)

    \(\left\{\begin{array}{l}{x-3 y \geq 6} \\ {y>\frac{1}{3} x+1}\end{array}\right.\)

    Zoezi\(\PageIndex{33}\)

    \(\left\{\begin{array}{l}{-2 x+6 y<0} \\ {6 y>2 x+4}\end{array}\right.\)

    Jibu

    Hakuna ufumbuzi

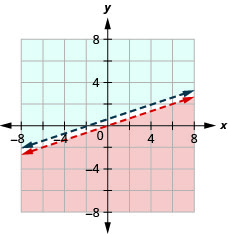
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y -2x + 6y ni chini ya 0 na 6y ni kubwa kuliko 2x + 4. Eneo la kushoto au kulia la kila mstari ni kivuli rangi tofauti. Hakuna eneo ambako maeneo ya kivuli yanaingiliana. Mstari wote ni dotted.

    Zoezi\(\PageIndex{34}\)

    \(\left\{\begin{array}{l}{-3 x+6 y>12} \\ {4 y \leq 2 x-4}\end{array}\right.\)

    Zoezi\(\PageIndex{35}\)

    \(\left\{\begin{array}{l}{y \geq-3 x+2} \\ {3 x+y>5}\end{array}\right.\)

    Jibu

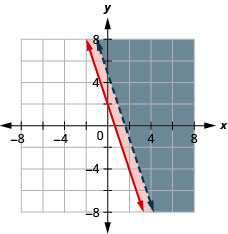
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya y y ni kubwa kuliko au sawa na -3x + 2 na 3x + y ni kubwa kuliko 5. Eneo la kulia la kila mstari ni kivuli rangi tofauti. Mstari mmoja ni ndani ya eneo la kivuli la nyingine. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{36}\)

    \(\left\{\begin{array}{l}{y \geq \frac{1}{2} x-1} \\ {-2 x+4 y \geq 4}\end{array}\right.\)

    Zoezi\(\PageIndex{37}\)

    \(\left\{\begin{array}{l}{y \leq-\frac{1}{4} x-2} \\ {x+4 y<6}\end{array}\right.\)

    Jibu

    x+4y<6

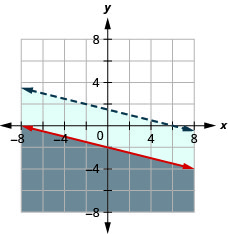
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya y ni chini ya au sawa na (hasi 1/4) x — 2 na x + 4y ni chini ya 6. Eneo chini ya kila mstari ni kivuli rangi tofauti. Mstari mmoja ni ndani ya eneo la kivuli la nyingine. Mstari mmoja umewekwa.

    Zoezi\(\PageIndex{38}\)

    \(\left\{\begin{array}{l}{y \geq 3 x-1} \\ {-3 x+y>-4}\end{array}\right.\)

    Zoezi\(\PageIndex{39}\)

    \(\left\{\begin{array}{l}{3 y>x+2} \\ {-2 x+6 y>8}\end{array}\right.\)

    Jibu

    \(-2 x+6 y>8\)

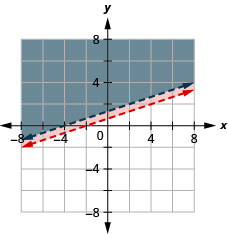
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 3y ni kubwa kuliko x + 2 na -2x + 6y ni kubwa kuliko 8. Eneo la juu ya kila mstari ni kivuli rangi tofauti. Mstari mmoja ni ndani ya eneo la kivuli la nyingine. Mstari wote ni dotted.

    Zoezi\(\PageIndex{40}\)

    \(\left\{\begin{array}{l}{y<\frac{3}{4} x-2} \\ {-3 x+4 y<7}\end{array}\right.\)

    Kutatua Matumizi ya Mifumo ya Usawa

    Katika mazoezi yafuatayo, tafsiri kwa mfumo wa kutofautiana na kutatua.

    Zoezi\(\PageIndex{41}\)

    Caitlyn anauza michoro yake katika haki ya kata. Anataka kuuza angalau michoro 60 na ana picha na mandhari. Yeye anauza portraits kwa $15 na mandhari kwa $10. Anahitaji kuuza angalau $800 yenye thamani ya michoro ili kupata faida.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, atafanya faida ikiwa anauza picha 20 na mandhari ya 35?
    4. Je, atafanya faida ikiwa anauza picha za 50 na mandhari ya 20?
    Jibu
    1. \(\left\{\begin{array}{l}{p+l \geq 60} \\ {15 p+10 l \geq 800}\end{array}\right.\)

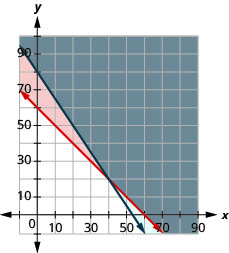
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya p + l ni kubwa kuliko au sawa na 60 na 15p + 10l ni kubwa kuliko au sawa na 800. Eneo upande wa kushoto wa kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limevua rangi tofauti.

    3. Hapana

    4. Ndio

    Zoezi\(\PageIndex{42}\)

    Jake hataki kutumia zaidi ya $50 kwenye mifuko ya mbolea na peat moss kwa bustani yake. Mbolea gharama $2 mfuko na Peat moss gharama $5 mfuko. Van Jake anaweza kushikilia katika zaidi 20 mifuko.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, anaweza kununua mifuko 15 ya mbolea na mifuko 4 ya peat moss?
    4. Je, anaweza kununua mifuko 10 ya mbolea na mifuko 10 ya peat moss?
    Zoezi\(\PageIndex{43}\)

    Reiko anahitaji barua kadi zake za Krismasi na vifurushi na anataka kuweka gharama zake za barua pepe kwa si zaidi ya $500. Idadi ya kadi ni angalau 4 zaidi ya mara mbili idadi ya vifurushi. Gharama ya barua pepe kadi (na picha iliyoambatanishwa) ni $3 na kwa mfuko gharama ni $7.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, yeye barua 60 kadi na 26 paket?
    4. Je, yeye barua 90 kadi na 40 paket?
    Jibu
    1. \(\left\{\begin{array}{l}{7 p+3 c \leq 500} \\ {p \geq 2 c+4}\end{array}\right.\)

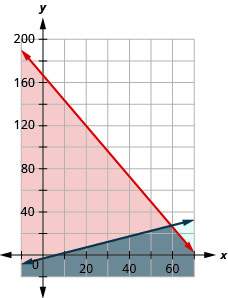
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 7p + 3c ni chini ya au sawa na 500 na p ni kubwa kuliko au sawa na 2c + 4. Eneo upande wa kushoto au chini ya kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limefunika rangi tofauti.

    3. Ndio

    4. Hapana

    Zoezi\(\PageIndex{44}\)

    Juan anasoma kwa ajili ya mitihani yake ya mwisho katika Kemia na Algebra. Anajua ana masaa 24 tu ya kujifunza, na itachukua angalau mara tatu kwa muda mrefu kujifunza kwa Algebra kuliko Kemia.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, anaweza kutumia masaa 4 kwenye Kemia na masaa 20 kwenye Algebra?
    4. Je, anaweza kutumia masaa 6 kwenye Kemia na masaa 18 kwenye Algebra?
    Zoezi\(\PageIndex{45}\)

    Jocelyn ni mjamzito na anahitaji kula angalau kalori 500 zaidi kwa siku kuliko kawaida. Wakati wa kununua mboga siku moja na bajeti ya $15 kwa ajili ya chakula cha ziada, yeye hununua ndizi ambazo zina kalori 90 kila mmoja na chokoleti granola baa ambazo zina kalori 150 kila mmoja. Ndizi ziligharimu $0.35 kila mmoja na baa za granola zina gharama $2.50 kila mmoja.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, angeweza kununua ndizi 5 na baa 6 za granola?
    4. Je, angeweza kununua ndizi 3 na baa 4 za granola?
    Jibu
    1. \(\left\{\begin{array}{l}{90 b+150 g \geq 500} \\ {0.35 b+2.50 g \leq 15}\end{array}\right.\)

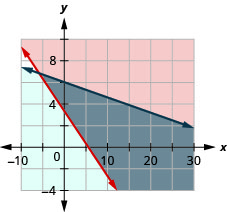
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu x y ya 90b + 150g ni kubwa kuliko au sawa na 500 na 0.35b + 2.50g ni chini ya au sawa na 15. Eneo la kulia au chini ya kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti.

    3. Hapana

    4. Ndio

    Zoezi\(\PageIndex{46}\)

    Mark ni kujaribu kujenga misuli molekuli na hivyo anahitaji kula angalau gramu 80 za ziada za protini kwa siku. Chupa ya maji ya protini inachukua $3.20 na bar ya protini ina gharama $1.75. Maji ya protini hutoa gramu 27 za protini na vifaa vya bar 16 gramu. Kama ana $10 dola kwa kutumia

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, angeweza kununua chupa 3 za maji ya protini na bar 1 ya protini?
    4. Hakuweza kununua chupa za maji ya protini na baa 5 za protini?
    Zoezi\(\PageIndex{47}\)

    Jocelyn anataka kuongeza matumizi yake ya protini na ulaji wa kalori. Anataka kuwa na angalau gramu 35 za protini kila siku na si zaidi ya kalori 200 za ziada kila siku. Ounce ya jibini la cheddar ina gramu 7 za protini na kalori 110. Ounce ya jibini la parmesan ina gramu 11 za protini na kalori 22.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, anaweza kula ounce 1 ya jibini la cheddar na ounces 3 ya jibini la parmesan?
    4. Je, anaweza kula ounces 2 ya jibini la cheddar na 1 ounce ya jibini la parmesan?
    Jibu
    1. \(\left\{\begin{array}{l}{7 c+11 p \geq 35} \\ {110 c+22 p \leq 200}\end{array}\right.\)

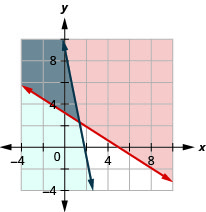
    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 7c + 11p ni kubwa kuliko au sawa na 35 na 110c + 22p ni chini ya au sawa na 200. Eneo upande wa kushoto au kulia wa kila mstari ni kivuli rangi tofauti na eneo la kuingiliana pia limevua rangi tofauti.

    3. Ndio

    4. Hapana

    Zoezi\(\PageIndex{48}\)

    Mark anaongeza zoezi lake la kawaida kwa kukimbia na kutembea angalau maili 4 kila siku. Lengo lake ni kuchoma kiwango cha chini cha kalori 1,500 kutoka kwa zoezi hili. Kutembea kuchoma kalori 270/maili na kukimbia kuchoma kalori 650.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, angeweza kufikia lengo lake kwa kutembea maili 3 na kukimbia maili 1?
    4. Je, angeweza kufikia lengo lake kwa kutembea maili 2 na kukimbia maili 2?

    kila siku Math

    Zoezi\(\PageIndex{49}\)

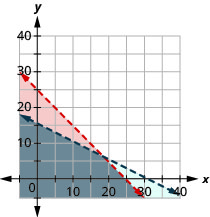
    Tiketi za mchezo wa Ligi ya Baseball ya Marekani kwa watu wazima 3 na watoto 3 zina gharama chini ya $75, wakati tiketi za watu wazima 2 na watoto 4 zina gharama chini ya $62.

    1. Andika mfumo wa kutofautiana kwa mfano wa tatizo hili.
    2. Graph mfumo.
    3. Je, tiketi zinaweza gharama $20 kwa watu wazima na $8 kwa watoto?
    4. Je, tiketi zinaweza gharama $15 kwa watu wazima na $5 kwa watoto?
    Jibu
    1. \ (\ kushoto\ {\ kuanza {safu} {l} {3 a+3 c<75}\\ {2 a+4 c<62}\ mwisho {safu}\ haki. \

    Takwimu hii inaonyesha grafu kwenye ndege ya kuratibu ya x y ya 3a + 3c ni chini ya 75 na 2a + 4c ni chini ya 62. Eneo upande wa kushoto wa kila mstari ni kivuli rangi tofauti na eneo linaloingiliana pia limefunika rangi tofauti. Mstari wote ni dotted.

    3. Hapana

    4. Ndio

    Zoezi\(\PageIndex{50}\)

    Babu na Grandma wanawatendea familia zao kwenye sinema. Tiketi za matinee zina gharama $4 kwa mtoto na $4 kwa kila mtu mzima. Tiketi za jioni zina gharama $6 kwa mtoto na $8 kwa mtu mzima. Wanapanga kutumia zaidi ya $80 kwenye tiketi za matinee na si zaidi ya $100 kwenye tiketi za jioni.

    1. Andika mfumo wa kutofautiana kwa mfano wa hali hii.
    2. Graph mfumo.
    3. Je, wanaweza kuchukua watoto 9 na watu wazima 4 kwa maonyesho yote?
    4. Wangeweza kuchukua watoto 8 na watu wazima wa 5 kwa maonyesho yote mawili?

    Mazoezi ya kuandika

    Zoezi\(\PageIndex{51}\)

    Grafu usawa\(x-y \geq 3 .\) Unajuaje upande gani wa mstari\(x-y=3\) unapaswa kuwa kivuli?

    Jibu

    Majibu yatatofautiana.

    Zoezi\(\PageIndex{52}\)

    Grafu mfumo\(\left\{\begin{array}{l}{x+2 y \leq 6} \\ {y \geq-\frac{1}{2} x-4}\end{array}\right. .\) Je! Suluhisho linamaanisha nini?

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    Jedwali hili lina safu nne na safu nne. Nguzo zimeandikwa, “Ninaweza...,” “kwa ujasiri.” “kwa msaada fulani.” “Hapana — Siipati!” Safu pekee zilizojaa ni chini ya safu ya “Naweza...”. Safu zinasema, “onyesha kama jozi iliyoamriwa ni suluhisho la mfumo wa kutofautiana kwa mstari.” “Tatua mfumo wa kutofautiana kwa mstari kwa kuchora picha.” na “kutatua matumizi ya mifumo ya kutofautiana.”

    b Baada ya kuchunguza orodha hii, utafanya nini ili uwe na ujasiri kwa malengo yote?