5.1E: Mazoezi
- Page ID
- 177409
Mazoezi hufanya kamili
Kuamua Kama Jozi Amri ni Suluhisho la Mfumo wa Equations. Katika mazoezi yafuatayo, onyesha kama pointi zifuatazo ni ufumbuzi wa mfumo uliopewa wa equations.
\(\begin{cases}{2x−6y=0} \\ {3x−4y=5}\end{cases}\)
- (3,1)
- (-3,4)
- Jibu
-
- ndiyo
- hapana
\(\begin{cases}{7x-4y=-1} \\ {-3x-2y = 1} \end{cases}\)
- (\(-\frac{3}{13}\),\(-\frac{2}{13}\))
- (1, -2)
- Jibu
-
- ndiyo
- hapana
\(\left\{\begin{array}{l}{2 x+y=5} \\ {x+y=1}\end{array}\right.\)
- (4, 1-3)
- (2,0)
- Jibu
-
- ndiyo
- hapana
\(\left\{\begin{array}{l}{-3 x+y=8} \\ {-x+2 y=-9}\end{array}\right.\)
- (-5, -7)
- (-5,7)
\(\left\{\begin{array}{l}{x+y=2} \\ {y=\frac{3}{4} x}\end{array}\right.\)
- \(\left(\frac{8}{7}, \frac{6}{7}\right)\)
- \(\left(1, \frac{3}{4}\right)\)
- Jibu
-
- ndiyo
- hapana
\(\left\{\begin{array}{l}{x+y=1} \\ {y=\frac{2}{5} x}\end{array}\right.\)
- \(\left(\frac{5}{7}, \frac{2}{7}\right)\)
- (5,2)
\(\left\{\begin{array}{l}{x+5 y=10} \\ {y=\frac{3}{5} x+1}\end{array}\right.\)
- (-10,4)
- \(\left(\frac{5}{4}, \frac{7}{4}\right)\)
- Jibu
-
- hapana
- ndiyo
\(\left\{\begin{array}{l}{x+3 y=9} \\ {y=\frac{2}{3} x-2}\end{array}\right.\)
- (-6,5)
- \(\left(5, \frac{4}{3}\right)\)
Kutatua Mfumo wa Equations Linear na Graphing Katika mazoezi yafuatayo, kutatua mifumo yafuatayo ya equations kwa graphing.
\(\left\{\begin{array}{l}{3 x+y=-3} \\ {2 x+3 y=5}\end{array}\right.\)
- Jibu
-
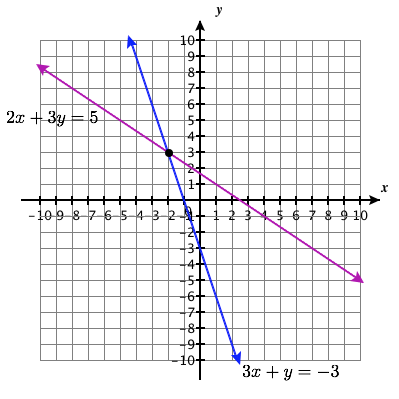
Ufumbuzi Point:\((-2,3)\)
\(\left\{\begin{array}{l}{-x+y=2} \\ {2 x+y=-4}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.\)
- Jibu
-
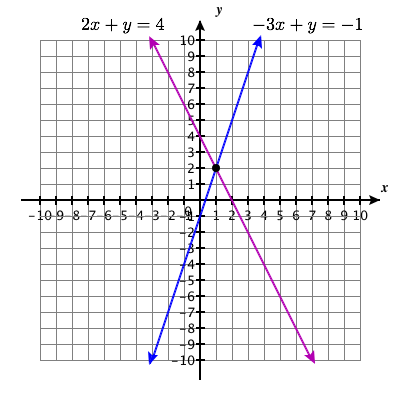
Ufumbuzi Point:\((1,2)\)
\(\left\{\begin{array}{l}{-2 x+3 y=-3} \\ {x+y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=x+2} \\ {y=-2 x+2}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((0,2)\)
\(\left\{\begin{array}{l}{y=x-2} \\ {y=-3 x+2}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=\frac{3}{2} x+1} \\ {y=-\frac{1}{2} x+5}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((2,4)\)
\(\left\{\begin{array}{l}{y=\frac{2}{3} x-2} \\ {y=-\frac{1}{3} x-5}\end{array}\right.\)
\(\left\{\begin{array}{l}{-x+y=-3} \\ {4 x+4 y=4}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((2,-1)\)
\(\left\{\begin{array}{l}{x-y=3} \\ {2 x-y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+y=-1} \\ {2 x+y=4}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((1,2)\)
\(\left\{\begin{array}{l}{-3 x+y=-2} \\ {4 x-2 y=6}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=5} \\ {2 x-y=4}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((3,2)\)
\(\left\{\begin{array}{l}{x-y=2} \\ {2 x-y=6}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=2} \\ {x-y=0}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((1,1)\)
\(\left\{\begin{array}{l}{x+y=6} \\ {x-y=-8}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-5} \\ {x-y=3}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((-1,-4)\)
\(\left\{\begin{array}{l}{x+y=4} \\ {x-y=0}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+y=-4} \\ {-x+2 y=-2}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((3,3)\)
\(\left\{\begin{array}{l}{-x+3 y=3} \\ {x+3 y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{-2 x+3 y=3} \\ {x+3 y=12}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((-5,6)\)
\(\left\{\begin{array}{l}{2 x-y=4} \\ {2 x+3 y=12}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x+3 y=6} \\ {y=-2}\end{array}\right.\)
- Jibu
-
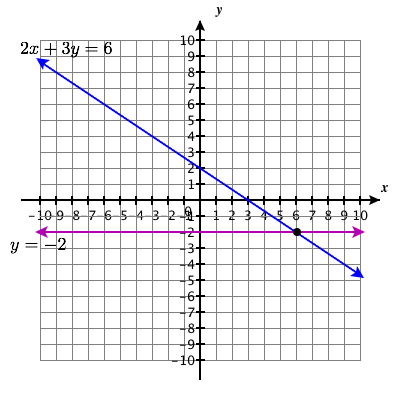
Ufumbuzi Point:\((6,−2)\)
\(\left\{\begin{array}{l}{-2 x+y=2} \\ {y=4}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-3 y=-3} \\ {y=2}\end{array}\right.\)
Jibu
-
Ufumbuzi Point:\((3,2)\)
\(\left\{\begin{array}{l}{2 x-2 y=8} \\ {y=-3}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x-y=-1} \\ {x=1}\end{array}\right.\)
- Jibu
-
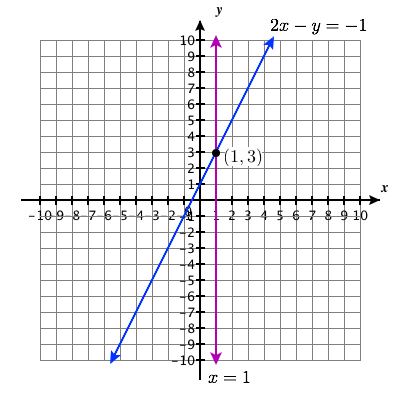
Ufumbuzi Point:\((1,3)\)
\(\left\{\begin{array}{l}{x+2 y=2} \\ {x=-2}\end{array}\right.\)
\(\left\{\begin{array}{l}{x-3 y=-6} \\ {x=-3}\end{array}\right.\)
- Jibu
-
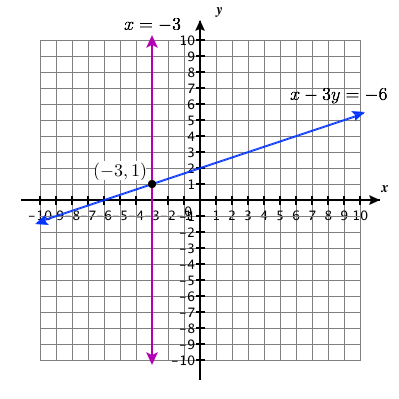
Ufumbuzi Point:\((−3,1)\)
\(\left\{\begin{array}{l}{x+y=4} \\ {x=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x-3 y=8} \\ {8 x-6 y=14}\end{array}\right.\)
- Jibu
-
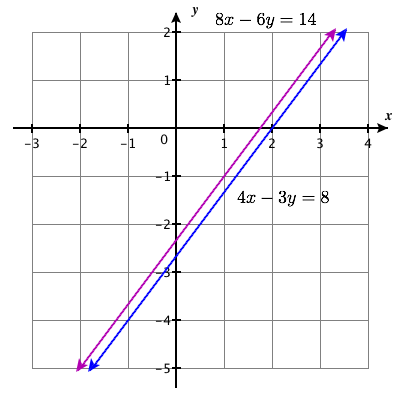
hakuna suluhisho
\(\left\{\begin{array}{l}{x+3 y=4} \\ {-2 x-6 y=3}\end{array}\right.\)
\(\left\{\begin{array}{l}{-2 x+4 y=4} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Jibu
-
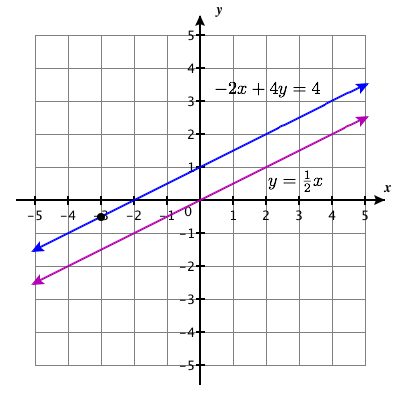
hakuna suluhisho
\(\left\{\begin{array}{l}{3 x+5 y=10} \\ {y=-\frac{3}{5} x+1}\end{array}\right.\)
\(\left\{\begin{array}{l}{x=-3 y+4} \\ {2 x+6 y=8}\end{array}\right.\)
- Jibu
-
hakuna suluhisho
\(\left\{\begin{array}{l}{4 x=3 y+7} \\ {8 x-6 y=14}\end{array}\right.\)
\(\left\{\begin{array}{l}{2 x+y=6} \\ {-8 x-4 y=-24}\end{array}\right.\)
- Jibu
-
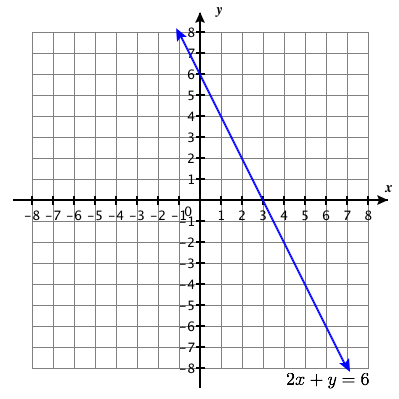
ufumbuzi mkubwa sana na kuweka ufumbuzi:\(\big\{ (x,y) | 2 x+y=6\big\}\)
\(\left\{\begin{array}{l}{5 x+2 y=7} \\ {-10 x-4 y=-14}\end{array}\right.\)
\(\left\{\begin{array}{l}{x+3 y=-6} \\ {4 y=-\frac{4}{3} x-8}\end{array}\right.\)
- Jibu
-
ufumbuzi mkubwa sana na kuweka ufumbuzi:\(\big\{ (x,y) | x+3 y=-6\big\}\)
\(\left\{\begin{array}{l}{-x+2 y=-6} \\ {y=-\frac{1}{2} x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{-3 x+2 y=-2} \\ {y=-x+4}\end{array}\right.\)
- Jibu
-
Ufumbuzi Point:\((2,2)\)
\(\left\{\begin{array}{l}{-x+2 y=-2} \\ {y=-x-1}\end{array}\right.\)
Kuamua Idadi ya Ufumbuzi wa Mfumo wa Linear Bila kuchora mifumo ifuatayo ya equations, kuamua idadi ya ufumbuzi na kisha uainishe mfumo wa equations.
\(\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {-2 x+3 y=5}\end{array}\right.\)
- Jibu
-
0 ufumbuzi
\(\left\{\begin{array}{l}{y=\frac{1}{3} x+2} \\ {x-3 y=9}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-2 x+1} \\ {4 x+2 y=8}\end{array}\right.\)
- Jibu
-
0 ufumbuzi
\(\left\{\begin{array}{l}{y=3 x+4} \\ {9 x-3 y=18}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=\frac{2}{3} x+1} \\ {2 x-3 y=7}\end{array}\right.\)
- Jibu
-
0 ufumbuzi
\(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=-3 x-1}\end{array}\right.\)
\(\left\{\begin{array}{l}{4 x+2 y=10} \\ {4 x-2 y=-6}\end{array}\right.\)
- Jibu
-
thabiti, 1 ufumbuzi
\(\left\{\begin{array}{l}{5 x+3 y=4} \\ {2 x-3 y=5}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=-\frac{1}{2} x+5} \\ {x+2 y=10}\end{array}\right.\)
- Jibu
-
ufumbuzi mkubwa sana
\(\left\{\begin{array}{l}{y=x+1} \\ {-x+y=1}\end{array}\right.\)
\(\left\{\begin{array}{l}{y=2 x+3} \\ {2 x-y=-3}\end{array}\right.\)
- Jibu
-
ufumbuzi mkubwa sana
\(\left\{\begin{array}{l}{5 x-2 y=10} \\ {y=\frac{5}{2} x-5}\end{array}\right.\)
Tatua Matumizi ya Mifumo ya Equations na Graphing Katika mazoezi yafuatayo, tatua.
Molly ni kufanya strawberry infused maji Kwa kila ounce ya juisi ya strawberry, anatumia mara tatu kama ounces nyingi za maji. Ni ounces ngapi ya juisi ya strawberry na ngapi ounces ya maji anayohitaji kufanya ounces 64 ya maji ya strawberry
- Jibu
-
Molly anahitaji ounces 16 ya juisi ya strawberry na ounces 48
Jamal anafanya mchanganyiko wa vitafunio ambao una pretzels na karanga tu. Kwa kila ounce ya karanga, atatumia ounces 2 ya pretzels. Ni ounces ngapi ya pretzels na ngapi ounces ya karanga anahitaji kufanya ounces 45 ya mchanganyiko wa vitafunio?
Enrique anafanya mchanganyiko wa chama ambao una zabibu na karanga. Kwa kila ounce ya karanga, anatumia mara mbili kiasi cha zabibu. Ni ounces ngapi ya karanga na ngapi ounces ya zabibu anahitaji kufanya ounces 24 ya mchanganyiko wa chama?
- Jibu
-
Enrique anahitaji ounces 8 za karanga na ounces 16 za maji.
Owen ni kufanya lemonade kutoka makini. Idadi ya quarts ya maji anayohitaji ni mara 4 idadi ya quarts ya makini. Ni quarts ngapi za maji na ngapi quarts ya makini Owen inahitaji kufanya quarts 100 ya lemonade?
kila siku Math
Leo anapanga bustani yake ya maua ya spring. Anataka kupanda mimea ya tulip na daffodil. Atapanda mara 6 kama balbu nyingi za daffodil kama balbu za tulip. Ikiwa anataka kupanda balbu 350, ni balbu ngapi za tuli na ngapi za daffodil zinapaswa kupanda?
- Jibu
-
Leo inapaswa kupanda tulips 50 na daffodils 300.
Kampuni ya masoko inatafiti watu 1,200. Walichunguza wanawake mara mbili kama wanaume. Walichunguza wanaume na wanawake wangapi?
Mazoezi ya kuandika
Katika mfumo wa equations linear, equations mbili zina mteremko sawa. Eleza ufumbuzi unaowezekana kwa mfumo.
- Jibu
-
Kutokana na kwamba inajulikana tu kwamba mteremko wa equations zote mbili ni sawa, kuna ama hakuna ufumbuzi (grafu ya equations ni sambamba) au wengi sana.
Katika mfumo wa equations linear, equations mbili na intercepts sawa. Eleza ufumbuzi unaowezekana kwa mfumo.
Self Check
Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
Kama wengi wa hundi yako walikuwa:
... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.
... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?
... hapana - Siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.


