5.2: Tatua Mifumo ya Equations na Kubadilisha
- Page ID
- 177325
Mwishoni mwa sehemu hii, utaweza:
- Tatua mfumo wa equations kwa kubadilisha
- Tatua matumizi ya mifumo ya equations kwa kubadilisha
Kabla ya kuanza, fanya jaribio hili la utayari.
- Rahisisha -5 (3—x).
Kama amekosa tatizo hili, kupitia Zoezi 1.10.43. - Kurahisisha 4-2 (n+5).
Kama amekosa tatizo hili, mapitio Zoezi 1.10.41. - Tatua kwa y. 8y-8=32,12y
Ikiwa umekosa tatizo hili, kagua Zoezi 2.3.22. - Tatua kwa x. 3x-9y=-3
Ikiwa umekosa tatizo hili, kagua Zoezi 2.6.22.
Kutatua mifumo ya equations linear kwa graphing ni njia nzuri ya kutazama aina ya ufumbuzi ambayo inaweza kusababisha. Hata hivyo, kuna matukio mengi ambapo kutatua mfumo kwa kuchora picha ni mbaya au isiyo sahihi. Ikiwa grafu zinaenea zaidi ya gridi ndogo na x na y wote kati ya -10 na 10, kuchora mistari inaweza kuwa mbaya. Na kama ufumbuzi wa mfumo sio integers, inaweza kuwa vigumu kusoma maadili yao kwa usahihi kutoka kwenye grafu.
Katika sehemu hii, tutasuluhisha mifumo ya equations linear kwa njia ya kubadilisha.
Tatua Mfumo wa Ulinganisho kwa Kubadilisha
Tutatumia mfumo huo tuliotumia kwanza kwa kuchora picha.
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
Sisi kwanza kutatua moja ya equations kwa aidha x au y. Tunaweza kuchagua ama equation na kutatua kwa aidha variable-lakini tutaweza kujaribu kufanya uchaguzi kwamba kushika kazi rahisi.
Kisha sisi badala kwamba kujieleza katika equation nyingine. Matokeo yake ni equation na tofauti moja tu-na tunajua jinsi ya kutatua wale!
Baada ya kupata thamani ya variable moja, sisi badala kwamba thamani katika moja ya equations awali na kutatua kwa variable nyingine. Hatimaye, sisi kuangalia ufumbuzi wetu na kuhakikisha inafanya equations wote kweli.
Tutaweza kujaza hatua hizi zote sasa katika Zoezi\(\PageIndex{1}\).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- Jibu
-






Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- Jibu
-
(6,1)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- Jibu
-
(4,2)
- Kutatua moja ya milinganyo kwa variable ama.
- Badilisha usemi kutoka Hatua ya 1 katika equation nyingine.
- Tatua equation inayosababisha.
- Badilisha ufumbuzi katika Hatua ya 3 katika moja ya milinganyo ya awali ili kupata variable nyingine.
- Andika suluhisho kama jozi iliyoamriwa.
- Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.
Ikiwa moja ya milinganyo katika mfumo imetolewa katika fomu ya mteremka-intercept, Hatua ya 1 tayari imefanywa! Tutaona hii katika Zoezi\(\PageIndex{4}\).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- Jibu
-
Equation ya pili tayari kutatuliwa kwa y. Sisi badala ya kujieleza katika nafasi ya y katika equation kwanza.
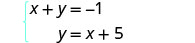
Equation ya pili tayari kutatuliwa kwa y.
Sisi badala katika equation kwanza.Badilisha nafasi ya y na x + 5. 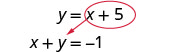
Kutatua equation kusababisha kwa x. 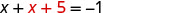
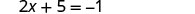
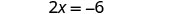
Mbadala x = -3 katika y = x + 5 ili kupata y. 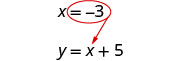
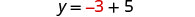
Jozi iliyoamriwa ni (-3, 2). 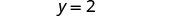
Angalia jozi iliyoamriwa katika equations zote mbili:
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)Suluhisho ni (-3, 2).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- Jibu
-
(2,4)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- Jibu
-
(-1, 1-3)
Kama equations ni kutolewa katika hali ya kiwango, tutaweza haja ya kuanza kwa kutatua kwa moja ya vigezo. Katika mfano huu ijayo, tutaweza kutatua equation kwanza kwa y.
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- Jibu
-
Tunahitaji kutatua equation moja kwa variable moja. Kisha sisi badala kwamba kujieleza katika equation nyingine.
Kutatua kwa y.
Mbadala katika equation nyingine.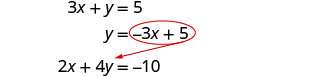
Badilisha nafasi ya y na -3 x + 5. 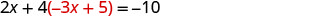
Kutatua equation kusababisha kwa x. 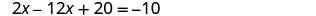
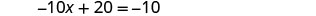
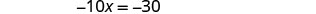
Mbadala x = 3 katika 3 x + y = 5 ili kupata y. 


Jozi iliyoamriwa ni (3, -4). 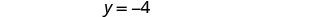
Angalia jozi iliyoamriwa katika equations zote mbili:
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)Suluhisho ni (3, -4).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- Jibu
-
(1, -2)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- Jibu
-
(2,6)
Katika Zoezi\(\PageIndex{7}\) ilikuwa rahisi kutatua kwa y katika equation ya kwanza kwa sababu ilikuwa na mgawo wa 1. Katika Zoezi\(\PageIndex{10}\) itakuwa rahisi kutatua kwa x.
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- Jibu
-
Tutatatua equation ya kwanza kwa xx na kisha kubadilisha msemo katika equation ya pili.

Kutatua kwa x.
Mbadala katika equation nyingine.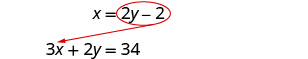
Badilisha nafasi ya x na 2 y - 2. 
Kutatua equation kusababisha kwa y. 
Mchapishaji y = 5 ndani ya x - 2 y = -1 ili kupata x.

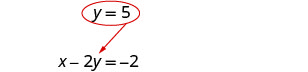



Jozi iliyoamriwa ni (8, 5). Angalia jozi iliyoamriwa katika equations zote mbili:
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)Suluhisho ni (8, 5).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- Jibu
-
(-2, -3)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- Jibu
-
(6,2)
Wakati equations zote mbili tayari kutatuliwa kwa kutofautiana sawa, ni rahisi kuchukua nafasi!
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Jibu
-
Kwa kuwa equations zote mbili zinatatuliwa kwa y, tunaweza kubadilisha moja kwa moja.
Mbadala\(\frac{1}{2}x\) kwa y katika equation ya kwanza. 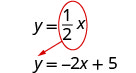
Badilisha nafasi ya y na\(\frac{1}{2}x\) 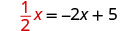
Tatua equation inayosababisha. Anza
kwa kufuta sehemu.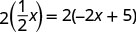
Kutatua kwa x. 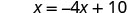
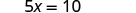
Mbadala x = 2 katika\(y = \frac{1}{2}x\) kupata y. 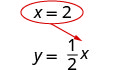
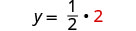
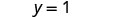
Jozi iliyoamriwa ni (2,1). Angalia jozi iliyoamriwa katika equations zote mbili:
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)Suluhisho ni (2,1).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- Jibu
-
(6,2)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- Jibu
-
(8,2)
Kuwa makini sana na ishara katika mfano unaofuata.
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- Jibu
-
Tunahitaji kutatua equation moja kwa variable moja. Tutatatua equation ya kwanza kwa y.

Tatua equation ya kwanza kwa y. 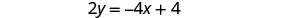
Mbadala -1 x + 2 kwa y katika equation ya pili. 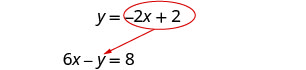
Badilisha nafasi ya y na -2 x + 2. 
Kutatua equation kwa x. 


Mbadala\(x = \frac{5}{4}\) katika 4 x + 2 y = 4 ili kupata y.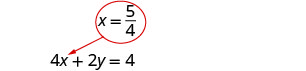



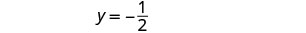
Jozi iliyoamriwa ni\((\frac{5}{4},−\frac{1}{2})\). Angalia jozi iliyoamriwa katika equations zote mbili.
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)Suluhisho ni (54, -12).
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- Jibu
-
\((2,\frac{3}{2})\)
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- Jibu
-
\((−\frac{1}{2},−2)\)
Katika Mfano, itachukua kazi kidogo zaidi kutatua equation moja kwa x au y.
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- Jibu
-
Tunahitaji kutatua equation moja kwa variable moja. Tutatatua equation ya kwanza kwa x.
Kwa kuwa 0 = 0 ni taarifa ya kweli, mfumo ni thabiti. Equations ni tegemezi. Grafu za equations hizi mbili zitatoa mstari huo. Mfumo una ufumbuzi mkubwa sana.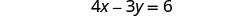
Tatua equation ya kwanza kwa x. 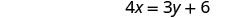
Mbadala\(\frac{3}{4} y+\frac{3}{2}\) ya x katika equation ya pili. 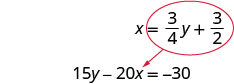
Badilisha nafasi ya x na\(\frac{3}{4} y+\frac{3}{2}\) 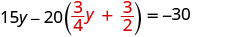
Kutatua kwa y. 

Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- Jibu
-
ufumbuzi mkubwa sana
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- Jibu
-
ufumbuzi mkubwa sana
Angalia nyuma katika equations katika Zoezi\(\PageIndex{22}\). Je, kuna njia yoyote ya kutambua kwamba wao ni mstari huo?
Hebu tuone kinachotokea katika mfano unaofuata.
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- Jibu
-
equation pili ni tayari kutatuliwa kwa y, hivyo tunaweza mbadala kwa y katika equation kwanza.
Kwa kuwa 0 = -10 ni kauli ya uongo milinganyo haipatikani. Grafu ya equation mbili itakuwa mistari sambamba. Mfumo hauna ufumbuzi.Mbadala x kwa y katika equation kwanza. 
Badilisha nafasi y na\(\frac{5}{2}x\). 
Kutatua kwa x. 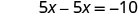

Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- Jibu
-
hakuna suluhisho
Tatua mfumo kwa kubadilisha. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- Jibu
-
hakuna suluhisho
Tatua Matumizi ya Mifumo ya Ulinganisho na Kubadilisha
Tutaweza nakala hapa mkakati wa kutatua tatizo tuliyotumia katika Kutatua Mifumo ya Equations na Graphing sehemu ya kutatua mifumo ya equations. Sasa kwa kuwa tunajua jinsi ya kutatua mifumo na badala, kwamba ni nini tutaweza kufanya katika Hatua ya 5.
- Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
- Tambua kile tunachotafuta.
- Jina kile tunachotafuta. Chagua vigezo ili kuwakilisha kiasi hicho.
- Tafsiri katika mfumo wa equations.
- Tatua mfumo wa equations kwa kutumia mbinu nzuri za algebra.
- Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
- Jibu swali kwa sentensi kamili.
Watu wengine hupata kuanzisha matatizo ya neno na vigezo viwili rahisi zaidi kuliko kuziweka na variable moja tu. Kuchagua majina ya kutofautiana ni rahisi wakati wote unahitaji kufanya ni kuandika barua mbili. Fikiria juu ya hili katika mfano ijayo - jinsi gani umefanya hivyo na variable moja tu?
Jumla ya namba mbili ni sifuri. Nambari moja ni chini ya tisa kuliko nyingine. Kupata idadi.
- Jibu
-
Hatua ya 1. Soma tatizo. Hatua ya 2. Tambua kile tunachotafuta. Tunatafuta namba mbili. Hatua ya 3. Jina kile tunachotafuta. Hebu n= namba ya kwanza
Hebu m= nambari ya piliHatua ya 4. Tafsiri katika mfumo wa equations. Jumla ya namba mbili ni sifuri. 
Nambari moja ni chini ya tisa kuliko nyingine. 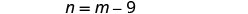
Mfumo ni: 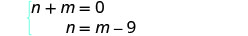
Hatua ya 5. Tatua mfumo wa
equations. Tutatumia badala
tangu equation pili ni kutatuliwa
kwa n.Mbadala m - 9 kwa n katika equation ya kwanza. 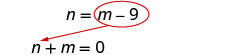
Tatua kwa m. 


Mbadala\(m=\frac{9}{2}\) katika equation pili
na kisha kutatua kwa n.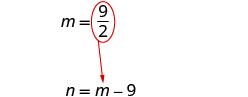
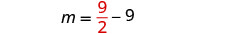
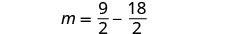
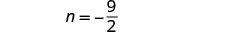
Hatua ya 6. Angalia jibu katika tatizo. Je! Nambari hizi zina maana
katika tatizo? Tutakuacha hii kwako!Hatua ya 7. Jibu swali. Idadi ni\(\frac{9}{2}\) na\(-\frac{9}{2}\).
Jumla ya namba mbili ni 10. Nambari moja ni 4 chini ya nyingine. Kupata idadi.
- Jibu
-
Idadi ni 3 na 7.
Jumla ya namba mbili ni -6. Nambari moja ni chini ya 10 kuliko nyingine. Kupata idadi.
- Jibu
-
Nambari ni 2 na -8.
Katika Zoezi\(\PageIndex{28}\), tutatumia formula kwa mzunguko wa mstatili, P = 2 L + 2 W.
Kuongeza mazoezi Nakala hapa.
- Jibu
-
Hatua ya 1. Soma tatizo. 
Hatua ya 2. Tambua unachotafuta. Tunatafuta urefu na upana. Hatua ya 3. Jina kile tunachotafuta. Hebu L= urefu
W= upanaHatua ya 4. Tafsiri katika mfumo wa equations. Mzunguko wa mstatili ni 88. 2 L + 2 W = P
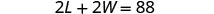
Urefu ni tano zaidi ya mara mbili upana. 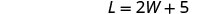
Mfumo ni: 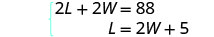
Hatua ya 5. Tatua mfumo wa equations.
Tutatumia badala tangu
equation ya pili ni kutatuliwa kwa L.
Mbadala 2 W + 5 kwa L katika equation kwanza.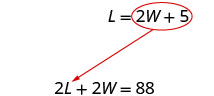
Kutatua kwa W. 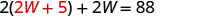
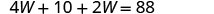
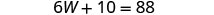
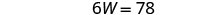
Mbadala W = 13 katika
equation ya pili na kisha kutatua kwa L.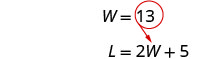
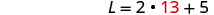
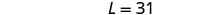
Hatua ya 6. Angalia jibu katika tatizo. Je, mstatili na urefu wa 31 na upana
13 una mzunguko wa 88? Ndiyo.Hatua ya 7. Jibu equation. Urefu ni 31 na upana ni 13.
Mzunguko wa mstatili ni 40. Urefu ni 4 zaidi ya upana. Pata urefu na upana wa mstatili.
- Jibu
-
Urefu ni 12 na upana ni 8.
Mzunguko wa mstatili ni 58. Urefu ni 5 zaidi ya mara tatu upana. Pata urefu na upana wa mstatili.
- Jibu
-
Urefu ni 23 na upana ni 6.
Kwa Zoezi\(\PageIndex{31}\) tunahitaji kukumbuka kwamba jumla ya hatua za pembe za pembetatu ni digrii 180 na kwamba pembetatu ya kulia ina angle moja ya digrii 90.
Kipimo cha moja ya pembe ndogo za pembetatu ya kulia ni kumi zaidi ya mara tatu kipimo cha angle nyingine ndogo. Pata hatua za pembe zote mbili.
- Jibu
-
Tutavuta na kuandika takwimu.
Hatua ya 1. Soma tatizo. 
Hatua ya 2. Tambua unachotafuta. Tunatafuta hatua za pembe. Hatua ya 3. Jina kile tunachotafuta. Hebu a= kipimo cha angle ya 1
b = kipimo cha angle ya 2 ndHatua ya 4. Tafsiri katika mfumo wa equations. Kipimo cha moja ya pembe ndogo
za pembetatu ya kulia ni kumi zaidi ya
mara tatu kipimo cha angle nyingine ndogo.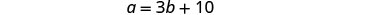
Jumla ya hatua za pembe za
pembetatu ni 180.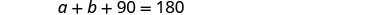
Mfumo ni: 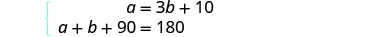
Hatua ya 5. Tatua mfumo wa equations.
Tutatumia badala tangu
equation kwanza ni kutatuliwa kwa.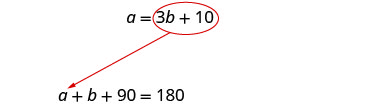
badala 3 b + 10 kwa katika equation
pili.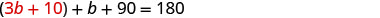
Kutatua kwa b. 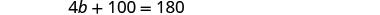


Mbadala b = 20 katika
equation kwanza na kisha kutatua kwa.

Hatua ya 6. Angalia jibu katika tatizo. Tutakuacha hii kwako! Hatua ya 7. Jibu swali. Hatua za pembe ndogo ni
20 na 70.
Kipimo cha moja ya pembe ndogo za pembetatu sahihi ni 2 zaidi ya mara 3 kipimo cha angle nyingine ndogo. Pata kipimo cha pembe zote mbili.
- Jibu
-
Kipimo cha pembe ni digrii 22 na digrii 68.
Kipimo cha moja ya pembe ndogo za pembetatu ya kulia ni 18 chini ya mara mbili kipimo cha angle nyingine ndogo. Pata kipimo cha pembe zote mbili.
- Jibu
-
Kipimo cha pembe ni digrii 36 na digrii 54.
Heather amepewa chaguzi mbili kwa mshahara wake kama mkufunzi katika mazoezi. Chaguo A ingeweza kumlipa $25,000 pamoja na $15 kwa kila kikao cha mafunzo. Chaguo B ingelipa $10,000 + $40 kwa kila kikao cha mafunzo. Ni vikao ngapi vya mafunzo vinavyofanya chaguzi za mshahara sawa?
- Jibu
-
Hatua ya 1. Soma tatizo. Hatua ya 2. Tambua unachotafuta. Tunatafuta idadi ya vikao vya mafunzo
ambayo ingeweza kulipa sawa.Hatua ya 3. Jina kile tunachotafuta. Hebu s= mshahara Heather ya.
n= idadi ya vikao vya mafunzoHatua ya 4. Tafsiri katika mfumo wa equations. Chaguo A ingeweza kumlipa $25,000 pamoja na $15
kwa kila kikao cha mafunzo.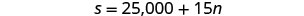
Chaguo B bila kulipa yake $10,000 + $40
kwa kila kikao cha mafunzo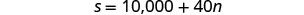
Mfumo ni: 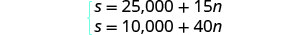
Hatua ya 5. Tatua mfumo wa equations.
Tutatumia badala.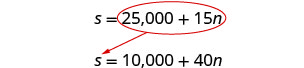
Mbadala 25,000 + 15 n kwa s katika equation ya pili. 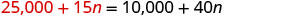
Kutatua kwa n. 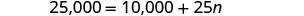
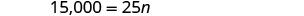

Hatua ya 6. Angalia jibu. Je, vikao vya mafunzo ya 600 kwa mwaka ni busara?
Je, chaguzi mbili ni sawa wakati n = 600?Hatua ya 7. Jibu swali. Chaguzi za mshahara itakuwa sawa kwa vikao vya mafunzo 600.
Geraldine amepewa nafasi na makampuni mawili ya bima. Kampuni ya kwanza inalipa mshahara wa $12,000 pamoja na tume ya dola 100 kwa kila sera inayouzwa. Ya pili hulipa mshahara wa $20,000 pamoja na tume ya $50 kwa kila sera iliyouzwa. Ni sera ngapi zingehitaji kuuzwa ili kulipa jumla sawa?
- Jibu
-
Kutakuwa na haja ya kuwa na sera 160 kuuzwa ili kufanya jumla ya kulipa sawa.
Kenneth sasa anauza suti kwa kampuni A kwa mshahara wa $22,000 pamoja na $10 tume kwa kila suti kuuzwa. Kampuni B inampa nafasi na mshahara wa $28,000 pamoja na tume ya $4 kwa kila suti inayouzwa. Ni suti ngapi ambazo Kenneth anahitaji kuuza kwa chaguo kuwa sawa?
- Jibu
-
Kenneth angehitaji kuuza suti 1,000.
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua mifumo ya equations kwa kubadilisha.
Dhana muhimu
- Tatua mfumo wa equations kwa kubadilisha
- Kutatua moja ya milinganyo kwa variable ama.
- Badilisha usemi kutoka Hatua ya 1 katika equation nyingine.
- Tatua equation inayosababisha.
- Badilisha ufumbuzi katika Hatua ya 3 katika moja ya milinganyo ya awali ili kupata variable nyingine.
- Andika suluhisho kama jozi iliyoamriwa.
- Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.


